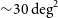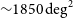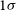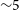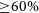1. Introduction
The ability to localise gamma ray bursts (GRBs) from their prompt X-ray/gamma-ray emission is a critical step in the identification and follow-up observation of these cosmic explosions. GRB afterglows are so faint that until the advent of large-aperture, wide-field, deep optical/infrared imaging telescopes (e.g., the Vera Rubin Observatory—albeit with a limited FoV; see LSST Science Collaboration et al. Reference Science Collaboration2017), the location of the burst must be determined purely from its prompt high-energy photon emission.
Accurate GRB localisations and subsequent afterglow follow-up observations are desirable across many areas of astronomy. Observations of long GRB afterglows offer many opportunities to study the high redshift universe and can be used in the study of the cosmic star formation rate (e.g., Robertson & Ellis Reference Robertson and Ellis2012; Trenti, Perna, & Tacchella Reference Trenti, Perna and Tacchella2013; Petrosian, Kitanidis, & Kocevski Reference Petrosian, Kitanidis and Kocevski2015; Chary et al. Reference Chary, Petitjean, Robertson, Trenti and Vangioni2016; Lloyd-Ronning, Aykutalp, & Johnson Reference Lloyd-Ronning, Aykutalp and Johnson2019), investigating the luminosity function of high redshift galaxies (e.g., Trenti et al. Reference Trenti, Perna, Levesque, Shull and Stocke2012; Tanvir et al. Reference Tanvir2012; Salvaterra et al. Reference Salvaterra2012; McGuire Reference McGuire2016), characterising the interstellar medium in distant galaxies (e.g., Klose et al. Reference Klose, Palazzi, Masetti, Stecklum, Greiner, Hartmann and Schmid2004; Berger et al. Reference Berger, Penprase, Fox, Kulkarni, Hill, Schaefer and Reed2005; Vreeswijk et al. Reference Vreeswijk2007; Fox et al. Reference Fox, Ledoux, Vreeswijk, Smette and Jaunsen2008; Prochaska et al. Reference Prochaska, Dessauges–Zavadsky, Ramirez–Ruiz and Chen2008; Thöne et al. Reference Thöne2013; Wiseman et al. Reference Wiseman, Perley, Schady, Prochaska, de Ugarte Postigo, Krühler, Yates and Greiner2017) and measuring the neutral hydrogen fraction along the line of sight (e.g., Miralda Escude Reference Miralda Escude1998; Mesinger & Furlanetto Reference Mesinger and Furlanetto2008; McQuinn et al. Reference McQuinn, Lidz, Zaldarriaga, Hernquist and Dutta2008; Hartoog et al. Reference Hartoog2015; Melandri et al. 2015; Lidz et al. Reference Lidz, Chang, Mas-Ribas and Sun2021).
Furthermore, observations of prompt and afterglow emission from both long and short GRBs provide unique insights into the physics of energy transport and dissipation within relativistic jets (see e.g., Kumar & Zhang Reference Kumar and Zhang2015; Miceli & Nava Reference Miceli and Nava2022 for review articles). For example, the very recent opening of the so-called VHE (Very High Energy) window, with the detection of TeV emission from GRB afterglows (MAGIC Collaboration et al. 2019; Abdalla et al. Reference Abdalla2019; H.E.S.S. Collaboration et al. Reference Collaboration2021), provides us with a new tool to understand the physics of particle acceleration in weakly magnetised ultra-relativistic shocks and may in future also enable a better understanding of highly magnetised mildly relativistic shocks with VHE observations of GRB prompt emission.
More recently, GRB localisations have become useful tools in the field of gravitational wave (GW) science due to the association between short GRBs and compact object mergers (Eichler et al. Reference Eichler, Livio, Piran and Schramm1989; Perna & Belczynski Reference Perna and Belczynski2002; Belczynski et al. Reference Belczynski, Perna, Bulik, Kalogera, Ivanova and Lamb2006). The nearly simultaneous detection of a short GRB within the same localisation region as a GW event provides unique insight into the true nature of these high-energy explosions, as illustrated by the simultaneous observations of the binary neutron star (BNS) coalescence event GW170817, and the short gamma-ray burst GRB170817A (Abbott et al. Reference Abbott2017b) which solidified the link between short GRBs and binary neutron star mergers. In the future, accurate localisations of short GRBs from their high-energy photon emission may also assist in more precise localisation of GW transient events in the case where the uncertainty region from the GW signal is large.
A well-established method to localise high-energy EM transients is triangulation, whereby the source position in the sky is determined by measuring the arrival time difference of light at each detector (see, e.g., Hurley et al. Reference Hurley2013). This method has been used to localise GRBs since they were first discovered by the Vela satellites in 1969 (Klebesadel, Strong, & Olson Reference Klebesadel, Strong and Olson1973) and has been used for the last several decades since 1976 by the Inter-Planetary Network (IPN) (NASA/GSFC Interplanetary Gamma-Ray Burst Timing NetworkFootnote a), an evolving group of independent, separately executed satellite missions all carrying high-energy photon detectors, the data from which can be combined in order to accurately localise GRBs and other high-energy transients (Hurley et al. Reference Hurley, Briggs, Kippen, Kouveliotou, Meegan, Fishman, Cline and Boer1999, Reference Hurley2013, Reference Hurley2017).
Due to the cost-effectiveness of CubeSat technology in achieving specific science goals and the potential benefit to the field of GRB science, many nano-satellite missions and mission concepts are under development to take advantage of this emergent new technology. Such missions include the GRID mission (Wen et al. Reference Wen2019; Wang et al. Reference Wang2021), CAMELOT (Werner et al. Reference Werner2018), GECAM (Zhang et al. Reference Zhang2019), BurstCube (Racusin et al. Reference Racusin2017), EIRSAT-1 (Murphy et al. Reference Murphy2021), and MoonBEAM (Hui & MoonBEAM Team Reference Hui2021). Similarly, small hosted payload instruments on a constellation of larger satellites have been proposed (Greiner et al. Reference Greiner, Hugentobler, Burgess, Berlato, Rott and Tsvetkova2022).
When combined together, all these upcoming instruments for high-energy astrophysics have the potential to significantly contribute to and improve the existing network of GRB satellites within the next decade. In fact, they could establish an all-sky X/gamma-ray monitor capable of high precision localisations and low-latency communications with the ground (given many elements would be in low Earth orbit), which would dramatically increase the number of GRBs identified in near-real time and thus accessible for rapid afterglow follow-up observations.
The HERMES-TP/SP (High-Energy Rapid Modular Ensemble of Satellites—Technologic/Scientific Pathfinder) is a constellation of six 3U nano-satellites (the size of small standardised-form-factor satellites is measured in ‘Units’ U, where 1U
![]() $\approx 10 \times 10 \times 10$
cm
$\approx 10 \times 10 \times 10$
cm
![]() $^3$
), hosting innovative wide field-of-view (FOV) X-ray detectors for the monitoring and localisation of GRBs and high-energy transients (Fiore et al. Reference Fiore2020). Each satellite will be launched into an equatorial low Earth orbit (LEO), and the constellation is designed to not only triangulate GRBs and high-energy transients on the sky (Sanna et al. Reference Sanna2020) but also to probe the quantum structure of spacetime thanks to sub
$^3$
), hosting innovative wide field-of-view (FOV) X-ray detectors for the monitoring and localisation of GRBs and high-energy transients (Fiore et al. Reference Fiore2020). Each satellite will be launched into an equatorial low Earth orbit (LEO), and the constellation is designed to not only triangulate GRBs and high-energy transients on the sky (Sanna et al. Reference Sanna2020) but also to probe the quantum structure of spacetime thanks to sub
![]() $\mu{\rm s}$
timing resolution of the HERMES instrument (Burderi et al. Reference Burderi2020). The HERMES-TP/SP is designed to demonstrate accurate GRB localisation mainly in the right ascension coordinate—the equatorial orbit of the pathfinder satellites imposes inherent geometrical limitations on triangulation which means that GRBs will be only loosely constrained in the declination coordinate (Sanna et al. Reference Sanna2020). This limitation is expected to be addressed in a future HERMES Full Constellation (FC), which is envisioned to consist of tens of satellites into several different orbital planes to achieve accuracy of localising bright long GRBs better than 15′ (Fiore et al. Reference Fiore2020).
$\mu{\rm s}$
timing resolution of the HERMES instrument (Burderi et al. Reference Burderi2020). The HERMES-TP/SP is designed to demonstrate accurate GRB localisation mainly in the right ascension coordinate—the equatorial orbit of the pathfinder satellites imposes inherent geometrical limitations on triangulation which means that GRBs will be only loosely constrained in the declination coordinate (Sanna et al. Reference Sanna2020). This limitation is expected to be addressed in a future HERMES Full Constellation (FC), which is envisioned to consist of tens of satellites into several different orbital planes to achieve accuracy of localising bright long GRBs better than 15′ (Fiore et al. Reference Fiore2020).
As a first step to demonstrate the potential of the HERMES FC, the SpIRIT (Space Industry Responsive Intelligent Thermal) nano-satellite is an Australia-Italy nano-satellite mission planned for launch in 2023 which will operate as part of the HERMES-TP/SP, forming a combined constellation of seven satellites designed to detect and localise high-energy transient events. SpIRIT will be the only satellite among the HERMES Pathfinder to be launched into a Polar orbit, which will enable improved localisation in the declination coordinate due to SpIRIT’s large baseline perpendicular to the equatorial plane. In this capacity, SpIRIT will act as a proof-of-concept for the HERMES FC to demonstrate the GRB localisation capabilities with satellites in different orbital planes.
In this paper we simulate the localisation capabilities of the combined SpIRIT + HERMES-TP/SP constellation in order to understand the improvement gained by having a single satellite element in Polar orbit. As an extension, we further investigate the localisation capabilities of a combined constellation with as many as six additional satellites launched into Polar orbit.
This paper is organised as follows: Section 2 provides a brief background to the HERMES Technologic/Scientific Pathfinder mission and gives details regarding the HERMES X-ray instrument. Section 3 introduces the SpIRIT nano-satellite mission. Section 4 describes our simulation framework and modelling assumptions, as well as the mathematical techniques used for the triangulation and localisation of GRBs. In Section 5 we compare the GRB localisation capabilities and the sky coverage statistics of the HERMES-TP/SP with and without the SpIRIT satellite, and with a larger number of Polar nano-satellites. The main conclusions from this work are presented in Section 6.
2. HERMES-technologic and scientific pathfinder
The HERMES-TP/SP is a constellation of six 3U nano-satellites being developed with funding from the Italian Space Agency and the Italian Ministry for education, University and Research (PI: Burderi) and from the European Union’s Horizon 2020 Research and Innovation Program (PI Fiore; see Fiore et al. Reference Fiore2020 for further details). The HERMES-TP/SP is an in-orbit demonstration of the capabilities of distributed-aperture astronomy in the field of GRB science. It is designed as an intrinsically modular experiment which can later be naturally expanded to provide a global, sensitive all-sky monitor for high-energy transients (the HERMES-FC; see e.g., Fuschino et al. Reference Fuschino2019 for discussion).
The HERMES-TP/SP mission is in advanced stages of development. The critical design review was successfully passed in late 2020 (Fiore et al. Reference Fiore2020), and integration and testing of flight units has been taking place since mid-2021. Integration and testing is continuing throughout 2022, and the constellation is expected to be launched to a nearly equatorial (inclination
![]() $\leq$
$\leq$
![]() $20^{\circ}$
) low Earth orbit (Fiore, Werner, & Behar Reference Fiore, Werner and Behar2021).
$20^{\circ}$
) low Earth orbit (Fiore, Werner, & Behar Reference Fiore, Werner and Behar2021).
Each satellite hosts a miniaturised X-ray detector—the HERMES instrument—based on the so-called ‘siswich’ concept of silicon drift detectors (SDD’s) coupled with scintillator crystals. The instrument has a burst sensitivity of 2 photons cm
![]() $^{-2}$
s
$^{-2}$
s
![]() $^{-1}$
for
$^{-1}$
for
![]() $E \leq 20$
keV and 1 photon cm
$E \leq 20$
keV and 1 photon cm
![]() $^{-2}$
s
$^{-2}$
s
![]() $^{-1}$
for
$^{-1}$
for
![]() $50 \leq E \leq 300$
keV (which is comparable to the Fermi GBM burst sensitivity of
$50 \leq E \leq 300$
keV (which is comparable to the Fermi GBM burst sensitivity of
![]() $<$
$<$
![]() $0.5$
photons cm
$0.5$
photons cm
![]() $^{-2}$
s
$^{-2}$
s
![]() $^{-1}$
between 50 and 300 keV (NASA/GSFC Fermi Gamma-ray Space Telescope GBM Specifications & PerformanceFootnote b)), and low background for its size (Evangelista et al. Reference Evangelista2020; Campana et al. Reference Campana, Fuschino, Evangelista, Dilillo and Fiore2020). Its two operative modes—direct X-ray absorption on the SDD or scintillation light readout from the GAGG crystals—cover a wide energy range (3–60 keV and 20–2 000 keV, respectively; Fuschino et al. Reference Fuschino2020). The instrument has excellent temporal resolution (
$^{-1}$
between 50 and 300 keV (NASA/GSFC Fermi Gamma-ray Space Telescope GBM Specifications & PerformanceFootnote b)), and low background for its size (Evangelista et al. Reference Evangelista2020; Campana et al. Reference Campana, Fuschino, Evangelista, Dilillo and Fiore2020). Its two operative modes—direct X-ray absorption on the SDD or scintillation light readout from the GAGG crystals—cover a wide energy range (3–60 keV and 20–2 000 keV, respectively; Fuschino et al. Reference Fuschino2020). The instrument has excellent temporal resolution (
![]() $<$
400 ns), and has been designed for detection of cosmic high energy transients (such as GRBs) and for the determination of their positions through triangulation via the distributed detector architecture.
$<$
400 ns), and has been designed for detection of cosmic high energy transients (such as GRBs) and for the determination of their positions through triangulation via the distributed detector architecture.
The response function of the HERMES instrument depends on both the energy of the incoming photon and its incident angle on the detector relative to the line of sight (LOS), and we refer to Campana et al. (Reference Campana, Fuschino, Evangelista, Dilillo and Fiore2020) for a plot of the instrument response as a function of photon energy and incident angle. The response of the HERMES instrument as a function of incident angle for energies between 50 and 300 keV can be approximated by a cosine profile with respect to the LOS, meaning that the full width at half maximum (FWHM) of the instrument is 120 deg, corresponding to an effective FOV of 3.2sr FWHM or, equivalently, a circular FOV with a radius
![]() $60^{\circ}$
(Colagrossi et al. Reference Colagrossi, Prinetto, Silvestrini and Lavagna2020; Evangelista et al. Reference Evangelista2020). In this work we adopt the use of a cosine profile out to a radius of 80 degrees for the instrument response (IR):
$60^{\circ}$
(Colagrossi et al. Reference Colagrossi, Prinetto, Silvestrini and Lavagna2020; Evangelista et al. Reference Evangelista2020). In this work we adopt the use of a cosine profile out to a radius of 80 degrees for the instrument response (IR):
The 80 degree cutoff is motivated as approximately representative of the physical obstructions to the detector field of view, given how the instrument is mounted on the SpIRIT satellite. We note that we have assumed that the aluminium chassis of the satellite and the tungsten shielding of the instrument block all radiation coming from incident angles
![]() $>$
$>$
![]() $80^{\circ}$
—in reality this may not be the case, and a more detailed procedure—or ultimately in-orbit verification against GRBs with known localisation—would be needed to determine which satellites observe the GRB within their FOV and which observe it off-axis. In the context of this work, the approximation given in Equation (1) is sufficient for quantifying the improvement in GRB localisations gained by augmenting the HERMES-TP/SP with satellites in Polar orbit.
$80^{\circ}$
—in reality this may not be the case, and a more detailed procedure—or ultimately in-orbit verification against GRBs with known localisation—would be needed to determine which satellites observe the GRB within their FOV and which observe it off-axis. In the context of this work, the approximation given in Equation (1) is sufficient for quantifying the improvement in GRB localisations gained by augmenting the HERMES-TP/SP with satellites in Polar orbit.
3. SpIRIT nano-satellite
The SpIRIT satellite is an Australia-Italy mission supported in Australia by the Australian Space Agency International Space Investment—Expand Capability scheme. SpIRIT is a 6U CubeSat with
![]() ${\sim}$
${\sim}$
![]() $11.5\,\mathrm{kg}$
mass and linear dimensions of approximately
$11.5\,\mathrm{kg}$
mass and linear dimensions of approximately
![]() $30\times 20 \times 10\,\mathrm{cm}$
when stowed in the launch dispenser. SpIRIT will be launched in a Polar Sun-synchronous orbit with
$30\times 20 \times 10\,\mathrm{cm}$
when stowed in the launch dispenser. SpIRIT will be launched in a Polar Sun-synchronous orbit with
![]() ${\sim}$
${\sim}$
![]() $550\,\mathrm{km}$
altitude and approximately 1:30pm LTDN (Local Time at the Descending Node) and has a target main mission lifetime of 24 months including commissioning.
$550\,\mathrm{km}$
altitude and approximately 1:30pm LTDN (Local Time at the Descending Node) and has a target main mission lifetime of 24 months including commissioning.
SpIRIT is being developed by an Australian consortium led by the University of Melbourne (PI: Michele Trenti), which is responsible for the project management and mission design, as well as for the development of four subsystems:
-
1. The Payload Management System (PMS), a dedicated computer that manages operations of all payloads and related data processing. This system is based on a SmartFusion2 System on Chip (SoC) Field Programmable Gate Array (FPGA) which includes a Cortex-M3 microprocessor and FPGA logic. A Graphic Processing Unit is also part of PMS for additional on-board data processing capabilities (including a progressive compression algorithm for improved performance in imaging data downlink). PMS also includes a Power Management Module with multiple supercapacitors to guarantee up to 60 s of uninterrupted power supply to the HERMES instrument and allow it to transition to a safe mode in case of temporary power failure at the platform level.
-
2. The Thermal Management Integrated System (TheMIS), a subsystem for precision thermal management and active cooling of payloads that includes (a) a Stirling cycle cryocooler capable of achieving
 $T=80\,\mathrm{K}$
cold-tip temperature, (b) custom-developed control electronics designed for space operations, (c) multiple temperature monitoring sensors, (d) and deployable thermal radiators.
$T=80\,\mathrm{K}$
cold-tip temperature, (b) custom-developed control electronics designed for space operations, (c) multiple temperature monitoring sensors, (d) and deployable thermal radiators. -
3. Mercury, a low-latency communication subsystem that combines Iridium and Globalstar user terminals to provide capability of sending and receiving short burst data packets (e.g. target of opportunity commands or burst alerts).
-
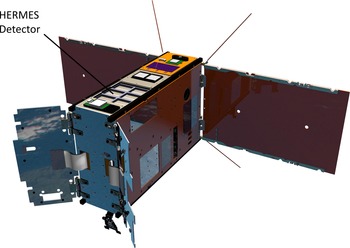
4. LORIS, a set of visible and near-infrared inspection cameras that will monitor and characterise key elements of the spacecraft, including one mounted on a deployable arm, seen on the bottom of the satellite in Figure 1.

Figure 1. Diagram of the SpIRIT nano-satellite, demonstrating the orientation of the solar panels (facing away from the view on the right) relative to the HERMES instrument (located on the top face near the left). Also visible on the left side are the deployable thermal radiators.
The main scientific payload of SpIRIT is a HERMES instrument unit, identical to the ones that will fly on the HERMES-TP/SP satellites. The HERMES instrument on SpIRIT will accumulate a higher total ionising dose compared to a satellite in an equatorial orbit due to its repeated passage over the South Atlantic Anomaly and the Poles. To reduce the resultant buildup of leakage current and mitigate the performance degradation of the instrument (Dilillo et al. Reference Dilillo2020), SpIRIT will feature active thermal management conducted by the TheMIS payload, with a target operating temperature of
![]() $T=245\pm1\,\mathrm{K}$
. The lower the temperature the greater the benefit, and TheMIS would, in principle, be capable of cooling a well-insulated instrument to cryogenic temperatures (
$T=245\pm1\,\mathrm{K}$
. The lower the temperature the greater the benefit, and TheMIS would, in principle, be capable of cooling a well-insulated instrument to cryogenic temperatures (
![]() $T\sim 80\,\mathrm{K}$
), but the HERMES instrument electronics in the current design are only rated to
$T\sim 80\,\mathrm{K}$
), but the HERMES instrument electronics in the current design are only rated to
![]() $T\gtrsim 240\,\mathrm{K}$
. A CAD illustration of the satellite is shown in Figure 1.
$T\gtrsim 240\,\mathrm{K}$
. A CAD illustration of the satellite is shown in Figure 1.
All of these elements make SpIRIT a mission designed to demonstrate new technologies in orbit and the scientific operation and performance of the HERMES instrument in high inclination orbits.
4. Simulating GRB triangulation
In this section, we introduce our analysis framework to simulate and localise GRBs using the HERMES (+ SpIRIT) nano-satellite constellation.
4.1. Satellite orbits
Using as a starting point of our analysis the orbital configuration and pointing strategy presented in Colagrossi et al. (Reference Colagrossi, Prinetto, Silvestrini and Lavagna2020), we simulate each of the six satellites in the HERMES-TP/SP as being uniformly spaced around the same circular 550 km equatorial orbit (
![]() $\text{inclination} = 0$
,
$\text{inclination} = 0$
,
![]() $\text{eccentricity} = 0$
).
$\text{eccentricity} = 0$
).
For simplicity we presume that the satellites maintain their equidistant spacing over time, neglecting environmental perturbations to each spacecraft’s orbit. We note that this configuration is close to the optimal configuration of the HERMES-TP/SP as it maintains a large baseline between neighbouring satellites, meaning that our results will show an idealised comparison between the HERMES-TP/SP and SpIRIT + HERMES-TP/SP constellations.
We model the SpIRIT satellite in a 550 km Polar sun-synchronous circular orbit (
![]() $\text{inclination} = 97.6^{\circ}$
,
$\text{inclination} = 97.6^{\circ}$
,
![]() $\text{eccentricity} = 0$
) with a 1:30pm LTDN. When modelling several SpIRIT-like satellites in Polar orbit, we position them equally around a 550 km Polar sun-synchronous orbit, just as the HERMES-TP/SP is uniformly spaced around an equatorial orbit. The spacing of the satellites around a Polar orbit depends on how many satellites are in this orbital plane, e.g., two satellites in Polar orbit will be on opposite sides of the globe, but four satellites will only be a quarter of the way around the globe from their nearest neighbour.
$\text{eccentricity} = 0$
) with a 1:30pm LTDN. When modelling several SpIRIT-like satellites in Polar orbit, we position them equally around a 550 km Polar sun-synchronous orbit, just as the HERMES-TP/SP is uniformly spaced around an equatorial orbit. The spacing of the satellites around a Polar orbit depends on how many satellites are in this orbital plane, e.g., two satellites in Polar orbit will be on opposite sides of the globe, but four satellites will only be a quarter of the way around the globe from their nearest neighbour.
4.2. Particle background modelling
The scientific operations of the HERMES and SpIRIT satellites are highly dependent on the high-energy particle flux in low-Earth orbit. Space radiation can not only damage the solid-state sensors (Ripa et al. Reference Ripa, Dilillo, Campana and Galgoczi2020), but it also increases the level of background noise in the HERMES instrument (Dilillo et al. Reference Dilillo2020, Reference Dilillo2022), making it more difficult to detect faint GRBs and increasing the signal cross-correlation uncertainty when trying to triangulate a burst. While the influence of high-energy particles is minimal for satellites in low-altitude equatorial orbit, they will have a substantial impact on SpIRIT which—due to its Polar orbit—will traverse multiple times a day both of the high flux regions around the poles as well as the South Atlantic Anomaly (SAA). While there is still a background flux of particles outside of the SAA and the poles (see e.g., Ling Reference Ling1975; Cumani et al. Reference Cumani, Hernanz, Kiener, Tatischeff and Zoglauer2019), the flux is low enough that it does not prohibit the detection of GRBs or pose a risk to the operation of the detector.
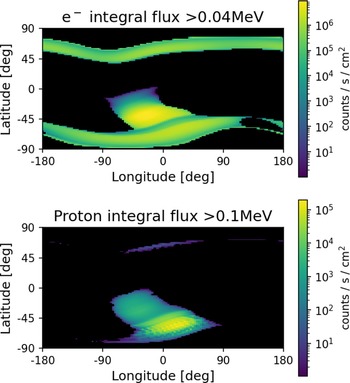
In this work we make use of particle background maps from ESA’s Space Environment Information SystemFootnote c (SPENVIS), specifically the time-averaged electron integral flux above 0.04 MeV and the proton integral flux above 0.1 MeV obtained using the AP8MIN and AE8MAX models included in SPENVIS (Figure 2). Conservatively, we assume that SpIRIT and the HERMES satellites will not operate the HERMES instrument while travelling through a region with non-zero particle background in the maps considered (non-black regions in Figure 2), and we take this into account in the orbital simulations presented in Section 4.4. With this assumption, and taking into account the orbits defined in Section 4.1, we find that on average each satellite in the HERMES-TP/SP has approximately a
![]() ${\sim}$
92% duty cycle, while SpIRIT (and any satellite in Polar orbit) has a
${\sim}$
92% duty cycle, while SpIRIT (and any satellite in Polar orbit) has a
![]() ${\sim}$
65% duty cycle.
${\sim}$
65% duty cycle.

Figure 2. Particle background maps (in Earth coordinates) for a satellite in 550 km low Earth orbit, obtained using the AP8MIN (protons) and AE8MAX (electrons) models included in ESA’s SPENVIS system. Note that the South Atlantic Anomaly (the high particle flux region around lat
![]() ${\sim}{-}45$
, lon
${\sim}{-}45$
, lon
![]() ${\sim} 0$
) features in both the electron and proton flux maps. The high-flux bars across the top and bottom of the e
${\sim} 0$
) features in both the electron and proton flux maps. The high-flux bars across the top and bottom of the e
![]() $^-$
map reflect the rings around Earth’s poles. In the colour scheme, black indicates regions with zero integral flux.
$^-$
map reflect the rings around Earth’s poles. In the colour scheme, black indicates regions with zero integral flux.
As a consistency check for the duty cycle and particle background modelling, we considered in-flight data from VZLUSAT-2 (Granja et al. Reference Granja2022) (mission overview available online at the VZLUSAT-2 websiteFootnote d) and GRBAlpha (Pál et al. Reference Pál2020), two satellites that carry a similar detector to the HERMES instrument. Here we computed the fraction of their orbits where the instrument noise is below the threshold to detect a typical long GRB at
![]() $S/N>5$
(i.e. assuming a GRB flux greater than
$S/N>5$
(i.e. assuming a GRB flux greater than
![]() $1.19\,\mathrm{ph\,cm}$
$1.19\,\mathrm{ph\,cm}$
![]() $^{-2}$
s
$^{-2}$
s
![]() $^{-1}$
for energy
$^{-1}$
for energy
![]() $E>30\,\mathrm{keV}$
) using the simulation framework outlined in Galgóczi et al. (Reference Galgóczi2021). After mapping those results to the expected orbit of SpIRIT (taking advantage of the similarity with VZLUSAT-2, which is also in a Polar orbit, and rescaling for the sensitivity of HERMES) we estimate a 67% duty cycle for SpIRIT, which is in very good agreement with the estimate derived using the particle background maps.
$E>30\,\mathrm{keV}$
) using the simulation framework outlined in Galgóczi et al. (Reference Galgóczi2021). After mapping those results to the expected orbit of SpIRIT (taking advantage of the similarity with VZLUSAT-2, which is also in a Polar orbit, and rescaling for the sensitivity of HERMES) we estimate a 67% duty cycle for SpIRIT, which is in very good agreement with the estimate derived using the particle background maps.
4.3. Satellite pointing strategy
The pointing direction of SpIRIT is constrained by several factors. The first constraint is the requirement to keep its solar panels illuminated by the Sun (i.e. within
![]() $\pm 20^{\circ}$
of the Sun normal vector), which in turn restricts the direction that the on board HERMES detector—located on a face orthogonal to the solar panel—can point at, since the solar panels are fixed (see Figure 1). Secondly, it is undesirable to point the HERMES instrument within a
$\pm 20^{\circ}$
of the Sun normal vector), which in turn restricts the direction that the on board HERMES detector—located on a face orthogonal to the solar panel—can point at, since the solar panels are fixed (see Figure 1). Secondly, it is undesirable to point the HERMES instrument within a
![]() $90^{\circ}$
angle of the Sun, as this would cause the detector to be directly illuminated by sunlight. The final constraint that we impose on SpIRIT’s pointing in this work is the requirement to align its field of view with that of the HERMES-TP/SP to ensure the concurrent detection of GRB events.
$90^{\circ}$
angle of the Sun, as this would cause the detector to be directly illuminated by sunlight. The final constraint that we impose on SpIRIT’s pointing in this work is the requirement to align its field of view with that of the HERMES-TP/SP to ensure the concurrent detection of GRB events.
A full optimisation of the pointing strategy of a nano-satellite constellation which combines satellites in equatorial and Polar orbits with additional astrophysical constraints (i.e. preference for avoidance of the galactic plane) is beyond the scope of this work. Instead, we adopt a simplified framework (Figure 3) taking advantage of the pointing strategy optimisation already carried out by the HERMES-TP/SP team (Colagrossi et al. Reference Colagrossi, Prinetto, Silvestrini and Lavagna2020; Sanna et al. Reference Sanna2020):
-
The six satellites in the HERMES-TP/SP follow the optimal pointing strategy outlined in Sanna et al. (Reference Sanna2020), where the constellation is arranged into two co-pointing groups of three satellites. In this work we orient those two co-pointing groups at right angles to the sun, towards the coordinates
 $(\alpha, \delta) = (\alpha_{\text{sun}} + 90^{\circ}, 0^{\circ})$
or
$(\alpha, \delta) = (\alpha_{\text{sun}} + 90^{\circ}, 0^{\circ})$
or
 $(\alpha_{\text{sun}}-90^{\circ},0^{\circ})$
. While the satellites orbit around the globe they will re-orient themselves to point at whichever field of view is not obstructed by the Earth. This results in both pointing directions being constantly observed by three HERMES-TP/SP satellites at any given time.
$(\alpha_{\text{sun}}-90^{\circ},0^{\circ})$
. While the satellites orbit around the globe they will re-orient themselves to point at whichever field of view is not obstructed by the Earth. This results in both pointing directions being constantly observed by three HERMES-TP/SP satellites at any given time. -
The SPIRIT nano-satellite will align its field of view with one of the HERMES-TP/SP triplets at any given point in time, pointing at either
 $(\alpha, \delta) = (\alpha_{\text{sun}} + 90^{\circ}, 0^{\circ})$
or
$(\alpha, \delta) = (\alpha_{\text{sun}} + 90^{\circ}, 0^{\circ})$
or
 $(\alpha_{\text{sun}}-90^{\circ},0^{\circ})$
. As SpIRIT crosses the Earth’s poles, it will re-orient itself to point in the opposite direction such that its field of view is always minimally obstructed by Earth. In the case of additional Polar satellites similar to SpIRIT, each satellite will independently follow this strategy such that every satellite is co-pointing with one of the HERMES-TP/SP triplets at any given point in time.
$(\alpha_{\text{sun}}-90^{\circ},0^{\circ})$
. As SpIRIT crosses the Earth’s poles, it will re-orient itself to point in the opposite direction such that its field of view is always minimally obstructed by Earth. In the case of additional Polar satellites similar to SpIRIT, each satellite will independently follow this strategy such that every satellite is co-pointing with one of the HERMES-TP/SP triplets at any given point in time.
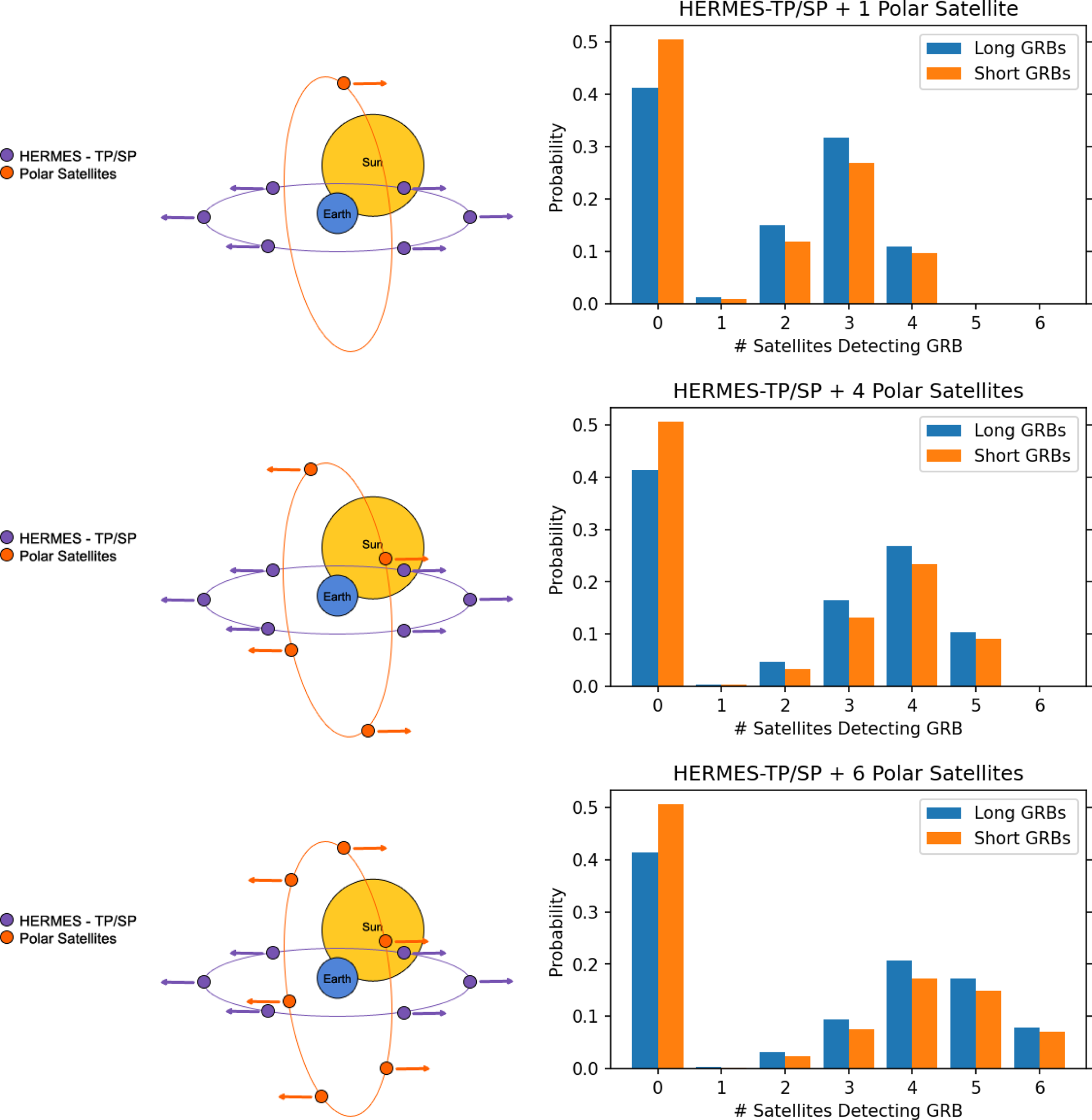
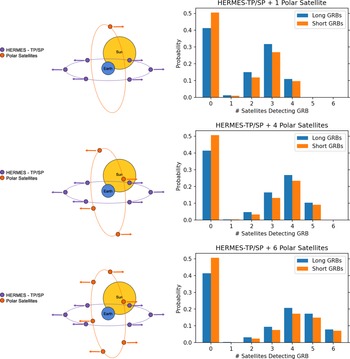
Figure 3.
Left column: 3D representation of the pointing strategy of the combined SpIRIT + HERMES-TP/SP constellation (not to scale). Note that for each constellation the satellites in a given orbital plane are uniformly spaced around their orbit. Note that for a satellite with n elements in Polar orbit, the maximum number of Polar-orbiting satellites which can simultaneously detect a GRB is
![]() $n/2$
(with the exception of the case of a single Polar satellite). Right column: Sky-coverage analysis of the corresponding constellation demonstrating the probability that a random GRB will be detected by n satellites (taking into account satellite FOV, the nominal flux limit of the HERMES instrument, and satellite passage through regions of high particle flux) generated from
$n/2$
(with the exception of the case of a single Polar satellite). Right column: Sky-coverage analysis of the corresponding constellation demonstrating the probability that a random GRB will be detected by n satellites (taking into account satellite FOV, the nominal flux limit of the HERMES instrument, and satellite passage through regions of high particle flux) generated from
![]() $10^4$
simulated trials.
$10^4$
simulated trials.
Note that for the actual HERMES-TP/SP constellation in orbit (or for any constellation of Polar-orbiting satellites) the satellites will drift over time in absence of active orbital control manoeuvre, hence the pointing strategy of the satellite triplets would have to be constantly updated and optimised based on the actual positions of the satellites (Sanna et al. Reference Sanna2020). However, in this work we neglect satellite drift, using instead the simplified configuration with constant relative orbital phases as outlined above.
4.4. Simulation method
We model the orbits of each satellite as defined in Section 4.1. We ignore the Moon in our simulations since it occupies such a small fraction (
![]() ${\sim}$
${\sim}$
![]() $0.25^{\circ}$
radius) of the sky, and likewise the influence of the Sun is not relevant as our satellites point at a
$0.25^{\circ}$
radius) of the sky, and likewise the influence of the Sun is not relevant as our satellites point at a
![]() $90^{\circ}$
offset from the Sun and their FoV only has a
$90^{\circ}$
offset from the Sun and their FoV only has a
![]() $80^{\circ}$
radius. However, we do track the position of Earth for LoS obstruction calculations; from a 550 km LEO, Earth has an angular diameter of
$80^{\circ}$
radius. However, we do track the position of Earth for LoS obstruction calculations; from a 550 km LEO, Earth has an angular diameter of
![]() ${\sim}$
${\sim}$
![]() $134^{\circ}$
, meaning that Earth will maximally encroach on one side of the satellite’s FOV by
$134^{\circ}$
, meaning that Earth will maximally encroach on one side of the satellite’s FOV by
![]() ${\sim}$
${\sim}$
![]() $47^{\circ}$
when Earth is perpendicular to the satellite’s pointing direction (assuming the HERMES instrument’s FOV has a radius of
$47^{\circ}$
when Earth is perpendicular to the satellite’s pointing direction (assuming the HERMES instrument’s FOV has a radius of
![]() $80^{\circ}$
). We additionally track the operational status of the HERMES instrument on board each satellite based on the particle background maps presented in Section 4.2.
$80^{\circ}$
). We additionally track the operational status of the HERMES instrument on board each satellite based on the particle background maps presented in Section 4.2.
To compare the localisation capabilities of different sized nano-satellite constellations, we generate a random sample of
![]() $10^4$
long and
$10^4$
long and
![]() $10^4$
short GRB events for each constellation that we test. The procedure for simulating each GRB is as follows:
$10^4$
short GRB events for each constellation that we test. The procedure for simulating each GRB is as follows:
-
1. Each GRB is generated with a random right ascension and declination (sampled from a uniform distribution across the celestial sphere), and occurs at a random time in the year.
-
2. We generate the flux,
 $F_{GRB}$
, of the GRB by selecting a random burst from the Fermi GBM catalog (FERMIGBRST—Fermi GBM Burst CatalogFootnote e; von Kienlin et al. Reference von Kienlin2020; Gruber et al. Reference Gruber2014; von Kienlin et al. Reference von Kienlin2014; Bhat et al. Reference Bhat2016). Specifically, we randomly select one of the ‘Flnc_Band_Phtfluxb’ values (the average photon flux, in photon/cm2/s between 50 and 300 keV, for a Band function law fit to a single spectrum over the duration of the burst. For long GRBs, we sample from the set of bursts with
$F_{GRB}$
, of the GRB by selecting a random burst from the Fermi GBM catalog (FERMIGBRST—Fermi GBM Burst CatalogFootnote e; von Kienlin et al. Reference von Kienlin2020; Gruber et al. Reference Gruber2014; von Kienlin et al. Reference von Kienlin2014; Bhat et al. Reference Bhat2016). Specifically, we randomly select one of the ‘Flnc_Band_Phtfluxb’ values (the average photon flux, in photon/cm2/s between 50 and 300 keV, for a Band function law fit to a single spectrum over the duration of the burst. For long GRBs, we sample from the set of bursts with
 $T90> 2$
s (as reported by the catalogue), and for short GRBs we take those with
$T90> 2$
s (as reported by the catalogue), and for short GRBs we take those with
 $T90 \lt 2$
s, where T90 is defined as the time interval over which the GRB emits 90% of the total energy of its prompt emission phase.
$T90 \lt 2$
s, where T90 is defined as the time interval over which the GRB emits 90% of the total energy of its prompt emission phase. -
3. If the GRB occurs within the FOV of one of the co-pointing groups in the constellation, we check whether each satellite has LOS to the coordinates of the GRB or whether they are occulted by the Earth.
For each satellite that has LOS to the burst we calculate the observed GRB flux,
 $F_{obs}$
, based on the incident angle of the GRB to the detector (Equation (1)). Note that we do not include Poisson noise on the observed flux of the GRB.
$F_{obs}$
, based on the incident angle of the GRB to the detector (Equation (1)). Note that we do not include Poisson noise on the observed flux of the GRB.We model the flux sensitivity of the HERMES instrument as four times less sensitive than Fermi GBM (as per Section 2). Given we are sampling ‘Flnc_Band_Phtfluxb’ values from the Fermi GBM database, this corresponds to:
(2) \begin{equation} F_{\text{lim}} = \begin{cases} 0.463\text{ph}\,\text{cm}^{-2}\,{\rm s^{-1}} , \quad\text{Long GRBs} \\[4pt] 1.861\text{ph}\,\text{cm}^{-2}\,{\rm s^{-1}} , \quad \text{Short GRBs} \end{cases} \end{equation}
\begin{equation} F_{\text{lim}} = \begin{cases} 0.463\text{ph}\,\text{cm}^{-2}\,{\rm s^{-1}} , \quad\text{Long GRBs} \\[4pt] 1.861\text{ph}\,\text{cm}^{-2}\,{\rm s^{-1}} , \quad \text{Short GRBs} \end{cases} \end{equation}
We consider a satellite to detect a GRB if it has LOS to the burst and
 $F_{\text{obs}} \gt F_{\text{lim}}$
.
$F_{\text{obs}} \gt F_{\text{lim}}$
.Note that in the simplified context of our simulation the value of
 $F_{\rm obs}$
is the same for all co-pointing satellites in the constellation, since we model them as pointing at the exact same coordinates. In reality this issue is far more complex—the pointing of each satellite will drift slightly, the response function of each HERMES instrument may differ slightly in shape or absolute value, and there will be incident angle-dependent energy dispersion which scatters high-energy photons down to lower energies, influencing the number of photons in the chosen energy band.
$F_{\rm obs}$
is the same for all co-pointing satellites in the constellation, since we model them as pointing at the exact same coordinates. In reality this issue is far more complex—the pointing of each satellite will drift slightly, the response function of each HERMES instrument may differ slightly in shape or absolute value, and there will be incident angle-dependent energy dispersion which scatters high-energy photons down to lower energies, influencing the number of photons in the chosen energy band. -
4. We compute the standard deviation on cross-correlation uncertainty
 $\sigma_{cc}$
according to the observed flux
$\sigma_{cc}$
according to the observed flux
 $F_{obs}$
using the power-law fits plus Gaussian scatter model detailed in Table 1.
$F_{obs}$
using the power-law fits plus Gaussian scatter model detailed in Table 1.
We note that this method contains several large simplifications regarding the photon energy, noise treatment, and incident angle response of the HERMES instrument and the relation between GRB flux and cross-correlation uncertainty, both of which will impact the accuracy of the results presented in this work. However, as the purpose of this work is to demonstrate the improved localisation performance gained by launching a satellite into a different orbital plane, we proceed with these simplifying assumptions and highlight that our results should only be considered an approximate estimate of the nano-satellite constellation’s GRB localisation capabilities to within a factor
![]() $\approx 2$
of precision.
$\approx 2$
of precision.
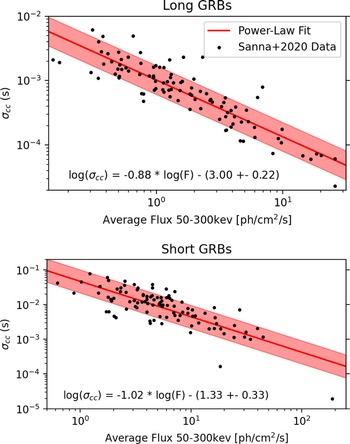
Table 1. Power-law fits to the data presented in Sanna et al. (Reference Sanna2020) used to calculate the uncertainty in signal arrival-time from the average flux of the GRB between 50 and 300 kev.

4.4.1. Subsample of ‘observable’ GRBs
By construction, the method presented above includes the generation of GRB events that cannot be observed by the nano-satellite constellation (either because they are too faint or occur outside the FOV of the constellation), or that are otherwise unsuitable for localisation if too few satellites detect the burst. For these reasons, and to aid in the clarity of our results, we define the following additional conditions that must be met in order to include a GRB in our sample of
![]() $10^4$
events that we use as base for our analysis:
$10^4$
events that we use as base for our analysis:
-
The GRB must occur within the FOV of one of the co-pointing groups in the constellation:
 \begin{equation*} \text{Burst incident angle } \unicode{x03B8} \leq 80^{\circ}. \end{equation*}
\begin{equation*} \text{Burst incident angle } \unicode{x03B8} \leq 80^{\circ}. \end{equation*}
Since the nano-satellite constellation is divided into two co-pointing groups each pointing in opposite directions the burst can only ever be detected by one co-pointing group at a time.
-
The observed flux of the GRB must be higher than the nominal flux limit of the HERMES instrument:
 \begin{equation*} F_{\text{obs}} = F_{\text{GRB}} \times \cos{\unicode{x03B8} } \geq F_{\text{lim}}. \end{equation*}
\begin{equation*} F_{\text{obs}} = F_{\text{GRB}} \times \cos{\unicode{x03B8} } \geq F_{\text{lim}}. \end{equation*}
-
At least three satellites in the constellation must directly detect the burst:
 \begin{equation*} N_{\text{det}} \geq 3. \end{equation*}
\begin{equation*} N_{\text{det}} \geq 3. \end{equation*}
In order to localise the burst using triangulation techniques at least three independent detections are needed (see Section 4.5). Note that we do not enforce that every satellite in the co-pointing group detects the GRB, since Earth may reduce the effective field of view of some elements, and a non-detection in this context can still contribute to the burst localisation (see Section 4.5.3 for further discussion).
-
Every satellite in the co-pointing group must be operational at the time of the burst (i.e., not travelling through a region of high particle flux). We impose this restriction because the GRB localisation capabilities of an n-satellite constellation with one satellite missing are approximately equivalent to localisation statistics reported by an (n-1) satellite constellation (not taking into account the FOV and orbital position of each satellite). Therefore, to avoid such overlap in our results we enforce that every co-pointing satellite is operational at the time of the burst.
-
In the case of the SpIRIT + HERMES-TP/SP constellation (i.e., a constellation with only one satellite in Polar orbit) we impose one additional condition that SpIRIT is part of the co-pointing group that detects the GRB. Without this condition, the localisation capabilities presented for the SpIRIT + HERMES-TP/SP constellation would consist both of bursts that are observed by SpIRIT + 3 HERMES satellites, as well as bursts that are observed by only 3 HERMES satellites, the latter of which would be identical to the localisation capabilities presented for the HERMES-TP/SP constellation alone. Therefore we ensure that SpIRIT is part of the co-pointing group that detects the GRB, which is only true for
 ${\sim}$
50% of bursts (since SpIRIT can only point towards one of the two fields at any given time). Note that we do not enforce that SpIRIT detects the GRB; we only impose that it is co-pointing with other satellites that detect the GRB.
${\sim}$
50% of bursts (since SpIRIT can only point towards one of the two fields at any given time). Note that we do not enforce that SpIRIT detects the GRB; we only impose that it is co-pointing with other satellites that detect the GRB.
If a simulated GRB meets these conditions, then we include it in our sample and perform the localisation technique described in the following section.
4.5. Triangulating GRBs
4.5.1. Triangulation method
In this work we follow the localisation method used in Sanna et al. (Reference Sanna2020), which utilises the arrival time difference of photons at each detector in order to triangulate the position of the GRB. This technique has been used for decades by the IPN to triangulate the positions of GRBs (see e.g., Hurley et al. Reference Hurley, Briggs, Kippen, Kouveliotou, Meegan, Fishman, Cline and Boer1999, Reference Hurley2013), and as such is appropriate for our estimation purposes, despite some limitations discussed more in Section 4.5.2. Here, we provide a brief outline of the method, referring the reader to the work referenced above for full details.
As GRBs occur at cosmological distances, one can represent the gamma ray photons from the burst as a narrow plane wave travelling through space. Given a network of n detectors distributed throughout space (i.e., a satellite constellation), this plane wave will pass over each detector i at a different global time
![]() $t_i$
depending on the coordinates of each detector
$t_i$
depending on the coordinates of each detector
![]() $\vec{r}_i$
.
$\vec{r}_i$
.
If the GRB occurred at right ascension
![]() $\alpha$
and declination
$\alpha$
and declination
![]() $\delta$
, its Cartesian direction can be represented by unit vector
$\delta$
, its Cartesian direction can be represented by unit vector
![]() $\hat d$
:
$\hat d$
:
Defining
![]() $t_0$
as the time the GRB signal reaches the origin of the chosen reference frame, the arrival time of photons at detector i is then given by
$t_0$
as the time the GRB signal reaches the origin of the chosen reference frame, the arrival time of photons at detector i is then given by
Where
![]() $\vec{r_i}$
represents the position vector of the i-th detector. The time delay between two satellites will then be:
$\vec{r_i}$
represents the position vector of the i-th detector. The time delay between two satellites will then be:
In Equation (5),
![]() $\Delta t_{ij}$
represents the difference in arrival time of the signal at each instrument due purely to satellite geometry. The measured value of time delay
$\Delta t_{ij}$
represents the difference in arrival time of the signal at each instrument due purely to satellite geometry. The measured value of time delay
![]() $\Delta \tau_{ij}$
will depend on this intrinsic time delay plus some offset due to measurement uncertainty:
$\Delta \tau_{ij}$
will depend on this intrinsic time delay plus some offset due to measurement uncertainty:
where the term
![]() $\mathcal{N}(0,\sigma_{cc})$
represents the uncertainty on the measurement of the arrival time difference. This timing uncertainty is discussed in detail in Sections 4.5.2 and 4.5.3.
$\mathcal{N}(0,\sigma_{cc})$
represents the uncertainty on the measurement of the arrival time difference. This timing uncertainty is discussed in detail in Sections 4.5.2 and 4.5.3.
To estimate the true position of the GRB, we compare the measured time delay pairs
![]() $\Delta \tau_{ij}(\hat d_{GRB})$
from each satellite that detected the GRB to the time delays that would be measured if the GRB were coming from some guess direction,
$\Delta \tau_{ij}(\hat d_{GRB})$
from each satellite that detected the GRB to the time delays that would be measured if the GRB were coming from some guess direction,
![]() $\Delta t_{ij}\left(\hat d_{guess}\right)$
. In this work we perform this comparison using a non-linear least squares method: we define the
$\Delta t_{ij}\left(\hat d_{guess}\right)$
. In this work we perform this comparison using a non-linear least squares method: we define the
![]() $\chi^2\left(\hat d_{guess}\right)$
function as the sum of the squares of the differences between the expected and measured time delays divided by the uncertainty on the signal alignment after cross-correlation:
$\chi^2\left(\hat d_{guess}\right)$
function as the sum of the squares of the differences between the expected and measured time delays divided by the uncertainty on the signal alignment after cross-correlation:
 \begin{equation} \chi^2\left(\hat d_{guess}\right) = \sum_{i=0}^{n-2}\sum_{j=i+1}^{n-1} \frac{\left(\Delta \tau_{ij}\left(\hat d_{GRB}\right)\right. - \Delta t_{ij}\left(\hat d_{guess}\right)^2}{\sigma_{\text{cc}}^2}. \end{equation}
\begin{equation} \chi^2\left(\hat d_{guess}\right) = \sum_{i=0}^{n-2}\sum_{j=i+1}^{n-1} \frac{\left(\Delta \tau_{ij}\left(\hat d_{GRB}\right)\right. - \Delta t_{ij}\left(\hat d_{guess}\right)^2}{\sigma_{\text{cc}}^2}. \end{equation}
The coordinates of the GRB can then be estimated by finding the value of
![]() $\hat d_{guess}$
which minimise the
$\hat d_{guess}$
which minimise the
![]() $\chi^2$
function. Equation (7) takes the form of a ‘minimum
$\chi^2$
function. Equation (7) takes the form of a ‘minimum
![]() $\chi^2$
’ function with two degrees of freedom (right ascension and declination), and so we estimate the 68% and 90% confidence region of the source localisation as the set of all values of
$\chi^2$
’ function with two degrees of freedom (right ascension and declination), and so we estimate the 68% and 90% confidence region of the source localisation as the set of all values of
![]() $\alpha, \delta$
where (Avni Reference Avni1976):
$\alpha, \delta$
where (Avni Reference Avni1976):
Note that Equation (8) is a linear approximation for determining the 68% and 90% confidence intervals. In fact this equation is only asymptotically correct for linear models, and as triangulation is a non-linear problem, the degrees of freedom are not necessarily exactly 2. In fact, the exact value of the degrees of freedom depends on data quality and predictiveness of the fit parameters (e.g., Janson, Fithian, & Hastie Reference Hurley2013).
Finally, we consider the sky coverage and LOS of each satellite in the co-pointing group, which influences GRB localisation depending on whether each satellite directly detects the GRB:
-
If a satellite detects the GRB, we exclude all directions
 $\hat d_{guess}$
from the localisation region that are either outside that satellites FOV or obstructed by the Earth from that satellite’s perspective.
$\hat d_{guess}$
from the localisation region that are either outside that satellites FOV or obstructed by the Earth from that satellite’s perspective. -
If one satellite in a co-pointing group does not detect the GRB, but other satellites in that co-pointing group detect the burst, then we only consider possible burst directions
 $\hat d_{guess}$
that were obstructed by Earth from the non-detecting satellite’s perspective.
$\hat d_{guess}$
that were obstructed by Earth from the non-detecting satellite’s perspective.
4.5.2. Signal cross-correlation uncertainty
The triangulation method for GRB localisation relies heavily on an accurate estimation of
![]() $\Delta \tau_{ij}$
—the measured time difference between the signal arriving at each detector in the network. Classically, this time difference has been computed by binning the light curves observed by each detector with some temporal resolution (which usually depends on the flux of the GRB—brighter bursts can be binned with finer resolution), and then using a cross-correlation algorithm to determine the time offset between the two observed signals (Hurley et al. Reference Hurley, Briggs, Kippen, Kouveliotou, Meegan, Fishman, Cline and Boer1999, Reference Hurley2013; Sanna et al. Reference Sanna2020). Note that Equation (7) therefore presumes that the only source of timing uncertainty is in the signal cross-correlation, which is a valid approximation in our case as the uncertainty on cross-correlation is of the order
$\Delta \tau_{ij}$
—the measured time difference between the signal arriving at each detector in the network. Classically, this time difference has been computed by binning the light curves observed by each detector with some temporal resolution (which usually depends on the flux of the GRB—brighter bursts can be binned with finer resolution), and then using a cross-correlation algorithm to determine the time offset between the two observed signals (Hurley et al. Reference Hurley, Briggs, Kippen, Kouveliotou, Meegan, Fishman, Cline and Boer1999, Reference Hurley2013; Sanna et al. Reference Sanna2020). Note that Equation (7) therefore presumes that the only source of timing uncertainty is in the signal cross-correlation, which is a valid approximation in our case as the uncertainty on cross-correlation is of the order
![]() ${\sim}$
1 ms (Sanna et al. Reference Sanna2020) whereas the positional uncertainty on the satellite is
${\sim}$
1 ms (Sanna et al. Reference Sanna2020) whereas the positional uncertainty on the satellite is
![]() $<$
30 m (translating to a temporal accuracy of
$<$
30 m (translating to a temporal accuracy of
![]() $<$
20 ns; Fiore et al. Reference Fiore2020) and the detector has an absolute timing accuracy lower than
$<$
20 ns; Fiore et al. Reference Fiore2020) and the detector has an absolute timing accuracy lower than
![]() $0.4\,\mu$
s (Evangelista et al. Reference Evangelista2020).
$0.4\,\mu$
s (Evangelista et al. Reference Evangelista2020).
It has been shown by Burgess et al. (Reference Burgess, Cameron, Svinkin and Greiner2021) that this ‘classical’ triangulation method has limitations, especially for faint bursts when the number of photons per time bin is small. When compared to a full Bayesian treatment of statistical uncertainties, Burgess et al. (Reference Burgess, Cameron, Svinkin and Greiner2021) shows that the classic cross-correlation approach results in an overconfidence of the
![]() $1\sigma$
uncertainty on time delay by a factor of
$1\sigma$
uncertainty on time delay by a factor of
![]() ${\sim}$
${\sim}$
![]() $2-3$
, which translates directly into an overconfidence on the burst localisation. Nevertheless, given this paper is a continuation of the work performed in Sanna et al. (Reference Sanna2020) and given the computational benefits in our Monte Carlo simulation approach, we use the classic cross-correlation approach, and note that our results may contain a systematic uncertainty of 2-3 times our reported statistical localisations for the faintest bursts.
$2-3$
, which translates directly into an overconfidence on the burst localisation. Nevertheless, given this paper is a continuation of the work performed in Sanna et al. (Reference Sanna2020) and given the computational benefits in our Monte Carlo simulation approach, we use the classic cross-correlation approach, and note that our results may contain a systematic uncertainty of 2-3 times our reported statistical localisations for the faintest bursts.
In order to determine the impact that GRB flux has on time delay uncertainty, we adopt the work of Sanna et al. (Reference Sanna2020), where the standard deviation in the cross-correlation uncertainty,
![]() $\sigma_{\text{cc}}$
is reported as a function of average GRB flux for a random sample of 100 long and 100 short GRBs observed by Fermi GBM. Specifically, in this work we use the ‘Flnc_Band_Phtfluxb’ data type from the Fermi GBM catalogue (Gruber et al. Reference Gruber2014; von Kienlin et al. Reference von Kienlin2014, Reference von Kienlin2020; Bhat et al. Reference Bhat2016), which is a quantity related to the burst photon flux between 50 and 300 keV. The results from Sanna et al. (Reference Sanna2020) are reported here in Figure 4 as black data points. In this figure, each data point represents the results from 1 000 Monte-Carlo (MC) simulations which calculated the difference between the true arrival time delay and the value inferred from cross-correlation methods. The resulting distribution of time-offset values is then fit with a Gaussian function with a mean of zero and a standard deviation
$\sigma_{\text{cc}}$
is reported as a function of average GRB flux for a random sample of 100 long and 100 short GRBs observed by Fermi GBM. Specifically, in this work we use the ‘Flnc_Band_Phtfluxb’ data type from the Fermi GBM catalogue (Gruber et al. Reference Gruber2014; von Kienlin et al. Reference von Kienlin2014, Reference von Kienlin2020; Bhat et al. Reference Bhat2016), which is a quantity related to the burst photon flux between 50 and 300 keV. The results from Sanna et al. (Reference Sanna2020) are reported here in Figure 4 as black data points. In this figure, each data point represents the results from 1 000 Monte-Carlo (MC) simulations which calculated the difference between the true arrival time delay and the value inferred from cross-correlation methods. The resulting distribution of time-offset values is then fit with a Gaussian function with a mean of zero and a standard deviation
![]() $\sigma_{cc}$
. To perform 1 000 MC trials for each burst, the GRB light curve observed by Fermi GBM is used as a template from which unique GRB light curves can be generated by both rescaling the detector effective area to match that of the HERMES instrument and applying a Poissonian randomisation of the counts contained in each bin of the template.
$\sigma_{cc}$
. To perform 1 000 MC trials for each burst, the GRB light curve observed by Fermi GBM is used as a template from which unique GRB light curves can be generated by both rescaling the detector effective area to match that of the HERMES instrument and applying a Poissonian randomisation of the counts contained in each bin of the template.

Figure 4. Black points: Standard deviation in the cross-correlation uncertainty (
![]() $\sigma_{\text{cc}}$
) calculated for a sample of 100 long and 100 short GRBs from Sanna et al. (Reference Sanna2020). Red line: Best-fit power-law to the black data points, where the
$\sigma_{\text{cc}}$
) calculated for a sample of 100 long and 100 short GRBs from Sanna et al. (Reference Sanna2020). Red line: Best-fit power-law to the black data points, where the
![]() $1\sigma$
interval is shown in light red.
$1\sigma$
interval is shown in light red.
To generalise the results of Sanna et al. (Reference Sanna2020) we construct a power-law fit to this data (Figure 4, red lines), assuming that the residuals follow a Gaussian distribution. The parameters for our fits are given in Table 1.
We use these relations to compute the uncertainty on signal cross-correlation,
![]() $\sigma_{cc}$
, given the observed flux of a burst, which depends not only on the flux of the GRB as seen from LEO, but also on the incident angle of the burst to the detector (
$\sigma_{cc}$
, given the observed flux of a burst, which depends not only on the flux of the GRB as seen from LEO, but also on the incident angle of the burst to the detector (
![]() $F_{obs} = F_{GRB} \cos \unicode{x03B8}$
).
$F_{obs} = F_{GRB} \cos \unicode{x03B8}$
).
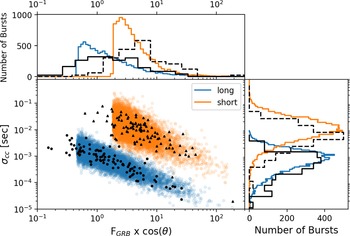
Figure 5 plots the results from
![]() $10^4$
Mote-Carlo trials using this method to calculate the standard deviation on cross-correlation uncertainty. As expected, the satellites in our simulated constellation observe a lower GRB flux on average than those bursts used by Sanna et al. (Reference Sanna2020) (black points/curves), since we take into account the HERMES instruments’ approximate cosine dependence on photon incident angle. Otherwise we find good agreement with the results presented in Sanna et al. (Reference Sanna2020).
$10^4$
Mote-Carlo trials using this method to calculate the standard deviation on cross-correlation uncertainty. As expected, the satellites in our simulated constellation observe a lower GRB flux on average than those bursts used by Sanna et al. (Reference Sanna2020) (black points/curves), since we take into account the HERMES instruments’ approximate cosine dependence on photon incident angle. Otherwise we find good agreement with the results presented in Sanna et al. (Reference Sanna2020).
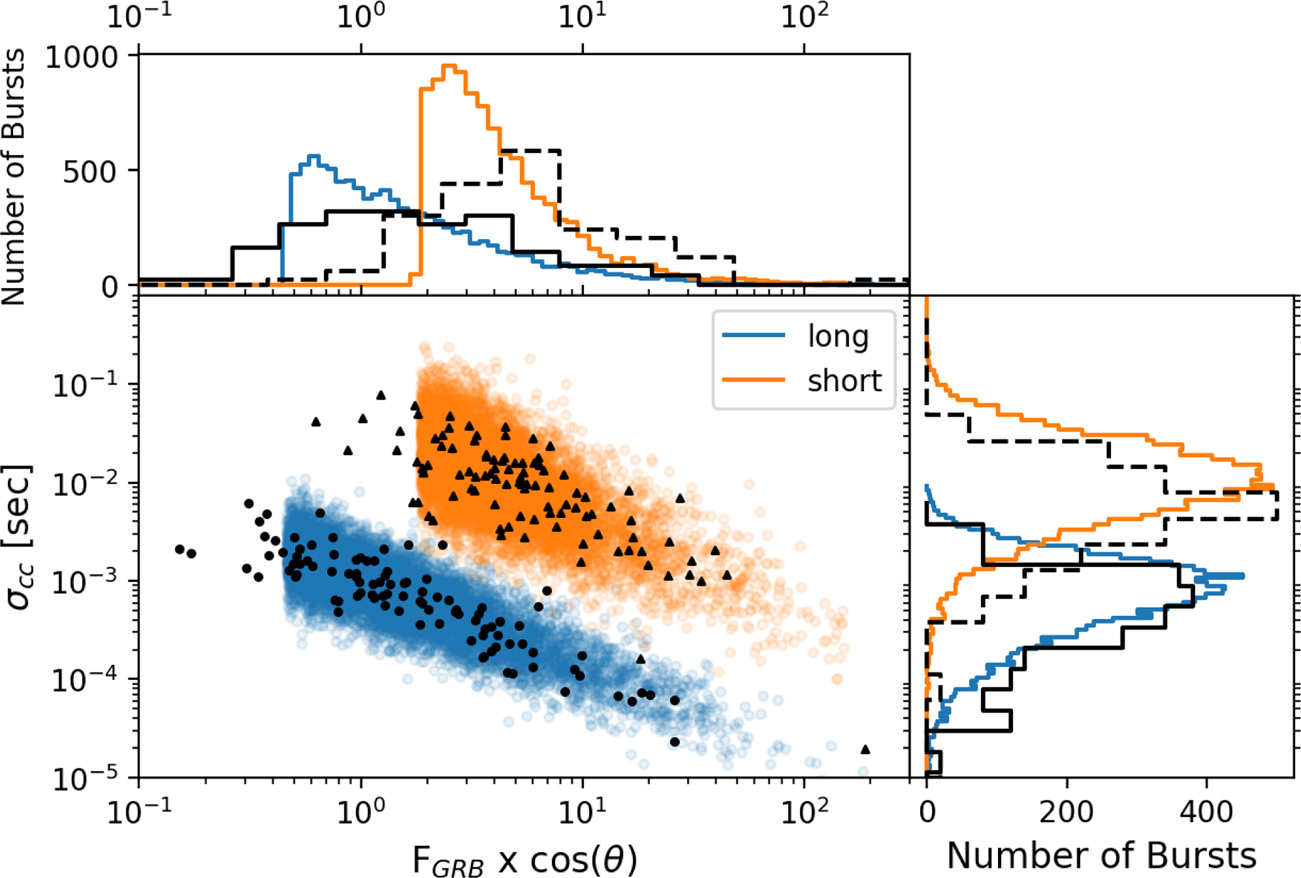
Figure 5. Scatter plot showing the relation between the observed flux of the GRB (
![]() $F_{obs} = F_{GRB}\cos\unicode{x03B8} $
) and the expected standard deviation on timing uncertainty after cross-correlation
$F_{obs} = F_{GRB}\cos\unicode{x03B8} $
) and the expected standard deviation on timing uncertainty after cross-correlation
![]() $\sigma_{cc}$
from
$\sigma_{cc}$
from
![]() $10^4$
MC trials. The top panel plots the distribution of observed average GRB fluxes, and right hand panel show histograms for the resulting distribution of cross-correlation uncertainty as derived from the given flux distributions. For comparison, in black we also plot the 100 long GRBs (circles, solid histograms) and 100 short GRBs (triangles, dashed histograms) from Sanna et al. (Reference Sanna2020) which were used as a basis for our model. We have arbitrarily scaled the histograms of the Sanna et al. (Reference Sanna2020) data by eye so that they match the scale of our simulated data.
$10^4$
MC trials. The top panel plots the distribution of observed average GRB fluxes, and right hand panel show histograms for the resulting distribution of cross-correlation uncertainty as derived from the given flux distributions. For comparison, in black we also plot the 100 long GRBs (circles, solid histograms) and 100 short GRBs (triangles, dashed histograms) from Sanna et al. (Reference Sanna2020) which were used as a basis for our model. We have arbitrarily scaled the histograms of the Sanna et al. (Reference Sanna2020) data by eye so that they match the scale of our simulated data.
Note that this method contains several assumptions, justified by our aim to forecast performance of a future constellation rather than a detailed characterisation of the localisation algorithm applied to actual data. Firstly, we are assuming that average GRB flux is as accurate predictor of cross-correlation uncertainty. For a more realistic simulation, one could follow the same procedure as performed in Sanna et al. (Reference Sanna2020) and perform the cross-correlation of GRB light curves to determine the ‘measured’ arrival time difference.
Secondly, our simulation assumes that the uncertainty on signal cross-correlation between two detectors
![]() $\sigma_{cc,ij}$
is uncorrelated between pairs of detectors. In reality, we would expect this quantity to have some correlation between pairs of satellites, e.g.,
$\sigma_{cc,ij}$
is uncorrelated between pairs of detectors. In reality, we would expect this quantity to have some correlation between pairs of satellites, e.g.,
![]() $\sigma_{cc,ij}$
should have some relation to
$\sigma_{cc,ij}$
should have some relation to
![]() $\sigma_{cc,ik}$
since both involve the signal observed by detector i. However, understanding these correlations is non-trivial, and beyond the scope of this work.
$\sigma_{cc,ik}$
since both involve the signal observed by detector i. However, understanding these correlations is non-trivial, and beyond the scope of this work.
4.5.3. Simulating GRB localisation
For each GRB that meets the conditions defined in Section 4.4 we perform the triangulation procedure described in Section 4.5.1. We start by constructing a set of ‘measured’ time-difference pairs
![]() $\Delta \tau_{ij} = \Delta t_{ij}(\hat d_{GRB}) + \mathcal{N}(0,\sigma_{cc})$
between each satellite which detected the event, where
$\Delta \tau_{ij} = \Delta t_{ij}(\hat d_{GRB}) + \mathcal{N}(0,\sigma_{cc})$
between each satellite which detected the event, where
![]() $\mathcal{N}(0,\sigma_{cc})$
represents a random variable sampled from a Gaussian distribution with a mean of zero and standard deviation
$\mathcal{N}(0,\sigma_{cc})$
represents a random variable sampled from a Gaussian distribution with a mean of zero and standard deviation
![]() $\sigma_{cc}$
, as defined above.
$\sigma_{cc}$
, as defined above.
Using these values we calculate Equation (7) for each point on the sky, where we represent the whole sky using a grid of
![]() $660048$
points uniformly distributed on the celestial sphere (giving each point an area of
$660048$
points uniformly distributed on the celestial sphere (giving each point an area of
![]() ${\sim}$
${\sim}$
![]() $0.0625$
deg
$0.0625$
deg
![]() $^2$
), with positions generated by the Fibonacci lattice method (González Reference González2009). For computational efficiency, in cases where the localisation is not expected to reach
$^2$
), with positions generated by the Fibonacci lattice method (González Reference González2009). For computational efficiency, in cases where the localisation is not expected to reach
![]() $<$
1 deg
$<$
1 deg
![]() $^2$
(e.g., when localising short GRBs, or when testing constellations with fewer satellites in Polar orbit), a grid of 41 253 points (1 deg
$^2$
(e.g., when localising short GRBs, or when testing constellations with fewer satellites in Polar orbit), a grid of 41 253 points (1 deg
![]() $^2$
resolution), or
$^2$
resolution), or
![]() $165012$
points (
$165012$
points (
![]() $0.25$
deg
$0.25$
deg
![]() $^2$
resolution) is used.
$^2$
resolution) is used.
Finally, we determine the 68% or 90% localisation confidence regions using the values defined in Equation (8), excluding those points that are disallowed by LOS arguments as defined in Section 4.5.1.
We note here that when calculating the time-difference pairs
![]() $\Delta \tau_{ij}$
and the timing uncertainty on the signal cross-correlation
$\Delta \tau_{ij}$
and the timing uncertainty on the signal cross-correlation
![]() $\sigma_{cc}$
, we presume that the satellites are stationary for the duration of the burst. In reality, the relative motion of each satellite introduces a small difference in the arrival time of photons at each detector. We estimate that as a worst-case scenario—a satellite in LEO moving at 10 km s
$\sigma_{cc}$
, we presume that the satellites are stationary for the duration of the burst. In reality, the relative motion of each satellite introduces a small difference in the arrival time of photons at each detector. We estimate that as a worst-case scenario—a satellite in LEO moving at 10 km s
![]() $^{-1}$
in the direction of the burst—would detect the final photon from a typical long GRB (approximately
$^{-1}$
in the direction of the burst—would detect the final photon from a typical long GRB (approximately
![]() ${\sim}$
10 s)
${\sim}$
10 s)
![]() $0.3$
ms before a stationary satellite, meaning that the moving satellite would effectively observe the signal of the GRB ‘compressed’ in time by
$0.3$
ms before a stationary satellite, meaning that the moving satellite would effectively observe the signal of the GRB ‘compressed’ in time by
![]() $0.3$
ms, which is comparable to the cross-correlation accuracy achieved for the brightest
$0.3$
ms, which is comparable to the cross-correlation accuracy achieved for the brightest
![]() ${\sim}$
20% of long GRBs. However, given the position and velocity of each satellite in the SpIRIT + HERMES constellation are known to a high accuracy, in principle this effect is entirely deterministic and can be accounted for in a sufficiently sophisticated cross-correlation algorithm. For this reason, we choose to neglect the relative motion of each satellite in this work, leaving its inclusion to a future simulation of the HERMES constellation’s localisation capabilities, and note that this assumption may introduce some systematic uncertainty into our results for the best localised long GRBs.
${\sim}$
20% of long GRBs. However, given the position and velocity of each satellite in the SpIRIT + HERMES constellation are known to a high accuracy, in principle this effect is entirely deterministic and can be accounted for in a sufficiently sophisticated cross-correlation algorithm. For this reason, we choose to neglect the relative motion of each satellite in this work, leaving its inclusion to a future simulation of the HERMES constellation’s localisation capabilities, and note that this assumption may introduce some systematic uncertainty into our results for the best localised long GRBs.
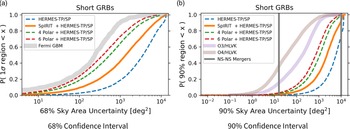
5. Results and discussion
Following the method outlined in Section 4.4, we simulate the localisation capabilities of HERMES-TP/SP, as well as SpIRIT + HERMES-TP/SP and constellations featuring additional SpIRIT-like satellites in Polar orbit. The following sections present the localisation results for a sample of
![]() $10^4$
long and
$10^4$
long and
![]() $10^4$
short GRBs.
$10^4$
short GRBs.
5.1. Constellation sky coverage
Figure 3 demonstrates that the combined SpIRIT + HERMES-TP/SP constellation is only able to detect a maximum of 60% of long GRBs and
![]() ${\sim}$
50% of short GRBs, which is to be expected since the FWHM of the HERMES instrument is
${\sim}$
50% of short GRBs, which is to be expected since the FWHM of the HERMES instrument is
![]() $60^{\circ}$
meaning that each FOV covers
$60^{\circ}$
meaning that each FOV covers
![]() ${\sim}$
25% of the sky at FWHM, and the constellation is divided into two co-pointing groups. We note that the constellation is able to detect a higher fraction of long GRBs than short GRBs because of the different limits we have placed on the average flux sensitivity for the two types of burst (see Section 4.4).
${\sim}$
25% of the sky at FWHM, and the constellation is divided into two co-pointing groups. We note that the constellation is able to detect a higher fraction of long GRBs than short GRBs because of the different limits we have placed on the average flux sensitivity for the two types of burst (see Section 4.4).
We find that for a constellation with a single satellite in polar orbit, approximately
![]() ${\sim}$
10% of bursts can be detected by four orbital elements simultaneously (SpIRIT + all three satellites in one of the HERMES triplets). This low fraction is both due to the transit of each orbital element through high particle flux regions (e.g., SpIRIT over the poles and through the SAA; HERMES through the edge of the SAA), as well as in part of each satellite’s FOV being obstructed by the Earth at the point in its orbit when Earth is perpendicular to its LOS.
${\sim}$
10% of bursts can be detected by four orbital elements simultaneously (SpIRIT + all three satellites in one of the HERMES triplets). This low fraction is both due to the transit of each orbital element through high particle flux regions (e.g., SpIRIT over the poles and through the SAA; HERMES through the edge of the SAA), as well as in part of each satellite’s FOV being obstructed by the Earth at the point in its orbit when Earth is perpendicular to its LOS.
For a constellation of 4 Polar satellites + HERMES-TP/SP we find similarly that only
![]() ${\sim}$
10% of GRBs can be detected by the all 5 of the co-pointing satellites (2 Polar satellites + 3 HERMES-TP/SP satellites), while
${\sim}$
10% of GRBs can be detected by the all 5 of the co-pointing satellites (2 Polar satellites + 3 HERMES-TP/SP satellites), while
![]() ${\sim}$
25% of bursts are detected by four satellites (1 Polar satellite + 3 HERMES-TP/SP, or two Polar satellites + 2 HERMES-TP/SP), with one satellite missing the observation due to crossing a high particle flux region or LOS obstruction. The case is similar for six Polar satellites, where
${\sim}$
25% of bursts are detected by four satellites (1 Polar satellite + 3 HERMES-TP/SP, or two Polar satellites + 2 HERMES-TP/SP), with one satellite missing the observation due to crossing a high particle flux region or LOS obstruction. The case is similar for six Polar satellites, where
![]() $\lesssim$
10% of bursts are detected by all of the co-pointing satellites due to the intermittent passage of each orbital element through a region of high particle flux.
$\lesssim$
10% of bursts are detected by all of the co-pointing satellites due to the intermittent passage of each orbital element through a region of high particle flux.
In the case of launching additional Polar satellites, the benefit comes from the fact that each burst is detected by a larger number of satellites on average. For example, in the case of a single Polar satellite, only 10% of bursts are detected by four satellites, while with six Polar satellites
![]() ${\sim}$
40% of GRBs are detected by four or more satellites, enabling more accurate burst localisations on average despite the fact that not all Polar satellites are observing the event.
${\sim}$
40% of GRBs are detected by four or more satellites, enabling more accurate burst localisations on average despite the fact that not all Polar satellites are observing the event.
5.2. SpIRIT + HERMES-TP/SP localisation
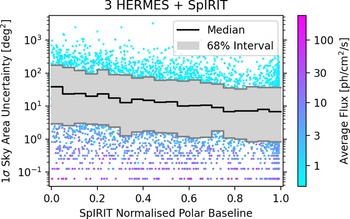
The primary advantage of augmenting the HERMES-TP/SP constellation with the SpIRIT satellite is that the additional detector in Polar orbit greatly reduces the localisation degeneracy in declination when SpIRIT is located at high latitudes.
Because each satellite in the HERMES-TP/SP constellation orbits in the equatorial plane and align their LOS in the same direction, there is limited accuracy and intrinsic degeneracy in the declination coordinate of the burst—for example, it is equally possible that a burst came from declination
![]() $\delta = 30^{\circ}$
or
$\delta = 30^{\circ}$
or
![]() $\delta = -30^{\circ}$
. However, SpIRIT’s Polar orbit gives a large average baseline perpendicular to the orbital plane of the HERMES-TP/SP, which allows for the degeneracy in declination to be broken if SpIRIT is able to detect the event. Indeed, even if SpIRIT doesn’t directly detect the event while co-pointing with the other observing satellites, a non-detection would still provide useful information to rule out uncertainty regions enclosed in SpIRIT’s FoV. An example uncertainty region for HERMES-TP/SP and SpIRIT + HERMES-TP/SP is given in Figure 6, which demonstrates the increased localisation accuracy in the declination coordinate when including SpIRIT.
$\delta = -30^{\circ}$
. However, SpIRIT’s Polar orbit gives a large average baseline perpendicular to the orbital plane of the HERMES-TP/SP, which allows for the degeneracy in declination to be broken if SpIRIT is able to detect the event. Indeed, even if SpIRIT doesn’t directly detect the event while co-pointing with the other observing satellites, a non-detection would still provide useful information to rule out uncertainty regions enclosed in SpIRIT’s FoV. An example uncertainty region for HERMES-TP/SP and SpIRIT + HERMES-TP/SP is given in Figure 6, which demonstrates the increased localisation accuracy in the declination coordinate when including SpIRIT.

Figure 6. Comparison of the 68% (yellow) and 90% (teal) confidence regions for the location of a long GRB as measured by the HERMES-TP/SP and by the SpIRIT + HERMES-TP/SP constellations for one realisation in our Monte Carlo simulation. The red cross denotes the location of the GRB on the sky. The grey lines represent the
![]() $1\sigma$
error annuli between each pair of satellites in the HERMES constellation. The gold lines represent the error annuli for the three additional satellite pairs that can be made when SpIRIT is included in the HERMES-TP/SP.
$1\sigma$
error annuli between each pair of satellites in the HERMES constellation. The gold lines represent the error annuli for the three additional satellite pairs that can be made when SpIRIT is included in the HERMES-TP/SP.
It should be noted that another way to resolve this degeneracy is by adjusting the pointing direction of each satellite so that they do not co-point at the same field. Doing so could allow the constellation to exploit the HERMES instruments’ cosine dependence on photon incident angle to localise bursts by taking into account the ratio of GRB fluence at each detector. However, this would lead to a trade-off between GRB localisation accuracy and number of GRBs localised, since a smaller fraction of the sky would be observed by all three satellites. This trade-off is something that will be explored in future work.
Figure 7 plots the area of the
![]() $1\sigma$
localisation region for long GRBs detected by SpIRIT + 3 HERMES-TP/SP satellites against SpIRIT’s distance from the equatorial plane, where we have colour-coded each data point by the average flux of the GRB. While the localisation accuracy depends strongly on the flux of the GRB, we find that SpIRIT’s Polar orbit is able to dramatically improve burst localisations, such that the constellation’s capabilities improve by a factor of
$1\sigma$
localisation region for long GRBs detected by SpIRIT + 3 HERMES-TP/SP satellites against SpIRIT’s distance from the equatorial plane, where we have colour-coded each data point by the average flux of the GRB. While the localisation accuracy depends strongly on the flux of the GRB, we find that SpIRIT’s Polar orbit is able to dramatically improve burst localisations, such that the constellation’s capabilities improve by a factor of
![]() ${\sim}$
5 when SpIRIT is over the poles compared to when it is at the equator. When SpIRIT is close to its maximum distance from the equatorial plane, we expect to achieve statistical burst localisations within
${\sim}$
5 when SpIRIT is over the poles compared to when it is at the equator. When SpIRIT is close to its maximum distance from the equatorial plane, we expect to achieve statistical burst localisations within
![]() ${\sim}$
10 deg
${\sim}$
10 deg
![]() $^2$
for 50% of long GRBs, and localisations within a few square degrees for bursts with an observed time-averaged flux higher than
$^2$
for 50% of long GRBs, and localisations within a few square degrees for bursts with an observed time-averaged flux higher than
![]() ${\sim}$
5ph cm
${\sim}$
5ph cm
![]() $^{-2}$
s
$^{-2}$
s
![]() $^{-1}$
(
$^{-1}$
(
![]() ${\sim}$
15% of long GRBs).
${\sim}$
15% of long GRBs).
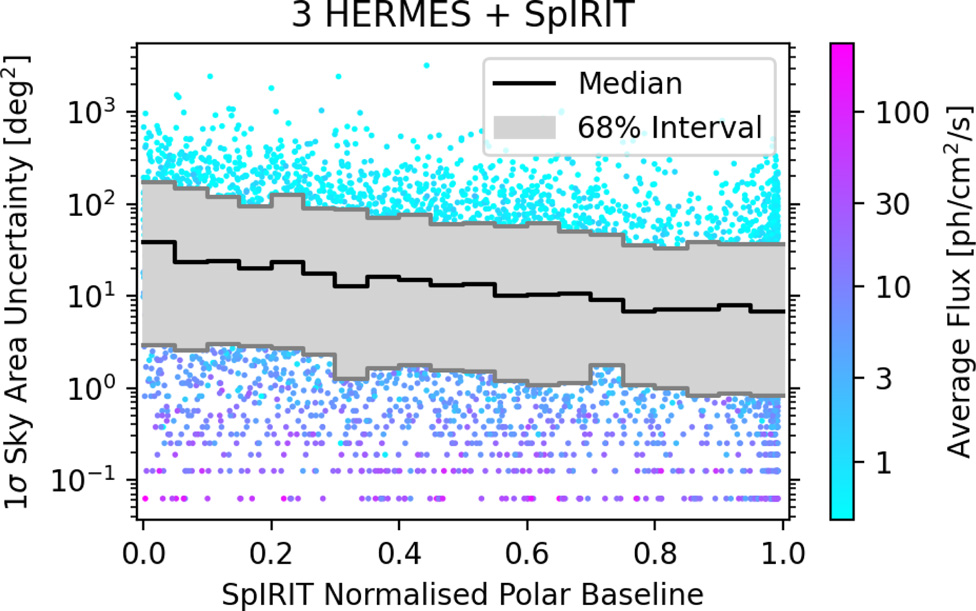
Figure 7. Plot of the
![]() $1\sigma$
localisation region for
$1\sigma$
localisation region for
![]() ${\sim}$
${\sim}$
![]() $10^4$
simulated long GRB events observed by the SpIRIT + HERMES-TP/SP constellation. The x-axis shows SpIRIT’s baseline perpendicular to the equatorial plane for each burst normalised by its maximum baseline (maximum baseline = Earth radius + 550 km orbital altitude). Note here that ‘baseline’ refers to SpIRIT’s distance perpendicular to the equatorial plane. The black line shows the median of the data points within the bin (binned into intervals of 0.05 on normalised Polar baseline), and the grey region contains the central 68% of data in each bin. Individual data points are shown for outliers, with the colour denoting the average flux of the GRB.
$10^4$
simulated long GRB events observed by the SpIRIT + HERMES-TP/SP constellation. The x-axis shows SpIRIT’s baseline perpendicular to the equatorial plane for each burst normalised by its maximum baseline (maximum baseline = Earth radius + 550 km orbital altitude). Note here that ‘baseline’ refers to SpIRIT’s distance perpendicular to the equatorial plane. The black line shows the median of the data points within the bin (binned into intervals of 0.05 on normalised Polar baseline), and the grey region contains the central 68% of data in each bin. Individual data points are shown for outliers, with the colour denoting the average flux of the GRB.
Note that while in the context of our simulation the constellation achieves localisations
![]() $<$
1 deg
$<$
1 deg
![]() $^2$
for very bright bursts when SpIRIT is near the poles, quantifying with precision such cases goes beyond the simplifying assumptions upon which our framework is based.
$^2$
for very bright bursts when SpIRIT is near the poles, quantifying with precision such cases goes beyond the simplifying assumptions upon which our framework is based.
In the following analysis we divide our results into long and short GRBs.
5.2.1. Long GRBs
Figure 8 compares the cumulative distributions of the
![]() $1\sigma$
localisation region for
$1\sigma$
localisation region for
![]() $10^4$
long GRBs localised by HERMES-TP/SP and SpIRIT + HERMES-TP/SP. For comparison we also plot the 68% statistical sky area uncertainties reported in the fourth Fermi/GBM catalogue (von Kienlin et al. Reference von Kienlin2020). Note here that we are comparing the statistical GRB localisation capabilities only—while both instruments also have an associated systematic uncertainty, we cannot estimate these for the nano-satellite constellation since to do so would require in-flight data, which is impossible since the constellation has not been launched yet. For reference, the systematic uncertainty for Fermi GBM is approximately
$10^4$
long GRBs localised by HERMES-TP/SP and SpIRIT + HERMES-TP/SP. For comparison we also plot the 68% statistical sky area uncertainties reported in the fourth Fermi/GBM catalogue (von Kienlin et al. Reference von Kienlin2020). Note here that we are comparing the statistical GRB localisation capabilities only—while both instruments also have an associated systematic uncertainty, we cannot estimate these for the nano-satellite constellation since to do so would require in-flight data, which is impossible since the constellation has not been launched yet. For reference, the systematic uncertainty for Fermi GBM is approximately
![]() ${\sim}$
${\sim}$
![]() $2-4^{\circ}$
(Goldstein et al. Reference Goldstein2020), and it will likely be comparable to this for the nano-satellite constellation.
$2-4^{\circ}$
(Goldstein et al. Reference Goldstein2020), and it will likely be comparable to this for the nano-satellite constellation.

Figure 8. Cumulative probability of localising a long GRB within a given
![]() $1\sigma$
region on the sky for n SpIRIT-like satellites in Polar orbit + HERMES-TP/SP. The
$1\sigma$
region on the sky for n SpIRIT-like satellites in Polar orbit + HERMES-TP/SP. The
![]() $n_{\text{polar}} = 0$
constellation (blue line) represents the HERMES-TP/SP constellation operating alone.
$n_{\text{polar}} = 0$
constellation (blue line) represents the HERMES-TP/SP constellation operating alone.

Figure 9. Cumulative probability of localising a short GRB within a given area on the sky for n SpIRIT-like satellites in Polar orbit + HERMES-TP/SP. The
![]() $n_{\text{polar}} = 0$
constellation (blue line) represents the HERMES-TP/SP constellation operating alone. Left: 68% confidence intervals. Right: 90% confidence intervals. The dashed lines represent the highest expected localisation capabilities of the advanced LIGO Hanford and Livingstone, advanced VIRGO and KAGRA GW detectors to localise BNS coalescences in O3 and O4, respectively (note that for O3, detector sensitivities were taken to be representative of the first 3 months of observations for aLIGO Hanford and Livingston, and AdV, and the highest expected O3 sensitivity for KAGRA). See Abbott et al. (Reference Abbott2020) Figure 6 for details). The two vertical grey lines represent the prompt reported 90% confidence regions for the two binary neutron star coalescences observed to date; GW170817, and GW190425.
$n_{\text{polar}} = 0$
constellation (blue line) represents the HERMES-TP/SP constellation operating alone. Left: 68% confidence intervals. Right: 90% confidence intervals. The dashed lines represent the highest expected localisation capabilities of the advanced LIGO Hanford and Livingstone, advanced VIRGO and KAGRA GW detectors to localise BNS coalescences in O3 and O4, respectively (note that for O3, detector sensitivities were taken to be representative of the first 3 months of observations for aLIGO Hanford and Livingston, and AdV, and the highest expected O3 sensitivity for KAGRA). See Abbott et al. (Reference Abbott2020) Figure 6 for details). The two vertical grey lines represent the prompt reported 90% confidence regions for the two binary neutron star coalescences observed to date; GW170817, and GW190425.

Figure 10. Localisation histograms for the sample of
![]() $10^4$
GRBs detected by the SpIRIT + HERMES-TP/SP Constellation. The blue curve represents the full sample of simulated GRBs, while the orange and green curves compare the localisation capabilities of the constellation when SpIRIT either detects or does not detect the burst. Left: Long GRB sample. Right: Short GRB sample.
$10^4$
GRBs detected by the SpIRIT + HERMES-TP/SP Constellation. The blue curve represents the full sample of simulated GRBs, while the orange and green curves compare the localisation capabilities of the constellation when SpIRIT either detects or does not detect the burst. Left: Long GRB sample. Right: Short GRB sample.
The inclusion of SpIRIT greatly enhances the accuracy of GRB localisations compared to the HERMES-TP/SP alone. SpIRIT + HERMES-TP/SP is able to localise 60% of long GRBs within
![]() ${\sim}$
28 deg
${\sim}$
28 deg
![]() $^2$
, which corresponds to an uncertainty radius on the sky of
$^2$
, which corresponds to an uncertainty radius on the sky of
![]() ${\sim}$
${\sim}$
![]() $3^{\circ}$
(presuming the uncertainty region is circular), and 90% of long GRBs within 150 deg
$3^{\circ}$
(presuming the uncertainty region is circular), and 90% of long GRBs within 150 deg
![]() $^2$
(
$^2$
(
![]() ${\sim}$
${\sim}$
![]() $7^{\circ}$
radius). In reality the uncertainty regions are irregular in shape, but a circle is a good approximation when the burst is relatively well localised. This represents an improvement by a factor of
$7^{\circ}$
radius). In reality the uncertainty regions are irregular in shape, but a circle is a good approximation when the burst is relatively well localised. This represents an improvement by a factor of
![]() ${\sim}$
5 over the HERMES-TP/SP alone, which is only able to localise
${\sim}$
5 over the HERMES-TP/SP alone, which is only able to localise
![]() ${\sim}$
50% of GRBs to within 100 deg
${\sim}$
50% of GRBs to within 100 deg
![]() $^2$
on the sky.
$^2$
on the sky.
Figure 8 shows that the combined SpIRIT + HERMES-TP/SP constellation will have statistical GRB localisation capabilities comparable to those reported by Fermi GBM. This result demonstrates the potential cost-effectiveness of using modular nano-satellite astronomy to achieve specific science goals, as a constellation of several relatively inexpensive nano-satellites is expected to achieve a localisation accuracy similar to the substantially more complex and expensive Fermi GBM. In fact, estimating an approximate cost of US $150M for the Fermi GBM instrument (
![]() ${\sim}$
25% of the total cost of the mission (Fermi Gamma-ray Space Telescope Q&A on the GLAST MissionFootnote f)) and of US $2.5M for each element of the nano-satellite constellation, there is a possible factor 10x in savings using a distributed-aperture solution for localising long GRB afterglows. We note however that the disadvantage to using a HERMES-like distributed-aperture solution with the current design is sky coverage: the Fermi GBM can observe over half the sky at any time (i.e., the whole sky not obstructed by the Earth Meegan et al. Reference Meegan2009), whereas the FoV of a single HERMES instrument only achieves
${\sim}$
25% of the total cost of the mission (Fermi Gamma-ray Space Telescope Q&A on the GLAST MissionFootnote f)) and of US $2.5M for each element of the nano-satellite constellation, there is a possible factor 10x in savings using a distributed-aperture solution for localising long GRB afterglows. We note however that the disadvantage to using a HERMES-like distributed-aperture solution with the current design is sky coverage: the Fermi GBM can observe over half the sky at any time (i.e., the whole sky not obstructed by the Earth Meegan et al. Reference Meegan2009), whereas the FoV of a single HERMES instrument only achieves
![]() ${\sim}$
25% sky coverage at FWHM, meaning that achieving all-sky coverage with a nano-satellite constellation with overlapped FoV’s would partially offset the cost savings (although there would be further gains from mass production of the constellation elements). Furthermore, it is non-trivial to achieve maximal overlap of the FOV of each nano-satellite element, as it requires continual optimisation of the pointing directions of each satellite to account for orbital drift and different orbital configurations (Colagrossi et al. Reference Colagrossi, Prinetto, Silvestrini and Lavagna2020).
${\sim}$
25% sky coverage at FWHM, meaning that achieving all-sky coverage with a nano-satellite constellation with overlapped FoV’s would partially offset the cost savings (although there would be further gains from mass production of the constellation elements). Furthermore, it is non-trivial to achieve maximal overlap of the FOV of each nano-satellite element, as it requires continual optimisation of the pointing directions of each satellite to account for orbital drift and different orbital configurations (Colagrossi et al. Reference Colagrossi, Prinetto, Silvestrini and Lavagna2020).
5.2.2. Short GRBs
Figure 9 compares the localisation capabilities of the HERMES-TP/SP and combined SpIRIT + HERMES-TP/SP constellations to both the Fermi GBM (where we have plot the Fermi localisation uncertainty using same method as discussed in Section 5.2.1) and to the theoretical current and future localisation capabilities of the Advanced LIGO Hanford and Livingston, Advanced VIRGO and KAGRA gravitational wave detectors (Abbott et al. Reference Abbott2020; 90% confidence regions, Figure 9b). Note that this reflects the predicted performance of the four gravitational wave detectors operating concurrently during O3 and O4—in reality KAGRA did not participate in O3, but is planned for joint operation in O4. We have also included the reported prompt localisations for both of the BNS coalescences observed by GW detectors; GW170817 (Abbott et al. Reference Abbott2020) and GW190425 (Abbott et al. Reference Abbott2021). While the error box for GW190425 was later refined, here we compare the prompt localisation capability to ensure a fair comparison to a nano-satellite constellation. Note that the HERMES-TP/SP constellation is less effective at localising short GRBs compared to long GRBs due to the increased difficulty in precise signal cross-correlation for short GRBs, although a future instrument redesign with increased collecting area would mitigate this current limitation (Sanna et al. Reference Sanna2020).
The addition of SpIRIT to HERMES-TP/SP is able to substantially improve the localisation of short GRBs. HERMES-TP/SP alone has a 90%
![]() $1\sigma$
localisation range of
$1\sigma$
localisation range of
![]() ${\sim}$
215–13000 deg
${\sim}$
215–13000 deg
![]() $^2$
, while the SpIRIT + HERMES-TP/SP constellation’s 90%
$^2$
, while the SpIRIT + HERMES-TP/SP constellation’s 90%
![]() $1\sigma$
range is
$1\sigma$
range is
![]() ${\sim}$
50–8450 deg
${\sim}$
50–8450 deg
![]() $^2$
, where we have defined the 90%
$^2$
, where we have defined the 90%
![]() $1\sigma$
localisation interval as the range of
$1\sigma$
localisation interval as the range of
![]() $1\sigma$
confidence regions spanning 5–95% of the cumulative distribution.
$1\sigma$
confidence regions spanning 5–95% of the cumulative distribution.
Despite this improvement in the constellation’s ability to localise short GRBs, in terms of multi-messenger observations of short GRBs/BNS coalescences the combined SpIRIT + HERMES-TP/SP constellation is not expected to dramatically improve upon existing capabilities to localise these sources. Not only is the Fermi GBM more effective by a factor of
![]() ${\sim} 5-10\times$
at the EM localisation of short GRBs, but current-generation GW instruments are theoretically capable of localising
${\sim} 5-10\times$
at the EM localisation of short GRBs, but current-generation GW instruments are theoretically capable of localising
![]() $>$
50% of short GRBs within
$>$
50% of short GRBs within
![]() ${\sim}$
200 deg
${\sim}$
200 deg
![]() $^2$
(and within
$^2$
(and within
![]() ${\sim}$
40 deg
${\sim}$
40 deg
![]() $^2$
in the future O4 observing runs) from the GW signal alone (Abbott et al. Reference Abbott2020), which exceeds the localisation capabilities of the nano-satellite constellation. Therefore, in the domain of multi-messenger astronomy the utility of the SpIRIT + HERMES-TP/SP constellation will be in the constellation’s sky coverage (
$^2$
in the future O4 observing runs) from the GW signal alone (Abbott et al. Reference Abbott2020), which exceeds the localisation capabilities of the nano-satellite constellation. Therefore, in the domain of multi-messenger astronomy the utility of the SpIRIT + HERMES-TP/SP constellation will be in the constellation’s sky coverage (
![]() ${\sim}$
50%) and flux sensitivity, which gives it a high probability of detecting the electromagnetic counterpart to a compact binary event observed by GW detectors. Such dual detections are critically needed to improve our understanding of these compact binary mergers, as currently only one simultaneous detection of the GW signal from a BNS merger (GW170817) and a short GRB (GRB170817A) has been recorded to date (Abbott et al. Reference Abbott2017a).
${\sim}$
50%) and flux sensitivity, which gives it a high probability of detecting the electromagnetic counterpart to a compact binary event observed by GW detectors. Such dual detections are critically needed to improve our understanding of these compact binary mergers, as currently only one simultaneous detection of the GW signal from a BNS merger (GW170817) and a short GRB (GRB170817A) has been recorded to date (Abbott et al. Reference Abbott2017a).
5.2.3. Utilising SpIRIT non-detections
The inclusion of SpIRIT into the HERMES-TP/SP enables improvements to the GRB localisation capabilities of the HERMES-TP/SP both when SpIRIT directly detects the burst, but also when SpIRIT does not directly detect the burst. The improvement in the latter case is a product of SpIRIT’s high inclination orbit, since when SpIRIT is over the poles then a considerable section of the HERMES triplet’s FOV is obstructed by the Earth from SpIRIT’s perspective. This means that a SpIRIT non-detection can impose relatively strong constraints on possible source location under these conditions, assuming that SpIRIT is co-pointing at the same field as the HERMES triplet that detects the burst, and that the noise level is low enough for SpIRIT that we would expect to detect the GRB signal.
Figure 10 compares the size of the
![]() $1\sigma$
confidence region for long and short GRBs, where the results have been divided depending on whether SpIRIT detects the GRB or not. Note that in all cases, SpIRIT is co-pointing with the HERMES triplet that detects the GRB. In both cases, we find that SpIRIT makes a direct detection of the GRB for
$1\sigma$
confidence region for long and short GRBs, where the results have been divided depending on whether SpIRIT detects the GRB or not. Note that in all cases, SpIRIT is co-pointing with the HERMES triplet that detects the GRB. In both cases, we find that SpIRIT makes a direct detection of the GRB for
![]() ${\sim}$
85% of bursts in our ‘observable’ sample, which represents the average fraction of the HERMES triplet’s FOV that is simultaneously observed by SpIRIT.
${\sim}$
85% of bursts in our ‘observable’ sample, which represents the average fraction of the HERMES triplet’s FOV that is simultaneously observed by SpIRIT.
In the case of long GRBs we find that the size of the
![]() $1\sigma$
localisation region is always smaller when SpIRIT directly detects the burst compared to when SpIRIT does not detect the GRB. This is to be expected, since for HERMES-TP/SP the typical size of the long GRB localisation region is much lower than the sky coverage of the triplet, meaning that a SpIRIT non-detection will only improve the source localisation in the unlikely case that the burst occurs at coordinates close to the edge of Earth as seen from SpIRIT’s perspective.
$1\sigma$
localisation region is always smaller when SpIRIT directly detects the burst compared to when SpIRIT does not detect the GRB. This is to be expected, since for HERMES-TP/SP the typical size of the long GRB localisation region is much lower than the sky coverage of the triplet, meaning that a SpIRIT non-detection will only improve the source localisation in the unlikely case that the burst occurs at coordinates close to the edge of Earth as seen from SpIRIT’s perspective.
Conversely, in the case of short GRBs we find that in some cases it is possible to achieve more accurate GRB localisations when SpIRIT does not detect the burst. These cases arise for faint short GRBs where the typical uncertainty on signal cross-correlation is large, meaning that the typical
![]() $1\sigma$
localisation region is comparable to the sky coverage of the constellation (
$1\sigma$
localisation region is comparable to the sky coverage of the constellation (
![]() ${\geq}$
${\geq}$
![]() $10^4$
deg
$10^4$
deg
![]() $^2$
). In such cases, SpIRIT non-detections enable more accurate GRB localisations as they restrict the possible location of the GRB to those regions of sky that are obstructed by the Earth at the time of the burst, which is why there are practically no bursts with
$^2$
). In such cases, SpIRIT non-detections enable more accurate GRB localisations as they restrict the possible location of the GRB to those regions of sky that are obstructed by the Earth at the time of the burst, which is why there are practically no bursts with
![]() $1\sigma$
localisation regions larger than
$1\sigma$
localisation regions larger than
![]() ${\sim}$
${\sim}$
![]() $5\times10^3$
deg
$5\times10^3$
deg
![]() $^2$
in the green curve in Figure 10 (right panel).
$^2$
in the green curve in Figure 10 (right panel).
5.3. Additional Polar satellites
After demonstrating the benefits of adding one Polar satellite to the HERMES-TP/SP constellation, it is natural to investigate the localisation potential of launching additional satellites into Polar orbit.
Specifically, we compare constellations featuring 2, 4, and 6 SpIRIT-like satellites in Polar orbit (plus HERMES-TP/SP), since these constellations ensure that either one, two or three Polar satellites are observing each of the co-pointing directions of the HERMES-TP/SP. For example, the localisation capabilities that we present for the
![]() $n_{\text{polar}} = 4$
constellation are a product of observation from 3 equatorial HERMES-TP/SP satellites plus 2 Polar SpIRIT-like satellites (see Figure 3).
$n_{\text{polar}} = 4$
constellation are a product of observation from 3 equatorial HERMES-TP/SP satellites plus 2 Polar SpIRIT-like satellites (see Figure 3).
5.3.1. Long GRBs
Figure 8 demonstrates that a constellation of four Polar satellites plus HERMES-TP/SP would improve the localisation capabilities of the constellation by a factor of
![]() ${\sim}$
2 over the case of a constellation with only one Polar satellite and would be capable of localising 60% of long GRBs to within
${\sim}$
2 over the case of a constellation with only one Polar satellite and would be capable of localising 60% of long GRBs to within
![]() ${\sim}$
10 deg
${\sim}$
10 deg
![]() $^2$
of random uncertainty on the sky (
$^2$
of random uncertainty on the sky (
![]() ${\sim}$
${\sim}$
![]() $2^{\circ}$
radius). A constellation of six Polar satellites would reflect a further improvement by an additional factor of
$2^{\circ}$
radius). A constellation of six Polar satellites would reflect a further improvement by an additional factor of
![]() ${\sim}$
${\sim}$
![]() $1.5$
(or equivalently a
$1.5$
(or equivalently a
![]() $4\times$
improvement over the case of a single Polar satellite) and could enable the localisation of
$4\times$
improvement over the case of a single Polar satellite) and could enable the localisation of
![]() ${\sim}$
50% of long GRBs to within a radius of
${\sim}$
50% of long GRBs to within a radius of
![]() $1^{\circ}$
on the sky.
$1^{\circ}$
on the sky.
Despite the substantial improvement over the case of a single Polar-orbiting satellite, GRB localisations with an error radius of
![]() ${\sim}$
${\sim}$
![]() $1^{\circ}$
are not accurate enough to enable reliable afterglow follow-up observations from existing ground or space-based observatories, most of which have a FoV of the order
$1^{\circ}$
are not accurate enough to enable reliable afterglow follow-up observations from existing ground or space-based observatories, most of which have a FoV of the order
![]() $10 \times 10$
arcmin
$10 \times 10$
arcmin
![]() $^2$
, e.g., GROND:
$^2$
, e.g., GROND:
![]() $10' \times 10'$
(Greiner et al. Reference Greiner2008), Swift UVOT:
$10' \times 10'$
(Greiner et al. Reference Greiner2008), Swift UVOT:
![]() $17' \times 17'$
(Troja Reference Troja2020), Gemini Multi-Object Spectrograph (GMOS):
$17' \times 17'$
(Troja Reference Troja2020), Gemini Multi-Object Spectrograph (GMOS):
![]() $5'.5 \times 5'.5$
(Hook et al. Reference Hook, Jørgensen, Allington-Smith, Davies, Metcalfe, Murowinski and Crampton2004). Taking effective advantage of these GRB detections at high energy for infrared follow-up may, however, be possible in the future with
$5'.5 \times 5'.5$
(Hook et al. Reference Hook, Jørgensen, Allington-Smith, Davies, Metcalfe, Murowinski and Crampton2004). Taking effective advantage of these GRB detections at high energy for infrared follow-up may, however, be possible in the future with
![]() $\gtrsim$
1 deg
$\gtrsim$
1 deg
![]() $^2$
FoV space-based telescopes with rapid repointing capabilities, such as the SkyHopper nano-satellite concept (Thomas et al. Reference Thomas2022).
$^2$
FoV space-based telescopes with rapid repointing capabilities, such as the SkyHopper nano-satellite concept (Thomas et al. Reference Thomas2022).
5.3.2. Short GRBs
As Figure 9 demonstrates, launching a constellation of 4 or 6 Polar orbiting satellites into Polar orbit can improve short GRB localisations by a factor of
![]() ${\sim}$
2–4 over a constellation with a single Polar satellite, achieving a 90%
${\sim}$
2–4 over a constellation with a single Polar satellite, achieving a 90%
![]() $1\sigma$
short GRB localisation range between
$1\sigma$
short GRB localisation range between
![]() ${\sim}$
20 and 4100 deg
${\sim}$
20 and 4100 deg
![]() $^2$
(4 Polar) and 12–2850 deg
$^2$
(4 Polar) and 12–2850 deg
![]() $^2$
(6 Polar), respectively. These improvements enable the statistical localisation of short GRBs with an accuracy close to that reported by Fermi GBM for a small fraction of the best-localised bursts, meaning that such an expanded nano-satellite constellation could be valuable in the near real-time localisation of EM counterparts to BNS coalescences, especially in cases where a short GRB is observed by both Fermi GBM and the nano-satellite constellation (which is likely, given Fermi GBM observes such a large fraction of the sky).
$^2$
(6 Polar), respectively. These improvements enable the statistical localisation of short GRBs with an accuracy close to that reported by Fermi GBM for a small fraction of the best-localised bursts, meaning that such an expanded nano-satellite constellation could be valuable in the near real-time localisation of EM counterparts to BNS coalescences, especially in cases where a short GRB is observed by both Fermi GBM and the nano-satellite constellation (which is likely, given Fermi GBM observes such a large fraction of the sky).
At the time of writing, real time triggers and
![]() $1\sigma$
localisations for short GRBs can be obtained with accuracies
$1\sigma$
localisations for short GRBs can be obtained with accuracies
![]() $\lt 10$
’s of square degrees (e.g., Fermi GBM Goldstein et al. Reference Goldstein2020, the Neil Gehrels Swift Observatory Gehrels et al. Reference Gehrels2004; Troja Reference Troja2020, the Gravitational wave high-energy Electromagnetic Counterpart All-sky Monitor (GECAM; Zhao et al. Reference Zhao2021). To localise a substantial fraction of short GRBs to this accuracy with the current design of the HERMES instrument (and under the assumption that the satellites are uniformly distributed around equatorial and Polar orbits), at least 20 satellites divided evenly between equatorial and Polar orbit all observing the same field are required (i.e., combined detection from at least 10 HERMES instruments with large baselines in both the equatorial and Polar planes). On the other hand, the performance forecast for the localisation of long GRBs indicates that with an increase in the effective area of the detector, a constellation with a smaller number of elements would have a strong potential to provide state-of-the-art and cost effective all-sky monitoring and localisation of short GRBs/gravitational wave counterparts. A detailed investigation on the trade off between detector collecting area and number of constellation elements in the HERMES constellation is beyond the scope of this work (though the reader is directed to Greiner et al. Reference Greiner, Hugentobler, Burgess, Berlato, Rott and Tsvetkova2022, where a similar study for a hosted instrument on the Galileo constellation is presented).
$\lt 10$
’s of square degrees (e.g., Fermi GBM Goldstein et al. Reference Goldstein2020, the Neil Gehrels Swift Observatory Gehrels et al. Reference Gehrels2004; Troja Reference Troja2020, the Gravitational wave high-energy Electromagnetic Counterpart All-sky Monitor (GECAM; Zhao et al. Reference Zhao2021). To localise a substantial fraction of short GRBs to this accuracy with the current design of the HERMES instrument (and under the assumption that the satellites are uniformly distributed around equatorial and Polar orbits), at least 20 satellites divided evenly between equatorial and Polar orbit all observing the same field are required (i.e., combined detection from at least 10 HERMES instruments with large baselines in both the equatorial and Polar planes). On the other hand, the performance forecast for the localisation of long GRBs indicates that with an increase in the effective area of the detector, a constellation with a smaller number of elements would have a strong potential to provide state-of-the-art and cost effective all-sky monitoring and localisation of short GRBs/gravitational wave counterparts. A detailed investigation on the trade off between detector collecting area and number of constellation elements in the HERMES constellation is beyond the scope of this work (though the reader is directed to Greiner et al. Reference Greiner, Hugentobler, Burgess, Berlato, Rott and Tsvetkova2022, where a similar study for a hosted instrument on the Galileo constellation is presented).
6. Conclusion
In this paper we characterise the GRB localisation capabilities of the SpIRIT + HERMES-TP/SP mini-constellation using temporal triangulation techniques. We design a simplified mission simulation based on an optimised mission scenario for the HERMES-TP/SP outlined in Sanna et al. (Reference Sanna2020) and specific assumptions regarding SpIRIT’s orbit and pointing strategy in order to estimate the burst localisation capabilities of the combined constellation.
We find that the SpIRIT + HERMES-TP/SP constellation is able to localise 60% of long GRBs within a
![]() $1\sigma$
confidence region of 28 deg
$1\sigma$
confidence region of 28 deg
![]() $^2$
on the sky, and 90% of long GRBs within 150 deg
$^2$
on the sky, and 90% of long GRBs within 150 deg
![]() $^2$
. These confidence regions represent an improvement by a factor of
$^2$
. These confidence regions represent an improvement by a factor of
![]() ${\sim}$
5 over the HERMES-TP/SP alone and are comparable to the statistical burst localisation capabilities of the Fermi GBM (excluding systematic uncertainties for all satellites). The increased performance of SpIRIT + HERMES-TP/SP compared to HERMES-TP/SP alone is due to SpIRIT’s Polar orbit, which affords it a large baseline perpendicular to the equatorial orbit of the six HERMES-TP/SP satellites. We find that when SpIRIT is over the poles, the localisation capabilities of the combined constellation improve by a factor of
${\sim}$
5 over the HERMES-TP/SP alone and are comparable to the statistical burst localisation capabilities of the Fermi GBM (excluding systematic uncertainties for all satellites). The increased performance of SpIRIT + HERMES-TP/SP compared to HERMES-TP/SP alone is due to SpIRIT’s Polar orbit, which affords it a large baseline perpendicular to the equatorial orbit of the six HERMES-TP/SP satellites. We find that when SpIRIT is over the poles, the localisation capabilities of the combined constellation improve by a factor of
![]() ${\sim}$
5 compared to when SpIRIT is at the equator.
${\sim}$
5 compared to when SpIRIT is at the equator.
The short GRB localisation capabilities of SpIRIT + HERMES-TP/SP reflect a similar improvement by a factor of
![]() ${\sim}$
5 over HERMES-TP/SP alone, with the combined constellation localising 60% of short GRBs within
${\sim}$
5 over HERMES-TP/SP alone, with the combined constellation localising 60% of short GRBs within
![]() ${\sim}$
${\sim}$
![]() $1850$
deg
$1850$
deg
![]() $^2$
and 90% of short GRBs within
$^2$
and 90% of short GRBs within
![]() $6000$
deg
$6000$
deg
![]() $^2$
(1
$^2$
(1
![]() $\sigma$
confidence regions). In fact, for some faint short GRBs the constraint on the source’s position from statistical localisation techniques is so loose that constellation achieves more accurate GRB localisations when SpIRIT does not detect the burst, as this restricts the search region to the fraction of the sky that is obstructed by the Earth from SpIRIT’s perspective at the time of the burst. The short GRB localisation capabilities of the constellation is greatly reduced compared to long GRBs due to the limited precision in the signal cross-correlation between satellites, which could be addressed by increasing the collecting area of the HERMES instrument. While this forecast performance is not competitive with state-of-the-art localisation of Fermi GMB, the combined SpIRIT + HERMES-TP/SP is still expected to provide a meaningful contribution to multi-messenger astrophysics. This will be both for events that might be missed by Fermi due to Earth occultation, as well as through the unique time resolution of the HERMES instrument, which would enable novel investigation into rapid variability of the high-energy emission.
$\sigma$
confidence regions). In fact, for some faint short GRBs the constraint on the source’s position from statistical localisation techniques is so loose that constellation achieves more accurate GRB localisations when SpIRIT does not detect the burst, as this restricts the search region to the fraction of the sky that is obstructed by the Earth from SpIRIT’s perspective at the time of the burst. The short GRB localisation capabilities of the constellation is greatly reduced compared to long GRBs due to the limited precision in the signal cross-correlation between satellites, which could be addressed by increasing the collecting area of the HERMES instrument. While this forecast performance is not competitive with state-of-the-art localisation of Fermi GMB, the combined SpIRIT + HERMES-TP/SP is still expected to provide a meaningful contribution to multi-messenger astrophysics. This will be both for events that might be missed by Fermi due to Earth occultation, as well as through the unique time resolution of the HERMES instrument, which would enable novel investigation into rapid variability of the high-energy emission.
In order to further augment the capabilities of the HERMES-TP/SP, we investigated the localisation capabilities of an expanded nano-satellite constellation which includes additional satellites in Polar orbit. We find that a constellation covering two nearly orthogonal orbital planes comprising of 4 or 6 nano-satellites in each plane is capable of effectively localising 60% of long GRBs within
![]() ${\sim}$
5–10 deg
${\sim}$
5–10 deg
![]() $^2$
, and 60% of short GRBs to within
$^2$
, and 60% of short GRBs to within
![]() ${\sim}$
${\sim}$
![]() $550-850$
deg
$550-850$
deg
![]() $^2$
, which may enable an expanded nano-satellite constellation to aid in the timely localisation of bright short GRBs/GW transients. Furthermore, a constellation with 6 elements in Polar orbit enables 50% of long GRBs to be localised to within a statistical 68% uncertainty radius of
$^2$
, which may enable an expanded nano-satellite constellation to aid in the timely localisation of bright short GRBs/GW transients. Furthermore, a constellation with 6 elements in Polar orbit enables 50% of long GRBs to be localised to within a statistical 68% uncertainty radius of
![]() ${\sim}$
${\sim}$
![]() $1^{\circ}$
on the sky, which may enable systematic afterglow follow-up observations from future instruments with FoV’s
$1^{\circ}$
on the sky, which may enable systematic afterglow follow-up observations from future instruments with FoV’s
![]() ${\geq} 1$
deg
${\geq} 1$
deg
![]() $^2$
. Furthermore, it will be possible to integrate the expanded HERMES nano-satellite constellation into the IPN in order to achieve even more accurate sky localisations for both long and short GRBs, though this improved localisation would only be available at later times since the IPN latency can be substantial.
$^2$
. Furthermore, it will be possible to integrate the expanded HERMES nano-satellite constellation into the IPN in order to achieve even more accurate sky localisations for both long and short GRBs, though this improved localisation would only be available at later times since the IPN latency can be substantial.
Therefore, after successful on-orbit demonstration of the concept that is expected to be achieved by the SpIRIT + HERMES-TP/SP satellites, augmenting further the elements in Polar orbit would be an ideal next step towards achieving an all-sky X-ray/gamma-ray monitor based on distributed-aperture detectors to complement future gravitational wave detection campaigns.
Acknowledgements
MTh. acknowledges support from an Australian Government Research Training Program (RTP) Scholarship. This research is supported in part by the Australian Research Council Centre of Excellence for All-Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013. Parts of this research were supported by the Australian Research Council Centre of Excellence for Gravitational Wave Discovery (OzGrav), through project number CE170100004. GG acknowledges PRIN-MUR 2017 (grant 20179ZF5KS). JR acknowledges support by the European Union’s Horizon 2020 Programme under the AHEAD2020 project (grant agreement n. 871158).
Data Availability
Not applicable.