1. Introduction
The paper ‘Tandem droplet locomotion in a uniform electric field’ (Sorgentone & Vlahovska Reference Sorgentone and Vlahovska2022), referred to as Reference Sorgentone and VlahovskaSV in the following, studies the interaction of a dissimilar droplet pair in an electric field.
The interaction of complex fluids and electrical fields is at the heart of many phenomena in nature, e.g. rain drops in thunderstorms, as well as in technological applications, for instance electrospray, microfluidic applications like electrocoalescence or inkjet printing. Given today's state-of-the art industrial demands for precision engineering, the challenges to fluid dynamic modelling can indeed go down to the dynamics of the individual droplets, specifically considering net migration, coalescence or chaotic motion in multidroplet systems. An extensive review of the rich phenomenology spanning deformation, electrostreaming, breakup and electrorotation can be found in Vlahovska (Reference Vlahovska2019).
However, even the problem of two droplets in a moderate, uniform DC field is challenging, coupling charge and fluid dynamics in complex fluids with deformable interfaces. One needs to carefully choose the appropriate level of approximation in the modelling and choice of problem parameters, in order to have something tractable but not over-idealised beyond practical relevance, and eventually allowing for multidroplet frameworks.
The leaky dielectric model (Melcher & Taylor Reference Melcher and Taylor1969; Saville Reference Saville1997) is commonly used to treat weakly conducting multiphase fluids interacting with electric fields, providing governing equations to both analytical and numerical approaches. The key assumption is that the bulk medium can be considered as charge-free, such that electric and hydrodynamic fields are decoupled. The electrohydrodynamics of the system are then determined by the charge distribution in the interface and by the associated electrohydrodynamic (EHD) stresses, as well as by dielectrophoretic (DEP) forces. At typically low Reynolds numbers, the hydrodynamics can be treated as Stokesian.
Characteristic physical parameters for such dielectric emulsions are the ratios of permittivities,  $S$, conductivities,
$S$, conductivities,  $R$, and viscosities,
$R$, and viscosities,  $\lambda$, between droplet and bulk medium, and the electric capillary number
$\lambda$, between droplet and bulk medium, and the electric capillary number  $ {\textit {Ca}}$. For two-body interactions between dissimilar droplets
$ {\textit {Ca}}$. For two-body interactions between dissimilar droplets  $i$, individual quantities
$i$, individual quantities  $S_i$,
$S_i$,  $R_i$ and
$R_i$ and  $\lambda _i$ have to be considered, as well as the ratio of sizes.
$\lambda _i$ have to be considered, as well as the ratio of sizes.
In recent years, various analytical, numerical and experimental studies, with substantial contributions by Reference Sorgentone and VlahovskaSV and their collaborators, have approached the problem of such droplet–droplet interactions in a leaky dielectric framework. These typically include an asymptotic theory for the far-field interactions of widely separated droplets, given by a low-order electrohydrodynamic multipole expansion, while a more accurate expression for near-field interactions is provided by computationally more expensive boundary integral methods. The existing literature covers various degrees of complexity, starting from a pair of identical droplets at a distance  $d$, aligned with an electric field
$d$, aligned with an electric field  $E_0\hat {\boldsymbol{z}}$, such that
$E_0\hat {\boldsymbol{z}}$, such that  $\varTheta \equiv \arccos (\hat {\boldsymbol{d}}\boldsymbol {\cdot }\hat {\boldsymbol{z}})=0$ (Sozou Reference Sozou1975; Baygents, Rivette & Stone Reference Baygents, Rivette and Stone1998), over droplets dissimilar in
$\varTheta \equiv \arccos (\hat {\boldsymbol{d}}\boldsymbol {\cdot }\hat {\boldsymbol{z}})=0$ (Sozou Reference Sozou1975; Baygents, Rivette & Stone Reference Baygents, Rivette and Stone1998), over droplets dissimilar in  $S$,
$S$,  $R$,
$R$,  $\lambda$ and size, to arbitrary orientations (Sorgentone et al. Reference Sorgentone, Kach, Khair, Walker and Vlahovska2021), as well as including the effects of small deformations or surfactants (Sorgentone & Vlahovska Reference Sorgentone and Vlahovska2021). Kach, Walker & Khair (Reference Kach, Walker and Khair2022) proceed by applying the asymptotic theory to interactions between three, or, eventually, more droplets, and show an initial quantitative comparison with experiments.
$\lambda$ and size, to arbitrary orientations (Sorgentone et al. Reference Sorgentone, Kach, Khair, Walker and Vlahovska2021), as well as including the effects of small deformations or surfactants (Sorgentone & Vlahovska Reference Sorgentone and Vlahovska2021). Kach, Walker & Khair (Reference Kach, Walker and Khair2022) proceed by applying the asymptotic theory to interactions between three, or, eventually, more droplets, and show an initial quantitative comparison with experiments.
Now, Reference Sorgentone and VlahovskaSV, combining asymptotic theory and boundary integral numerics, provide a systematic investigation of the attractive or repulsive dynamics of dissimilar droplets depending on their initial alignment and distance in ( $d,\varTheta$) space. Intriguingly, they find a set of parameters where the droplets ‘swim’ steadily at a finite distance
$d,\varTheta$) space. Intriguingly, they find a set of parameters where the droplets ‘swim’ steadily at a finite distance  $d_{eq}$.
$d_{eq}$.
2. Overview
Generally, a single, charge-neutral drop in a uniform electric field does not move. For a pair of identical droplets, the centre of mass will not move, while the droplets may reorient around it, mutually attract, or repel. In contrast, dissimilar droplet pairs can translate, with a non-zero centre of mass velocity. The paper by Reference Sorgentone and VlahovskaSV now considers dissimilar droplet pairs, but with matching radii,  $a=1$, and viscosities, such that
$a=1$, and viscosities, such that  $\lambda _{1,2}=\lambda$. In consequence, DEP interactions, where the forces are reciprocal, do not contribute to centre of mass motion. They can still cause droplets to attract or repel depending on
$\lambda _{1,2}=\lambda$. In consequence, DEP interactions, where the forces are reciprocal, do not contribute to centre of mass motion. They can still cause droplets to attract or repel depending on  $\varTheta$, with a sign change at a critical angle
$\varTheta$, with a sign change at a critical angle  $\varTheta _c$. Additionally, the sign and magnitude of the DEP contribution to the velocities,
$\varTheta _c$. Additionally, the sign and magnitude of the DEP contribution to the velocities,  $\boldsymbol{U}_i^{DEP} (\beta _D, \lambda, \varTheta, d)$, which are opposed but equal, are controlled by the dipole strength
$\boldsymbol{U}_i^{DEP} (\beta _D, \lambda, \varTheta, d)$, which are opposed but equal, are controlled by the dipole strength  $\beta _D(R_1,R_2)$, which changes sign with
$\beta _D(R_1,R_2)$, which changes sign with  $(R_1-1)(R_2-1)$.
$(R_1-1)(R_2-1)$.
On the other hand, the contributions due to EHD interactions,  $\boldsymbol{U}_i^{EHD} (\beta _{T,i}, \lambda, \varTheta, d)$, depend on the strength of the EHD stresslets,
$\boldsymbol{U}_i^{EHD} (\beta _{T,i}, \lambda, \varTheta, d)$, depend on the strength of the EHD stresslets,  $\beta _{T,i}(R_i, S_i)$, which change sign with
$\beta _{T,i}(R_i, S_i)$, which change sign with  $R_i-S_i$, each. Thus, EHD interactions are in general non-reciprocal.
$R_i-S_i$, each. Thus, EHD interactions are in general non-reciprocal.
By an appropriate selection of  $R_i$ and
$R_i$ and  $S_i$, Reference Sorgentone and VlahovskaSV now find a state where the attractive and repulsive contributions of DEP and EHD interactions cancel, while still retaining a finite centre of mass speed
$S_i$, Reference Sorgentone and VlahovskaSV now find a state where the attractive and repulsive contributions of DEP and EHD interactions cancel, while still retaining a finite centre of mass speed  $\boldsymbol{U}_2-\boldsymbol{U}_1$, leading to steady pair motion at an equilibrium distance
$\boldsymbol{U}_2-\boldsymbol{U}_1$, leading to steady pair motion at an equilibrium distance  $s_{eq}$.
$s_{eq}$.
Then Reference Sorgentone and VlahovskaSV continue by mapping this dynamical system in  $(\varTheta,d)$ space via the time evolution of
$(\varTheta,d)$ space via the time evolution of  $\dot {\varTheta }$ and
$\dot {\varTheta }$ and  $\dot {d}$ for different initial values of
$\dot {d}$ for different initial values of  $\varTheta _0$ and
$\varTheta _0$ and  $d_0$. Figure 1(b) shows an example trajectory phase plane with
$d_0$. Figure 1(b) shows an example trajectory phase plane with  $d_{eq}=4.94$. There are two equilibrium points with separation
$d_{eq}=4.94$. There are two equilibrium points with separation  $d_{eq}$ at
$d_{eq}$ at  $\varTheta _{eq}$ of
$\varTheta _{eq}$ of  $0$ or
$0$ or  ${\rm \pi} /2$. The first is approached by starting from
${\rm \pi} /2$. The first is approached by starting from  $\varTheta _0=0$, with
$\varTheta _0=0$, with  $d$ evolving towards
$d$ evolving towards  $d_{eq}$ and the pair steadily continuing in the
$d_{eq}$ and the pair steadily continuing in the  $z$ direction. The second is found by starting with
$z$ direction. The second is found by starting with  $d$ already at
$d$ already at  $d_{eq}$, but arbitrary orientation, from where the pair is rotated towards
$d_{eq}$, but arbitrary orientation, from where the pair is rotated towards  $\varTheta ={\rm \pi} /2$, whereupon it moves on perpendicular to
$\varTheta ={\rm \pi} /2$, whereupon it moves on perpendicular to  $z$. Trajectories for all other initial values are unstable, ending in contact or infinite separation, depending solely on whether the initial separation
$z$. Trajectories for all other initial values are unstable, ending in contact or infinite separation, depending solely on whether the initial separation  $d_{0}$ is larger or smaller than
$d_{0}$ is larger or smaller than  $d_{eq}$. Figure 1(c) shows one such example starting at the point marked by a red star in figure 1(b), with
$d_{eq}$. Figure 1(c) shows one such example starting at the point marked by a red star in figure 1(b), with  $\varTheta _0=10^{\circ }$ and
$\varTheta _0=10^{\circ }$ and  $d_0=7$, where the droplets separate asymptotically after a transient approach and reorientation.
$d_0=7$, where the droplets separate asymptotically after a transient approach and reorientation.
Authors Reference Sorgentone and VlahovskaSV now analyse trajectories for two classes of either asymptotic parallel or antiparallel alignment with the field, discussing the cases of eventual approach or repulsion and singling out the contributions from DEP and EHD interactions. They compare, as shown by an example trajectory in figure 1(c), the predictions of the asymptotic theory with boundary integral simulation data that also account for deformation and near-field effects. Unsurprisingly, the asymptotic model is successful for wide separations and a good predictor for the asymptotic states of the droplet pair, but, quantitatively, it differs markedly in the dynamic time scales. Thus, it might be well worth the much higher computational cost (as evidenced by the limits of Reference Sorgentone and VlahovskaSV's simulations) when compared with experiments.
3. Outlook: should we look for a new active matter state?
The authors suggest, beyond technical applications like droplet sorting, that the motile paired state could inspire new designs of active units. Usually, experimental microswimmer realisations (Figure 2) depend on the conversion of a chemical fuel, i.e. undirected, molecular-scale energy, into directed mesoscopic motion. Many systems are in a sense limited by the depletion of fuel and complicated by its transport, and therefore lack a long-time thermodynamically steady state. One notable example of theoretically unlimited external actuation are the light-driven colloidal swimmers of Buttinoni et al. (Reference Buttinoni, Volpe, Kümmel, Volpe and Bechinger2012). Fuelling the motion via an external electric field, as suggested here, is an attractive idea, which has already seen a popular realisation in the form of Quincke colloidal rollers (Bricard et al. Reference Bricard, Caussin, Desreumaux, Dauchot and Bartolo2013). Authors Reference Sorgentone and VlahovskaSV identify two modes of stable pair motion, parallel and perpendicular to the field. The parallel one is strictly tied to the field direction, and therefore could not be called truly autonomous. However, the parallel one has a freedom in two dimensions equivalent to that of Quincke rollers, does not require a boundary to roll on and is fully fluid based.
The major practical challenge would be that active matter tends to thrive on fluctuations, chaos and interactions with its environment, to which the delicate balance of the droplet pair is highly vulnerable due to the saddle-point character of the equilibrium points. In practice, any distance fluctuation would drive the pair towards contact or separation and it will need some ingenuity on the experimental side to stabilise it.
The closest existing analogues among microswimmers could be the paired and ‘waltzing’ states between two interacting chemotactic swimmers in Saha, Ramaswamy & Golestanian (Reference Saha, Ramaswamy and Golestanian2019), or the ‘predator–prey’ dynamics between dissimilar active droplets in Meredith et al. (Reference Meredith, Moerman, Groenewold, Chiu, Kegel, van Blaaderen and Zarzar2020). However, as opposed to Reference Sorgentone and VlahovskaSV's tandem swimmers, these systems are able to propel individually and do not have to form a pair to propel. One should further note that the pairs in Meredith et al. (Reference Meredith, Moerman, Groenewold, Chiu, Kegel, van Blaaderen and Zarzar2020) will always end up in contact. Similarly, the trajectory discussion in figure 4 of Reference Sorgentone and VlahovskaSV suggests that droplets approaching contact still have a finite centre of mass speed. Since dissimilar droplets could also be chosen to be immiscible, could not even an unstable pair continue to move as an electrohydrodynamically driven compound swimmer?
A final question would be whether such bound states are possible in multidroplet emulsions. Authors Reference Sorgentone and VlahovskaSV have already hinted at the capability of their fully three-dimensional boundary integral method to simulate many droplets at arbitrary field alignment, and it seems an excellent prospect for future studies.
Figure 2. Comparison with existing microswimmer paradigms: (a) The tandem swimmers proposed by Sorgentone & Vlahovska (Reference Sorgentone and Vlahovska2022), (b) a light-powered Janus colloid based on the local separation of a critical mixture, after Buttinoni et al. (Reference Buttinoni, Volpe, Kümmel, Volpe and Bechinger2012), (c) a Quincke roller, driven by an external electric field, as in Bricard et al. (Reference Bricard, Caussin, Desreumaux, Dauchot and Bartolo2013), and (d) ‘predator–prey’ Marangoni swimmers, powered by micellar solute transport between two droplets, after Meredith et al. (Reference Meredith, Moerman, Groenewold, Chiu, Kegel, van Blaaderen and Zarzar2020).

 $z$. (b) Phase plane of droplet trajectories with
$z$. (b) Phase plane of droplet trajectories with  $R_1=0.1$,
$R_1=0.1$,  $R_2=100$,
$R_2=100$,  $S_1=S_2=1$. (c) Example trajectories for two droplets with
$S_1=S_2=1$. (c) Example trajectories for two droplets with  $R_1=0.1$ (red),
$R_1=0.1$ (red),  $R_2=100$ (blue),
$R_2=100$ (blue),  $S_1=S_2=1$, starting at
$S_1=S_2=1$, starting at  $\varTheta _0=10^{\circ }$,
$\varTheta _0=10^{\circ }$,  $d_0=7$ (see * in b); thin lines denote asymptotic theory, thick lines simulations. Figure adapted from Sorgentone & Vlahovska (2022).
$d_0=7$ (see * in b); thin lines denote asymptotic theory, thick lines simulations. Figure adapted from Sorgentone & Vlahovska (2022).




1. Introduction
The paper ‘Tandem droplet locomotion in a uniform electric field’ (Sorgentone & Vlahovska Reference Sorgentone and Vlahovska2022), referred to as Reference Sorgentone and VlahovskaSV in the following, studies the interaction of a dissimilar droplet pair in an electric field.
The interaction of complex fluids and electrical fields is at the heart of many phenomena in nature, e.g. rain drops in thunderstorms, as well as in technological applications, for instance electrospray, microfluidic applications like electrocoalescence or inkjet printing. Given today's state-of-the art industrial demands for precision engineering, the challenges to fluid dynamic modelling can indeed go down to the dynamics of the individual droplets, specifically considering net migration, coalescence or chaotic motion in multidroplet systems. An extensive review of the rich phenomenology spanning deformation, electrostreaming, breakup and electrorotation can be found in Vlahovska (Reference Vlahovska2019).
However, even the problem of two droplets in a moderate, uniform DC field is challenging, coupling charge and fluid dynamics in complex fluids with deformable interfaces. One needs to carefully choose the appropriate level of approximation in the modelling and choice of problem parameters, in order to have something tractable but not over-idealised beyond practical relevance, and eventually allowing for multidroplet frameworks.
The leaky dielectric model (Melcher & Taylor Reference Melcher and Taylor1969; Saville Reference Saville1997) is commonly used to treat weakly conducting multiphase fluids interacting with electric fields, providing governing equations to both analytical and numerical approaches. The key assumption is that the bulk medium can be considered as charge-free, such that electric and hydrodynamic fields are decoupled. The electrohydrodynamics of the system are then determined by the charge distribution in the interface and by the associated electrohydrodynamic (EHD) stresses, as well as by dielectrophoretic (DEP) forces. At typically low Reynolds numbers, the hydrodynamics can be treated as Stokesian.
Characteristic physical parameters for such dielectric emulsions are the ratios of permittivities, $S$, conductivities,
$S$, conductivities,  $R$, and viscosities,
$R$, and viscosities,  $\lambda$, between droplet and bulk medium, and the electric capillary number
$\lambda$, between droplet and bulk medium, and the electric capillary number  $ {\textit {Ca}}$. For two-body interactions between dissimilar droplets
$ {\textit {Ca}}$. For two-body interactions between dissimilar droplets  $i$, individual quantities
$i$, individual quantities  $S_i$,
$S_i$,  $R_i$ and
$R_i$ and  $\lambda _i$ have to be considered, as well as the ratio of sizes.
$\lambda _i$ have to be considered, as well as the ratio of sizes.
In recent years, various analytical, numerical and experimental studies, with substantial contributions by Reference Sorgentone and VlahovskaSV and their collaborators, have approached the problem of such droplet–droplet interactions in a leaky dielectric framework. These typically include an asymptotic theory for the far-field interactions of widely separated droplets, given by a low-order electrohydrodynamic multipole expansion, while a more accurate expression for near-field interactions is provided by computationally more expensive boundary integral methods. The existing literature covers various degrees of complexity, starting from a pair of identical droplets at a distance $d$, aligned with an electric field
$d$, aligned with an electric field  $E_0\hat {\boldsymbol{z}}$, such that
$E_0\hat {\boldsymbol{z}}$, such that  $\varTheta \equiv \arccos (\hat {\boldsymbol{d}}\boldsymbol {\cdot }\hat {\boldsymbol{z}})=0$ (Sozou Reference Sozou1975; Baygents, Rivette & Stone Reference Baygents, Rivette and Stone1998), over droplets dissimilar in
$\varTheta \equiv \arccos (\hat {\boldsymbol{d}}\boldsymbol {\cdot }\hat {\boldsymbol{z}})=0$ (Sozou Reference Sozou1975; Baygents, Rivette & Stone Reference Baygents, Rivette and Stone1998), over droplets dissimilar in  $S$,
$S$,  $R$,
$R$,  $\lambda$ and size, to arbitrary orientations (Sorgentone et al. Reference Sorgentone, Kach, Khair, Walker and Vlahovska2021), as well as including the effects of small deformations or surfactants (Sorgentone & Vlahovska Reference Sorgentone and Vlahovska2021). Kach, Walker & Khair (Reference Kach, Walker and Khair2022) proceed by applying the asymptotic theory to interactions between three, or, eventually, more droplets, and show an initial quantitative comparison with experiments.
$\lambda$ and size, to arbitrary orientations (Sorgentone et al. Reference Sorgentone, Kach, Khair, Walker and Vlahovska2021), as well as including the effects of small deformations or surfactants (Sorgentone & Vlahovska Reference Sorgentone and Vlahovska2021). Kach, Walker & Khair (Reference Kach, Walker and Khair2022) proceed by applying the asymptotic theory to interactions between three, or, eventually, more droplets, and show an initial quantitative comparison with experiments.
Now, Reference Sorgentone and VlahovskaSV, combining asymptotic theory and boundary integral numerics, provide a systematic investigation of the attractive or repulsive dynamics of dissimilar droplets depending on their initial alignment and distance in ( $d,\varTheta$) space. Intriguingly, they find a set of parameters where the droplets ‘swim’ steadily at a finite distance
$d,\varTheta$) space. Intriguingly, they find a set of parameters where the droplets ‘swim’ steadily at a finite distance  $d_{eq}$.
$d_{eq}$.
2. Overview
Generally, a single, charge-neutral drop in a uniform electric field does not move. For a pair of identical droplets, the centre of mass will not move, while the droplets may reorient around it, mutually attract, or repel. In contrast, dissimilar droplet pairs can translate, with a non-zero centre of mass velocity. The paper by Reference Sorgentone and VlahovskaSV now considers dissimilar droplet pairs, but with matching radii, $a=1$, and viscosities, such that
$a=1$, and viscosities, such that  $\lambda _{1,2}=\lambda$. In consequence, DEP interactions, where the forces are reciprocal, do not contribute to centre of mass motion. They can still cause droplets to attract or repel depending on
$\lambda _{1,2}=\lambda$. In consequence, DEP interactions, where the forces are reciprocal, do not contribute to centre of mass motion. They can still cause droplets to attract or repel depending on  $\varTheta$, with a sign change at a critical angle
$\varTheta$, with a sign change at a critical angle  $\varTheta _c$. Additionally, the sign and magnitude of the DEP contribution to the velocities,
$\varTheta _c$. Additionally, the sign and magnitude of the DEP contribution to the velocities,  $\boldsymbol{U}_i^{DEP} (\beta _D, \lambda, \varTheta, d)$, which are opposed but equal, are controlled by the dipole strength
$\boldsymbol{U}_i^{DEP} (\beta _D, \lambda, \varTheta, d)$, which are opposed but equal, are controlled by the dipole strength  $\beta _D(R_1,R_2)$, which changes sign with
$\beta _D(R_1,R_2)$, which changes sign with  $(R_1-1)(R_2-1)$.
$(R_1-1)(R_2-1)$.
On the other hand, the contributions due to EHD interactions, $\boldsymbol{U}_i^{EHD} (\beta _{T,i}, \lambda, \varTheta, d)$, depend on the strength of the EHD stresslets,
$\boldsymbol{U}_i^{EHD} (\beta _{T,i}, \lambda, \varTheta, d)$, depend on the strength of the EHD stresslets,  $\beta _{T,i}(R_i, S_i)$, which change sign with
$\beta _{T,i}(R_i, S_i)$, which change sign with  $R_i-S_i$, each. Thus, EHD interactions are in general non-reciprocal.
$R_i-S_i$, each. Thus, EHD interactions are in general non-reciprocal.
By an appropriate selection of $R_i$ and
$R_i$ and  $S_i$, Reference Sorgentone and VlahovskaSV now find a state where the attractive and repulsive contributions of DEP and EHD interactions cancel, while still retaining a finite centre of mass speed
$S_i$, Reference Sorgentone and VlahovskaSV now find a state where the attractive and repulsive contributions of DEP and EHD interactions cancel, while still retaining a finite centre of mass speed  $\boldsymbol{U}_2-\boldsymbol{U}_1$, leading to steady pair motion at an equilibrium distance
$\boldsymbol{U}_2-\boldsymbol{U}_1$, leading to steady pair motion at an equilibrium distance  $s_{eq}$.
$s_{eq}$.
Then Reference Sorgentone and VlahovskaSV continue by mapping this dynamical system in $(\varTheta,d)$ space via the time evolution of
$(\varTheta,d)$ space via the time evolution of  $\dot {\varTheta }$ and
$\dot {\varTheta }$ and  $\dot {d}$ for different initial values of
$\dot {d}$ for different initial values of  $\varTheta _0$ and
$\varTheta _0$ and  $d_0$. Figure 1(b) shows an example trajectory phase plane with
$d_0$. Figure 1(b) shows an example trajectory phase plane with  $d_{eq}=4.94$. There are two equilibrium points with separation
$d_{eq}=4.94$. There are two equilibrium points with separation  $d_{eq}$ at
$d_{eq}$ at  $\varTheta _{eq}$ of
$\varTheta _{eq}$ of  $0$ or
$0$ or  ${\rm \pi} /2$. The first is approached by starting from
${\rm \pi} /2$. The first is approached by starting from  $\varTheta _0=0$, with
$\varTheta _0=0$, with  $d$ evolving towards
$d$ evolving towards  $d_{eq}$ and the pair steadily continuing in the
$d_{eq}$ and the pair steadily continuing in the  $z$ direction. The second is found by starting with
$z$ direction. The second is found by starting with  $d$ already at
$d$ already at  $d_{eq}$, but arbitrary orientation, from where the pair is rotated towards
$d_{eq}$, but arbitrary orientation, from where the pair is rotated towards  $\varTheta ={\rm \pi} /2$, whereupon it moves on perpendicular to
$\varTheta ={\rm \pi} /2$, whereupon it moves on perpendicular to  $z$. Trajectories for all other initial values are unstable, ending in contact or infinite separation, depending solely on whether the initial separation
$z$. Trajectories for all other initial values are unstable, ending in contact or infinite separation, depending solely on whether the initial separation  $d_{0}$ is larger or smaller than
$d_{0}$ is larger or smaller than  $d_{eq}$. Figure 1(c) shows one such example starting at the point marked by a red star in figure 1(b), with
$d_{eq}$. Figure 1(c) shows one such example starting at the point marked by a red star in figure 1(b), with  $\varTheta _0=10^{\circ }$ and
$\varTheta _0=10^{\circ }$ and  $d_0=7$, where the droplets separate asymptotically after a transient approach and reorientation.
$d_0=7$, where the droplets separate asymptotically after a transient approach and reorientation.
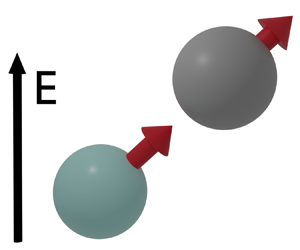
Figure 1. (a) Problem geometry of two dissimilar droplets suspended in a fluid in an electric field in $z$. (b) Phase plane of droplet trajectories with
$z$. (b) Phase plane of droplet trajectories with  $R_1=0.1$,
$R_1=0.1$,  $R_2=100$,
$R_2=100$,  $S_1=S_2=1$. (c) Example trajectories for two droplets with
$S_1=S_2=1$. (c) Example trajectories for two droplets with  $R_1=0.1$ (red),
$R_1=0.1$ (red),  $R_2=100$ (blue),
$R_2=100$ (blue),  $S_1=S_2=1$, starting at
$S_1=S_2=1$, starting at  $\varTheta _0=10^{\circ }$,
$\varTheta _0=10^{\circ }$,  $d_0=7$ (see * in b); thin lines denote asymptotic theory, thick lines simulations. Figure adapted from Sorgentone & Vlahovska (Reference Sorgentone and Vlahovska2022).
$d_0=7$ (see * in b); thin lines denote asymptotic theory, thick lines simulations. Figure adapted from Sorgentone & Vlahovska (Reference Sorgentone and Vlahovska2022).
Authors Reference Sorgentone and VlahovskaSV now analyse trajectories for two classes of either asymptotic parallel or antiparallel alignment with the field, discussing the cases of eventual approach or repulsion and singling out the contributions from DEP and EHD interactions. They compare, as shown by an example trajectory in figure 1(c), the predictions of the asymptotic theory with boundary integral simulation data that also account for deformation and near-field effects. Unsurprisingly, the asymptotic model is successful for wide separations and a good predictor for the asymptotic states of the droplet pair, but, quantitatively, it differs markedly in the dynamic time scales. Thus, it might be well worth the much higher computational cost (as evidenced by the limits of Reference Sorgentone and VlahovskaSV's simulations) when compared with experiments.
3. Outlook: should we look for a new active matter state?
The authors suggest, beyond technical applications like droplet sorting, that the motile paired state could inspire new designs of active units. Usually, experimental microswimmer realisations (Figure 2) depend on the conversion of a chemical fuel, i.e. undirected, molecular-scale energy, into directed mesoscopic motion. Many systems are in a sense limited by the depletion of fuel and complicated by its transport, and therefore lack a long-time thermodynamically steady state. One notable example of theoretically unlimited external actuation are the light-driven colloidal swimmers of Buttinoni et al. (Reference Buttinoni, Volpe, Kümmel, Volpe and Bechinger2012). Fuelling the motion via an external electric field, as suggested here, is an attractive idea, which has already seen a popular realisation in the form of Quincke colloidal rollers (Bricard et al. Reference Bricard, Caussin, Desreumaux, Dauchot and Bartolo2013). Authors Reference Sorgentone and VlahovskaSV identify two modes of stable pair motion, parallel and perpendicular to the field. The parallel one is strictly tied to the field direction, and therefore could not be called truly autonomous. However, the parallel one has a freedom in two dimensions equivalent to that of Quincke rollers, does not require a boundary to roll on and is fully fluid based.
The major practical challenge would be that active matter tends to thrive on fluctuations, chaos and interactions with its environment, to which the delicate balance of the droplet pair is highly vulnerable due to the saddle-point character of the equilibrium points. In practice, any distance fluctuation would drive the pair towards contact or separation and it will need some ingenuity on the experimental side to stabilise it.
The closest existing analogues among microswimmers could be the paired and ‘waltzing’ states between two interacting chemotactic swimmers in Saha, Ramaswamy & Golestanian (Reference Saha, Ramaswamy and Golestanian2019), or the ‘predator–prey’ dynamics between dissimilar active droplets in Meredith et al. (Reference Meredith, Moerman, Groenewold, Chiu, Kegel, van Blaaderen and Zarzar2020). However, as opposed to Reference Sorgentone and VlahovskaSV's tandem swimmers, these systems are able to propel individually and do not have to form a pair to propel. One should further note that the pairs in Meredith et al. (Reference Meredith, Moerman, Groenewold, Chiu, Kegel, van Blaaderen and Zarzar2020) will always end up in contact. Similarly, the trajectory discussion in figure 4 of Reference Sorgentone and VlahovskaSV suggests that droplets approaching contact still have a finite centre of mass speed. Since dissimilar droplets could also be chosen to be immiscible, could not even an unstable pair continue to move as an electrohydrodynamically driven compound swimmer?
A final question would be whether such bound states are possible in multidroplet emulsions. Authors Reference Sorgentone and VlahovskaSV have already hinted at the capability of their fully three-dimensional boundary integral method to simulate many droplets at arbitrary field alignment, and it seems an excellent prospect for future studies.
Figure 2. Comparison with existing microswimmer paradigms: (a) The tandem swimmers proposed by Sorgentone & Vlahovska (Reference Sorgentone and Vlahovska2022), (b) a light-powered Janus colloid based on the local separation of a critical mixture, after Buttinoni et al. (Reference Buttinoni, Volpe, Kümmel, Volpe and Bechinger2012), (c) a Quincke roller, driven by an external electric field, as in Bricard et al. (Reference Bricard, Caussin, Desreumaux, Dauchot and Bartolo2013), and (d) ‘predator–prey’ Marangoni swimmers, powered by micellar solute transport between two droplets, after Meredith et al. (Reference Meredith, Moerman, Groenewold, Chiu, Kegel, van Blaaderen and Zarzar2020).
Declaration of interests
The author reports no conflict of interest.