Terminology

To avoid confusion, we define the meanings of our terms:

• • Unit/individual – an entity, such as an object, person, or culture. We will use the term ‘individual’ instead of the more general term ‘unit’. Think ‘row’ in a dataset.

• • Variable – a feature of an individual, transient or permanent. For example, ‘Albert was sleepy but is no longer’ or ‘Alice was born 30 November’.

• • Treatment – equivalent to ‘exposure’, an event that might change a variable. For instance, ‘Albert was sleepy; we intervened with coffee; he is now wide awake’ or ‘Alice was born in November; nothing can change that’.

• • Outcome – the response variable or ‘effect’. In causal inference, we contrast ‘potential’ or ‘counterfactual outcomes’. In observational or ‘real-world’ studies where treatments are not randomised, the assumptions for obtaining contrasts of counterfactual outcomes are typically much stronger than in randomised controlled experiments.

• • Confounding – a state where the treatment and outcome share a common cause and no adjustment is made to remove the non-causal association, or where the treatment and outcome share a common effect, and adjustment is made for this common effect, or when the effect of the treatment on the outcome is mediated by a variable which is conditioned upon. In each case, the observed association will not reflect a causal association. Causal directed acyclic graphs clarify strategies for confounding control.

• • Measurement – a recorded trace of a variable, such as a column in a dataset. When placing measurements within causal settings, we call measurements reporters.

• • Measurement error – a misalignment between the true state of a variable and its reported state. For example, ‘Alice was born on 30 November; records were lost, and her birthday was recorded as 1 December’.

• • Population – an abstraction from statistics, denoting the set of all individuals defined by certain features. Albert belongs to the set of all individuals who ignore instructions.

• • Super-population – an abstraction, the population of all possible individuals of a given kind. Albert and Alice belong to a super-population of hominins.

• • Restricted population – population p is restricted relative to another population P if the individuals p ∈ P share some but not all features of P. ‘The living’ is a restriction of hominins.

• • Target population – a restriction of the super-population whose features interest investigators. An investigator who defines their interests is a member of the population of ‘good investigators’.

• • Source population – the population from which the study's sample is drawn. Investigators wanted to recruit from a general population but recruited from the pool of first-year university psychology students.

• • Sample population at baseline – or equivalently the ‘analytical sample population.’ The abstract set of individuals from which the units in a study at treatment assignment belong, e.g. ‘the set of all first-year university psychology students who might end up in this study’. Unless stated otherwise, we will consider the baseline analytic sample population to represent the source population; we will consider the analytic population at baseline to be representative of the target population.

• • Selection into the analytic sample – selection occurs and is under investigator control when a target population is defined from a super-population or when investigators apply eligibility criteria for inclusion in the analytic sample. Selection into the sample is often out of the investigator's control. Investigators might aspire to answer questions about all of humanity but find themselves limited to undergraduate samples. Investigators might sample from a source population but recover an analytic sample that differs from it in ways they cannot measure, such as mistrust of scientists. There is typically attrition of an analytic sample over time, and this is not typically fully within investigator control. Because the term ‘selection’ has different meanings in different areas of human science, we will speak of ‘target population restriction at the start of study’. Note that to evaluate this bias, it is important for investigators to state a causal effect of interest with respect to the full data that include the counterfactual quantities for the treatments to be compared in a clearly defined target population where all members of the target population are exposed to each level of treatment to be contrasted (Lu et al., Reference Lu, Cole, Howe and Westreich2022; Westreich et al., Reference Westreich, Edwards, Lesko, Stuart and Cole2017).

• • (Right) censored analytic sample at the end of study – right censoring is generally uninformative if there is no treatment effect for everyone in the baseline population (the sharp causal null hypothesis). Censoring is informative if there is an effect of the treatment, and this effect varies in at least one stratum of the baseline population (Hernán, Reference Hernán2017). If no correction is applied, unbiased effect estimates for the analytic sample will bias causal effect estimates for the target population in at least one measure of effect (Greenland, Reference Greenland2009; Lash et al., Reference Lash, Rothman, VanderWeele and Haneuse2020; VanderWeele, Reference VanderWeele2012). We call such bias from right censoring ‘target population restriction at the end of study’. Note again that to evaluate this bias, the causal effect of interest must be stated with respect to the full data that includes the counterfactual quantities for the treatments to be compared in a clearly defined target population where all members of the target population are exposed to each level of treatment to be contrasted (Westreich et al., Reference Westreich, Edwards, Lesko, Stuart and Cole2017).

• • Target population restriction bias – bias occurs when the distribution of effect modifiers in the analytic sample population differs from that in the target population, at the start, at the end, or throughout the study. Here we consider target population restriction bias at the start of study and target population restriction bias at the end of study. If this bias occurs at the start of the study, it will generally occur at the end of the study (and at intervals between), except by accident. We require validity to be non-accidental.

• • Generalisability – a study's findings generalise to a target population if the effects observed in the analytic sample at the end of study are also valid for the target population for structurally valid reasons (i.e. non-accidentally).

• • Transportability – when the analytic sample is not drawn from the target population, we cannot directly generalise the findings. However, we can transport the estimated causal effect from the source population to the target population under certain assumptions. This involves adjusting for differences in the distributions of effect modifiers between the two populations. The closer the source population is to the target population, the more plausible the transportability assumptions and the less we need to rely on complex adjustment methods see (Refer to supplementary materials S2).

• • Marginal effect – typically a synonym for the average treatment effect – always relative to some population specified by investigators.

• • Intention-to-treat effect – the marginal effect of random treatment assignment.

• • Per-protocol effect – the effect of adherence to a randomly assigned treatment if adherence was perfect (Hernán & Robins Reference Hernán and Robins2017). We have no guarantee that the intention-to-treat effect will be the same as the per-protocol effect. A safe assumption is that:

  $$\widehat{{ATE}}_{{\rm target}}^{{\rm Per}\hbox{-}{\rm Protocol}} \ne \widehat{{ATE}}_{{\rm target}}^{{\rm Intention}\hbox{-}{\rm to}\hbox{-}{\rm Treat}} $$

When evaluating evidence for causality, in addition to specifying their causal contrast, effect measure and target population, investigators should specify whether they are estimating an intention-to-treat or per-protocol effect (Hernán, Reference Hernán2004; Tripepi et al., Reference Tripepi, Jager, Dekker, Wanner and Zoccali2007).

• • WEIRD – a sample of ‘western, educated, industrialised, rich, and democratic societies’ (Henrich et al., Reference Henrich, Heine and Norenzayan2010).

• • weird (wrongly estimated inferences owing to inappropriate restriction and distortion) – a causal effect estimate that is not valid for the target population, either from confounding bias, measurement error bias, target population restriction at the start of study, or target population restriction at the end of study.

For discussion of these concepts refer to Dahabreh et al. (Reference Dahabreh, Haneuse, Robins, Robertson, Buchanan, Stuart and Hernán2021), Imai et al. (Reference Imai, King and Stuart2008), Cole and Stuart (Reference Cole and Stuart2010) and Westreich et al. (Reference Westreich, Edwards, Lesko, Stuart and Cole2017). A clear decomposition of key concepts needed to external validity – or what we call ‘target validity’ – is given in Imai et al. (Reference Imai, King and Stuart2008). For a less technical, pragmatically useful discussion, refer to Stuart et al. (Reference Stuart, Ackerman and Westreich2018). Note that terminology differs across the causal inference literature. See supplementary materials S1 for a causal inference glossary.

Graphical conventions

• • A – denotes the ‘treatment’ or ‘exposure’, a random variable, ‘the cause’.

• • Y – denotes the outcome or response, measured at the end of the study. Y is the ‘effect’.

• • L – denotes a measured confounder or set of confounders.

• • U – denotes an unmeasured confounder or confounders.

• • R – denotes randomisation to treatment condition $( {\cal R}\to A)$.

• • Node – denotes characteristics or features of units within a population on a causal diagram, that is, a ‘variable’. In causal directed acyclic graphs, nodes are drawn with respect to the target population, which is the population for whom investigators seek causal inferences (Suzuki et al., Reference Suzuki, Shinozaki and Yamamoto2020). Time-indexed nodes: X _t denotes relative chronology.

• • Edge without an Arrow () – path of association, causality not asserted.

• • Red edge without an arrow () – Confounding path, ignoring arrows to clarify statistical dependencies.

• • Arrow (→) – denotes a causal relationship from the node at the base of the arrow (a ‘parent’) to the node at the tip of the arrow (a ‘child’). In causal directed acyclic graphs, it is conventional to refrain from drawing an arrow from treatment to outcome to avoid asserting a causal path from A to Y because we aim to ascertain whether causality can be identified for this path. All other nodes and paths – including the absence of nodes and paths – are typically assumed.

• • Red arrow () – denotes a path of non-causal association between the treatment and outcome. Despite the arrows, this path is associational and may flow against time.

• • Open blue arrow () – denotes effect modification, which occurs when the effect of treatment varies within levels of a covariate. We do not assess the causal effect of the effect modifier on the outcome, recognising that it may be incoherent to consider intervening on the effect modifier. However, if the distribution of effect modifiers in the analytic sample population differs from that in the target population, then at least one measure of causal effect will differ between the two populations.

• • Boxed variable ()– denotes conditioning or adjustment for X.

• • Red-boxed variable () – highlights the source of confounding bias from adjustment.

• • Dashed circle () – denotes no adjustment is made for a variable (implied for unmeasured confounders).

• • G – names a causal diagram.

• • Split node (SWIGs) () – convention used in single world intervention graphs (SWIGs) that allows for factorisation of counterfactuals by splitting a node at an intervention with post-intervention nodes relabelled to match the treatment. We introduce single world intervention graphs in Part 4.

• • Unobserved node (SWIGs) () – our convention when using single world intervention graphs to denote an unobserved node (SWIGs): X unmeasured.

Causal directed acyclic graphs (DAGs)

Judea Pearl proved that, based on assumptions about causal structure, researchers can identify causal effects from joint distributions of observed data (Pearl, Reference Pearl1995, Reference Pearl2009). The rules of d-separation are given in Table 1.

Table 1. Five elementary causal structures in a causal directed acyclic graph

Key: , a directed edge, denotes causal association. The absence of an arrow denotes no causal association. Rules of d-separation: In a causal diagram, a path is ‘blocked’ or ‘d-separated’ if a node along it interrupts causation. Two variables are d-separated if all paths connecting them are blocked or if there are no paths linking them, making them conditionally independent. Conversely, unblocked paths result in ‘d-connected’ variables, implying statistical association. Refer to Pearl (Reference Pearl1995).

Note that ‘d’ stands for ‘directional’.

Implication: $ {\cal G} $ denotes a causal directed acyclic graph (causal DAG). P denotes a probability distribution function. Pearl proved that independence in a causal DAG $( B\coprod C\vert A)_{\cal G} $ implies probabilistic independence $B\coprod C\vert A$)_P; likewise if ($B\coprod C\vert A$)_P holds in all distributions compatible with $ {\cal G} $, it follows that ($B\coprod C\vert A$)_G (refer to Pearl Reference Pearl2009, p.61.) We read causal graphs to understand the implications of causality for relationships in observable data. However, reading causal structures from data is more challenging because the relationships in observable data are typically compatible with more than one (and typically many) causal graphs.

Pearl's rules of d-separation can be stated as follows:

• • Fork rule () –B and C are independent when conditioned on A ($B\coprod C{\rm \mid }A$).

• • Chain rule () – conditioning on B blocks the path between A and C ($A\coprod C{\rm \mid }B$).

• • Collider rule ()–A and B are independent until conditioned on C, which introduces dependence .

Table 1 shows causal directed acyclic graphs corresponding to these rules. Because all causal relationships can be assembled from combinations of the five structures presented in Table 1, we can use causal graphs to evaluate whether and how causal effects may be identified from data (Bulbulia, Reference Bulbulia2024b).

Pearl's general identification algorithm is known as the ‘back door adjustment theorem’ (Pearl, Reference Pearl2009).

Example 1: uncorrelated non-differential errors under sharp null – no treatment effect

Table 3 G ₁ illustrates uncorrelated non-differential measurement error under the ‘sharp-null,’ which arises when the error terms in the exposure and outcome are independent. In this setting, the measurement error structure is not expected to produce bias.

For example, consider a study investigating the causal effect of beliefs in big Gods on social complexity in ancient societies. Imagine that societies either randomly omitted or inaccurately recorded details about their beliefs in big Gods and their social complexities. This might occur because of varying preservation in the records of cultures which is unrelated to the actual beliefs or social complexity. In this scenario, we imagine the errors in historical records for beliefs in big Gods and for social complexity are independent. When the treatment is randomised, uncorrelated and undirected errors will generally not introduce bias under the sharp null of no treatment effect for any unit when all backdoor paths are closed. However, if confounders are measured without error this may open a backdoor path from treatment to outcome. For example, Robins and Hernán (Reference Robins and Hernán2008: 2216) discuss how in non-experimental settings, mismeasured confounders can introduce bias even when the measurement errors of the treatment and outcome are uncorrelated and undirected and there is no treatment effect. This is because mismeasured confounders will not control for confounding bias. We present an illustration of this bias in Table 6, G_3 where we discuss challenges to comparative research in which the accuracy of confounder measurements varies across the sites to be compared.

Example 2: uncorrelated non-differential errors ‘off the null’ (true treatment effect) biases true effects towards the null

Table 3 G ₂ illustrates uncorrelated non-differential measurement error, which arises when the error terms in the exposure and outcome are independent This bias is also called information bias (Lash et al., Reference Lash, Fox and Fink2009). In this setting, bias will often attenuate a true treatment effect. However, there are no guarantees that uncorrelated undirected measurement error biases effect estimates towards the null (Jurek et al., Reference Jurek, Greenland, Maldonado and Church2005, Reference Jurek, Maldonado, Greenland and Church2006, Reference Jurek, Greenland and Maldonado2008; Lash et al., Reference Lash, Fox and Fink2009: 93).

Consider again the example of a study investigating a causal effect of beliefs in big Gods on social complexity in ancient societies, where there are uncorrelated errors in the treatment and outcome. In this case, measurement error will often make it seem that the true causal effects of beliefs in big Gods are smaller than they are, or perhaps even that such an effect is absent. Often but not always: again, attenuation of the effect estimate is not guaranteed, and mismeasured confounders will open backdoor paths. We can, however, say this: uncorrelated undirected measurement error in the presence of a true effect leads to distortion of that effect, inviting weird results (wrongly estimated inferences owing to inappropriate restriction and distortion).

Example 3: correlated errors non-differential (undirected) measurement errors

Table 3 G ₃ illustrates the structure of correlated non-differential (undirected) measurement error bias, which arises when the error terms of the treatment and outcome share a common cause.

Consider an example: imagine that societies with more sophisticated record-keeping systems tend to offer more precise and comprehensive records of both beliefs in big Gods and of social complexity. In this setting, it is the record-keeping systems that give the illusion of a relationship between big Gods and social complexity. This might occur without any causal effect of big-God beliefs on measuring social complexity or vice versa. Nevertheless, the correlated sources of error for both the exposure and outcome might suggest causation in its absence.

Correlated non-differential measurement error invites weird results (wrongly estimated inferences owing to inappropriate restriction and distortion).

Example 4: uncorrelated differential measurement error: exposure affects error of outcome

Table 3 G ₄ illustrates the structure of uncorrelated differential (or directed) measurement error, where a non-causal path is opened linking the treatment, the outcome or a common cause of the treatment and outcome.

Continuing with our previous example, imagine that beliefs in big Gods lead to inflated records of social complexity in a culture's record-keeping. This might happen because the record keepers in societies that believe in big Gods prefer societies to reflect the grandeur of their big Gods. Suppose further that cultures lacking beliefs in big Gods prefer Bacchanalian-style feasting to record-keeping. In this scenario, societies with record keepers who believe in big Gods would appear to have more social complexity than equally complex societies without such record keepers.

Uncorrelated directed measurement error bias also invites weird results (wrongly estimated inferences owing to inappropriate restriction and distortion).

Example 5: uncorrelated differential measurement error: outcome affects error of exposure

Table 3 G ₅ illustrates the structure of uncorrelated differential (or directed) measurement error, this time when the outcome affects the recording of the treatment that preceded the outcome.

Suppose that ‘history is written by the victors’. Can we give a structural account of measurement error bias arising from such selective retention of the past? Suppose that social complexity causes beliefs in big Gods. Perhaps kings create big Gods after the image of kings. If the kings prefer a history in which big Gods were historically present, this might bias the historical record, opening a path of association that reverses the order of causation. Such results would be weird (wrongly estimated inferences owing to inappropriate restriction and distortion).

Example 6: uncorrelated differential error: outcome affects error of exposure

Table 3 G ₆ illustrates the structure of correlated differential (directed) measurement error, which occurs when the exposure affects levels of already correlated error terms.

Suppose social complexity produces a flattering class of religious elites who produce vainglorious depictions of kings and their dominions and also of the extent and scope of their society's beliefs in big Gods. For example, such elites might downplay widespread cultural practices of worshipping lesser gods, inflate population estimates and overstate the range of the king's political economy. In this scenario, the errors of the exposure and of the outcome are both correlated and differential.

Results based on such measures might be weird (wrongly estimated inferences owing to inappropriate restriction and distortion).

Summary

In Part 1, we examined four types of measurement error bias: independent, correlated, dependent and correlated dependent. The structural features of measurement error bias clarify how measurement errors threaten causal inferences. Considerably more could be said about this topic. For example, VanderWeele and Hernán (Reference VanderWeele and Hernán2012) demonstrate that, under specific conditions, we can infer the direction of a causal effect from observed associations. Specifically, if:

1. (1) the association between the measured variables $A_1^{\prime}$ and $Y_2^{\prime}$ is positive;

2. (2) the measurement errors for these variables are not correlated; and

3. (3) we assume distributional monotonicity for the effect of A on Y (applicable when both are binary);

then a positive observed association implies a positive causal effect from A to Y. Conversely, a negative observed association provides stronger evidence for a negative causal effect if the error terms are positively correlated than if they are independent. This conclusion relies on the assumption of distributional monotonicity for the effect of A on Y. For now, the four elementary structures of measurement error bias will enable us to clarify the connections between the structures of measurement error bias, target population restriction bias at the end of a study, and target restriction bias at the start of a study.

We will return to measurement error again in Part 4. Next, we focus on structural features of bias when there is an inappropriate restriction of the target population in the analytic sample at the end of study.

Example 1: confounding by common cause of treatment and attrition

Table 4 G ₁ illustrates confounding by common cause of treatment and outcome in the censored such that the potential outcomes of the population at baseline Y(a) may differ from those of the censored population at the end of study Y ^′(a) such that Y ^′(a) ≠ Y(a).

Table 4. Five examples of right-censoring bias

Key:

A denotes the treatment;

Y denotes the outcome;

U denotes an unmeasured confounder;

$ {\cal R} $ denotes randomisation into treatment;

asserts causality

biased path for treatment effect in the target population.

indicates a latent variable X measured by proxy X′.

indicates a path for bias linking A to Y absent causation.

indicates that conditioning on X introduces bias.

indicates effect modification of by X.

indicates effect modification of by $U_{\Delta ^F}$

Suppose investigators are interested in whether religious service attendance affects volunteering. Suppose that an unmeasured variable, loyalty, affects religious service attendance, attrition and volunteering. The structure of this bias reveals an open backdoor path from the treatment to the outcome.

We have encountered this bias before. The structure we observe here is one of correlated measurement errors (Table 3 G ₃). In this example, attrition may exacerbate measurement error bias by opening a path from

The results obtained from such a study would be distorted – that is, weird (wrongly estimated inferences owing to inappropriate restriction and distortion). Here, distortion operates through the restriction of the target population in the analytic sample population at the end of the study.

Example 2: treatment affects censoring

Table 4 G ₂ illustrates bias in which the treatment affects the censoring process. Here, the treatment causally affects the outcome reporter but does not affect the outcome itself.

Consider a study investigating the effects of mediation on well-being. Suppose there is no treatment effect but that Buddha-like detachment increases attrition. Suppose those with lower Buddha-like detachment report well-being differently than those with higher Buddha-like detachment. Buddha-like detachment is not a cause of well-being, we suppose; however, we also suppose that it is a cause of measurement error in the reporting of well-being. In this setting, we discover a biasing path that runs: (). Note that there is no confounding bias here because there is no common cause of the treatment and the outcome.

We have encountered this structural bias before. The structure we observe here is one of directed uncorrelated measurement error (Table 3 G ₄). Randomisation ensures no backdoor paths. However, if the intervention affects both attrition and how the outcome is reported the treatment will cause measurement error bias (note this is not confounding bias because the treatment and outcome do not share a common cause.)

The results obtained from such a study risk distortation, inviting weirdness (wrongly estimated inferences owing to inappropriate restriction and distortion). Here, distortion operates through the restriction of the target population at the end of the study, assuming the analytic sample at the start of the study represented that target population (or was weighted to represent it).

Example 3: no treatment effect when outcome causing censoring

Table 4 G ₃ illustrates the structure of bias when there is no treatment effect yet the outcome affects censoring.

If G ₃ faithfully represents reality, under the sharp null we would generally not expect bias in the average treatment effect estimate from attrition. The structure we observe here is again familiar: it is one of undirected uncorrelated measurement error (Table 3 G ₁). However, as before, at the start of study it is generally unclear whether the sharp null holds (if it were clear, there would be no motivation for the study). In theory, however, although the analytic sample population in the setting we have imagined would be a restriction of the target population, such a restriction of the target population is not expected to bias the null result. Again, we consider this example for its theoretical interest; no statistical test could validate what amounts to a structural assumption of the sharp null.

Example 4: treatment effect when outcome causes censoring and there is a true treatment effect

Table 4 G ₄ illustrates the structure of bias when the outcome affects censoring in the presence of a treatment effect. If the true outcome is an effect modifier of the measured outcome, we can expect bias in at least one measure of effect (e.g. the risk ratio or the causal difference scale). We return to this form of bias with a worked example in Part 4, where we clarify how such bias may arise even without confounding. We shall see that the bias described in Table 4 G ₄ is equivalent to measurement error bias. For now, we note that the results of the study we have imagined here would be weird (wrongly estimated inferences owing to inappropriate restriction and distortion).

Example 5: treatment effect and effect-modifiers differ in censored (restriction bias without confounding)

Table 4 G ₅ represents a setting in which there is a true treatment effect, but the distribution of effect-modifiers – variables that interact with the treatment – differs among the sample at baseline and the sample at the end of the study. Knowing nothing else, we might expect this setting to be standard. Where measured variables are sufficient to predict attrition, that is, where missingness is at random, we can obtain valid estimates for a treatment effect by inverse probability of treatment weighting (Cole & Hernán, Reference Cole and Hernán2008; Leyrat et al., Reference Leyrat, Carpenter, Bailly and Williamson2021) or by multiple imputation – on the assumption that our models are correctly specified (Shiba & Kawahara, Reference Shiba and Kawahara2021). However, if missingness is not completely at random, or if our models are otherwise misspecified, then causal estimation is compromised (Malinsky et al., Reference Malinsky, Shpitser and Tchetgen Tchetgen2022; Tchetgen Tchetgen & Wirth, Reference Tchetgen Tchetgen and Wirth2017).

Note that Table 4 G ₅ closely resembles a measurement structure we have considered before, in Part 1: Table 3 G ₂. Replacing the unmeasured effect modifiers and U _ΔF in Table 4 G ₅ for in Table 3 G ₂ reveals that the unmeasured effect modification in the present setting can be viewed as an example of uncorrelated independent measurement error when there is a treatment effect (i.e. censoring ‘off the null’.)

In the setting we describe in Table 4 G ₅ there is a common cause of the treatment and outcome. Nevertheless, the analytic sample population at the end-of-study is an undesirable restriction of the target population because the marginal effect estimate for this analytic sample population will differ from that of the target population (refer to supplementary materials S4 for a simulation that covers applies to this setting). We infer that results in this setting just described permit weirdness (wrongly estimated inferences owing to inappropriate restriction and distortion) because censoring leads to inappropriate restriction.

Summary

In this section, we examined how right-censoring, or attrition, can lead to biased causal effect estimates. Even without confounding bias, wherever the distribution of variables that modify treatment effects differs between the analytic sample population at the start and end of the study, the average treatment effects may differ, leading to biased estimates for the target population. To address such bias, investigators must ensure that the distribution of potential outcomes at the end of the study corresponds with that of the target population. Again, methods such as inverse probability weighting and multiple imputation can help mitigate this bias (refer to Bulbulia, Reference Bulbulia2024a).

The take-home message is this: attrition is nearly inevitable, and if attrition cannot be checked it will make results weird (wrongly estimated inferences owing to inappropriate restriction and distortion). Refer to supplementary materials S3 for a mathematical explanation of why effects differ when the distribution of effect modifiers differs. Refer to supplementary materials S4 for a data simulation that makes the same point.

Next, we investigate target population restriction bias at the start of the study (left-censoring). We shall discover that structural motifs of measurement error bias reappear.

Target population restriction bias at baseline can be collider-restriction bias

Table 5 G ₁ illustrates an example of target population restriction bias at baseline in which there is collider-restriction bias.

Table 5. Collider-Stratification bias at the start of a study (‘M-bias’)

Suppose investigators want to estimate the causal effects of regular physical activity, A, and heart health, Y, among adults visiting a network of community health centres for routine check-ups.

Suppose there are two unmeasured variables that affect selection into the study S = 1:

1. (1) Health awareness, U1, an unmeasured variable that influences both the probability of participating in the study, $\fbox{{S = 1}}$, and the probability of being physically active, A. Perhaps people with higher health awareness are more likely to (1) engage in physical activity and (2) participate in health-related studies.

2. (2) Socioeconomic status (SES), U2, an unmeasured variable that influences both the probability of participating in the study, $\fbox{{S = 1}}$, and heart health, Y. We assume that individuals with higher SES have better access to healthcare and are more likely to participate in health surveys; they also tend to have better heart health from healthy lifestyles: joining expensive gyms, juicing, long vacations and the like.

As presented in Table 5 G ₁, there is collider-restriction bias from conditioning on S = 1:

1. (1) U1 – because individuals with higher health awareness are more likely to be both physically active and participate in the study, the subsample over-represents physically active individuals. This overestimates the prevalence of physical activity, setting up a bias in overstating the potential benefits of physical activity on heart health in the general population.

2. (2) U2 – because individuals with higher SES may have better heart health from SES-related factors, this opens a confounding path from physical activity and heart health through the selected sample, setting up the investigators for the potentially erroneous inference that physical activity has a greater positive impact on heart health than it actually does in the general population. The actual effect of physical activity on heart health in the general population might be less pronounced than observed.

It might seem that researchers would need to sample from the target population. However, Table 5 $\cal{G}$ makes it clear that by adjusting for health awareness or SES or a proxy for either, researchers may block the open path arising from collider stratification bias. After such conditioning, we should expect a null effect in the sample population just as in the target population.

The next series of examples illustrates challenges to obtaining valid causal effect estimates in the presence of interactions.

Target population restriction bias at baseline without collider-restriction bias at baseline

Problem 1: the target population is not WEIRD (western, educated, industrialised, rich and democratic); the analytic sample population is WEIRD

Table 6 G _1.1 presents a scenario for target population restriction bias at baseline. When the analytic sample population obtained at baseline differs from the target population in the distributions of variables that modify treatment effects, effect estimates may be biased, even without confounding bias. Results may be weird without arising from confounding bias. This problem has been recently considered in Schimmelpfennig et al. (Reference Schimmelpfennig, Spicer, White, Gervais, Norenzayan, Heine and Muthukrishna2024).

Table 6. The association in the population of selected individuals differs from the causal association in the target population. Hernán (Reference Hernán2017) calls this scenario ‘selection bias off the null’. Lu et al. (Reference Lu, Cole, Howe and Westreich2022) call this scenario ‘Type 2 selection bias’. We call this bias ‘target population restriction bias at baseline’

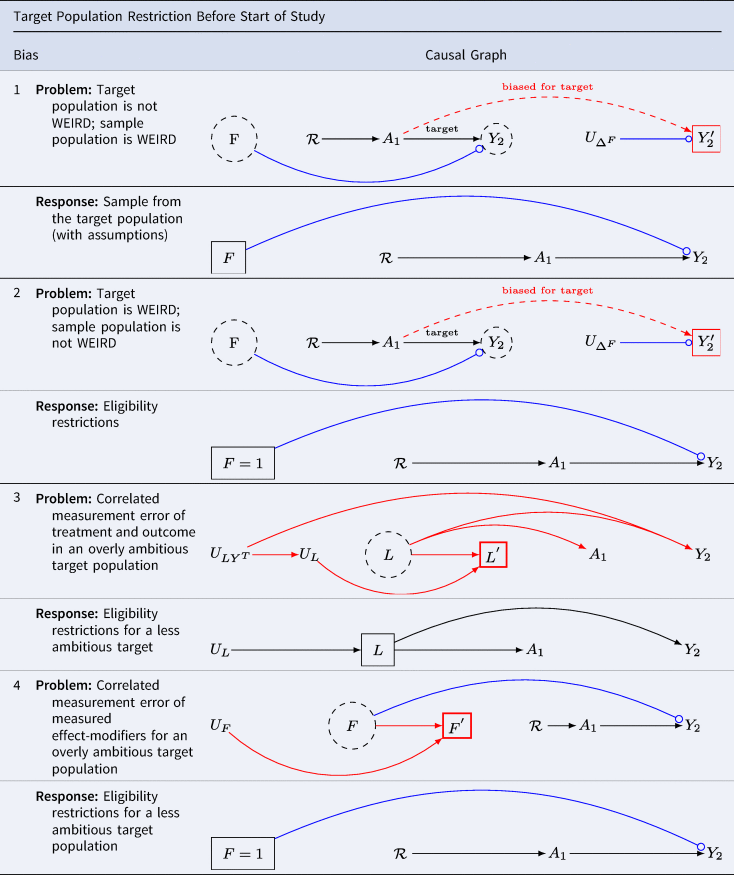
Key: A denotes the treatment; Y denotes the outcome; asserts causality; indicates conditioning on variable X; indicates fixing co-variate to level X = 1; indicates effect modification of by F; biased path for treatment effect arising from confounding by a common cause; biased path for treatment effect in target population; indicates a latent variable X measured by proxy X′; indicates that conditioning on X introduces bias.

Suppose we are interested in the effects of political campaigning but only sample from our preferred political party. Results for the general population will be distorted if the distribution of effect modifiers of the treatment varies by party. One such effect modifier might be ‘party affiliation’. This valid concern underscores the call for broader sampling in the human sciences. WEIRD samples will not be informative for science generally whenever the distribution of effect modifiers among humans differs from those of the restricted population of humans from which WEIRD analytic samples are drawn.

Note that we have encountered Table 6 G _1.1 twice before. It is the same causal directed acyclic graph as we found in Table 5 G ₅. As we did before, we may replace the unmeasured effect modifiers and U _ΔF for in Table 3 G ₂ and observe that we recover uncorrelated measurement error ‘off the null’ (i.e. when there is a true treatment effect).

The structural similarity suggests options might be easily overlooked. Where the distributions of treatment-effect modifiers are known and measured and where census (or other) weights are available for the distributions of effect modifiers in the target population, it may be possible to weight the sample to more closely approximate the target population parameters of interest (Stuart et al., Reference Stuart, Bradshaw and Leaf2015).

Let $\widehat{{ATE}}_{\rm target}$ denote the population average treatment effect for the target population. Let $\widehat{{ATE}}_{{\rm restricted}}$ denote the average treatment effect at the end of treatment. Let W denote a set of variables upon which the restricted and target populations structurally differ. We say that results generalise if we can ensure that:

$$\widehat{{ATE}}_{\rm target} = \widehat{{ATE}}_{\rm restricted}$$

or if there is a known function such that

$$ATE_{\rm target}\approx f_W( ATE_{{\rm restricted}}, \;W) $$

In most cases, f _W will be unknown, as it must account for potential heterogeneity of effects and unobserved sources of bias. For further discussion on this topic, see Imai et al. (Reference Imai, King and Stuart2008), Cole and Stuart (Reference Cole and Stuart2010) and Stuart et al. (Reference Stuart, Ackerman and Westreich2018).

Table 6 G _1.2 provides a graphical representation of the solution.

Importantly, if there is considerable heterogeneity across humans, then we might not know how to interpret the average treatment effect for the target population of all humans even if this causal effect can be estimated. In comparative research, we are often precisely interested in treatment heterogeneity. If we seek explicitly comparative models, however, we will need to ensure the validity of estimates for every sample that we compare. If one stratum in the comparative study is weird (wrongly estimated inferences owing to inappropriate restriction and distortion), errors will propagate to the remainder of the comparative study. To understand such propogation consider scenarios where the target population is a deliberate restriction of the the source population from which the analytic sample at baseline is drawn. We deliberately seek restriction wherever ‘eligibility criteria’ are desirable for a study. Although this point is perhaps obvious, Although this point is perhaps obvious, many observational studies do not report eligibility criteria.

Measurement error in the treatment biases causal contrasts because the treatment reporter is a post-treatment collider

Table 7 G _1.1 presents a single world intervention template from which we may generate two counterfactual states of the world under two distinct interventions $A = \tilde{a}\in \{ 0, \;1\}$. We call the measurement of the intervention a ‘reporter of A’ and denote the state of the reporter under $A = \tilde{a}$ as $B( \tilde{a})$. In our convention, if a node in a SWIG (or template) is unobserved, we shade it in grey. E ^A denotes an unmeasured variable or set of variables that cause the reporter $B( \tilde{a})$ to differ from $\tilde{a}$, the fixed state of the intervention when A is set to $\tilde{a}$. In template Table 7 G _1.1, $A = \tilde{a}$ remains unobserved. The only observed nodes are $B( \tilde{a})$ and $Y( B( \tilde{a}) )$, which is the potential outcome for Y as reported by $B( \tilde{a})$. Note that here we include reporters of the unobserved true state of the treatment directly in our representation of the causal order as encoded in our SWIG. Table 7 G _1.2 corresponds to the assumed state of the world when the reporter of A is set to B(0). Table 7 G _1.3 corresponds to the assumed state of the world when the reporter of A is set to B(1); in this world, investigators observe Y(B(1)). We assume that E ^A is independent of both A and $Y( \tilde{a})$. However, we assume that E ^A causes $B( \tilde{a})$ to differ from the true state $A = \tilde{a}$. As a result of this misclassification, we have no assurance whether ${\rm \mathbb{E}}[Y(B(1))-Y(B(0))] = {\rm \mathbb{E}}[Y(1)-Y(0)]$. The SWIGs make it apparent that although A is independent of E ^A, $A = \tilde{a}$ and E ^A become statistically entangled in the reporter $B( \tilde{a})$, and it is this reporter, not the unobserved true state of $Y( \tilde{a})$, that investigators record.

Table 7. Uncorrelated/Undirected Measurement Error in Single-World Intervention Graph. There is no ‘action at a distance’: all measurement errors have causes; errors entering reporters of the treatment and outcome clarify that the treatment reporter induces collider bias, and the outcome reporter induces effect modification during estimation

Key: $Y( \tilde{{\bf a}}) $ denotes the the true outcome; $A = \tilde{a}$ a denotes the true treatment. $B( \tilde{{\bf a}}) $ denotes the mismeasured treatment; $V( B( \tilde{{\bf a}}) ) $ denotes the mismeasured outcome; E^A: unmeasured variable(s) that, together with $A = \tilde{{\bf a}}$ cause measurement: $B( \tilde{{\bf a}}) $; E^Y Unmeasured variable(s) that, together with $Y( \tilde{{\bf a}}) $ cause measurement: $V( \tilde{{\bf a}}) $; Shaded nodes are unobserved. Treatment reporter bias: $\mathbb{E}[ Y( B( \tilde{{\bf a}}) ) ] \ne \mathbb{E}[ Y( \tilde{{\bf a}}) ] $; Outcome reporter bias: $\mathbb{E}[ V( Y( \tilde{{\bf a}}) ) ] \ne \mathbb{E}[ Y( \tilde{{\bf a}}) ] $.

Consider the following example. Coach Alice randomly assigns one of two running programmes to club runners: A = 1 (train), A = 0 (do not train). Alice is not interested in estimating the effect of random treatment assignment (the intent-to-treat effect). Rather, she wants to understand the causal effect of training compared with rest – a per-protocol effect. Unknown to Alice, 20% do not follow the programme. Table Table 7 G _1.1 is a SWIG template that presents bias from measurement error in the treatment. The template serves as a ‘graph value function’ that generates SWIGs: Table 7 G _1.1, in which all runners receive A = 0 (do not train), and Table 7 G _1.2, in which all runners receive A = 1 (train). Here, B(0) and B(1) denote the reporters of the level of the intervention.

Again, we note that the treatment recorded is not the per-protocol effect ${\rm \mathbb{E}}[Y(1)-Y(0)]$ but rather the intention-to-treat effect ${\rm \mathbb{E}}[Y(B(1))-Y(B(0))]$. Generally, the effect we obtain will understate the per-protocol effect of training both on the difference scale and the risk ratio scale. Those who were assigned to training but rest will dilute the effect of training: ${\rm \mathbb{E}}[Y(1)]> {\rm \mathbb{E}}[Y(B(1))]$. Those who were assigned to rest but who nevertheless train will inflate the expected effect of resting: ${\rm \mathbb{E}}[Y(B(1))] > {\rm \mathbb{E}}[Y(1)]$. Hence:

$${\rm \mathbb{E}}[ Y( 1) -Y( 0) ] > {\rm \mathbb{E}}[ Y( B( 1) ) -Y( B( 0) ) ] $$

Note that attenuation of a true treatment effect in a setting of uncorrelated errors is not guaranteed (Jurek et al., Reference Jurek, Greenland and Maldonado2008; Lash et al., Reference Lash, Rothman, VanderWeele and Haneuse2020). The SWIGs in Table 7 G _1.1–1.3 make the general measurement bias problem clear: although the treatment that is estimated remains d-separated from the potential outcomes, the causal contrast that we obtain at the end of the study is not the treatment we seek and will often (although not always) diminish a true treatment effect because the reporter under treatment is a common effect of the unmeasured source of bias and the treatment that has been applied, and it is the outcomes under mismeasured treatments that investigators contrast.

Measurement error in the outcome biases causal contrasts because the unmeasured error of the outcome is an effect modifier of the outcome reporter

Table 7 G _2.1 presents a single world intervention template from which we may generate two counterfactual states of the world under two distinct interventions $A = \tilde{a}\in \{ 0, \;1\}$. Here, the treatment is observed and recorded without error. Hence we do not include a reporter of the treatment. However, the true outcome is not observed, but only reported with error. E ^Y denotes the unmeasured source of error in the reporting of $Y( \tilde{a})$, which we assume to be independent of A and of Y. We shade these nodes in grey because both E ^Y and $Y( \tilde{a})$ are not observed. The node $V( Y( \tilde{a}) )$ denotes the observed state of Y when $A = \tilde{a}$. In template Table 7 G _2.1, $A = \tilde{a}$ remains unobserved. Table 7 G _2.2 corresponds to the assumed state of the world when A = 0 and Y(0) is reported with error as V(Y(0)). Likewise, Table 7 G _2.3 corresponds to the assumed state of the world when A = 1 and Y(1) is reported with error as V(Y(1)). We assume that E ^Y is independent of A and of Y. Misclassification will tend to increase the variance of the estimated treatment effect. If the outcome is continuous, the expected difference in the mean of the outcome for the reported outcome may differ from that for the true outcome. How bias affects the outcome will vary depending on the scale we use to evaluate such bias.

Suppose that under training, the athlete runs a marathon in 3 hours, and under rest, they run a marathon in 4 hours. To keep figures easy, we will use round numbers. Suppose the bias in reporting is 1 hour. Thus, we have ${\rm \mathbb{E}}[Y(1)] = 3$, ${\rm \mathbb{E}}[Y(0)] = 4$; ${\rm \mathbb{E}}[V(Y(1))] = 2$ and ${\rm \mathbb{E}}[V(Y(0))] = 3$.

$${\rm ATE\;Difference\;Scale\colon \;no\;measurement\;error} = {\rm \mathbb{E}}[ Y( 1) ] -{\rm \mathbb{E}}[ Y( 0) ] = 3-4 = {-}1$$

$${\rm ATE\;Difference\;Scale\colon \;measurement\;error} = {\rm \mathbb{E}}[ V( Y( 1) ) ] -{\rm \mathbb{E}}[ V( Y( 0) ) ] = 2-3 = {-}1$$

The effect estimates do not differ:

$${\rm ATE\;no\;measurement\;error} = {\rm ATE\;measurement\;error}$$

However, consider this bias on the risk ratio scale:

$${\rm ATE\;Risk\;Ratio\;Scale\colon \;no\;measurement\;error} = {\rm \mathbb{E}}[ Y( 1) ] {\rm /\mathbb{E}}[ Y( 0) ] = 3{\rm /}4 = 0.75$$

$${\rm ATE\;Risk\;Ratio\;Scale\colon \;measurement\;error} = {\rm \mathbb{E}}[ V( Y( 1) ) ] {\rm /\mathbb{E}}[ V( Y( 0) ) ] = 2{\rm /}3 = 0.66$$

These effect estimates differ:

$${\rm ATE\;RR\;no\;measurement\;error}\ne {\rm ATE\;RR\;measurement\;error}$$

Imagine that the bias was positive, such that runners added an hour to their times – perhaps the runners do not want to stand out. The true risk ratio for the treatment remains 0.75. However, the biased risk ratio for the treatment would become:

$${\rm ATE\;Risk\;Ratio\;Scale\colon \;measurement\;error} = {\rm \mathbb{E}}[ V( Y( 1) ) ] {\rm /\mathbb{E}}[ V( Y( 0) ) ] = 4{\rm /}5 = 0.8$$

Here we would understate the true treatment effect. The SWIGs (Table 7 G _2.1–2.3) make clear the reason for the scale sensitivity of the bias. Although the source of bias in the outcome (E ^Y) is independent of the treatment (A), E ^Y functions as an effect modifier for the reported outcome $V( Y( \tilde{a}) )$.

Consider: it has long been understood that where treatment effects vary across different population strata, an estimate of the causal effect on the risk difference scale will differ from the estimate on the risk ratio scale (Greenland, Reference Greenland2003). Here, we find that reporters of the outcome are subject to similar relativity. For example, we might have constructed a multiplicative error function for the outcome such that we subtract 1 hour if the response is 3 and subtract 1.344 if the response is 4. Under this error function, the risk ratio would remain stable at 0.75 irrespective of whether the outcome was measured with error; however, the risk difference would no longer be constant.

Note that we have encountered SWIGs Table 7 G _1.2–1.3 and Table 7 G _2.2–2.3 before. These causal graphs are structurally equivalent to the causal directed acyclic graph in Part 1 Table 3 G ₂, in which we considered uncorrelated independent measurement error. Moreover, Table 7 G _2.2–2.3 is equivalent to Part 2 Table 4 G ₅, in which we considered target-restriction bias without confounding; and Part 3 Table 5 G ₁, G ₂, G ₄ in which we considered target population restriction biases in the analytic sample at the start of the study. Single world intervention graphs are useful in providing a more detailed representation of causality in which the biases that give rise to biased causal effect estimates when there is measurement error bias ‘off the null’ – such as when restricted representation of the target population by the analytic sample at the start or end invalidates the causal inferences we seek for the target population.

Measurement error in the treatment or outcome will not modify a strictly ‘null’ effect

As shown in Table 7 G _1.4 and Table 7 G _2.4, if we assume randomisation into treatments, or equivalently if we assume no unmeasured confounding conditional on perfectly measured covariates, we will not expect a biasing path leading to an association between treatment and outcome. However, a strict ‘null’ effect cannot be assumed. Note that we do not use ‘null’ here in the sense of null hypothesis significance testing, where there is no such thing as a ‘null’ effect. Supplementary materials S5 uses SWIGs to describe correlated and directed measurement error and consider how bias correction may be interpreted mechanistically as interventions on reporters.

Summary of part 4

We have characterised target-population restriction bias, whether at the start or the end of the study, as formally equivalent to undirected uncorrelated measurement error. Here, SWIGs allow us to apply lessons from the study of effect modification to the analysis of measurement error biases. As shown in G _2.1–2.3, SWIGs greatly clarify how measurement error bias for the outcome arises in the absence of confounding bias: the unmeasured causes of error function as effect modifiers of the outcome reporters, such that causal contrasts will differ on at least one scale of effect ‘off the null’. The mathematical explanation in supplementary materials S3 for threats to external validity from right censoring applies equally to threats from left censoring, as does the simulation in supplementary materials S4.

Note that all of the biases we have considered cannot be evaluated by statistical tests. For example, even if investigators were to obtain satisfactory test statistics for metric, configural and scalar equivalence, they would be unable to diagnose target population restriction biases with these tests. Nor would we be able to diagnose other forms of measurement error biases using statistical tests. Rather, they can only evaluate evidence for bias by first representing the causal structures they assume hold in the world, and investigating the implications of each assumption one by one. Likewise, we cannot take the invalidation of standard statistical tests as evidence that similar causal effects underpin sample responses to the interventions of interest. Assumptions alone do not clarify the causal realities that give rise to them. A similar point about the role of assumptions in comparative research is made in Schimmelpfennig et al. (Reference Schimmelpfennig, Spicer, White, Gervais, Norenzayan, Heine and Muthukrishna2024).