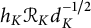1 Introduction
Let K be a number field of degree
![]() $n \geqslant 3$
, signature
$n \geqslant 3$
, signature
![]() $(r_1,r_2)$
, discriminant
$(r_1,r_2)$
, discriminant
![]() $(-1)^{r_2}d_K$
, class number
$(-1)^{r_2}d_K$
, class number
![]() $h_K$
, regulator
$h_K$
, regulator
![]() $\mathcal {R}_K$
, and let
$\mathcal {R}_K$
, and let
![]() $w_K$
be the number of roots of unity in K. Let
$w_K$
be the number of roots of unity in K. Let
![]() $\kappa _K$
be the residue at
$\kappa _K$
be the residue at
![]() $s=1$
of the Dedekind zeta-function
$s=1$
of the Dedekind zeta-function
![]() $\zeta _K(s)$
attached to K. Estimating
$\zeta _K(s)$
attached to K. Estimating
![]() $h_K$
is a long-standing problem in algebraic number theory. One of the classic way is the use of the so-called analytic class number formula stating that
$h_K$
is a long-standing problem in algebraic number theory. One of the classic way is the use of the so-called analytic class number formula stating that
and to use Hecke’s integral representation and the functional equation of the Dedekind zeta-function to majorize
![]() $\kappa _K$
. This is done in [Reference Louboutin7, Reference Louboutin8] with additional properties of log-convexity of some functions related to
$\kappa _K$
. This is done in [Reference Louboutin7, Reference Louboutin8] with additional properties of log-convexity of some functions related to
![]() $\zeta _K$
which enables Louboutin to reach the following bound:
$\zeta _K$
which enables Louboutin to reach the following bound:
 $$ \begin{align} h_K \mathcal{R}_K \leqslant \frac{w_K}{2} \left( \frac{2}{\pi} \right)^{r_2} \left( \frac{e \log d_K}{4n-4} \right)^{n-1} d_K^{1/2}. \end{align} $$
$$ \begin{align} h_K \mathcal{R}_K \leqslant \frac{w_K}{2} \left( \frac{2}{\pi} \right)^{r_2} \left( \frac{e \log d_K}{4n-4} \right)^{n-1} d_K^{1/2}. \end{align} $$
Let
![]() $r_K(m)$
be the mth coefficient of
$r_K(m)$
be the mth coefficient of
![]() $\zeta _K$
, i.e., the number of nonzero integral ideals of
$\zeta _K$
, i.e., the number of nonzero integral ideals of
![]() $\mathcal {O}_K$
of norm m, and denote
$\mathcal {O}_K$
of norm m, and denote
![]() $\Delta _K(x)$
to be the error term in the Ideal Theorem, i.e.,
$\Delta _K(x)$
to be the error term in the Ideal Theorem, i.e.,
The aim of this work is to prove the following result.
Theorem 1.1 Let K be an algebraic number field of degree
![]() $n \geqslant 3$
, and set
$n \geqslant 3$
, and set
![]() $\gamma _3 = 214$
and
$\gamma _3 = 214$
and
![]() $\gamma _n = 10$
if
$\gamma _n = 10$
if
![]() $n \geqslant 4$
. Assume that there exist
$n \geqslant 4$
. Assume that there exist
![]() $\alpha \in \left ( 0,\frac {2}{n} \right )$
and a constant
$\alpha \in \left ( 0,\frac {2}{n} \right )$
and a constant
such that, for
![]() $x \geqslant 1,$
$x \geqslant 1,$
where
![]() $\Delta _K(x)$
is given in (1.3). Then
$\Delta _K(x)$
is given in (1.3). Then
 $$ \begin{align*} h_K \mathcal{R}_K < \frac{3w_K}{2} \left( \frac{2}{\pi} \right)^{r_2} \left( \frac{\left( \frac{1}{2 \alpha} \log C_K \right)^{n-1}}{(n-1)!} - \frac{\left( \frac{1}{2 \alpha} \log C_K \right)^{n-2}}{(n-2)!} \right) d_K^{1/2}. \end{align*} $$
$$ \begin{align*} h_K \mathcal{R}_K < \frac{3w_K}{2} \left( \frac{2}{\pi} \right)^{r_2} \left( \frac{\left( \frac{1}{2 \alpha} \log C_K \right)^{n-1}}{(n-1)!} - \frac{\left( \frac{1}{2 \alpha} \log C_K \right)^{n-2}}{(n-2)!} \right) d_K^{1/2}. \end{align*} $$
2 Tools
The first lemma is a Titchmarsh-like generalization of [Reference Titchmarsh and Heath-Brown12, Theorem 12.5] to number fields established by Ayoub [Reference Ayoub1]. The result is stated for the quadratic case, but as it can be seen in the proof and as the author points it out, it is still true for the general case (see also [Reference Ivić5, Lemma 13.3]).
Lemma 2.1 Let
![]() $n \geqslant 3$
and
$n \geqslant 3$
and
![]() $\mu _K$
be the infimum of the real numbers
$\mu _K$
be the infimum of the real numbers
![]() $\sigma $
for which the integral
$\sigma $
for which the integral
 $$ \begin{align*} \int_{- \infty}^{\infty} \frac{| \zeta_K ( \sigma + it) |^2}{| \sigma + it |^2} \, \mathrm{d}t \end{align*} $$
$$ \begin{align*} \int_{- \infty}^{\infty} \frac{| \zeta_K ( \sigma + it) |^2}{| \sigma + it |^2} \, \mathrm{d}t \end{align*} $$
converges. Then
![]() $\mu _K \leqslant 1 - \frac {2}{n}$
and, for all
$\mu _K \leqslant 1 - \frac {2}{n}$
and, for all
![]() $\mu _K < \sigma < 1$
, we have
$\mu _K < \sigma < 1$
, we have
 $$ \begin{align*} \frac{1}{2 \pi} \int_{- \infty}^{\infty} \frac{| \zeta_K ( \sigma + it) |^2}{| \sigma + it |^2} \, \mathrm{d}t = \int_0^{\infty} \Delta_K(x)^2 x^{-1-2\sigma} \, \mathrm{d}x. \end{align*} $$
$$ \begin{align*} \frac{1}{2 \pi} \int_{- \infty}^{\infty} \frac{| \zeta_K ( \sigma + it) |^2}{| \sigma + it |^2} \, \mathrm{d}t = \int_0^{\infty} \Delta_K(x)^2 x^{-1-2\sigma} \, \mathrm{d}x. \end{align*} $$
Proof Assume
![]() $\frac {1}{n} \leqslant \sigma \leqslant 1 - \frac {1}{n}$
. By [Reference Chandrasekharan and Narasimhan3, Theorem 4], we have, for all
$\frac {1}{n} \leqslant \sigma \leqslant 1 - \frac {1}{n}$
. By [Reference Chandrasekharan and Narasimhan3, Theorem 4], we have, for all
![]() $\varepsilon> 0,$
$\varepsilon> 0,$
The exponent of T is less than
![]() $2$
for
$2$
for
![]() $\sigma> 1 - \frac {2-\varepsilon }{n}$
and note that
$\sigma> 1 - \frac {2-\varepsilon }{n}$
and note that
![]() $1 - \frac {2}{n} \geqslant \frac {1}{n}$
since
$1 - \frac {2}{n} \geqslant \frac {1}{n}$
since
![]() $n \geqslant 3$
. This implies that
$n \geqslant 3$
. This implies that
 $$ \begin{align*} \int_{T/2}^T \frac{| \zeta_K ( \sigma + it) |^2}{| \sigma + it |^2} \, \mathrm{d}t \ll T^{- \eta} \end{align*} $$
$$ \begin{align*} \int_{T/2}^T \frac{| \zeta_K ( \sigma + it) |^2}{| \sigma + it |^2} \, \mathrm{d}t \ll T^{- \eta} \end{align*} $$
for some
![]() $\eta = \eta (\varepsilon )>0$
. Now replacing T by
$\eta = \eta (\varepsilon )>0$
. Now replacing T by
![]() $2^{-j}T$
and summing over
$2^{-j}T$
and summing over
![]() $j \geqslant 1$
yields
$j \geqslant 1$
yields
![]() $\mu _K \leqslant 1 - \frac {2}{n}$
. For the second part of the lemma, we start by using Perron’s formula [Reference Tenenbaum11, (2.3) p. 217] yielding
$\mu _K \leqslant 1 - \frac {2}{n}$
. For the second part of the lemma, we start by using Perron’s formula [Reference Tenenbaum11, (2.3) p. 217] yielding
where
![]() ${\sideset {^{\phantom {\prime }}}{^\prime }\sum }$
means that if x is a positive integer, then
${\sideset {^{\phantom {\prime }}}{^\prime }\sum }$
means that if x is a positive integer, then
![]() $\frac {1}{2} r_K(x)$
comes instead of
$\frac {1}{2} r_K(x)$
comes instead of
![]() $r_K(x)$
. Moving the line of integration to some
$r_K(x)$
. Moving the line of integration to some
![]() $1- (600)^{-2/3} n^{-7/3} \leqslant c < 1$
sufficiently close to
$1- (600)^{-2/3} n^{-7/3} \leqslant c < 1$
sufficiently close to
![]() $1$
, we get
$1$
, we get
so that
Using [Reference Stas9] (see also [Reference Bordellès2, Theorem 7.18]), there exists an absolute constant
![]() $c_0> 0$
such that, for
$c_0> 0$
such that, for
![]() $1- (600)^{-2/3} n^{-7/3} \leqslant c < \sigma < 1$
and
$1- (600)^{-2/3} n^{-7/3} \leqslant c < \sigma < 1$
and
![]() $t \geqslant e,$
$t \geqslant e,$
 $$ \begin{align*} \left| \frac{\zeta_K(\sigma+it)}{\sigma+it} \right| \leqslant e^{c_0 n^8 d_K^2} \, t^{600 n^{7/2} (1-\sigma)^{3/2}-1} (\log t)^{2/3} \leqslant e^{c_0 n^8 d_K^2} \, t^{-1} (\log t)^{2/3}, \end{align*} $$
$$ \begin{align*} \left| \frac{\zeta_K(\sigma+it)}{\sigma+it} \right| \leqslant e^{c_0 n^8 d_K^2} \, t^{600 n^{7/2} (1-\sigma)^{3/2}-1} (\log t)^{2/3} \leqslant e^{c_0 n^8 d_K^2} \, t^{-1} (\log t)^{2/3}, \end{align*} $$
so that
![]() $\zeta _K(s) s^{-1} \to 0$
uniformly in the strip
$\zeta _K(s) s^{-1} \to 0$
uniformly in the strip
![]() $1- (600)^{-2/3} n^{-7/3} \leqslant c < \sigma < 1$
as
$1- (600)^{-2/3} n^{-7/3} \leqslant c < \sigma < 1$
as
![]() $|t| \to \infty $
. Hence, on integrating over the rectangle
$|t| \to \infty $
. Hence, on integrating over the rectangle
![]() $d \pm i T$
,
$d \pm i T$
,
![]() $c \pm iT$
, with
$c \pm iT$
, with
![]() $\gamma _K < d < c < 1$
, we infer that (2.1) holds for any
$\gamma _K < d < c < 1$
, we infer that (2.1) holds for any
![]() $\gamma _K < c < 1$
. Replacing in (2.1) x by
$\gamma _K < c < 1$
. Replacing in (2.1) x by
![]() $1/x$
, taking
$1/x$
, taking
![]() $\gamma _K < c < 1$
, and using Parseval’s formula [Reference Ivić5, Identity (A5)] yields
$\gamma _K < c < 1$
, and using Parseval’s formula [Reference Ivić5, Identity (A5)] yields
 $$ \begin{align*} \frac{1}{2\pi} \int_{- \infty}^{\infty} \frac{| \zeta_K ( c + it) |^2}{| c + it |^2} \, \mathrm{d}t &= \int_0^{\infty} \Delta_K(1/x)^2 x^{2c-1} \, \mathrm{d}x \\ &= \int_0^{\infty} \Delta_K(u)^2 u^{-2c-1} \, \mathrm{d}u \end{align*} $$
$$ \begin{align*} \frac{1}{2\pi} \int_{- \infty}^{\infty} \frac{| \zeta_K ( c + it) |^2}{| c + it |^2} \, \mathrm{d}t &= \int_0^{\infty} \Delta_K(1/x)^2 x^{2c-1} \, \mathrm{d}x \\ &= \int_0^{\infty} \Delta_K(u)^2 u^{-2c-1} \, \mathrm{d}u \end{align*} $$
as required.
Corollary 2.2 Assume hypothesis (1.4), and let
![]() $0 < \delta < \alpha < \frac {2}{n}$
. Then
$0 < \delta < \alpha < \frac {2}{n}$
. Then
 $$ \begin{align*} \frac{1}{2 \pi} \int_{- \infty}^{\infty} \frac{| \zeta_K ( 1 - \delta + it) |}{| 1-\delta + it |^2} \, \mathrm{d}t \leqslant \frac{1}{2\sqrt{1-\delta}} \left( \frac{\kappa_K}{\sqrt{\delta}} + \frac{C_K}{\sqrt{\alpha-\delta}} \right). \end{align*} $$
$$ \begin{align*} \frac{1}{2 \pi} \int_{- \infty}^{\infty} \frac{| \zeta_K ( 1 - \delta + it) |}{| 1-\delta + it |^2} \, \mathrm{d}t \leqslant \frac{1}{2\sqrt{1-\delta}} \left( \frac{\kappa_K}{\sqrt{\delta}} + \frac{C_K}{\sqrt{\alpha-\delta}} \right). \end{align*} $$
Proof Using Lemma 2.1, (1.4) and the trivial bound
![]() $\left | \Delta _K(x) \right | \leqslant \kappa _K x$
when
$\left | \Delta _K(x) \right | \leqslant \kappa _K x$
when
![]() $x \in \left [ 0,1 \right )$
$x \in \left [ 0,1 \right )$
 $$ \begin{align*} \frac{1}{2 \pi} \int_{- \infty}^{\infty} \frac{| \zeta_K ( 1 - \delta + it) |^2}{| 1-\delta + it |^2} \, \textrm{d}t & \leqslant \kappa_K^2 \int_0^1 x^{2 \delta - 1} \textrm{d}x + C_K^2 \int_1^{\infty} x^{2 (\delta-\alpha) - 1 } \textrm{d}x \\ & = \frac{1}{2} \left( \frac{\kappa_K^2}{\delta} + \frac{C_K^2}{\alpha-\delta} \right), \end{align*} $$
$$ \begin{align*} \frac{1}{2 \pi} \int_{- \infty}^{\infty} \frac{| \zeta_K ( 1 - \delta + it) |^2}{| 1-\delta + it |^2} \, \textrm{d}t & \leqslant \kappa_K^2 \int_0^1 x^{2 \delta - 1} \textrm{d}x + C_K^2 \int_1^{\infty} x^{2 (\delta-\alpha) - 1 } \textrm{d}x \\ & = \frac{1}{2} \left( \frac{\kappa_K^2}{\delta} + \frac{C_K^2}{\alpha-\delta} \right), \end{align*} $$
and using the Cauchy–Schwarz inequality, we get
 $$ \begin{align*} & \frac{1}{2 \pi} \int_{- \infty}^{\infty} \frac{| \zeta_K ( 1 - \delta + it) |}{| 1-\delta + it |^2} \, \mathrm{d}t \\ & \quad \leqslant \frac{1}{2 \pi} \left( \int_{- \infty}^{\infty} \frac{| \zeta_K ( 1 - \delta + it) |^2}{| 1-\delta + it |^2} \, \textrm{d}t \right)^{1/2} \left( \int_{- \infty}^{\infty} \frac{\textrm{d}t}{ |1-\delta + it |^2} \right)^{1/2} \\ & \quad \leqslant \frac{1}{2 \sqrt{1 - \delta}} \left( \frac{\kappa_K^2}{\delta} + \frac{C_K^2}{\alpha - \delta} \right)^{1/2} \leqslant \frac{1}{2\sqrt{1-\delta}} \left( \frac{\kappa_K}{\sqrt{\delta}} + \frac{C_K}{\sqrt{\alpha-\delta}} \right) \end{align*} $$
$$ \begin{align*} & \frac{1}{2 \pi} \int_{- \infty}^{\infty} \frac{| \zeta_K ( 1 - \delta + it) |}{| 1-\delta + it |^2} \, \mathrm{d}t \\ & \quad \leqslant \frac{1}{2 \pi} \left( \int_{- \infty}^{\infty} \frac{| \zeta_K ( 1 - \delta + it) |^2}{| 1-\delta + it |^2} \, \textrm{d}t \right)^{1/2} \left( \int_{- \infty}^{\infty} \frac{\textrm{d}t}{ |1-\delta + it |^2} \right)^{1/2} \\ & \quad \leqslant \frac{1}{2 \sqrt{1 - \delta}} \left( \frac{\kappa_K^2}{\delta} + \frac{C_K^2}{\alpha - \delta} \right)^{1/2} \leqslant \frac{1}{2\sqrt{1-\delta}} \left( \frac{\kappa_K}{\sqrt{\delta}} + \frac{C_K}{\sqrt{\alpha-\delta}} \right) \end{align*} $$
as asserted.
Lemma 2.3 Uniformly for all
![]() $x \geqslant 1$
and all
$x \geqslant 1$
and all
![]() $n \in {\mathbb {Z}}_{\geqslant 1}$
, we have
$n \in {\mathbb {Z}}_{\geqslant 1}$
, we have
 $$ \begin{align*} \sum_{m \leqslant x} r_K (m) \log \frac{x}{m} \leqslant \frac{x \log x}{(n-1)!} \left( \log x+ n -1\right)^{n-2}. \end{align*} $$
$$ \begin{align*} \sum_{m \leqslant x} r_K (m) \log \frac{x}{m} \leqslant \frac{x \log x}{(n-1)!} \left( \log x+ n -1\right)^{n-2}. \end{align*} $$
Proof Let
![]() $\tau _n$
be the nth Piltz–Dirichlet divisor function. We have
$\tau _n$
be the nth Piltz–Dirichlet divisor function. We have
![]() $r_K (m) \leqslant \tau _n(m)$
and from the bound [Reference Bordellès2, Exercise 78]
$r_K (m) \leqslant \tau _n(m)$
and from the bound [Reference Bordellès2, Exercise 78]
 $$ \begin{align*} \sum_{m \leqslant t} \tau_n(m) \leqslant t \sum_{j=0}^{n-1} \binom{n-1}{j} \frac{(\log t)^j}{j!} \quad \left( t \geqslant 1 \right), \end{align*} $$
$$ \begin{align*} \sum_{m \leqslant t} \tau_n(m) \leqslant t \sum_{j=0}^{n-1} \binom{n-1}{j} \frac{(\log t)^j}{j!} \quad \left( t \geqslant 1 \right), \end{align*} $$
so that
 $$ \begin{align*} \sum_{m \leqslant x} r_K (m) \log \frac{x}{m} & = \int_1^x \frac{1}{t} \left( \sum_{m \leqslant t} r_K(m) \right) \, \textrm{d}t \\ & \leqslant \sum_{j=0}^{n-1} \binom{n-1}{j} \frac{1}{j!} \int_1^x (\log t)^j \, \textrm{d}t \\ &= x \sum_{j=0}^{n-1} \binom{n-1}{j} (-1)^j \left\lbrace \sum_{k=0}^j \frac{(- \log x)^k}{k!} - \frac{1}{x} \right\rbrace \\ &= - x \sum_{j=0}^{n-1} \binom{n-1}{j} (-1)^j \sum_{k=j+1}^{\infty} \frac{(- \log x)^k}{k!} \\ &= - x \sum_{k=1}^{\infty} \frac{(- \log x)^k}{k!} \ \sum_{j=0}^{\min(n-1,k-1)} (-1)^j \binom{n-1}{j} \\ &= -x \sum_{k=1}^{\infty} (-1)^{k+\min(n-1,k-1)}\frac{(\log x)^k}{k!} \binom{n-2}{\min(n-1,k-1)} \\ &= x \sum_{k=1}^{n-1} \frac{(\log x)^k}{k!} \binom{n-2}{k-1} \\ & \leqslant \frac{x \log x}{(n-1)!} \left( \log x+ n -1\right)^{n-2}, \end{align*} $$
$$ \begin{align*} \sum_{m \leqslant x} r_K (m) \log \frac{x}{m} & = \int_1^x \frac{1}{t} \left( \sum_{m \leqslant t} r_K(m) \right) \, \textrm{d}t \\ & \leqslant \sum_{j=0}^{n-1} \binom{n-1}{j} \frac{1}{j!} \int_1^x (\log t)^j \, \textrm{d}t \\ &= x \sum_{j=0}^{n-1} \binom{n-1}{j} (-1)^j \left\lbrace \sum_{k=0}^j \frac{(- \log x)^k}{k!} - \frac{1}{x} \right\rbrace \\ &= - x \sum_{j=0}^{n-1} \binom{n-1}{j} (-1)^j \sum_{k=j+1}^{\infty} \frac{(- \log x)^k}{k!} \\ &= - x \sum_{k=1}^{\infty} \frac{(- \log x)^k}{k!} \ \sum_{j=0}^{\min(n-1,k-1)} (-1)^j \binom{n-1}{j} \\ &= -x \sum_{k=1}^{\infty} (-1)^{k+\min(n-1,k-1)}\frac{(\log x)^k}{k!} \binom{n-2}{\min(n-1,k-1)} \\ &= x \sum_{k=1}^{n-1} \frac{(\log x)^k}{k!} \binom{n-2}{k-1} \\ & \leqslant \frac{x \log x}{(n-1)!} \left( \log x+ n -1\right)^{n-2}, \end{align*} $$
where we used [Reference Gould4, Identity (1.5)] in the
![]() $6$
th line, and the fact that, for
$6$
th line, and the fact that, for
![]() $0 \leqslant k \leqslant n-3$
,
$0 \leqslant k \leqslant n-3$
,
 $$ \begin{align*} \frac{1}{(k+1)!} &= \frac{1}{(n-1)!} \prod_{i=2}^{n-k-1} (i+k) \\ & \leqslant \frac{1}{(n-1)!} \left( \frac{1}{n-k-2} \sum_{i=2}^{n-k-1} (i+k) \right)^{n-k-2} \\ & \leqslant \frac{(n-1)^{n-k-2}}{(n-1)!} \end{align*} $$
$$ \begin{align*} \frac{1}{(k+1)!} &= \frac{1}{(n-1)!} \prod_{i=2}^{n-k-1} (i+k) \\ & \leqslant \frac{1}{(n-1)!} \left( \frac{1}{n-k-2} \sum_{i=2}^{n-k-1} (i+k) \right)^{n-k-2} \\ & \leqslant \frac{(n-1)^{n-k-2}}{(n-1)!} \end{align*} $$
by the GM–AM inequality stating that
![]() $\left ( a_1 \ldots a_N \right )^{1/N} \leqslant N^{-1} \left ( a_1 + \dotsb + a_N \right ) $
, where
$\left ( a_1 \ldots a_N \right )^{1/N} \leqslant N^{-1} \left ( a_1 + \dotsb + a_N \right ) $
, where
![]() $a_k> 0$
, and this bound also holds when
$a_k> 0$
, and this bound also holds when
![]() $k= n-2$
.
$k= n-2$
.
Lemma 2.4 If
![]() $n \geqslant 3$
,
$n \geqslant 3$
,
![]() $0 < \alpha < \frac {2}{n}$
and
$0 < \alpha < \frac {2}{n}$
and
![]() $\log C_K \geqslant \gamma _n$
, then
$\log C_K \geqslant \gamma _n$
, then
 $$ \begin{align*} \frac{\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \geqslant \frac{e^{\alpha(n-1)+1} \sqrt{\log C_K}}{\sqrt{\alpha(1-\alpha)}}. \end{align*} $$
$$ \begin{align*} \frac{\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \geqslant \frac{e^{\alpha(n-1)+1} \sqrt{\log C_K}}{\sqrt{\alpha(1-\alpha)}}. \end{align*} $$
Proof Squaring the inequality of the lemma, it is equivalent to show
The function
![]() $\alpha \in \left ( 0, \frac {2}{n} \right ) \mapsto \frac {\alpha ^{2n-5} e^{2\alpha (n-1)+2}}{1-\alpha }$
is nondecreasing, so that
$\alpha \in \left ( 0, \frac {2}{n} \right ) \mapsto \frac {\alpha ^{2n-5} e^{2\alpha (n-1)+2}}{1-\alpha }$
is nondecreasing, so that
and, therefore, it suffices to show
 $$ \begin{align*} \log C_K \geqslant 2 \left( \frac{e^{6-4/n}n^{6-2n}}{n-2} \right)^{\frac{1}{2n-5}} ((n-2)!)^{\frac{2}{2n-5}}. \end{align*} $$
$$ \begin{align*} \log C_K \geqslant 2 \left( \frac{e^{6-4/n}n^{6-2n}}{n-2} \right)^{\frac{1}{2n-5}} ((n-2)!)^{\frac{2}{2n-5}}. \end{align*} $$
Using Stirling’s bound, the inequality of the lemma is guaranteed as soon as
 $$ \begin{align*} \log C_K \geqslant 2 (2 \pi)^{\frac{1}{2n-5}} e^{- \frac{12n^3-84n^2+143n-48}{6n(n-2)(2n-5)}} \left( \frac{(n-2)^{2n-4}}{n^{2n-6}}\right)^{\frac{1}{2n-5}}, \end{align*} $$
$$ \begin{align*} \log C_K \geqslant 2 (2 \pi)^{\frac{1}{2n-5}} e^{- \frac{12n^3-84n^2+143n-48}{6n(n-2)(2n-5)}} \left( \frac{(n-2)^{2n-4}}{n^{2n-6}}\right)^{\frac{1}{2n-5}}, \end{align*} $$
and since the right-hand side is a nonincreasing function in
![]() $n \geqslant 3$
, it then suffices that
$n \geqslant 3$
, it then suffices that
![]() $\log C_K \geqslant s_n$
, where
$\log C_K \geqslant s_n$
, where
![]() and
and
![]() whenever
whenever
![]() $n \geqslant 4$
.
$n \geqslant 4$
.
3 Proof of the main result
By (1.1), it is sufficient to show that
 $$ \begin{align} \kappa_K < 3 \left( \frac{\left( \alpha^{-1} \log C_K \right)^{n-1}}{(n-1)!} - \frac{2\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \right). \end{align} $$
$$ \begin{align} \kappa_K < 3 \left( \frac{\left( \alpha^{-1} \log C_K \right)^{n-1}}{(n-1)!} - \frac{2\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \right). \end{align} $$
Assume
![]() $n \geqslant 3$
, and let
$n \geqslant 3$
, and let
![]() $0 < \delta < \alpha < \frac {2}{n}$
and
$0 < \delta < \alpha < \frac {2}{n}$
and
![]() $x \geqslant 1$
satisfying
$x \geqslant 1$
satisfying
and
By another Perron’s formula (see, for instance, [Reference Tenenbaum11, (2.9) p. 220]), we have
 $$ \begin{align*}\sum_{m \leqslant x} r_K (m) \log \frac{x}{m} = \frac{1}{2 \pi i} \int_{2-i \infty}^{2+i \infty} \frac{\zeta_K(s)}{s^2} \, x^s \, \textrm{d}s.\end{align*} $$
$$ \begin{align*}\sum_{m \leqslant x} r_K (m) \log \frac{x}{m} = \frac{1}{2 \pi i} \int_{2-i \infty}^{2+i \infty} \frac{\zeta_K(s)}{s^2} \, x^s \, \textrm{d}s.\end{align*} $$
Shifting the contour integration to the line
![]() $\sigma = 1 - \delta $
and picking up the residue of the integrand at the unique simple pole
$\sigma = 1 - \delta $
and picking up the residue of the integrand at the unique simple pole
![]() $s=1$
, we obtain by Cauchy’s theorem
$s=1$
, we obtain by Cauchy’s theorem
 $$ \begin{align*} \sum_{m \leqslant x} r_K (m) \log \frac{x}{m} & = \kappa_K x + \frac{1}{2 \pi i} \int_{1 - \delta-i \infty}^{1-\delta+i \infty} \frac{\zeta_K(s)}{s^2} \, x^s \, \textrm{d}s \\ & := \kappa_K x + I_{\delta} (x), \end{align*} $$
$$ \begin{align*} \sum_{m \leqslant x} r_K (m) \log \frac{x}{m} & = \kappa_K x + \frac{1}{2 \pi i} \int_{1 - \delta-i \infty}^{1-\delta+i \infty} \frac{\zeta_K(s)}{s^2} \, x^s \, \textrm{d}s \\ & := \kappa_K x + I_{\delta} (x), \end{align*} $$
and using Corollary 2.2, we get
 $$ \begin{align*} \left | I_{\delta} (x) \right | & \leqslant \frac{x^{1- \delta}}{2 \pi} \int_{- \infty}^{\infty} \frac{| \zeta_K ( 1 - \delta + it) |}{| 1-\delta + it |^2} \, \mathrm{d}t \\ & \leqslant \frac{x^{1-\delta}}{2\sqrt{1-\delta}} \left( \frac{\kappa_K}{\sqrt{\delta}} + \frac{C_K}{\sqrt{\alpha-\delta}} \right). \end{align*} $$
$$ \begin{align*} \left | I_{\delta} (x) \right | & \leqslant \frac{x^{1- \delta}}{2 \pi} \int_{- \infty}^{\infty} \frac{| \zeta_K ( 1 - \delta + it) |}{| 1-\delta + it |^2} \, \mathrm{d}t \\ & \leqslant \frac{x^{1-\delta}}{2\sqrt{1-\delta}} \left( \frac{\kappa_K}{\sqrt{\delta}} + \frac{C_K}{\sqrt{\alpha-\delta}} \right). \end{align*} $$
Therefore, using (3.2), we derive
 $$ \begin{align*} \sum_{m \leqslant x} r_K (m) \log \frac{x}{m} & \geqslant \kappa_K x \left( 1-\frac{x^{-\delta}}{2\sqrt{\delta (1-\delta)}}\right) -\frac{x^{1-\delta}}{2} \frac{C_K}{\sqrt{(1-\delta)(\alpha-\delta)}} \\ & \geqslant \frac{\kappa_K x}{2} -\frac{x^{1-\delta}}{2} \frac{C_K}{\sqrt{(1-\delta)(\alpha-\delta)}}, \end{align*} $$
$$ \begin{align*} \sum_{m \leqslant x} r_K (m) \log \frac{x}{m} & \geqslant \kappa_K x \left( 1-\frac{x^{-\delta}}{2\sqrt{\delta (1-\delta)}}\right) -\frac{x^{1-\delta}}{2} \frac{C_K}{\sqrt{(1-\delta)(\alpha-\delta)}} \\ & \geqslant \frac{\kappa_K x}{2} -\frac{x^{1-\delta}}{2} \frac{C_K}{\sqrt{(1-\delta)(\alpha-\delta)}}, \end{align*} $$
and Lemma 2.3 yields
 $$ \begin{align*} \kappa_K & \leqslant \frac{2}{x} \sum_{m \leqslant x} r_K (m) \log \frac{x}{m} + \frac{x^{-\delta}C_K}{\sqrt{(1-\delta)(\alpha-\delta)}} \\ & \leqslant \frac{2 \log x}{(n-1)!} \left( \log x+ n -1\right)^{n-2} + \frac{x^{-\delta}C_K}{\sqrt{(1-\delta)(\alpha-\delta)}}, \end{align*} $$
$$ \begin{align*} \kappa_K & \leqslant \frac{2}{x} \sum_{m \leqslant x} r_K (m) \log \frac{x}{m} + \frac{x^{-\delta}C_K}{\sqrt{(1-\delta)(\alpha-\delta)}} \\ & \leqslant \frac{2 \log x}{(n-1)!} \left( \log x+ n -1\right)^{n-2} + \frac{x^{-\delta}C_K}{\sqrt{(1-\delta)(\alpha-\delta)}}, \end{align*} $$
whenever x and
![]() $\delta $
satisfy (3.2). Now choose
$\delta $
satisfy (3.2). Now choose
Note that (3.2) is satisfied if
![]() $\left ( \alpha \log x - 1 \right ) \left (1 + (1-\alpha ) \log x \right ) \geqslant e^2 (\log x)^2 x^{-2\alpha }$
. But using (3.3), we get
$\left ( \alpha \log x - 1 \right ) \left (1 + (1-\alpha ) \log x \right ) \geqslant e^2 (\log x)^2 x^{-2\alpha }$
. But using (3.3), we get
Therefore, with the choice (3.4), we derive
 $$ \begin{align*} \kappa_K & \leqslant \frac{2 \log x}{(n-1)!} \left( \log x+ n -1\right)^{n-2} + \frac{e \, C_K x^{-\alpha} \log x}{\sqrt{(1-\alpha) \log x + 1}} \\ & < \frac{2 \log x}{(n-1)!} \left( \log x+ n -1\right)^{n-2} + \frac{e \, C_K x^{-\alpha} }{\sqrt{1-\alpha}} \sqrt{\log x} \end{align*} $$
$$ \begin{align*} \kappa_K & \leqslant \frac{2 \log x}{(n-1)!} \left( \log x+ n -1\right)^{n-2} + \frac{e \, C_K x^{-\alpha} \log x}{\sqrt{(1-\alpha) \log x + 1}} \\ & < \frac{2 \log x}{(n-1)!} \left( \log x+ n -1\right)^{n-2} + \frac{e \, C_K x^{-\alpha} }{\sqrt{1-\alpha}} \sqrt{\log x} \end{align*} $$
provided that (3.3) is fulfilled. We next choose
This yields
 $$ \begin{align*} \kappa_K & < 2 \left( \frac{\left( \alpha^{-1} \log C_K \right)^{n-1}}{(n-1)!} - \frac{\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \right) + \frac{e^{\alpha(n-1)+1} \sqrt{\log C_K + \alpha(1-n)}}{\sqrt{\alpha(1-\alpha)}} \\ & < 2 \left( \frac{\left( \alpha^{-1} \log C_K \right)^{n-1}}{(n-1)!} - \frac{\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \right) + \frac{e^{\alpha(n-1)+1} \sqrt{\log C_K}}{\sqrt{\alpha(1-\alpha)}}. \end{align*} $$
$$ \begin{align*} \kappa_K & < 2 \left( \frac{\left( \alpha^{-1} \log C_K \right)^{n-1}}{(n-1)!} - \frac{\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \right) + \frac{e^{\alpha(n-1)+1} \sqrt{\log C_K + \alpha(1-n)}}{\sqrt{\alpha(1-\alpha)}} \\ & < 2 \left( \frac{\left( \alpha^{-1} \log C_K \right)^{n-1}}{(n-1)!} - \frac{\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \right) + \frac{e^{\alpha(n-1)+1} \sqrt{\log C_K}}{\sqrt{\alpha(1-\alpha)}}. \end{align*} $$
Now, since
![]() $\log C_K \geqslant \gamma _n \geqslant 10> 10 - \frac {10}{n} \geqslant 5 \alpha (n-1)$
, we derive using Lemma 2.4
$\log C_K \geqslant \gamma _n \geqslant 10> 10 - \frac {10}{n} \geqslant 5 \alpha (n-1)$
, we derive using Lemma 2.4
 $$ \begin{align*} \frac{\left( \alpha^{-1} \log C_K \right)^{n-1}}{(n-1)!} - \frac{4\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} &= \frac{\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \left( \frac{\alpha^{-1}\log C_K}{n-1} - 4 \right) \\ &> \frac{\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \\ & \geqslant \frac{e^{\alpha(n-1)+1} \sqrt{\log C_K}}{\sqrt{\alpha(1-\alpha)}} \end{align*} $$
$$ \begin{align*} \frac{\left( \alpha^{-1} \log C_K \right)^{n-1}}{(n-1)!} - \frac{4\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} &= \frac{\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \left( \frac{\alpha^{-1}\log C_K}{n-1} - 4 \right) \\ &> \frac{\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \\ & \geqslant \frac{e^{\alpha(n-1)+1} \sqrt{\log C_K}}{\sqrt{\alpha(1-\alpha)}} \end{align*} $$
and, therefore,
 $$ \begin{align*} \kappa_K < 3 \left( \frac{\left( \alpha^{-1} \log C_K \right)^{n-1}}{(n-1)!} - \frac{2\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \right) \end{align*} $$
$$ \begin{align*} \kappa_K < 3 \left( \frac{\left( \alpha^{-1} \log C_K \right)^{n-1}}{(n-1)!} - \frac{2\left( \alpha^{-1} \log C_K \right)^{n-2}}{(n-2)!} \right) \end{align*} $$
which is (3.1). Now substituting this bound into (1.1) yields the desired result.
4 Example
Improving a result in Sunley’s thesis [Reference Sunley10], Lee [Reference Lee13] proved that, for all
![]() $x> 0,$
$x> 0,$
with
![]() . Hence, one can take
. Hence, one can take
![]() $\alpha = \frac {2}{n+1}$
and
$\alpha = \frac {2}{n+1}$
and
The hypothesis
![]() $\log C_K \geqslant \max \left ( \gamma _n \, , \, \alpha n + \frac {1}{4 \alpha ^2}\right )$
is easily fulfilled, and noticing that, for any
$\log C_K \geqslant \max \left ( \gamma _n \, , \, \alpha n + \frac {1}{4 \alpha ^2}\right )$
is easily fulfilled, and noticing that, for any
![]() $n \geqslant 3,$
$n \geqslant 3,$
we infer that Theorem 1.1 yields the following result.
Corollary 4.1 Let K be an algebraic number field of degree
![]() $n \geqslant 3$
. Then
$n \geqslant 3$
. Then
 $$ \begin{align*}h_K \mathcal{R}_K < \frac{3w_K}{2} \left( \frac{2}{\pi} \right)^{r_2} \left( \frac{\left (\tfrac{1}{4} \log d_K + L_K \right )^{n-1}}{(n-1)!} - \frac{\left (\tfrac{1}{4} \log d_K + \ell_K \right )^{n-2}}{(n-2)!} \right) d_K^{1/2},\end{align*} $$
$$ \begin{align*}h_K \mathcal{R}_K < \frac{3w_K}{2} \left( \frac{2}{\pi} \right)^{r_2} \left( \frac{\left (\tfrac{1}{4} \log d_K + L_K \right )^{n-1}}{(n-1)!} - \frac{\left (\tfrac{1}{4} \log d_K + \ell_K \right )^{n-2}}{(n-2)!} \right) d_K^{1/2},\end{align*} $$
where
 $\left. \begin {array}{c} L_K \\ \ell _K \end {array} \right \rbrace := \tfrac {1}{4} (n^2-1) \log \log d_K + \left \lbrace \begin {array}{c} 3 n^2 \log n \\ \frac {1}{2} n^2 \log n. \end {array} \right.$
$\left. \begin {array}{c} L_K \\ \ell _K \end {array} \right \rbrace := \tfrac {1}{4} (n^2-1) \log \log d_K + \left \lbrace \begin {array}{c} 3 n^2 \log n \\ \frac {1}{2} n^2 \log n. \end {array} \right.$
Note that Stirling’s bound yields
 $$ \begin{align*} h_K \mathcal{R}_K < \frac{3w_K}{2 \sqrt{2 \pi}} \left( \frac{2}{\pi} \right)^{r_2} \left\lbrace \frac{1}{\sqrt{n-1}} \left( \frac{e \log d_K}{4n-4} + \frac{e L_K}{n-1} \right)^{n-1} \right. \\ \left. - \frac{e^{-\frac{1}{12(n-2)}}}{\sqrt{n-2}} \left( \frac{e \log d_K}{4n-8} + \frac{e \ell_K}{n-2} \right)^{n-2} \right\rbrace d_K^{1/2} \end{align*} $$
$$ \begin{align*} h_K \mathcal{R}_K < \frac{3w_K}{2 \sqrt{2 \pi}} \left( \frac{2}{\pi} \right)^{r_2} \left\lbrace \frac{1}{\sqrt{n-1}} \left( \frac{e \log d_K}{4n-4} + \frac{e L_K}{n-1} \right)^{n-1} \right. \\ \left. - \frac{e^{-\frac{1}{12(n-2)}}}{\sqrt{n-2}} \left( \frac{e \log d_K}{4n-8} + \frac{e \ell_K}{n-2} \right)^{n-2} \right\rbrace d_K^{1/2} \end{align*} $$
which may be more easily compared to (1.2). It finally should be pointed out that Lee slightly improved in [Reference Lee6] the value of
![]() $C_K$
, showing that
$C_K$
, showing that
 $$ \begin{align*} C_K := \frac{0.54 \, (3n-1) \rho_K(n)}{(n-1)^2 (\log m_K)^{n-1}} \times n^{3/2} \times n! \end{align*} $$
$$ \begin{align*} C_K := \frac{0.54 \, (3n-1) \rho_K(n)}{(n-1)^2 (\log m_K)^{n-1}} \times n^{3/2} \times n! \end{align*} $$
with
![]() $m_K = (n^2 \pi /4)^{n} (n!)^{-2}$
and, if
$m_K = (n^2 \pi /4)^{n} (n!)^{-2}$
and, if
![]() $n> 13,$
$n> 13,$
Note that the author also gives the value of
![]() $\rho _K(n)$
in the range
$\rho _K(n)$
in the range
![]() $2 \leqslant n \leqslant 13$
. Although an improvement over the previous value of
$2 \leqslant n \leqslant 13$
. Although an improvement over the previous value of
![]() $C_K$
, this result is somewhat irrelevant on ours, while the calculations of
$C_K$
, this result is somewhat irrelevant on ours, while the calculations of
![]() $L_K$
and
$L_K$
and
![]() $\ell _K$
are more tedious.
$\ell _K$
are more tedious.
Acknowledgment
The author deeply acknowledges the anonymous referee for some corrections and remarks that have significantly enhanced the paper. The author also warmly thanks Stephan R. Garcia and Ethan S. Lee for sending him Sunley’s thesis [Reference Sunley10] and Lee’s preprint [Reference Lee13].