Introduction
Direct observation of floating or sinking phenomenon of living cells or biomolecules is an attractive research subject (Malkiel et al., Reference Malkiel, Alquaddoomi and Katz1999; Xiao et al., Reference Xiao, Li, Lam and Wang2012; Treguer et al., Reference Treguer, Bowler, Moriceau, Dutkiewicz, Gehlen, Aumont, Bittner, Dugdale, Finkel, Iudicone, Jahn, Guidi, Lasbleiz, Leblanc, Levy and Pondaven2018; Ide et al., Reference Ide, Matsukawa, Miyashiro, Mayama, Julius and Umemura2020; Shoumura et al., Reference Shoumura, Hamano, Hanada, Mayama and Umemura2020). The fluidity (or reciprocal of viscosity) refers to the ease with which fluids can flow, and in medical science, for example, the fluidity of cells and molecules is one of the important factors for human health from the perspective of body fluids that make up living organisms such as blood flow (Maher et al., Reference Maher, Kumeria, Aw and Losic2018). In nature, the floating and sinking of microorganisms such as photosynthetic plankton with respect to a reference point that is unrelated to the movement of water, such as the seabed, is an important parameter of cell proliferation (Armbrust, Reference Armbrust2009; Guiry, Reference Guiry2012; Malviya et al., Reference Malviya, Scalco, Audic, Vincenta, Veluchamy, Poulain, Wincker, Iudicone, de Vargas, Bittner, Zingone and Bowler2016). Growth also requires photosynthesis and nutrient uptake, which can be increased at low nutrient concentrations by faster movement through the water, which decreases the thickness of the diffusion boundary layer. In a few large diatoms that can switch between being denser than seawater and less dense than seawater, there is periodic vertical migration combining photosynthesis when near the surface with nutrient uptake when at the thermocline. As for loss factors, the enhanced sinking rate of infected cells might remove virally infected cells from the uninfected population and decrease the change of infection of infected cells. Increased sinking rate increases the chances of loss of cells from the upper mixed layer and hence the photic zone. Finally, sinking relates to the possibility of sexual reproduction in pennate diatoms (Raven & Waite, Reference Raven and Waite2004; Raven & Doblin, Reference Raven and Doblin2014; Font-Muñoz et al., Reference Font-Muñoz, Jeanneret, Arrieta, Anglès, Jordi, Tuval and Basterretxea2019). However, direct observation of the floating or sinking behaviors of cells and biomolecules by microscopes is not an easy topic.
Diatoms, one of the major photosynthetic planktons, live in various waters. The size of diatom cells is typically from several micrometer to several hundred micrometer (Moore & Villareal, Reference Moore and Villareal1996; Montagnes & Franklin, Reference Montagnes and Franklin2001; Snoeijs et al., Reference Snoeijs, Busse and Potapova2002). While many diatoms live in rivers, lakes, and seas, some of the species are found in hot springs (Owen et al., Reference Owen, Renaut and Jones2008). It is known that diatoms produce 20% of oxygen on the earth. It is also well known that optimal irradiation by sunlight is an important factor for their photosynthesis (Armbrust, Reference Armbrust2009; Guiry, Reference Guiry2012; Malviya et al., Reference Malviya, Scalco, Audic, Vincenta, Veluchamy, Poulain, Wincker, Iudicone, de Vargas, Bittner, Zingone and Bowler2016). Strong irradiation is not the best condition for diatom cells (Underwood & Kromkamp, Reference Underwood and Kromkamp1999; Armbrust, Reference Armbrust2009; Bowler et al., Reference Bowler, Vardi and Allen2010; Treguer et al., Reference Treguer, Bowler, Moriceau, Dutkiewicz, Gehlen, Aumont, Bittner, Dugdale, Finkel, Iudicone, Jahn, Guidi, Lasbleiz, Leblanc, Levy and Pondaven2018).
The specific weight of diatoms has been studied by several authors (Hansen et al., Reference Hansen, Hondzo, Sheng and Sadowsky2014; Aitken et al., Reference Aitken, Luo, Reynolds, Thaulow and Greer2016; Luo & Greer, Reference Luo and Greer2018). The value is slightly larger than that of water (Hansen et al., Reference Hansen, Hondzo, Sheng and Sadowsky2014; Aitken et al., Reference Aitken, Luo, Reynolds, Thaulow and Greer2016; Luo & Greer, Reference Luo and Greer2018). The density of seawater is 1,023 kg/m3 at 20°C and 33 g/L salinity, and diatom cells are 1,030−1,100 kg/m3 in the cytoplasm and 1,400−2,200 kg/m3 in the shell called the frustule (Miklasz & Denny, Reference Miklasz and Denny2010). Some species of diatom suspend in seawater, although some others attach to solid surfaces such as stones. In the case of floating diatoms, it is known that the stronger the waves and turbulence near the upper mixed layers of the seas or lakes, the faster the diatoms sink (Ruiz et al., Reference Ruiz, Macías and Peters2004).
Frustules are made of nanoporous silica (Nelson et al., Reference Nelson, Treguer, Brzezinski, Leynaert and Queguiner1995; Umemura et al., Reference Umemura, Liao, Mayama and Gad2007, Reference Umemura, Noguchi, Ichinose, Hirose, Kuroda and Mayama2008, Reference Umemura, Noguchi, Ichinose, Hirose and Mayama2010; Jang et al., Reference Jang, Meza, Greer and Greer2013; Maher et al., Reference Maher, Kumeria, Aw and Losic2018; Terracciano et al., Reference Terracciano, De Stefano and Rea2018) and are composed of 10–70% amorphous silica at a density of <2,600 kg/m3 and the balance being sugars and proteins with a density of <1,300 kg/m3 (Schmid et al., Reference Schmid, Borowitzka, Volcani and Kiermayer1981; Csögör et al., Reference Csögör, Melgar, Schmidt and Posten1999). With its unique 3D nanoporosity, the frustule optimizes diatom floating and sinking and diatom survival in water and helping to control photosynthesis, nutrient molecule selection, and antibacterial protection (Maher et al., Reference Maher, Kumeria, Aw and Losic2018).
When one wishes to observe the floating behavior of cells, particle imaging velocimetry (PIV) is one of the advanced methods. Several authors have observed the movement of suspended diatoms in water (Malkiel et al., Reference Malkiel, Alquaddoomi and Katz1999; Xiao et al., Reference Xiao, Li, Lam and Wang2012; Hansen et al., Reference Hansen, Hondzo, Sheng and Sadowsky2014). For example, Malkiel et al. (Reference Malkiel, Alquaddoomi and Katz1999) successfully observed 10–20 μm spherical particles and 3 μm linear particles using a homemade PIV system. Their purpose was to study the distribution of diatoms at various depths, not to measure the velocity of diatom motion. Xiao et al. (Reference Xiao, Li, Lam and Wang2012) observed aggregates of diatoms with their own PIV for their environmental studies. They estimated the settlement speed of the diatom aggregates. Hansen et al. (Reference Hansen, Hondzo, Sheng and Sadowsky2014) achieved comparison of fluid mechanical parameters for microorganisms, including diatoms, in the laboratory and in the field. PIV is a valuable and powerful method to study diatom behaviors in water; however, it is not similar to direct observation of individual cells by optical microscopy.
We have developed a “tumbled” optical microscope system (Shoumura et al., Reference Shoumura, Hamano, Hanada, Mayama and Umemura2020). A commercially available inverted microscope was tilted 90° using a homemade microscope stand. We named it a “tumbled” microscope. Then, the sample stage of the microscope became vertical with respect to the horizontal benchtop. When we mounted a sample, such as a sealed Petri dish with diatom cell suspension, we could directly observe the floating behavior of individual diatom cells in the microscope. This method is a kind of miniature aquarium. We can observe the swimming of fishes via small windows at an aquarium. In our method, we observe floating cells with the microscope system. Furthermore, we found that diatom floating was heavily affected by convection currents when we used a large vessel such as a Petri dish. Most of the cells floated to same directions. On the other hand, when a microchamber was employed, most of cells settled with constant speed. We also attached a heater to the sample stage in order to estimate effects of global warming. At higher temperature, the effects of convection currents were much larger (Ide et al., Reference Ide, Matsukawa, Miyashiro, Mayama, Julius and Umemura2020).
In this study, we compared four species diatoms in order to evaluate effects of sizes and shapes of the diatom cells on the settlement phenomenon of the diatom cells. For Nitzschia sp., the approximate lengths of the apical, transapical, and pervalvar axes were 45, 2.5, and 3.9 μm, respectively. For Pheodactylum tricornutum, the approximate lengths of the apical, transapical, and pervalvar axes were 23, 2.8, and 3.8 μm, respectively. For Navicula sp., the approximate lengths of the apical, transapical, and pervalvar axes were 31, 7.7, and 8.8 μm, respectively. For Odontella aurita, the approximate lengths of the apical, transapical, and pervalvar axes were 57, 9.2, and 10 μm, respectively.
Materials and Methods
For the isolated Nitzschia sp. (NIT), we used cells collected in Chiba Prefecture, Japan for the experiment. For the isolated P. tricornutum (PHE), we used cells provided by Laboratory Hanjia at Taiwan Ocean University. For the isolated Navicula sp. (NAV), we used cells collected in Shizuoka Prefecture, Japan. For the isolated O. aurita (ODO), we used cells purchased from NIES collection, National institute for Environmental Studies (Ibaraki, Japan). To subculture these cells, Guildard's (f/2) marine water enrichment solution (G9903; Sigma–Aldrich, Munich, Germany) was used. It was dissolved in 1,000 mL of pure water. Photosynthetic photon flux density was measured using a SpectroMaster C-7000 (SECONIC, Tokyo, Japan). The culture temperature was 21°C, and the culture was irradiated with a white fluorescent lamp of 85 μmol/m2/s1 for 12 h every day. For each subculture, 1 mL of diatom cells suspension was transferred to 10 mL of fresh culture solution. For the subculture, cycles were every 3 weeks for Nitzschia sp. and Navicula sp., every 1 week for P. tricornutum, every 4 weeks for O. aurita. Sizes and shapes of the diatom cells were observed by a holographic microscope (HT-2, Tomocube Inc., Deajeon, Korea).
The cells were observed using a homemade “tumbled” optical microscope system. This “tumbled” optical microscope is a commercial inverted microscope (CKX53; Olympus Co., Tokyo, Japan) tumbled by a homemade stand, and the vertical sample stage of the microscope is changed horizontally (Ide et al., Reference Ide, Matsukawa, Miyashiro, Mayama, Julius and Umemura2020; Shoumura et al., Reference Shoumura, Hamano, Hanada, Mayama and Umemura2020). Microscopic examination of the diatom suspension was performed approximately 10 days after the latest subculture.
A 1 mm3 microchamber was created by irradiation of the photosensitive chamber (FORTURN, Mainz, Germany) to a laser followed by wet etching (Hanada et al., Reference Hanada, Sugioka, Kawano, Ishikawa, Miyawaki and Midorikawa2008, Reference Hanada, Sugioka, Shihira-Ishikawa, Kawano, Miyawaki and Midorikawa2011). The fabricated microchamber was glued with a piece of Scotch tape (SWP-15; 3M, St. Paul, MN, USA) inside of the cover of a disposable Petri dish (52φ, 12 mm in thickness). The cover of another Petri dish was arranged with the upper part comprising the microchamber, and the bonding surface was hermetically sealed with parafilm. A quarter of the area of the composited Petri dishes was extracted to make a hole to inject a cell suspension.
The composited Petri dish was attached with a rubber band to the vertical sample stage of an “tumbled” microscope. The cell suspension was diluted 40-fold with medium, and 10 mL of the diluted cell suspension was injected into the composited Petri dish. Observations of diatom cells were initiated at room temperature using a 20× objective lens under 85 μmol/m2/s1 illumination and within 5 min of injection.
Observation movies of floating diatom cells were recorded for 1 h using a HDR-CX590 video camera (SONY, Tokyo, Japan) at a shutter speed of 1/30 s. The movies were recorded as AVCHD files. The resulting observation movies were analyzed using 2D tracking analysis software (Move-tr/2D, Library, Tokyo, Japan) (Umemura et al., Reference Umemura, Haneda, Tanabe, Suzuki, Kumashiro, Itoga, Okano and Mayama2013, Reference Umemura, Sadoya, Nagao, Oikawa, Hanada, Sugioka and Mayama2015). The movies were processed according to the following procedure. The movies were converted into WMV format, the image contrast was adapted using a background subtraction function, and calibration was made using an image of a scale.
Next, the images were analyzed by two methods. The first image analysis method was automatic analysis using the centroid mode. The centroid of each cell was automatically tracked every 0.03 s using software, and each centroid was acquired as a function of time (x(t), y(t)) in a two-dimensional rectangular coordinate system. To analyze the movement of diatom cells, 100 individuals were randomly selected for each type of diatom, and a total of the movement of 400 individuals were analyzed using four species of diatoms. The second image analysis method was a manual analysis performed to evaluate the rotation of each cell. Both ends of the cell were marked manually (major axis direction) every second, and the coordinates of the two points were recorded as a function of time (x 1(t), y 1(t)) and (x 2(t), y 2(t)). In the manual analysis, 10 individuals were randomly selected for each type of diatom, and the movement of a total of 40 individuals was analyzed using the four species of diatoms. In this two-point analysis, some characteristics of the motion—such as rotation and unrotation—were selected for the analysis.
The sinking speeds of diatom cells were simulated using the traditional Stokes’ law [equation (1)] and the modified Stokes’ law [(equation (2)] (Miklasz & Denny, Reference Miklasz and Denny2010).
 $$ {\matrix{ {U_{\rm M} = \displaystyle{{2g} \over {9\eta }}\left[{\matrix{ {\rho_{{\rm cyt}}\displaystyle{{{( {r-t_{\rm v}} ) }^2( {h_{\rm v}-t_{\rm v}} ) + {( {r-t_{\rm g}} ) }^2h_{\rm g}} \over {( {h_{\rm v} + h_{\rm g}} ) }}} \cr { + \rho_{{\rm ft}}\displaystyle{{r^2t_{\rm v} + t_{\rm v}( {h_{\rm v}-t_{\rm v}} ) ( {2r-t_{\rm v}} ) + h_{\rm g}t_{\rm g}( {2r-t_{\rm g}} ) } \over {( {h_{\rm v} + h_{\rm g}} ) }}-\rho_{\rm w}r^2} \cr } } \right]} \cr } , }$$
$$ {\matrix{ {U_{\rm M} = \displaystyle{{2g} \over {9\eta }}\left[{\matrix{ {\rho_{{\rm cyt}}\displaystyle{{{( {r-t_{\rm v}} ) }^2( {h_{\rm v}-t_{\rm v}} ) + {( {r-t_{\rm g}} ) }^2h_{\rm g}} \over {( {h_{\rm v} + h_{\rm g}} ) }}} \cr { + \rho_{{\rm ft}}\displaystyle{{r^2t_{\rm v} + t_{\rm v}( {h_{\rm v}-t_{\rm v}} ) ( {2r-t_{\rm v}} ) + h_{\rm g}t_{\rm g}( {2r-t_{\rm g}} ) } \over {( {h_{\rm v} + h_{\rm g}} ) }}-\rho_{\rm w}r^2} \cr } } \right]} \cr } , }$$where D p is the particle size when diatoms are assumed to be the same volume sphere, ρ tot = 1,800 kg/m3 is the total density of diatom cells, ρ w = 1,023 kg/m3 is the density of seawater at 25°C and 33 g/L salinity, g = 9.8 m/s2 is the gravitational acceleration, and η = 1.07 × 10−3 Pa·s is the dynamic viscosity of seawater at 25°C and 33 g/L salinity. Also, r is the radius of the cylindrical model, ρ cyt = 1,030 kg/m3 is the cytoplasmic density, ρ ft = 1,400 kg/m3 is the diatom shell density, and t v = t g = 1 μm is the shell thickness, and h v and h g are the heights. The variables used were values based on microscopic images (see Supplementary Fig. 1 and Table 1). Miklasz et al. focused on the difference in mass between diatom frustule and cytoplasm. It is assumed that the thickness of the frustule is constant regardless of the size of the diatom, the mass of the frustule is proportional to the surface area of the cell, and the mass of the cytoplasm is proportional to the volume. Therefore, the density of the entire cell is dominated by the density of the cytoplasm rather than the density of frustule, as the cell size increases. To reflect this fact in the calculations, Miklasz et al. proposed a modified Stokes’ law that separated the overall cell density into diatom frustule and cytoplasm.
Results and Discussions
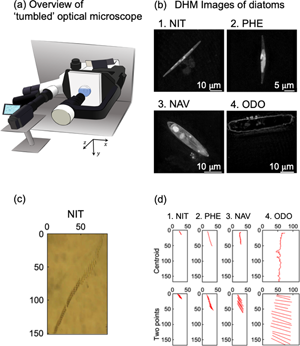
We evaluated sinking phenomena of four different diatom species by using our homemade optical microscope system. The “tumbled” optical microscope, which allows the sample stage to be tilted by 90°, is shown in Figure 1a. When a sample was attached on the tilted sample stage, sinking and floating phenomena of living cells and other micron size objects were observed. The sinking direction was defined as the y-axis. We have reported sinking phenomenon of Navicula sp. in a previous paper (Shoumura et al., Reference Shoumura, Hamano, Hanada, Mayama and Umemura2020). This time, we employed Nitzschia sp., P. tricornutum, Navicula sp., and O. aurita in order to understand effects of sizes and shapes of diatom cells on the sinking phenomena. For the approximate lengths of the apical, transapical, and pervalvar axes of NIT, PHE, NAV, and ODO, the average values of five individuals of four species of diatoms were recorded by digital holographic microscopy (DHM) observation (Fig. 1b; Umemura et al., Reference Umemura, Matsukawa, Ide and Mayama2020). By DHM observation, three-dimensional information of diatom cells was obtained without any pretreatment. The approximate lengths of the apical, transapical, and pervalvar axes were for NIT 45, 2.5, and 3.9 μm, respectively, for PHE 23, 2.8, and 3.8 μm, respectively, for NAV 31, 7.7, and 8.8 μm, respectively, and for ODO 57, 9.2, and 10 μm, respectively. The diatom cell shape was lanceolate for NIT and PHE, narrow elliptic for NAV, and cylindrical for ODO.
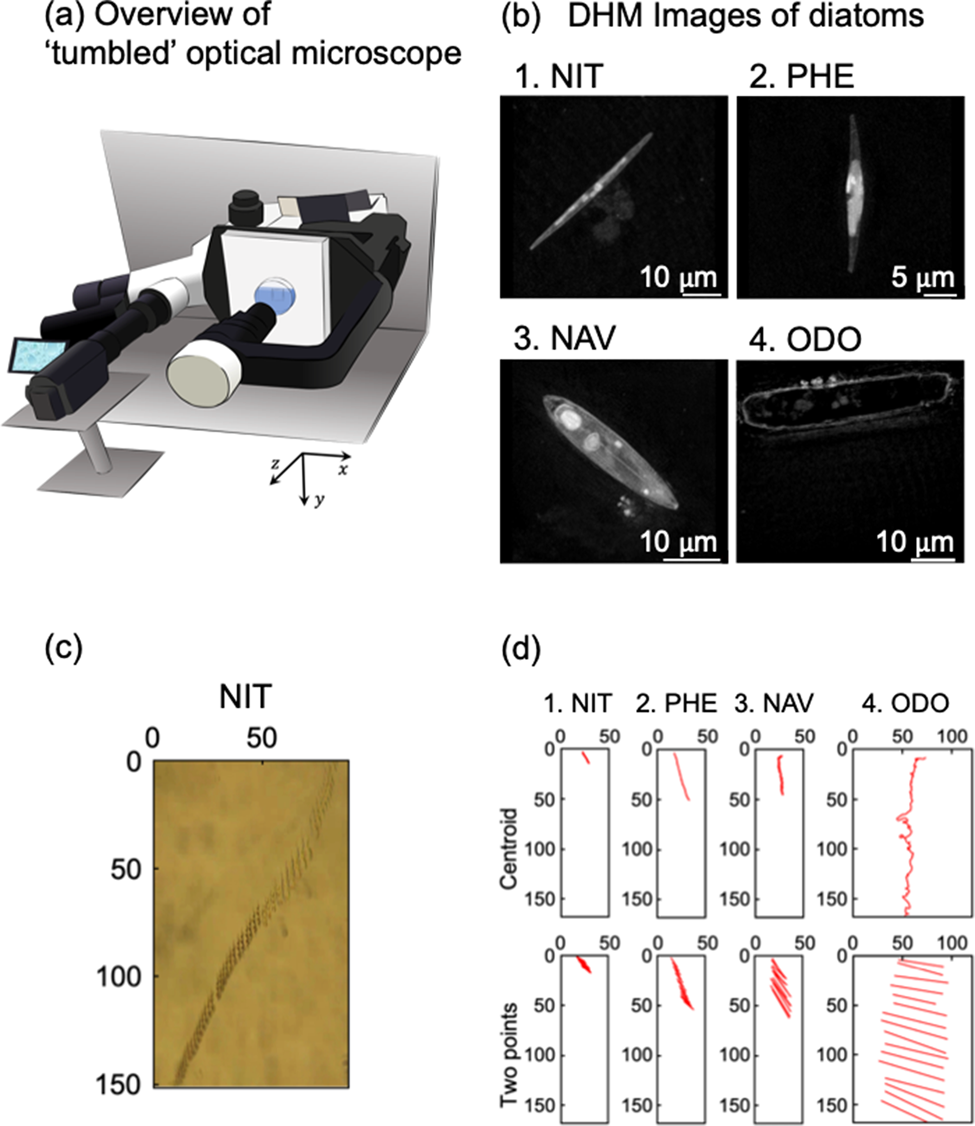
Fig. 1. (a) Schematic diagram of the “tumbled” optical microscope. (b) Microscopic image of diatoms by holographic microscope: (b-1) Nitzschia sp. (NIT), (b-2) P. tricornutum (PHE), (b-3) Navicula sp. (NAV), and (b-4) O. aurita (ODO). (c) Time-lapse of diatom cell (NIT) sedimentation taken with “tumbled” optical microscope. (d) 15-s trajectory diagram of diatom cells by automatic center of gravity analysis and manual two-point analysis: (d-1) NIT, (d-2) PHE, (d-3) NAV, and (d-4) ODO.
A typical example of sinking cells of NIT was indicated as Figure 1c. Cells were sunk at the middle area not along the basal surface of a microchamber (1 × 1 × 1 mm); therefore, the focus of the image was not perfect. However, the slender shape of the NIT cells was clearly visualized. As we described in our previous paper, perturbation of the culture medium was affected when we employed a Petri dish instead of the microchamber (Shoumura et al., Reference Shoumura, Hamano, Hanada, Mayama and Umemura2020). To observe sinking phenomena, the use of the microchamber is one of the key features of these experiments.
Figure 1d shows typical trajectories for sinking of the four species diatom cells during 15-s intervals, and it is obvious that ODO sank very quickly. It might be due the large size of the diatom cell. Sinking speed of NIZ was much slower than ODO. PHE and NAV were rather faster than NIT. In Figure 1d, we demonstrated two methods, “centroid” and “two points”, to obtain trajectories. In the “centroid” method, we used automatic analysis of the two-dimensional trajectory analysis software. The software automatically estimated centroid of each cell, and then, the trajectory of the centroids was obtained as numerical data. In the “two-point” method, we manually selected coordinates of two terminals of major axis of each cell (see Fig. 1d), and trajectories of the two terminals were obtained as numerical data. Because the two-point analysis were manually carried out, each coordinate was obtained every 1.00 s.
Table 1 shows numerical data of sinking speeds of the four species diatom cells obtained by the two-point analysis methods. Y-axis is the sinking direction. When the movies of diatom sinking were analyzed the automatic centroid method, average sinking speeds (v y) were 0.81 ± 5.56, 3.03 ± 10.17, 3.29 ± 7.39, and 11.22 ± 21.42 μm/s for NIZ, PHE, NAV, and ODO, respectively. The values were obtained with 2,995 fractions of five cells for each species. Velocities of lateral direction (v x) were almost zero in NIZ, PHE, and NAV, although it was 1.36 ± 26.26 μm/s in ODO. Note the huge standard deviation, this will be discussed later.
Table 1. Comparison of Experimental Velocity Values Obtained by Automatic Centroid Mode and Manual Two-Point Analysis with Velocity Values Calculated by Traditional and Modified Stokes’ law.

In addition, the n values of the automatic center of gravity analysis and the manual two-point method were 2,995 and 75 for each cell, respectively, and the obtained velocity values were almost similar in all cells. When assessing the movement of individual cells, the two-point analysis provided more information than the centroid analysis. From the coordinates of both ends of the elongated cell, it was possible to obtain, for example, the posture and rotation of diatoms at a certain time and the angular velocity.
Figure 2 revealed trajectories of movements of individual cells, which are analyzed by the centroid method (upper figures) and the two-point method (lower figures). In Figure 2, whole trajectories during the crossing observation area were delineated. Because sinking speeds were different due to cell species as discussed in Figure 1 and Table 1, time periods of each trajectory in Figure 2 were not uniform. Five cells were analyzed for each species. First, the trajectories of ODO obtained by the centroid method fluctuated markedly and were due to the fact that ODO was larger than NIT, PHE, and NAV; therefore, the coordinates of centroid of the cell could not be stably estimated. Although the sinking speed (v y) could be estimated even with the fluctuating data, precise analysis was impossible for ODO with the centroid analysis.

Fig. 2. Orbital analysis of five individual diatom cells of four species. The time intervals for automatic center of gravity analysis and manual two-point analysis are every 1 s and every 0.03 s, respectively. (a) NIT, (b) PHE, (c) NAV, and (d) ODO.
Figure 2a shows the trajectory of five individuals of NIT. On average, NIT took about 240 s to sink through the observation field. As can be seen from NIT-1, -2, and -4, there was a tendency for the sinking to occur, while there was significant movement in the x-axis direction. From the graph of the two-point analysis, it was found that they sank with almost no change in posture and without rotation.
Figure 2b shows the trajectories of five individuals of PHE. On average, PHE took about 130 s to sink the observation field. Regarding PHE-1 (1 means the cell number), the movement in the x-axis direction was large at the beginning, but the movement in the x-axis direction almost disappeared from the middle, and it settled perpendicular to the ground surface. For PHE-2 and PHE-3, these individuals had a small x-axis movement from the beginning. For PHE-4 and PHE-5, these individuals were moving across the x-axis field of view over the entire observation time. From the two-point analysis, PHE-4 in particular was settling while rotating continuously.
Figure 2c shows the trajectory of five individuals of NAV. On average, NAV took about 90 s to sink the observation field. Compared to NIT and PHE, NAV sank in all five individuals without much movement in the x-axis direction. From the two-point analysis, it should be noted that NAV-3 and -4 settled while rotating continuously.
Figure 2d shows the trajectory of five individuals with ODO. The ODO took about 30 s to sick, on average. As shown in Table 1, ODO was a diatom with a particularly fast settlement rate compared to NIT, PHE, and NAV. It should be noted that the orbit of the ODO obtained by the centroid method changed significantly. Due to the large size of the ODO, it was not possible to estimate the cell centroid coordinates in a stable manner. The settlement velocity (v y) could be estimated from the fluctuation data, but for ODO, the center of gravity analysis could not be used for accurate analysis. From the two-point analysis, it was found that ODO, like NIT, sank with almost no change in attitude until it disappeared from the observation field of view.
Rotation analysis of cells was available by the two-point method. In many cells, major axes of cell bodies were not exactly lateral, but stably sank without rotating. It suggests that the diatom cells do not indiscreetly rotate when perturbation of the culture medium is negligible. On the other hand, several cells always rotated during crossing the observation area. For example, the fourth cell of PHE (PHE-4), the third cell of NAV (NAV-3), and the fourth cell of NAV (NAV-4) in Figure 2 were rotating continuously. Figure 3 shows the time-lapse results of the angles of the three cells.
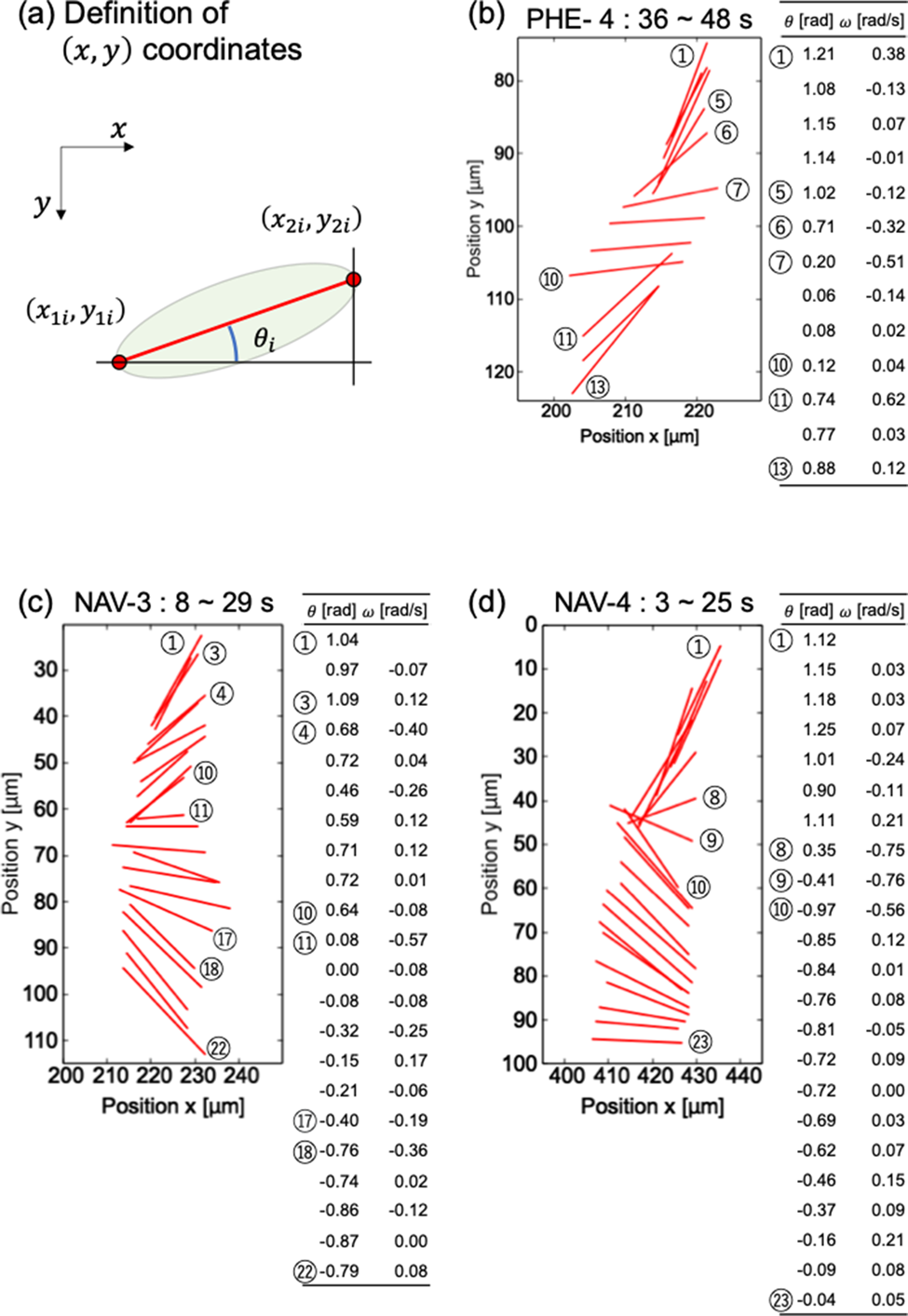
Fig. 3. Detailed analysis of diatom cell rotation phenomenon. (a) Definition of (x,y) coordinate. Magnified view of rotation and numerical analysis of diatom cells (b) PHE-4, (c) NAV-3, and (d) NAV-4.
Figures 3b–3d are enlarged graphs of Figure 2b for PHE-4 and 2c for NAV-3 and NAV-4, respectively. The angle θ with respect to the x-axis was calculated based on the definition in Figure 3a. The angular velocity ω was calculated by dividing the difference between the i + first angle and the ith angle by the measurement interval time (1 s). In Figure 3, ⑤–⑦ and ⑩–⑪ in (b), ③–④, ⑩–⑪, and ⑰–⑱ in (c), and ⑧–⑩ in (d) were a place to pay attention to the change in angle. As you can see in the table that summarizes the numerical values of the angle and the angular velocity, the magnitude of the change in the angle corresponds to the magnitude of the angular velocity. From Figure 3, it can be said that the angle of the diatom and the time change of the angle, which can be visually confirmed in the graph, are consistent with the table summarizing the numerical values obtained based on the coordinates.
To investigate whether the rotation method differs depending on the cell type, the average angular velocity was calculated for PHE-4, NAV-3, and NAV-4. The average angular velocities of PHE-4, NAV-3, and NAV-4 were −0.016 ± 0.22, −0.0090 ± 0.15, and 0.0044 ± 0.20 rad/s, respectively. There is no significant difference in the mean rotation angular velocity, which suggests that there may be no difference in diatom species in the way they rotate.
To understand the sinking phenomenon, which were experimentally observed by our unique microscopy methods, we demonstrated the following simulation analysis. For simplicity, the volume of diatom cells when approximated to a cylinder was estimated using dimensions obtained from microscopic images. Volumes of cells were 0.36, 0.20, 1.6, and 4.1 fm3 for NIZ, PHE, NAV, and ODO, respectively. First, we simulated using the traditional Stokes’ law [equation (1)]. This equation requires the assumption that the particle shape is a sphere. Therefore, the particle size (D P) was calculated as a sphere with the same volume as the volume of the obtained diatom (see Supplementary Table 1). The calculated sinking speeds (U S) of NIT, PHE, NAV, and ODO were 31, 21, 85, and 156 μm/s, respectively (see Table 1). Next, we simulated with the modified Stokes’ law [equation (2)]. This formula requires the assumption that the shape of the diatom is a cylinder. The radius r of the cylinder was determined based on the length of the diatom obtained by DHM (see Supplementary Table 1). The calculated sinking speeds U M of NIT, PHE, NAV, and ODO were 1.7, 1.8, 6.1, and 7.2 μm/s, respectively (see Table 1).
The experimental results were compared with the sinking speeds simulated from the obtained traditional/modified Stokes’ law. There were two points to note when comparing the simulation results and the experimental results. The first was the magnitude of the sinking speeds, and the second was the relationship between the volume of diatoms and the sinking speeds.
In the case of the magnitude of the velocity value, comparing the results of the traditional Stokes’ law U S with the experimental results (v y), the simulation results were calculated to be more than 10 times larger than the experimental results for all four species of diatoms. On the other hand, when comparing the results of the modified Stokes’ law (U M) with the experimental results, they were in agreement with the experimental values (v y) within the margin of error.
In the case of the relationship between the volume of diatoms and the sinking speeds, in the experimental results, the volume was larger in the order of PHE < NIT < NAV < ODO, and the sinking speeds (v y) was faster in the order of NIT < PHE < NAV < ODO. As a whole, the larger the volume, the faster the sinking speeds tended to be. The exception was that NIT had a slower settling velocity despite having a larger volume than PHE. In other words, the focus was on whether the simulation results could reproduce this NIT and PHE exception. The simulation result by traditional Stokes’ law (U S) is PHE < NIT < NAV < ODO, which could not explain the experimental result that NIT has a slower sinking speed than PHE. On the other hand, the simulation result (U M) by the modified Stokes’ law is NIT < PHE < NAV < ODO, which agrees with the experimental result.
The modified Stokes’ law, a model that separates frustule and cytoplasmic densities to reflect that the effect of cytoplasmic density is more dominant than frustule in proportion to the volume of diatoms, could well explain the results of this experiment. It was found that the sinking rate of diatoms largely depends on the shape and size of cells.
Conclusion
We observed and analyzed sinking phenomenon of four species of diatom cells using a “tumbled” light microscope, which was developed by our group. The use of microchamber was effective to minimize the effects of convection currents on diatom sinking; therefore, the obtained results could be discussed with simulations based on fluid dynamics. Direct observation of movements of individual cells will realize the better understanding of the photosynthetic efficiency of diatom cells circulating in water.
Supplementary Material
To view supplementary material for this article, please visit https://doi.org/10.1017/S1431927621012150.
Author contributions statement
The manuscript was written by R.H. and K.U. Experiments, including setup of the “tumbled” microscope, were performed by S.S. Microscopic images of diatom cells were provided by Y.T., T.Y., and K.H. The microchamber was fabricated by Y.H. The diatom cell identification and cell cultures were supported by S.M. The observations at DHM were supported by M.T. The acquisition and culture of diatom cells were supported by H.J.L. All data were verified and analyzed by R.H. Experiments were designed by K.U. All authors have given approval to the final version of the manuscript.
Funding
This work was supported by a Tokyo University of Science Grant for President's Research Promotion to M.T. and K.U. This work was supported by JST SICORP under Grant No. JPMJSC19E1, Japan. This work was supported by fellowship from Japan–Taiwan Exchange Association.