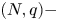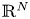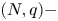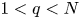1. Introduction and statement of main results
In 2015, M. Calanchi and B. Ruf have established a weighted Trudinger–Moser inequality in the unit ball $\mathcal {B}$![]() of $\mathbb {R}^N,\ N \geq 2.$
of $\mathbb {R}^N,\ N \geq 2.$![]() Such type of inequality is not new and many inequalities of Trudinger–Moser type defined in weighted Sobolev spaces have been proved; we can for example cite [Reference Abreu and Fernandez1–Reference Albuquerque3, Reference Aouaoui and Albuquerque5, Reference Calanchi13–Reference Calanchi and Ruf16, Reference de Oliveira and do Ò21, Reference do Ò and de Souza22, Reference Furtado, Medeiros and Severo26, Reference Lam29, Reference Nguyen and Takahashi33]. The majority of those works considered the restriction to radial functions, and in [Reference Lam29] although the weight is not necessarily radial but its growth permits to pass to the radial case through some radial rearrangement. This interest to reduce the inequality to the radial functions is mainly motivated by their ability to increase the maximal growth of the integrability. The weight that M. Calanchi and B. Ruf considered is of logarithmic type and turned out to be of great interest. More precisely, they introduced the subspace $W_{0,rad}^{1,N}(\mathcal {B}, \sigma _{\beta })$
Such type of inequality is not new and many inequalities of Trudinger–Moser type defined in weighted Sobolev spaces have been proved; we can for example cite [Reference Abreu and Fernandez1–Reference Albuquerque3, Reference Aouaoui and Albuquerque5, Reference Calanchi13–Reference Calanchi and Ruf16, Reference de Oliveira and do Ò21, Reference do Ò and de Souza22, Reference Furtado, Medeiros and Severo26, Reference Lam29, Reference Nguyen and Takahashi33]. The majority of those works considered the restriction to radial functions, and in [Reference Lam29] although the weight is not necessarily radial but its growth permits to pass to the radial case through some radial rearrangement. This interest to reduce the inequality to the radial functions is mainly motivated by their ability to increase the maximal growth of the integrability. The weight that M. Calanchi and B. Ruf considered is of logarithmic type and turned out to be of great interest. More precisely, they introduced the subspace $W_{0,rad}^{1,N}(\mathcal {B}, \sigma _{\beta })$![]() defined as the radial functions of the completion of $C_0^{\infty }(\mathcal {B})$
defined as the radial functions of the completion of $C_0^{\infty }(\mathcal {B})$![]() with respect to the norm
with respect to the norm
where $\sigma _{\beta }(x)=(\log \frac {1}{\left | x\right |})^{\beta (N-1)}$![]() or $\sigma _{\beta }(x)=(\log \frac {e}{\left | x\right |})^{\beta (N-1)}$
or $\sigma _{\beta }(x)=(\log \frac {e}{\left | x\right |})^{\beta (N-1)}$![]() , $0 < \beta \leq 1,\ x \in \mathcal {B}.$
, $0 < \beta \leq 1,\ x \in \mathcal {B}.$![]() In [Reference Calanchi and Ruf16, theorem 1], M. Calanchi and B. Ruf proved the following result: for $0 < \beta < 1,$
In [Reference Calanchi and Ruf16, theorem 1], M. Calanchi and B. Ruf proved the following result: for $0 < \beta < 1,$![]() we have
we have
•
(1.1)\begin{equation} \int_{\mathcal{B}}\,{\rm e}^{\left|u\right|^{\frac{N'}{1- \beta}}}\,{\rm d}x <{+} \infty,\ \forall\ u \in W_{0,rad}^{1,N}(\mathcal{B}, \sigma_{\beta}). \end{equation}
•
(1.2)\begin{equation} \sup\left\{\int_{\mathcal{B}}\,{\rm e}^{\alpha \left|u\right|^{\frac{N'}{1- \beta}}}\,{\rm d}x,\ u \in W^{1,N}_{0,rad}(\mathcal{B}, \sigma_{\beta}),\ \left\|u\right\|_{ \sigma_{\beta}} \leq 1\right\} <{+} \infty\Leftrightarrow\alpha \leq \alpha_{N,\beta}, \end{equation}where $\alpha _{N, \beta } =N[\omega _{N-1}^{\frac {1}{N-1}}(1-\beta )]^{\frac {1}{1-\beta }}$
 and $\omega _{N-1}$
and $\omega _{N-1}$ is the area of the unit sphere in $\mathbb {R}^N.$
is the area of the unit sphere in $\mathbb {R}^N.$
The case $N = 2$![]() has been considered in a previous work (see [Reference Calanchi and Ruf15]). Note that when $\beta = 0,$
has been considered in a previous work (see [Reference Calanchi and Ruf15]). Note that when $\beta = 0,$![]() (1.2) recovers the classical Trudinger–Moser inequality (see [Reference Moser31, Reference Trudinger38]). Next, M. Calanchi and B. Ruf considered the case when $\beta =1.$
(1.2) recovers the classical Trudinger–Moser inequality (see [Reference Moser31, Reference Trudinger38]). Next, M. Calanchi and B. Ruf considered the case when $\beta =1.$![]() In this case, the specific behaviour of the weight function has an impact on the corresponding embeddings. In fact, the maximal growth ${\rm e}^{\left |s\right |^{N'}}$
In this case, the specific behaviour of the weight function has an impact on the corresponding embeddings. In fact, the maximal growth ${\rm e}^{\left |s\right |^{N'}}$![]() proved in the classical Trudinger–Moser inequality significantly increased such that a doubly exponential growth is now permitted. More precisely, they proved the following result given in [Reference Calanchi and Ruf16, theorem 4]:
proved in the classical Trudinger–Moser inequality significantly increased such that a doubly exponential growth is now permitted. More precisely, they proved the following result given in [Reference Calanchi and Ruf16, theorem 4]:
•
(1.3)\begin{equation} \int_{\mathcal{B}}\,{\rm e}^{{\rm e}^{\left|u\right|^{N'}}}\,{\rm d}x<{+}\infty,\ \forall u\in W_{0,rad}^{1,N}(\mathcal{B}, \sigma_1),\ \text{where}\ \sigma_1(x) = \left(\log \frac{e}{\left|x\right|}\right)^{N-1}. \end{equation}
•
(1.4)\begin{equation} \sup\left\{\int_{\mathcal{B}}\,{\rm e}^{a\,{\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} | u|^{N'}}}\,{\rm d}x,\ u \in W_{0,rad}^{1,N}(\mathcal{B}, \sigma_1),\ \left\|u\right\|_{\sigma_1} \leq 1 \right\}<{+}\infty \Longleftrightarrow a\leq N. \end{equation}
The proof of (1.2) in the critical case $\alpha = \alpha _{N,\beta }$![]() is mainly based on a suitable change of variable combined to some integral inequality due to M.A. Leckband. In [Reference Nguyen34], V.H. Nguyen provided a simpler proof of (1.2) in which he proved that the function
is mainly based on a suitable change of variable combined to some integral inequality due to M.A. Leckband. In [Reference Nguyen34], V.H. Nguyen provided a simpler proof of (1.2) in which he proved that the function
is decreasing on $[0, 1).$![]() Moreover, V.H. Nguyen proved the existence of maximizer for this inequality when $\beta$
Moreover, V.H. Nguyen proved the existence of maximizer for this inequality when $\beta$![]() is sufficiently small. The question of the attainability of the inequality (1.2) has been also considered by P. Roy in [Reference Roy35] for the case $N = 2,$
is sufficiently small. The question of the attainability of the inequality (1.2) has been also considered by P. Roy in [Reference Roy35] for the case $N = 2,$![]() and in [Reference Roy36] for higher dimensions. Taking advantage of these new Trudinger–Moser inequalities defined on the unit ball $\mathcal {B}$
and in [Reference Roy36] for higher dimensions. Taking advantage of these new Trudinger–Moser inequalities defined on the unit ball $\mathcal {B}$![]() in $\mathbb {R}^N,$
in $\mathbb {R}^N,$![]() some authors studied an elliptic problem having a doubly exponential growth at infinity. It mainly consists in the following equation
some authors studied an elliptic problem having a doubly exponential growth at infinity. It mainly consists in the following equation

where the nonlinear term $f(x, u)$![]() is a continuous function, radial in $x\in \mathcal {B}$
is a continuous function, radial in $x\in \mathcal {B}$![]() and has a critical doubly exponential growth at infinity, which means that there exists a positive constant $\alpha _0$
and has a critical doubly exponential growth at infinity, which means that there exists a positive constant $\alpha _0$![]() such that
such that
M. Calanchi, B. Ruf and F. Sani proved in [Reference Calanchi, Ruf and Sani17] the existence of a nontrivial radial solution for the case $N = 2.$![]() This result has been recently generalized by C. Zhang in [Reference Zhang40] for higher dimensions. When we try to extend (1.1)–(1.4) to the whole Euclidean space $\mathbb {R}^N,\ N \geq 2,$
This result has been recently generalized by C. Zhang in [Reference Zhang40] for higher dimensions. When we try to extend (1.1)–(1.4) to the whole Euclidean space $\mathbb {R}^N,\ N \geq 2,$![]() we face many obstacles which mainly consist of the embedding and denseness properties of the functional space that we construct by extending the weight outside of the unit ball $\mathcal {B}.$
we face many obstacles which mainly consist of the embedding and denseness properties of the functional space that we construct by extending the weight outside of the unit ball $\mathcal {B}.$![]() For the first attempts, we worked with the weight $\sigma _{\beta }(x) = (\log \frac {e}{\left |x\right |})^{\beta (N-1)},\ \left |x\right | < 1.$
For the first attempts, we worked with the weight $\sigma _{\beta }(x) = (\log \frac {e}{\left |x\right |})^{\beta (N-1)},\ \left |x\right | < 1.$![]() In [Reference Aouaoui and Jlel6], we considered a radial weight $w_{\beta }$
In [Reference Aouaoui and Jlel6], we considered a radial weight $w_{\beta }$![]() defined by
defined by

where, $0 <\beta \leq 1$![]() and $\chi : [1, + \infty [ \rightarrow ]0, + \infty [$
and $\chi : [1, + \infty [ \rightarrow ]0, + \infty [$![]() is a continuous function such that $\chi (1) = 1,\ \displaystyle {\inf _{t \geq 1} \chi (t) > 0.}$
is a continuous function such that $\chi (1) = 1,\ \displaystyle {\inf _{t \geq 1} \chi (t) > 0.}$![]() Denoted by $Y_{\beta }$
Denoted by $Y_{\beta }$![]() the weighted Sobolev space
the weighted Sobolev space
and we equip it with the standard Sobolev norm
We obtained the following extensions of (1.1) and (1.2) to the whole space $\mathbb {R}^N:$![]() Let $N\geq 2$
Let $N\geq 2$![]() and $w_{\beta }$
and $w_{\beta }$![]() be defined by (1.5). Then, for all $\alpha >0$
be defined by (1.5). Then, for all $\alpha >0$![]() and $u \in Y_{\beta },$
and $u \in Y_{\beta },$![]() we have
we have
where

Moreover, if $\alpha < \alpha _{N,\beta }$![]() , then
, then

and if $\alpha > \alpha _{N,\beta }$![]() , then the supremum in (1.7) becomes infinite. For the value $\alpha = \alpha _{N,\beta },$
, then the supremum in (1.7) becomes infinite. For the value $\alpha = \alpha _{N,\beta },$![]() the supremum in (1.7) is not necessarily finite. However, the sharpness of the Trudinger–Moser inequality could be recovered by considering a different functional space. More precisely, for $0<\beta <1,$
the supremum in (1.7) is not necessarily finite. However, the sharpness of the Trudinger–Moser inequality could be recovered by considering a different functional space. More precisely, for $0<\beta <1,$![]() we define $Y_{\beta }'$
we define $Y_{\beta }'$![]() as the space of all the radial functions of the completion of $C_0^{\infty }(\mathbb {R}^N)$
as the space of all the radial functions of the completion of $C_0^{\infty }(\mathbb {R}^N)$![]() with respect to the norm
with respect to the norm

where $d'_{\beta }=\frac {N'(1-\beta )}{N'-1+\beta }.$![]() For that space, we obtained the following sharp Trudinger–Moser inequality which can be considered as another extension of (1.2): Let $0<\beta \leq \frac {1}{N'+1}$
For that space, we obtained the following sharp Trudinger–Moser inequality which can be considered as another extension of (1.2): Let $0<\beta \leq \frac {1}{N'+1}$![]() and $w_{\beta }$
and $w_{\beta }$![]() be defined by (1.5). Then,
be defined by (1.5). Then,

The value $\beta =1$![]() is a kind of second order limiting case. In [Reference Aouaoui and Jlel6], we established the following extension of (1.3) and (1.4):
is a kind of second order limiting case. In [Reference Aouaoui and Jlel6], we established the following extension of (1.3) and (1.4):
• For all $\alpha >0$
 and $u\in Y_1,$
and $u\in Y_1,$ there holds
(1.8)\begin{equation} \int_{\mathbb{R}^N}\left({\rm e}^{\alpha\left({\rm e}^{\left| u\right|^{N'}}-1\right)}-S_{N-2}\left( \alpha\left({\rm e}^{\left| u\right|^{N'}}-1\right)\right)\right){\rm d}x<{+}\infty. \end{equation}
there holds
(1.8)\begin{equation} \int_{\mathbb{R}^N}\left({\rm e}^{\alpha\left({\rm e}^{\left| u\right|^{N'}}-1\right)}-S_{N-2}\left( \alpha\left({\rm e}^{\left| u\right|^{N'}}-1\right)\right)\right){\rm d}x<{+}\infty. \end{equation}
• If $a\leq N\,{\rm e}^{-(\inf \limits _{s\geq 1}\chi (s))^{-\frac {1}{N(N-1)}}}$
 , then
(1.9)\begin{equation} \sup_{u\in Y_1,\ \left\| u\right\|_{Y_1}\leq1}\int_{\mathbb{R}^n}\left({\rm e}^{a\left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}\left| u\right|^{N'}}-1\right)}-S_{N-2}\left(a\left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}\left| u\right|^{N'}}-1\right)\right)\right){\rm d}x<{+}\infty. \end{equation}
, then
(1.9)\begin{equation} \sup_{u\in Y_1,\ \left\| u\right\|_{Y_1}\leq1}\int_{\mathbb{R}^n}\left({\rm e}^{a\left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}\left| u\right|^{N'}}-1\right)}-S_{N-2}\left(a\left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}\left| u\right|^{N'}}-1\right)\right)\right){\rm d}x<{+}\infty. \end{equation}
• If $\displaystyle a>N\exp \left (\frac {1}{N-1}\int _0^{+\infty }\log ^N(1+t)\,{\rm e}^{-Nt}\,{\rm d}t\right )$
 , then
(1.10)\begin{equation} \sup_{u\in Y_1,\ \left\| u\right\|_{Y_1}\leq 1}\int_{\mathbb{R}^N}\left({\rm e}^{a\left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}\left| u\right|^{N'}}-1\right)}-S_{N-2}\left(a\left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}\left| u\right|^{N'}}-1\right)\right)\right){\rm d}x={+}\infty. \end{equation}
, then
(1.10)\begin{equation} \sup_{u\in Y_1,\ \left\| u\right\|_{Y_1}\leq 1}\int_{\mathbb{R}^N}\left({\rm e}^{a\left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}\left| u\right|^{N'}}-1\right)}-S_{N-2}\left(a\left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}\left| u\right|^{N'}}-1\right)\right)\right){\rm d}x={+}\infty. \end{equation}
Note that the previous results come as generalizations of earlier works dealing with the case $N = 2.$![]() See [Reference Aouaoui4, Reference Aouaoui and Jlel7]. A further interesting extensions of (1.1)–(1.4) to the whole Euclidean space $\mathbb {R}^N$
See [Reference Aouaoui4, Reference Aouaoui and Jlel7]. A further interesting extensions of (1.1)–(1.4) to the whole Euclidean space $\mathbb {R}^N$![]() has been provided in [Reference Aouaoui and Jlel8, Reference Aouaoui and Jlel10].
has been provided in [Reference Aouaoui and Jlel8, Reference Aouaoui and Jlel10].
In this paper, we consider two types of weights. First, for the case when $0 < \beta < 1,$![]() we consider the weight defined by
we consider the weight defined by

where $\chi : [1, + \infty [ \rightarrow ]0, + \infty [$![]() is a continuous function such that $\chi (1) = 0.$
is a continuous function such that $\chi (1) = 0.$![]() Moreover, the function $\chi$
Moreover, the function $\chi$![]() is chosen such that $w_{\beta }$
is chosen such that $w_{\beta }$![]() satisfies (1.12), that is, $w_{\beta }$
satisfies (1.12), that is, $w_{\beta }$![]() belongs to the Muckenhoupt's class $A_N$
belongs to the Muckenhoupt's class $A_N$![]() (we also say that $w_{\beta }$
(we also say that $w_{\beta }$![]() is an $A_N-$
is an $A_N-$![]() weight), that is
weight), that is
where the supremum is taken over all balls $B$![]() in $\mathbb {R}^N.$
in $\mathbb {R}^N.$![]() The importance of this property of the weight $w_{\beta }$
The importance of this property of the weight $w_{\beta }$![]() lies in the fact that it implies that $C_{0}^{\infty }( \mathbb {R}^N)$
lies in the fact that it implies that $C_{0}^{\infty }( \mathbb {R}^N)$![]() is dense in the space $E_{\beta }$
is dense in the space $E_{\beta }$![]() (see, for instance, [Reference Cavalheiro18, Reference Kilpeläinen28, Reference Nakai, Tomita and Yabuta32] and references therein). An interesting example of such a function $\chi$
(see, for instance, [Reference Cavalheiro18, Reference Kilpeläinen28, Reference Nakai, Tomita and Yabuta32] and references therein). An interesting example of such a function $\chi$![]() is given by: $\chi (t) = \log ^{\gamma } (t),\ \gamma > 0$
is given by: $\chi (t) = \log ^{\gamma } (t),\ \gamma > 0$![]() (see [Reference Haroske27]). In particular, one can consider the weight
(see [Reference Haroske27]). In particular, one can consider the weight
That last weight can be seen as a natural extension of $(- \log \left |x\right |)^{\beta (N-1)}$![]() defined on $\mathcal {B} = \left \{x \in \mathbb {R}^N,\ \left |x\right | < 1\right \}$
defined on $\mathcal {B} = \left \{x \in \mathbb {R}^N,\ \left |x\right | < 1\right \}$![]() and considered in [Reference Calanchi and Ruf16]. Second, for the case $\beta = 1,$
and considered in [Reference Calanchi and Ruf16]. Second, for the case $\beta = 1,$![]() we consider the weight
we consider the weight

where $\chi : [1, + \infty [ \rightarrow ]0, + \infty [$![]() is a continuous function such that $\chi (1) = 1$
is a continuous function such that $\chi (1) = 1$![]() and $w_1$
and $w_1$![]() belongs to the Muckenhoupt's class $A_N.$
belongs to the Muckenhoupt's class $A_N.$![]() Here, are some examples of such a function $\chi.$
Here, are some examples of such a function $\chi.$![]()
• $\chi$
 can be any continuous and positive function such that $\chi (1) = 1$
can be any continuous and positive function such that $\chi (1) = 1$ and
\[ 0 < \inf_{t \geq 1} \chi(t) \leq \sup_{t \geq 1} \chi(t) <{+}\infty. \]
and
\[ 0 < \inf_{t \geq 1} \chi(t) \leq \sup_{t \geq 1} \chi(t) <{+}\infty. \]
• $\chi (t) = t^{\alpha },\ 0 < \alpha < N(N-1).$

• $\chi (t) = 1 + \log ^{\gamma } t,\ \gamma > 0.$

For details about these examples, we refer to [Reference Aouaoui and Jlel8]. Let $1 < q < N.$![]() For $0 < \beta \leq 1 ,$
For $0 < \beta \leq 1 ,$![]() denote by $E_{q,\beta }$
denote by $E_{q,\beta }$![]() the weighted Sobolev space
the weighted Sobolev space
where $D^{1,q}_r( \mathbb {R}^N) = \left \{u \in L^{q^*}( \mathbb {R}^N),\ u\ \text {radial},\ \displaystyle {\int _{\mathbb {R}^N} \left | \nabla u\right |^q\,{\rm d}x < + \infty }\right \}$![]() and $q^* = \frac {Nq}{N-q}.$
and $q^* = \frac {Nq}{N-q}.$![]() We first equip the functional space $E_{q,\beta }$
We first equip the functional space $E_{q,\beta }$![]() with the norm
with the norm

The first result in the present work concerns the case $0 < \beta < 1$![]() and the norm $\left \|\ \cdot \ \right \|_{E_{q,\beta }}.$
and the norm $\left \|\ \cdot \ \right \|_{E_{q,\beta }}.$![]() It is given by the following Trudinger–Moser inequality.
It is given by the following Trudinger–Moser inequality.
Theorem 1.1 Let $0 < \beta < 1$![]() and $w_{\beta }$
and $w_{\beta }$![]() be defined by (1.11). Let $j_{\beta } = \inf \left \{j \geq 1,\ j \geq \frac {(1- \beta )q^*}{N'}\right \}.$
be defined by (1.11). Let $j_{\beta } = \inf \left \{j \geq 1,\ j \geq \frac {(1- \beta )q^*}{N'}\right \}.$![]()
For all $\alpha >0$![]() and $u \in E_{q,\beta },$
and $u \in E_{q,\beta },$![]() we have
we have
where $\displaystyle {S_{j_{\beta }-1}(t) = \sum _{j=0}^{j_{\beta }-1} \frac {t^j}{j!},\ t \in [0, + \infty [.}$ Moreover, if $\alpha < \alpha _{N,\beta }$
Moreover, if $\alpha < \alpha _{N,\beta }$![]() , then
, then

and if $\alpha > \alpha _{N,\beta }$![]() , then
, then

The second result in this paper concerns the case $\beta = 1.$![]() More precisely, we prove the following theorem:
More precisely, we prove the following theorem:
Theorem 1.2 Let $w_1$![]() be defined by (1.13). Let $j_1 = \inf \left \{j \geq 1,\ j \geq \frac {q^*}{N'}\right \}.$
be defined by (1.13). Let $j_1 = \inf \left \{j \geq 1,\ j \geq \frac {q^*}{N'}\right \}.$![]() Set
Set

For all $\alpha >0$![]() and $u\in E_{q,1},$
and $u\in E_{q,1},$![]() we have
we have

where $\displaystyle { S_{j_{1}-1}(t) = \sum _{j=0}^{j_{1}-1} \frac {t^j}{j!},\ t \in [0, + \infty [.}$ Moreover, if $\alpha \leq N\,{\rm e}^{-\omega _{N-1}^{\frac {1}{N-1}} C_{q,N}^{N'}},$
Moreover, if $\alpha \leq N\,{\rm e}^{-\omega _{N-1}^{\frac {1}{N-1}} C_{q,N}^{N'}},$![]() then
then

and if

then

Note that the Trudinger–Moser inequalities proved in theorems 1.1 and 1.2 are not necessarily sharp. However, as we will see, this sharpness can be recovered when we consider another norm on the space $E_{q,\beta }$![]() equivalent to $\left \|\ \cdot \ \right \|_{E_{q,\beta }}$
equivalent to $\left \|\ \cdot \ \right \|_{E_{q,\beta }}$![]() and given by:
and given by:

and

The equivalence of this norm and $\left \|\ \cdot \ \right \|_{E_{q,\beta }}$![]() is proved below (see remark 1.8). Using the new norm $\left \|\ \cdot \ \right \|_{q,\beta },$
is proved below (see remark 1.8). Using the new norm $\left \|\ \cdot \ \right \|_{q,\beta },$![]() we can establish the following sharp Trudinger–Moser inequalities.
we can establish the following sharp Trudinger–Moser inequalities.
Theorem 1.3 Let $0 < \beta < 1$![]() and $w_{\beta }$
and $w_{\beta }$![]() be defined by (1.11). We have,
be defined by (1.11). We have,

Theorem 1.4 Let $w_1$![]() be defined by (1.13). We have,
be defined by (1.13). We have,

Comparing to previously cited works, there are many novelty aspects in the present work that we have to highlight. First, we are considering the case when the weight $w_{\beta },\ 0 < \beta < 1,$![]() vanishes at $x \in \mathbb {R}^N$
vanishes at $x \in \mathbb {R}^N$![]() such that $\left |x\right | = 1.$
such that $\left |x\right | = 1.$![]() In fact, as it was mentioned above, we did not consider such a case and we preferred take $w_{\beta } (x) = (1- \log \left |x\right |)^{\beta (N-1)},\ 0 < \left |x\right | < 1$
In fact, as it was mentioned above, we did not consider such a case and we preferred take $w_{\beta } (x) = (1- \log \left |x\right |)^{\beta (N-1)},\ 0 < \left |x\right | < 1$![]() in such a way that $\inf \limits _{x \in \mathbb {R}^N} w_{\beta }(x) > 0.$
in such a way that $\inf \limits _{x \in \mathbb {R}^N} w_{\beta }(x) > 0.$![]() The second aspect of novelty consists on taking only the gradient of the function to define the norms $\left \|\ \cdot \right \|_{E_{q,\beta }}$
The second aspect of novelty consists on taking only the gradient of the function to define the norms $\left \|\ \cdot \right \|_{E_{q,\beta }}$![]() and $\left \|\ \cdot \ \right \|_{q,\beta }.$
and $\left \|\ \cdot \ \right \|_{q,\beta }.$![]() The combination of the norms of the gradient in two different Lebesgue spaces which are $L^N_{w_{\beta }}( \mathbb {R}^N)$
The combination of the norms of the gradient in two different Lebesgue spaces which are $L^N_{w_{\beta }}( \mathbb {R}^N)$![]() and $L^q(\mathbb {R}^N)$
and $L^q(\mathbb {R}^N)$![]() has a real impact on the obtained inequalities. At this stage, we have to mention the work [Reference Carvalho, Figueiredo, Furtado and Medeiros19] in which the authors proved that
has a real impact on the obtained inequalities. At this stage, we have to mention the work [Reference Carvalho, Figueiredo, Furtado and Medeiros19] in which the authors proved that
and
where $1 < q < N,\ E^{N,q}$![]() is defined as the completion of $C_0^{\infty }( \mathbb {R}^N)$
is defined as the completion of $C_0^{\infty }( \mathbb {R}^N)$![]() with respect to the norm
with respect to the norm

and

So, we can clearly note that this result can be recovered when we take $\beta = 0$![]() in theorem 1.1. In other words, our present work can be partially seen as a generalization of [Reference Carvalho, Figueiredo, Furtado and Medeiros19] (when we choose $\chi \equiv 1$
in theorem 1.1. In other words, our present work can be partially seen as a generalization of [Reference Carvalho, Figueiredo, Furtado and Medeiros19] (when we choose $\chi \equiv 1$![]() ). But in contrast with [Reference Carvalho, Figueiredo, Furtado and Medeiros19], we are able here to establish the sharpness of the inequality by introducing the new norm $\left \|\ \cdot \ \right \|_{q,\beta }.$
). But in contrast with [Reference Carvalho, Figueiredo, Furtado and Medeiros19], we are able here to establish the sharpness of the inequality by introducing the new norm $\left \|\ \cdot \ \right \|_{q,\beta }.$![]() Obviously, this result of sharpness also holds for (1.23) provided that we pass from the norm $\left \|\ \cdot \ \right \|_{E^{N,q}}$
Obviously, this result of sharpness also holds for (1.23) provided that we pass from the norm $\left \|\ \cdot \ \right \|_{E^{N,q}}$![]() to the new one given by
to the new one given by

This leads us to the next point of novelty in the present work. It mainly consists on the sharpness of the inequalities (1.21) and (1.22). Actually, we have to highlight that such a sharp inequalities have been obtained in [Reference Aouaoui and Jlel9] for the case when $0< \beta < 1$![]() and its singular generalization proved in [Reference Aouaoui and Jlel11] for the case when $0 < \beta < 1$
and its singular generalization proved in [Reference Aouaoui and Jlel11] for the case when $0 < \beta < 1$![]() or even when $\beta = 1$
or even when $\beta = 1$![]() (i.e., for the doubly exponential growth case). In our present work and due to the existence of the term $\left | \nabla u\right |_{L^q( \mathbb {R}^N)},$
(i.e., for the doubly exponential growth case). In our present work and due to the existence of the term $\left | \nabla u\right |_{L^q( \mathbb {R}^N)},$![]() we are able to guarantee the same sharpness property of the inequalities for the both cases $0 < \beta < 1$
we are able to guarantee the same sharpness property of the inequalities for the both cases $0 < \beta < 1$![]() and also $\beta = 1.$
and also $\beta = 1.$![]() Finally, we establish an improvement of (1.15), (1.19), (1.21) and (1.22) for weakly convergent sequences in $E_{q,\beta },\ 0 < \beta \leq 1$
Finally, we establish an improvement of (1.15), (1.19), (1.21) and (1.22) for weakly convergent sequences in $E_{q,\beta },\ 0 < \beta \leq 1$![]() with constants larger than those found in (1.15), (1.19), (1.21), and (1.22). These results are completely new. Moreover, inequality (1.25) proved below is also an improvement of the inequality proved by J.L. Carvalho, G.M. Figueiredo, M.F. Furtado, and E. Medeiros in [Reference Carvalho, Figueiredo, Furtado and Medeiros19]. The proof of these new results is mainly based on some version of the Concentration-Compactness principle due to P.L. Lions in [Reference Lions30].
with constants larger than those found in (1.15), (1.19), (1.21), and (1.22). These results are completely new. Moreover, inequality (1.25) proved below is also an improvement of the inequality proved by J.L. Carvalho, G.M. Figueiredo, M.F. Furtado, and E. Medeiros in [Reference Carvalho, Figueiredo, Furtado and Medeiros19]. The proof of these new results is mainly based on some version of the Concentration-Compactness principle due to P.L. Lions in [Reference Lions30].
Theorem 1.5
1. Assume that $0 < \beta < 1.$
 Let $(u_n)_n \subset E_{q,\beta }$
Let $(u_n)_n \subset E_{q,\beta }$ and $u \in E_{q,\beta }{\setminus} {\left \{0\right \}}$
and $u \in E_{q,\beta }{\setminus} {\left \{0\right \}}$ be such that $\left \|u_n\right \|_{E_{q,\beta }} = 1$
be such that $\left \|u_n\right \|_{E_{q,\beta }} = 1$ and $u_n \rightharpoonup u$
and $u_n \rightharpoonup u$ weakly in $E_{q,\beta }.$
weakly in $E_{q,\beta }.$ Then,
(1.25)\begin{align} & \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{p \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(p \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}\right)\right)\,{\rm d}x\nonumber\\ & \quad <{+} \infty,\ \forall\ 0 < p < P_{N, \beta}(u), \end{align}where
Then,
(1.25)\begin{align} & \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{p \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(p \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}\right)\right)\,{\rm d}x\nonumber\\ & \quad <{+} \infty,\ \forall\ 0 < p < P_{N, \beta}(u), \end{align}where \[ P_{N, \beta}(u) = \left\{\begin{array}{ccc} \left(\dfrac{1}{1 - \left\|u\right\|_{E_{q,\beta}}^N}\right)^{\dfrac{1}{(1- \beta)(N-1)}}, & \text{if}\ \left\|u\right\|_{E_{q,\beta}} < 1, \\ + \infty, & \text{if}\ \left\|u\right\|_{E_{q,\beta}} = 1. \end{array} \right. \]Moreover, there exist a sequence $(u_n)_n \subset E_{q,\beta }$
\[ P_{N, \beta}(u) = \left\{\begin{array}{ccc} \left(\dfrac{1}{1 - \left\|u\right\|_{E_{q,\beta}}^N}\right)^{\dfrac{1}{(1- \beta)(N-1)}}, & \text{if}\ \left\|u\right\|_{E_{q,\beta}} < 1, \\ + \infty, & \text{if}\ \left\|u\right\|_{E_{q,\beta}} = 1. \end{array} \right. \]Moreover, there exist a sequence $(u_n)_n \subset E_{q,\beta }$
 and a function $u \in E_{q,\beta }{\setminus} {\left \{0\right \}}$
and a function $u \in E_{q,\beta }{\setminus} {\left \{0\right \}}$ satisfying $\left \|u_n\right \|_{E_{q,\beta }} = 1$
satisfying $\left \|u_n\right \|_{E_{q,\beta }} = 1$ and $u_n \rightharpoonup u$
and $u_n \rightharpoonup u$ weakly in $E_{q,\beta }$
weakly in $E_{q,\beta }$ such that
(1.26)\begin{equation} \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{p \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}} \!-\!S_{j_{\beta}-1}\left(p \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x \!=\!{+} \infty,\ \forall\ p \!>\! P_{N, \beta}(u). \end{equation}
such that
(1.26)\begin{equation} \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{p \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}} \!-\!S_{j_{\beta}-1}\left(p \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x \!=\!{+} \infty,\ \forall\ p \!>\! P_{N, \beta}(u). \end{equation}
2. Let $(u_n)_n \subset E_{q,1}$
 and $u \in E_{q,1}{\setminus} {\left \{0\right \}}$
and $u \in E_{q,1}{\setminus} {\left \{0\right \}}$ be such that $\left \|u_n\right \|_{E_{q,1}} = 1$
be such that $\left \|u_n\right \|_{E_{q,1}} = 1$ and $u_n \rightharpoonup u$
and $u_n \rightharpoonup u$ weakly in $E_{q,1}.$
weakly in $E_{q,1}.$ Then, for all $0 < p < P_{N,1}(u),$
Then, for all $0 < p < P_{N,1}(u),$ we have
(1.27)\begin{equation} \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p \left|u_n\right|^{N'}} -1\right)} \!-\!S_{j_1-1}\left(N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p \left|u_n\right|^{N'}} \!-\!1\right)\right)\right) {\rm d}x \!<\!{+} \infty, \end{equation}where
we have
(1.27)\begin{equation} \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p \left|u_n\right|^{N'}} -1\right)} \!-\!S_{j_1-1}\left(N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p \left|u_n\right|^{N'}} \!-\!1\right)\right)\right) {\rm d}x \!<\!{+} \infty, \end{equation}where \[ P_{N,1}(u) = \left\{\begin{array}{cc} \left(\dfrac{1}{1 - \left\|u\right\|_{E_{q,1}}^N}\right)^{\dfrac{1}{N-1}}, & \text{if}\ \left\|u\right\|_{E_{q,1}} < 1, \\ + \infty, & \text{if}\ \left\|u\right\|_{E_{q,1}} = 1. \end{array} \right. \]Moreover, there exist a sequence $(u_n)_n \subset E_{q,1}$
\[ P_{N,1}(u) = \left\{\begin{array}{cc} \left(\dfrac{1}{1 - \left\|u\right\|_{E_{q,1}}^N}\right)^{\dfrac{1}{N-1}}, & \text{if}\ \left\|u\right\|_{E_{q,1}} < 1, \\ + \infty, & \text{if}\ \left\|u\right\|_{E_{q,1}} = 1. \end{array} \right. \]Moreover, there exist a sequence $(u_n)_n \subset E_{q,1}$
 and a function $u \in E_{q,1}{\setminus} {\left \{0\right \}}$
and a function $u \in E_{q,1}{\setminus} {\left \{0\right \}}$ satisfying $\left \|u_n\right \|_{E_{q,1}} = 1$
satisfying $\left \|u_n\right \|_{E_{q,1}} = 1$ and $u_n \rightharpoonup u$
and $u_n \rightharpoonup u$ weakly in $E_{q,1}$
weakly in $E_{q,1}$ such that, for all $\alpha > 0$
such that, for all $\alpha > 0$ and $p > P_{N,1}(u),$
and $p > P_{N,1}(u),$ we have
(1.28)\begin{equation} \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{\alpha \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p \left|u_n\right|^{N'}} -1\right)} \!-\!S_{j_1-1}\left(\alpha \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p \left|u_n\right|^{N'}} \!-\!1\right)\right)\right) {\rm d}x \!=\!{+} \infty. \end{equation}
we have
(1.28)\begin{equation} \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{\alpha \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p \left|u_n\right|^{N'}} -1\right)} \!-\!S_{j_1-1}\left(\alpha \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p \left|u_n\right|^{N'}} \!-\!1\right)\right)\right) {\rm d}x \!=\!{+} \infty. \end{equation}
The next result concerns the norm $\left \|\ \cdot \ \right \|_{q,\beta },\ 0 < \beta \leq 1,$![]() and it consists in some improvements of the inequalities (1.21) and (1.22). At first glance and in a natural way, the reader is expecting to find that these improvements can be obtained by a simple change of the norm $\left \|\ \cdot \ \right \|_{E_{q,\beta }},\ 0 < \beta \leq 1$
and it consists in some improvements of the inequalities (1.21) and (1.22). At first glance and in a natural way, the reader is expecting to find that these improvements can be obtained by a simple change of the norm $\left \|\ \cdot \ \right \|_{E_{q,\beta }},\ 0 < \beta \leq 1$![]() which appears in the expression of $P_{N,\beta }(u)$
which appears in the expression of $P_{N,\beta }(u)$![]() in theorem 1.5 by $\left \|\ \cdot \ \right \|_{q,\beta }.$
in theorem 1.5 by $\left \|\ \cdot \ \right \|_{q,\beta }.$![]() But, due to the difference of the ‘geometric structure’ of the two norms, the situation is less easier than it seems.
But, due to the difference of the ‘geometric structure’ of the two norms, the situation is less easier than it seems.
Theorem 1.6
1. Assume that $0 < \beta < 1.$
 Let $(u_n)_n \subset E_{q,\beta }$
Let $(u_n)_n \subset E_{q,\beta }$ and $u \in E_{q,\beta }{\setminus} {\left \{0\right \}}$
and $u \in E_{q,\beta }{\setminus} {\left \{0\right \}}$ be such that $\left \|u_n\right \|_{q,\beta } = 1$
be such that $\left \|u_n\right \|_{q,\beta } = 1$ and $u_n \rightharpoonup u$
and $u_n \rightharpoonup u$ weakly in $E_{q,\beta }.$
weakly in $E_{q,\beta }.$ Then,
(1.29)\begin{align} & \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{p \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(p \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x\nonumber\\ & \quad <{+} \infty,\ \forall\ 0 < p < P_{N, \beta}(u), \end{align}where
Then,
(1.29)\begin{align} & \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{p \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(p \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x\nonumber\\ & \quad <{+} \infty,\ \forall\ 0 < p < P_{N, \beta}(u), \end{align}where \[ P_{N, \beta}(u) = \left\{\begin{array}{ll} \left(\dfrac{1}{1 - \left\|u\right\|_{q,\beta}^q}\right)^{\dfrac{N'}{q(1- \beta)}}, & \text{if}\ \left\|u\right\|_{q,\beta} < 1, \\ + \infty, & \text{if}\ \left\|u\right\|_{q,\beta} = 1. \end{array} \right. \]Moreover, there exist a sequence $(u_n)_n \subset E_{q,\beta }$
\[ P_{N, \beta}(u) = \left\{\begin{array}{ll} \left(\dfrac{1}{1 - \left\|u\right\|_{q,\beta}^q}\right)^{\dfrac{N'}{q(1- \beta)}}, & \text{if}\ \left\|u\right\|_{q,\beta} < 1, \\ + \infty, & \text{if}\ \left\|u\right\|_{q,\beta} = 1. \end{array} \right. \]Moreover, there exist a sequence $(u_n)_n \subset E_{q,\beta }$
 and a function $u \in E_{q,\beta }{\setminus} {\left \{0\right \}}$
and a function $u \in E_{q,\beta }{\setminus} {\left \{0\right \}}$ satisfying $\left \|u_n\right \|_{q ,\beta } = 1$
satisfying $\left \|u_n\right \|_{q ,\beta } = 1$ and $u_n \rightharpoonup u$
and $u_n \rightharpoonup u$ weakly in $E_{q,\beta }$
weakly in $E_{q,\beta }$ such that
(1.30)\begin{align} & \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{p \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(p \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}\right)\right)\nonumber\\ & \quad {\rm d}x ={+} \infty,\ \forall\ p > P_{N, \beta}(u). \end{align}
such that
(1.30)\begin{align} & \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{p \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(p \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}\right)\right)\nonumber\\ & \quad {\rm d}x ={+} \infty,\ \forall\ p > P_{N, \beta}(u). \end{align}
2. $\bullet$
 Let $(u_n)_n \subset E_{q,1}$
Let $(u_n)_n \subset E_{q,1}$ and $u \in E_{q,1}{\setminus} {\left \{0\right \}}$
and $u \in E_{q,1}{\setminus} {\left \{0\right \}}$ be such that $\left \|u_n\right \|_{q,1} = 1$
be such that $\left \|u_n\right \|_{q,1} = 1$ and $u_n \rightharpoonup u$
and $u_n \rightharpoonup u$ weakly in $E_{q,1}.$
weakly in $E_{q,1}.$ Then, for all $0 < p < P_{N,1}(u),$
Then, for all $0 < p < P_{N,1}(u),$ we have
(1.31)\begin{equation} \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p \left|u_n\right|^{N'}} -1\right)} \!-\!S_{j_1-1}\left(N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p \left|u_n\right|^{N'}} \!-\!1\right)\right)\right) {\rm d}x \!<\!{+} \infty, \end{equation}where
we have
(1.31)\begin{equation} \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p \left|u_n\right|^{N'}} -1\right)} \!-\!S_{j_1-1}\left(N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p \left|u_n\right|^{N'}} \!-\!1\right)\right)\right) {\rm d}x \!<\!{+} \infty, \end{equation}where \[ P_{N,1}(u) = \left\{\begin{array}{cc} \left(\dfrac{1}{1 - \left\|u\right\|_{q,1}^q}\right)^{\dfrac{N'}{q}}, & \text{if} \ \left\|u\right\|_{q,1} < 1, \\ + \infty, & \text{if} \ \left\|u\right\|_{q,1} = 1. \end{array}\right. \]Moreover, there exist a sequence $(u_n)_n \subset E_{q,1}$
\[ P_{N,1}(u) = \left\{\begin{array}{cc} \left(\dfrac{1}{1 - \left\|u\right\|_{q,1}^q}\right)^{\dfrac{N'}{q}}, & \text{if} \ \left\|u\right\|_{q,1} < 1, \\ + \infty, & \text{if} \ \left\|u\right\|_{q,1} = 1. \end{array}\right. \]Moreover, there exist a sequence $(u_n)_n \subset E_{q,1}$
 and a function $u \in E_{q,1}{\setminus} {\left \{0\right \}}$
and a function $u \in E_{q,1}{\setminus} {\left \{0\right \}}$ satisfying $\left \|u_n\right \|_{q,1} = 1$
satisfying $\left \|u_n\right \|_{q,1} = 1$ and $u_n \rightharpoonup u$
and $u_n \rightharpoonup u$ weakly in $E_{q,1}$
weakly in $E_{q,1}$ such that, for all $\alpha > 0$
such that, for all $\alpha > 0$ and $p > P_{N,1}(u),$
and $p > P_{N,1}(u),$ we have
(1.32)\begin{equation} \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{\alpha \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p \left|u_n\right|^{N'}} -1\right)} \!-\!S_{j_1-1}\left(\alpha \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p \left|u_n\right|^{N'}} \!-\!1\right)\right)\right) {\rm d}x \!=\!{+} \infty. \end{equation}
we have
(1.32)\begin{equation} \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{\alpha \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p \left|u_n\right|^{N'}} -1\right)} \!-\!S_{j_1-1}\left(\alpha \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p \left|u_n\right|^{N'}} \!-\!1\right)\right)\right) {\rm d}x \!=\!{+} \infty. \end{equation}
Remark 1.7 Obviously, all the results obtained for the weight $w_{\beta }$![]() given by (1.11) hold true when we take
given by (1.11) hold true when we take
where $\chi : [1, + \infty [ \rightarrow ]0, + \infty [$![]() is a continuous function such that $\chi (1) = 1$
is a continuous function such that $\chi (1) = 1$![]() and $w_{\beta } \in A_N.$
and $w_{\beta } \in A_N.$![]()
In the last part of this work, we apply the Trudinger–Moser inequalities established in theorem 1.2 to study some elliptic quasilinear equation defined in $\mathbb {R}^N$![]() and containing a nonlinearities having a doubly exponential growth at infinity. More precisely, we prove the existence of at least one nontrivial solution to the equation
and containing a nonlinearities having a doubly exponential growth at infinity. More precisely, we prove the existence of at least one nontrivial solution to the equation
where $f : \mathbb {R} \rightarrow \mathbb {R}$![]() is a continuous function enjoying a doubly exponential growth at infinity governed by the inequality (1.22). In the mathematical literature, the first equation involving an operator with non-standard growth of the type $(p, N)-$
is a continuous function enjoying a doubly exponential growth at infinity governed by the inequality (1.22). In the mathematical literature, the first equation involving an operator with non-standard growth of the type $(p, N)-$![]() Laplacian with $0 < p < N$
Laplacian with $0 < p < N$![]() appeared in [Reference Yang and Perera39] where the problem was studied in a bounded domain and where the nonlinear term has an exponential growth governed by the classical Trudinger–Moser inequality. In [Reference Yang and Perera39], the authors obtained an existence result via a suitable minimax argument. This work was followed by [Reference Figueiredo and Nunes24] where the Nehari manifold approach has been used to obtain an existence result always by assuming the boundedness of the domain. For equations in the entire space, we can quote the following recent works [Reference Carvalho, Figueiredo, Furtado and Medeiros19, Reference Chen, Fiscella, Pucci and Tang20, Reference Fiscella and Pucci25] which deal with exponential growth governed by classical non-weighted Trudinger–Moser inequality.
appeared in [Reference Yang and Perera39] where the problem was studied in a bounded domain and where the nonlinear term has an exponential growth governed by the classical Trudinger–Moser inequality. In [Reference Yang and Perera39], the authors obtained an existence result via a suitable minimax argument. This work was followed by [Reference Figueiredo and Nunes24] where the Nehari manifold approach has been used to obtain an existence result always by assuming the boundedness of the domain. For equations in the entire space, we can quote the following recent works [Reference Carvalho, Figueiredo, Furtado and Medeiros19, Reference Chen, Fiscella, Pucci and Tang20, Reference Fiscella and Pucci25] which deal with exponential growth governed by classical non-weighted Trudinger–Moser inequality.
Remark 1.8 We can easily show that, for $0 < \beta \leq 1,$![]() the norms $\left \|\ \cdot \ \right \|_{q,\beta }$
the norms $\left \|\ \cdot \ \right \|_{q,\beta }$![]() and $\left \|\ \cdot \ \right \|_{E_{q,\beta }}$
and $\left \|\ \cdot \ \right \|_{E_{q,\beta }}$![]() are equivalent. The case when $0 < \beta < 1$
are equivalent. The case when $0 < \beta < 1$![]() is rather evident, we only prove the equivalence of the norms when $\beta = 1.$
is rather evident, we only prove the equivalence of the norms when $\beta = 1.$![]() For that aim, let $u \in E_{q,1}.$
For that aim, let $u \in E_{q,1}.$![]() We have
We have

Since $\displaystyle { \int _0^1 (1- \log r)^{-q(N-1)/N-q} r^{N-1}\,{\rm d}r < + \infty,}$![]() then $\displaystyle {\int _{\left |x\right | < 1} w_1^{-q/N-q}\,{\rm d}x < + \infty.}$
then $\displaystyle {\int _{\left |x\right | < 1} w_1^{-q/N-q}\,{\rm d}x < + \infty.}$![]() Consequently, there exists a positive constant $M_0$
Consequently, there exists a positive constant $M_0$![]() such that
such that

Thus,

Now, using the following elementary inequality,
we infer from (1.33) that

Hence,

Now, having in mind that

by (1.34) we obtain
On the other hand, taking into account that the function $x \longmapsto x^{\frac {1}{N}}$![]() is concave on $[0, + \infty [,$
is concave on $[0, + \infty [,$![]() we get
we get
It follows that,

Combining that last inequality with (1.35), we deduce that
Remark 1.9 A pertinent question is why when $\beta = 1,$![]() we change the form of the norm $\left \|\ \cdot \ \right \|_{q,1}$
we change the form of the norm $\left \|\ \cdot \ \right \|_{q,1}$![]() by taking only the integral over the set $\left \{x \in \mathbb {R}^N,\ \left |x\right | \geq 1 \right \}.$
by taking only the integral over the set $\left \{x \in \mathbb {R}^N,\ \left |x\right | \geq 1 \right \}.$![]() In fact, one can naturally expect that this last norm takes the form
In fact, one can naturally expect that this last norm takes the form

Taking that last norm, we can easily adapt the proof of theorem 1.4 to prove that, if $\alpha \leq N,$![]() then
then

The problem lies in the construction of a sequence (if there exists) $(u_k)_k \subset E_{q,1}$![]() such that $\left \|u_k\right \|_{q,1}^{(1)} \leq 1$
such that $\left \|u_k\right \|_{q,1}^{(1)} \leq 1$![]() and
and

We do not know the existence of such a sequence.
2. Proof of theorem 1.1
We start by proving (1.14). For that aim, fix $\alpha > 0$![]() and $u \in E_{q,\beta }.$
and $u \in E_{q,\beta }.$![]() We have
We have

On the one hand, we have

Since $u$![]() belongs to $D^{1,q}_r(\mathbb {R}^N),$
belongs to $D^{1,q}_r(\mathbb {R}^N),$![]() then by the radial lemma (see [Reference Su, Wang and Willem37, lemma 1]), we know that
then by the radial lemma (see [Reference Su, Wang and Willem37, lemma 1]), we know that
where $C_{q,N}$![]() is given by (1.17). For $j \geq j_{\beta },$
is given by (1.17). For $j \geq j_{\beta },$![]() we have $\frac {jN'}{1- \beta } \geq q^*.$
we have $\frac {jN'}{1- \beta } \geq q^*.$![]() By (2.3), it yields
By (2.3), it yields
By (2.4), we infer

where we used the continuous embedding $D^{1,q}_r( \mathbb {R}^N) \hookrightarrow L^{q^*}( \mathbb {R}^N).$![]() Putting (2.5) in (2.2), we obtain
Putting (2.5) in (2.2), we obtain

Now, in order to estimate the second integral in (2.1), set
where $e_1= (1,0,\cdots,0)$![]() is the first vector in the canonical basis of $\mathbb {R}^N.$
is the first vector in the canonical basis of $\mathbb {R}^N.$![]() Clearly, $v \in W^{1,N}_{0,rad}(\mathcal {B},\sigma _{\beta }),$
Clearly, $v \in W^{1,N}_{0,rad}(\mathcal {B},\sigma _{\beta }),$![]() with $\sigma _{\beta }(x) = (- \log \left |x\right |)^{\beta (N-1)},\ x \in \mathcal {B}.$
with $\sigma _{\beta }(x) = (- \log \left |x\right |)^{\beta (N-1)},\ x \in \mathcal {B}.$![]() An elementary calculus gives the following inequality: for all $\epsilon >0$
An elementary calculus gives the following inequality: for all $\epsilon >0$![]() , we have
, we have

Fix $0 < \epsilon < 1.$![]() By (2.8), we get
By (2.8), we get

By (1.1), we know that

and by consequence (2.9) leads to

Combining (2.10) and (2.6), we deduce that (1.14) holds.
Now, we prove (1.15). By (2.6), it yields

Next, let $\alpha < \alpha _{N,\beta }.$![]() Clearly, there exists $\epsilon > 0$
Clearly, there exists $\epsilon > 0$![]() such that $\alpha (1+ \epsilon ) < \alpha _{N,\beta }.$
such that $\alpha (1+ \epsilon ) < \alpha _{N,\beta }.$![]() Let $u \in E_{q, \beta }$
Let $u \in E_{q, \beta }$![]() be such that $\left \|u\right \|_{E_{q,\beta }} \leq 1.$
be such that $\left \|u\right \|_{E_{q,\beta }} \leq 1.$![]() Having in mind that $v$
Having in mind that $v$![]() defined by (2.7) belongs to $W^{1,N}_{0,rad}(\mathcal {B}, \sigma _{\beta })$
defined by (2.7) belongs to $W^{1,N}_{0,rad}(\mathcal {B}, \sigma _{\beta })$![]() and
and
then, by the virtue of (1.2), we infer that there exists a positive constant $C_{\beta } > 0$![]() such that
such that

Moreover, by (2.3), we know that $\left |u(e_1)\right | \leq C_{q,N}.$![]() Hence, by (2.9) and (2.12) we obtain
Hence, by (2.9) and (2.12) we obtain

Combining (2.13) and (2.11), we deduce that (1.15) holds.
For $u \in E_{q,\beta },$![]() set $\psi (t) = \omega _{N-1}^{\frac {1}{N}} u(x)$
set $\psi (t) = \omega _{N-1}^{\frac {1}{N}} u(x)$![]() with $\left |x\right | = {\rm e}^{-t},\ t \in \mathbb {R}.$
with $\left |x\right | = {\rm e}^{-t},\ t \in \mathbb {R}.$![]() A direct computation gives:
A direct computation gives:

and

Let $\gamma > 0$![]() to be fixed later. Consider the sequence of test functions:
to be fixed later. Consider the sequence of test functions:

For $k \geq 1,$![]() define $u_k \in E_{q,\beta }$
define $u_k \in E_{q,\beta }$![]() by $\psi _k(t) = \omega _{N-1}^{\frac {1}{N}} u_k(x),\ \left |x\right | = {\rm e}^{-t},\ t \in \mathbb {R}.$
by $\psi _k(t) = \omega _{N-1}^{\frac {1}{N}} u_k(x),\ \left |x\right | = {\rm e}^{-t},\ t \in \mathbb {R}.$![]() We have
We have


Choosing $\gamma$![]() small enough such that $( \beta -1)(\gamma + \frac {1}{N}) + \gamma < 0.$
small enough such that $( \beta -1)(\gamma + \frac {1}{N}) + \gamma < 0.$![]() By this choice, we get
By this choice, we get
On the other hand,
Thus, by (2.15), we infer
Now, taking into account that $(\beta -1)( \gamma +1) < 0,$![]() it follows from (2.14) that
it follows from (2.14) that
Hence,

Set $\widetilde {u_k} = \frac {u_k}{\left \|u_k\right \|_{E_{q,\beta }}}.$![]() For $\alpha > 0,$
For $\alpha > 0,$![]() we have
we have

Clearly, for $0 \leq j \leq j_{\beta }-1,$![]() we have
we have

Thus,

Moreover,

Having in mind that $\left \|u_k\right \|_{E_{q,\beta }} \to (1- \beta )^{1/N'},$![]() then
then

If $\alpha > \alpha _{N,\beta },$![]() then
then

Consequently,

Combining (2.18) and (2.17), we deduce from (2.16) that

We conclude that (1.16) holds.
3. Proof of theorem 1.2
Let $\alpha > 0$![]() and $u \in E_{q,1}.$
and $u \in E_{q,1}.$![]() We have
We have

Using the monotony of the function defined on $[0, + \infty [$![]() by $s \longmapsto \frac {e^s -1}{s},$
by $s \longmapsto \frac {e^s -1}{s},$![]() from (2.3) it yields
from (2.3) it yields

Observe that $j \geq j_1 \Leftrightarrow jN' \geq q^{*}.$![]() Thus, for $j \geq j_1,$
Thus, for $j \geq j_1,$![]() we have
we have

Putting that last inequality in (3.1), we infer

Next, by (2.8) one can easily deduce the following inequality:

By (3.3), we have

where $v$![]() is given by (2.7). Thus,
is given by (2.7). Thus,

Clearly, $v \in W^{1,N}_{0,rad}(\mathcal {B},\sigma _{1}).$![]() By (1.3) and (3.4), it follows
By (1.3) and (3.4), it follows
Combining (3.5) and (3.2), we easily see that (1.18) holds.
The next step in the proof of theorem 1.2 consists of proving (1.19). First, observe that by (3.2), we have

Let $u \in E_{q,1}$![]() be such that $\left \|u\right \|_{E_{q,1}} \leq 1.$
be such that $\left \|u\right \|_{E_{q,1}} \leq 1.$![]() Note that if $\displaystyle { \int _{\left |x\right | < 1} \left | \nabla u\right |^N w_{1}(x)\,{\rm d}x = 1,}$
Note that if $\displaystyle { \int _{\left |x\right | < 1} \left | \nabla u\right |^N w_{1}(x)\,{\rm d}x = 1,}$![]() then $\displaystyle { \int _{\mathbb {R}^N} \left | \nabla u\right |^q\,{\rm d}x = 0 }$
then $\displaystyle { \int _{\mathbb {R}^N} \left | \nabla u\right |^q\,{\rm d}x = 0 }$![]() which implies that $u = 0.$
which implies that $u = 0.$![]() If $\displaystyle { \int _{\left |x\right | < 1} \left | \nabla u\right |^N w_{1}(x)\,{\rm d}x = 0,}$
If $\displaystyle { \int _{\left |x\right | < 1} \left | \nabla u\right |^N w_{1}(x)\,{\rm d}x = 0,}$![]() then $v = 0$
then $v = 0$![]() (where $v$
(where $v$![]() is given by (2.7)) and by consequence $u(x) = u(e_1),\ \forall \ x \in \mathbb {R}^N,\ 0 < \left |x\right | < 1.$
is given by (2.7)) and by consequence $u(x) = u(e_1),\ \forall \ x \in \mathbb {R}^N,\ 0 < \left |x\right | < 1.$![]() Hence, by (2.3), we get
Hence, by (2.3), we get

Thus, without loss of generality, we can assume that
Choose $\epsilon > 0$![]() such that
such that
Using again (2.3), it yields

Thus,

In view of (3.7) and (3.4), we infer

where $\widetilde {v} = (1 + \epsilon )^{\frac {1}{N'}} v.$![]() Assume that $\alpha \,{\rm e}^{\omega _{N-1}^{\frac {1}{N-1}} C_{q,N}^{N'}} \leq N.$
Assume that $\alpha \,{\rm e}^{\omega _{N-1}^{\frac {1}{N-1}} C_{q,N}^{N'}} \leq N.$![]() Taking into account that $\widetilde {v} \in W_{0,rad}^{1,N}(\mathcal {B}, \sigma _1)$
Taking into account that $\widetilde {v} \in W_{0,rad}^{1,N}(\mathcal {B}, \sigma _1)$![]() and
and
then we deduce from (1.4) that

Plainly, (1.19) immediately follows from (3.9) and (3.6).
The end of the proof of theorem 1.2 consists of showing (1.20). For that aim, we make a change of variable similar to the case $0 < \beta < 1.$![]() More precisely, for $u \in E_{q,1},$
More precisely, for $u \in E_{q,1},$![]() set $\psi (t) = \omega _{N-1}^{\frac {1}{N}} u(x)$
set $\psi (t) = \omega _{N-1}^{\frac {1}{N}} u(x)$![]() with $\left |x\right | = {\rm e}^{-t},\ t \in \mathbb {R}.$
with $\left |x\right | = {\rm e}^{-t},\ t \in \mathbb {R}.$![]() We have
We have

and

For $k \geq 0,$![]() consider the family of test functions:
consider the family of test functions:

and define $u_k \in E_{q,1}$![]() by $\psi _k(t) = \omega _{N-1}^{\frac {1}{N}} u_k(x).$
by $\psi _k(t) = \omega _{N-1}^{\frac {1}{N}} u_k(x).$![]() We have
We have
and

Observe that,

We have

which, by (3.11), leads to

Set $\widetilde {u_k}=\frac {u_k}{\left \|u_k\right \|_{E_{q,1}}}.$![]() For $\alpha > 0,$
For $\alpha > 0,$![]() we have
we have

Taking into account that

and using (3.12) we obtain that

Finally, by (3.13), we conclude that, if

then

This ends the proof of theorem 1.2.
4. Proof of theorem 1.3
We claim that

First, observe that arguing exactly as in the proof of (2.11), one can easily show that

It remains to prove that

For that aim, let $u \in E_{q,\beta }$![]() be such that $\left \|u\right \|_{q,\beta } \leq 1.$
be such that $\left \|u\right \|_{q,\beta } \leq 1.$![]() Choose $\epsilon > 0$
Choose $\epsilon > 0$![]() such that
such that

Using inequality (2.8), it follows

We have,
By the virtue of (1.2), we know that there exists a constant $C_{\beta } > 0$![]() such that
such that

On the other hand, by (2.3), we have

Putting that last inequality in (4.4), we deduce that

Since $\frac {N'}{1- \beta } \geq \frac {N' -1+ \beta }{1- \beta },$![]() then the function defined on $]1, + \infty [$
then the function defined on $]1, + \infty [$![]() by
by

is bounded. In view of (4.5), we can easily conclude that (4.3) follows. Combining (4.2) and (4.3), we deduce that (4.1) holds. Finally, if $\alpha > \alpha _{N,\beta },$![]() we proceed exactly as in the proof of theorem (1.1) keeping the same Moser sequence to prove that
we proceed exactly as in the proof of theorem (1.1) keeping the same Moser sequence to prove that

5. Proof of theorem 1.4
We claim that

First, proceeding as in the proof of (3.6), one can easily see that

Now, let $u \in E_{q,1}$![]() be such that $\left \|u\right \|_{q,1} \leq 1.$
be such that $\left \|u\right \|_{q,1} \leq 1.$![]() Without loss of generality, we can assume that
Without loss of generality, we can assume that
Using the convexity of the function defined on $[0, + \infty [$![]() by $x \longmapsto {\rm e}^{x^{N'}},$
by $x \longmapsto {\rm e}^{x^{N'}},$![]() we can easily get the following inequality
we can easily get the following inequality
For $v$![]() defined as in (2.7), it yields
defined as in (2.7), it yields
Hence,

Choose $\epsilon > 0$![]() such that
such that
Clearly, $\widetilde {v} = (1+ \epsilon ) v \in W_{0,rad}^{1,N}(\mathcal {B}, \sigma _1).$![]() We have
We have

For $\alpha \leq N,$![]() by (1.4) we get
by (1.4) we get

On the other hand, by looking at the proof of (2.3) in [Reference Su, Wang and Willem37], we can easily see that we have a more precise inequality, that is

It follows,

Hence,
Combining (5.5) and (5.4), we deduce from (5.3) that

In view of (5.6) and (5.2), we can conclude that (5.1) holds. The end of the proof gives a clear idea about the real reason of taking only the integral of $\left | \nabla u\right |^q$![]() over the set $\left \{x \in \mathbb {R}^N,\ \left |x\right | \geq 1 \right \}$
over the set $\left \{x \in \mathbb {R}^N,\ \left |x\right | \geq 1 \right \}$![]() in the definition of the norm $\left \|u\right \|_{q,1}.$
in the definition of the norm $\left \|u\right \|_{q,1}.$![]() In fact, we take the family of test functions given by (3.10) and we define as usual $u_k \in E_{q,1}$
In fact, we take the family of test functions given by (3.10) and we define as usual $u_k \in E_{q,1}$![]() by $u_k(x) = \omega _{N-1}^{-\frac {1}{N}} \psi _k(t),\ \left |x\right | = e^{-t},\ t \in \mathbb {R}.$
by $u_k(x) = \omega _{N-1}^{-\frac {1}{N}} \psi _k(t),\ \left |x\right | = e^{-t},\ t \in \mathbb {R}.$![]() Observing that $u_k(x) = 0,\ \forall \ x \in \mathbb {R}^N,\ \left |x\right | \geq 1,$
Observing that $u_k(x) = 0,\ \forall \ x \in \mathbb {R}^N,\ \left |x\right | \geq 1,$![]() we immediately get
we immediately get

Consequently, we are returning to the case of a sequence lying in $W_{0,rad}^{1,N}( \mathcal {B}, \sigma _1).$![]() Therefore, the conclusion follows.
Therefore, the conclusion follows.
6. Proof of theorem 1.5
1. Case $0 < \beta < 1:$
 Sub-case $0 < \left \|u\right \|_{E_{q,\beta }} < 1:$
Sub-case $0 < \left \|u\right \|_{E_{q,\beta }} < 1:$
Assume by contradiction that for some $0 < p_1 < (\frac {1}{1 - \left \|u\right \|_{E_{q,\beta }}^N})^{\frac {1}{(1- \beta )(N-1)}}$
 we have
(6.1)\begin{equation} \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{p_1 \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(p_1 \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x ={+} \infty. \end{equation}For $L \in ]0, + \infty [$
we have
(6.1)\begin{equation} \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{p_1 \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(p_1 \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x ={+} \infty. \end{equation}For $L \in ]0, + \infty [$
 and $v \in E_{q,\beta },$
and $v \in E_{q,\beta },$ set
(6.2)\begin{equation} G_L(v) = \left\{\begin{array}{cc} L, & \text{if}\ v > L, \\ - L, \text{if}\ v <{-}L, \\ v, & \text{if}\ \left|v\right| \leq L,\end{array} \right.\ \text{and}\ T_L(v) = v - G_L(v). \end{equation}Plainly, there exists $\epsilon > 0$
set
(6.2)\begin{equation} G_L(v) = \left\{\begin{array}{cc} L, & \text{if}\ v > L, \\ - L, \text{if}\ v <{-}L, \\ v, & \text{if}\ \left|v\right| \leq L,\end{array} \right.\ \text{and}\ T_L(v) = v - G_L(v). \end{equation}Plainly, there exists $\epsilon > 0$
 such that
\[ \left(p_1(1+ \epsilon)\right)^{(1- \beta)(N-1)} < \frac{1}{1 - \left\|u\right\|_{E_{q,\beta}}^N}. \]Since $\left \|G_L(u)\right \|_{E_{q,\beta }} \to \left \|u\right \|_{E_{q,\beta }}$
such that
\[ \left(p_1(1+ \epsilon)\right)^{(1- \beta)(N-1)} < \frac{1}{1 - \left\|u\right\|_{E_{q,\beta}}^N}. \]Since $\left \|G_L(u)\right \|_{E_{q,\beta }} \to \left \|u\right \|_{E_{q,\beta }}$
 as $L \to + \infty,$
as $L \to + \infty,$ then one can choose $L$
then one can choose $L$ large enough such that
(6.3)\begin{equation} \left(p_1(1+ \epsilon)\right)^{(1- \beta)(N-1)} < \frac{1}{1 - \left\|G_L(u)\right\|_{E_{q,\beta}}^N}. \end{equation}We claim that
large enough such that
(6.3)\begin{equation} \left(p_1(1+ \epsilon)\right)^{(1- \beta)(N-1)} < \frac{1}{1 - \left\|G_L(u)\right\|_{E_{q,\beta}}^N}. \end{equation}We claim that (6.4)\begin{align} & \limsup_{n \to + \infty} \left(\int_{\mathbb{R}^N} \left| \nabla T_L(u_n)\right|^N w_{\beta}(x)\,{\rm d}x+ \left(\int_{\mathbb{R}^N} \left| \nabla T_L(u_n)\right|^q\,{\rm d}x\right)^{\frac{N}{q}}\right)\nonumber\\ & \quad < \left( \frac{1}{p_1(1+ \epsilon)}\right)^{(1- \beta)(N-1)}. \end{align}Suppose that this does not hold. Then, there exists a subsequence of $(u_n)_n$
(6.4)\begin{align} & \limsup_{n \to + \infty} \left(\int_{\mathbb{R}^N} \left| \nabla T_L(u_n)\right|^N w_{\beta}(x)\,{\rm d}x+ \left(\int_{\mathbb{R}^N} \left| \nabla T_L(u_n)\right|^q\,{\rm d}x\right)^{\frac{N}{q}}\right)\nonumber\\ & \quad < \left( \frac{1}{p_1(1+ \epsilon)}\right)^{(1- \beta)(N-1)}. \end{align}Suppose that this does not hold. Then, there exists a subsequence of $(u_n)_n$
 that we still denote by $(u_n)_n$
that we still denote by $(u_n)_n$ such that
(6.5)\begin{align} & \int_{\mathbb{R}^N} \left| \nabla T_L(u_n) \right|^N w_{\beta}(x)\,{\rm d}x + \left(\int_{\mathbb{R}^N} \left| \nabla T_L(u_n)\right|^q\,{\rm d}x\right)^{\frac{N}{q}}\nonumber\\ & \quad \geq \left( \frac{1}{p_1(1+ \epsilon)}\right)^{(1- \beta)(N-1)},\ \forall\ n \geq 0. \end{align}Using (6.5), it yields
such that
(6.5)\begin{align} & \int_{\mathbb{R}^N} \left| \nabla T_L(u_n) \right|^N w_{\beta}(x)\,{\rm d}x + \left(\int_{\mathbb{R}^N} \left| \nabla T_L(u_n)\right|^q\,{\rm d}x\right)^{\frac{N}{q}}\nonumber\\ & \quad \geq \left( \frac{1}{p_1(1+ \epsilon)}\right)^{(1- \beta)(N-1)},\ \forall\ n \geq 0. \end{align}Using (6.5), it yields (6.6)\begin{align} 1 & = \int_{\mathbb{R}^N} \left| \nabla u_n\right|^N w_{\beta}(x)\,{\rm d}x + \left( \int_{\mathbb{R}^N} \left| \nabla u_n\right|^q\,{\rm d}x\right)^{\frac{N}{q}}\nonumber\\ & = \int_{\mathbb{R}^N} \left| \nabla T_L(u_n)\right|^N w_{\beta}(x)\,{\rm d}x + \int_{\mathbb{R}^N} \left| \nabla G_L(u_n)\right|^N w_{\beta}(x)\,{\rm d}x \nonumber\\ & \quad + \left(\int_{\mathbb{R}^N} \left| \nabla T_L(u_n)\right|^q\,{\rm d}x + \int_{\mathbb{R}^N} \left| \nabla G_L(u_n)\right|^q\,{\rm d}x\right)^{\frac{N}{q}} \nonumber\\ & \geq \int_{\mathbb{R}^N} \left| \nabla T_L(u_n)\right|^N w_{\beta}(x)\,{\rm d}x + \int_{\mathbb{R}^N} \left| \nabla G_L(u_n)\right|^N w_{\beta}(x)\,{\rm d}x \nonumber\\ & \quad + \left(\int_{\mathbb{R}^N} \left| \nabla T_L(u_n)\right|^q\,{\rm d}x\right)^{\frac{N}{q}} + \left(\int_{\mathbb{R}^N} \left| \nabla G_L(u_n)\right|^q\,{\rm d}x\right)^{\frac{N}{q}} \nonumber\\ & \geq \left( \frac{1}{p_1(1+ \epsilon)}\right)^{(1- \beta)(N-1)} + \left\|G_L(u_n)\right\|_{E_{q,\beta}}^N. \end{align}Clearly $G_L(u_n) \rightharpoonup G_L(u)$
(6.6)\begin{align} 1 & = \int_{\mathbb{R}^N} \left| \nabla u_n\right|^N w_{\beta}(x)\,{\rm d}x + \left( \int_{\mathbb{R}^N} \left| \nabla u_n\right|^q\,{\rm d}x\right)^{\frac{N}{q}}\nonumber\\ & = \int_{\mathbb{R}^N} \left| \nabla T_L(u_n)\right|^N w_{\beta}(x)\,{\rm d}x + \int_{\mathbb{R}^N} \left| \nabla G_L(u_n)\right|^N w_{\beta}(x)\,{\rm d}x \nonumber\\ & \quad + \left(\int_{\mathbb{R}^N} \left| \nabla T_L(u_n)\right|^q\,{\rm d}x + \int_{\mathbb{R}^N} \left| \nabla G_L(u_n)\right|^q\,{\rm d}x\right)^{\frac{N}{q}} \nonumber\\ & \geq \int_{\mathbb{R}^N} \left| \nabla T_L(u_n)\right|^N w_{\beta}(x)\,{\rm d}x + \int_{\mathbb{R}^N} \left| \nabla G_L(u_n)\right|^N w_{\beta}(x)\,{\rm d}x \nonumber\\ & \quad + \left(\int_{\mathbb{R}^N} \left| \nabla T_L(u_n)\right|^q\,{\rm d}x\right)^{\frac{N}{q}} + \left(\int_{\mathbb{R}^N} \left| \nabla G_L(u_n)\right|^q\,{\rm d}x\right)^{\frac{N}{q}} \nonumber\\ & \geq \left( \frac{1}{p_1(1+ \epsilon)}\right)^{(1- \beta)(N-1)} + \left\|G_L(u_n)\right\|_{E_{q,\beta}}^N. \end{align}Clearly $G_L(u_n) \rightharpoonup G_L(u)$
 weakly in $E_{q,\beta }.$
weakly in $E_{q,\beta }.$ Consequently, passing to the lower limit as $n$
Consequently, passing to the lower limit as $n$ tends to $+ \infty$
tends to $+ \infty$ in (6.6), we obtain
\[ 1 \geq \left\|G_L(u)\right\|_{E_{q,\beta}}^N + \left( \frac{1}{p_1(1+ \epsilon)}\right)^{(1- \beta)(N-1)}. \]Thus,
in (6.6), we obtain
\[ 1 \geq \left\|G_L(u)\right\|_{E_{q,\beta}}^N + \left( \frac{1}{p_1(1+ \epsilon)}\right)^{(1- \beta)(N-1)}. \]Thus, \[ \left( p_1(1+ \epsilon)\right)^{(1- \beta)(N-1)} \geq \frac{1}{1- \left\|G_L(u)\right\|_{E_{q,\beta}}^N}, \]which is in contradiction with (6.3). Therefore, our claim (6.4) is true. Set
\[ \left( p_1(1+ \epsilon)\right)^{(1- \beta)(N-1)} \geq \frac{1}{1- \left\|G_L(u)\right\|_{E_{q,\beta}}^N}, \]which is in contradiction with (6.3). Therefore, our claim (6.4) is true. Set \[ \Omega_{n,L} = \left\{x \in \mathbb{R}^N,\ \left|u_n(x)\right| \geq L\right\}. \]By (6.4), up to a subsequence,
\[ \Omega_{n,L} = \left\{x \in \mathbb{R}^N,\ \left|u_n(x)\right| \geq L\right\}. \]By (6.4), up to a subsequence, \[ \left\|\left(p_1(1+ \epsilon)\right)^{\frac{(1- \beta)}{N'}} T_L(u_n)\right\|_{ E_{q,\beta}} < 1,\ \forall\ n \geq 0. \]We have
\[ \left\|\left(p_1(1+ \epsilon)\right)^{\frac{(1- \beta)}{N'}} T_L(u_n)\right\|_{ E_{q,\beta}} < 1,\ \forall\ n \geq 0. \]We have (6.7)\begin{align} & \int_{\Omega_{n,L}} \left({\rm e}^{\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right)\,{\rm d}x\nonumber\\ & = \int_{\Omega_{n,L} \cap \mathcal{B}} \left({\rm e}^{\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right)\,{\rm d}x \nonumber\\ & \quad + \int_{\Omega_{n,L} \cap \mathcal{B}^c} \left({\rm e}^{\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right)\,{\rm d}x. \end{align}On the one hand, by (2.8), we get
(6.7)\begin{align} & \int_{\Omega_{n,L}} \left({\rm e}^{\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right)\,{\rm d}x\nonumber\\ & = \int_{\Omega_{n,L} \cap \mathcal{B}} \left({\rm e}^{\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right)\,{\rm d}x \nonumber\\ & \quad + \int_{\Omega_{n,L} \cap \mathcal{B}^c} \left({\rm e}^{\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right)\,{\rm d}x. \end{align}On the one hand, by (2.8), we get (6.8)\begin{align} & \int_{\Omega_{n,L} \cap \mathcal{B}} \left({\rm e}^{\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x \nonumber\\ & \leq \int_{\Omega_{n,L} \cap \mathcal{B}}\,{\rm e}^{\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}}\,{\rm d}x \nonumber\\ & \leq \int_{\Omega_{n,L} \cap \mathcal{B}}\,{\rm e}^{p_1 \alpha_{N,\beta} (1+ \epsilon) \left|u_n -L\right|^{\frac{N'}{1- \beta}}}\,{\rm e}^{p_1 \alpha_{N,\beta} A(\epsilon) L^{\frac{N'}{1- \beta}}}\,{\rm d}x \nonumber\\ & \leq {\rm e}^{p_1 \alpha_{N,\beta} A(\epsilon) L^{\frac{N'}{1- \beta}}} \int_{\Omega_{n,L} \cap \mathcal{B}}\,{\rm e}^{p_1 \alpha_{N,\beta} (1+ \epsilon) \left|T_L(u_n)\right|^{\frac{N'}{1- \beta}}}\,{\rm d}x \nonumber\\ & \leq {\rm e}^{p_1 \alpha_{N,\beta} A(\epsilon) L^{\frac{N'}{1- \beta}}} \int_{\mathcal{B}}\,{\rm e}^{p_1 \alpha_{N,\beta} (1+ \epsilon) \left|T_L(u_n)\right|^{\frac{N'}{1- \beta}}}\,{\rm d}x, \end{align}where $A(\epsilon ) = \frac {1+\epsilon }{((1+\epsilon )^{\frac {1-\beta }{N'-1+\beta }}-1)^{\frac {N'-1+\beta }{1-\beta }}}.$
(6.8)\begin{align} & \int_{\Omega_{n,L} \cap \mathcal{B}} \left({\rm e}^{\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x \nonumber\\ & \leq \int_{\Omega_{n,L} \cap \mathcal{B}}\,{\rm e}^{\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}}\,{\rm d}x \nonumber\\ & \leq \int_{\Omega_{n,L} \cap \mathcal{B}}\,{\rm e}^{p_1 \alpha_{N,\beta} (1+ \epsilon) \left|u_n -L\right|^{\frac{N'}{1- \beta}}}\,{\rm e}^{p_1 \alpha_{N,\beta} A(\epsilon) L^{\frac{N'}{1- \beta}}}\,{\rm d}x \nonumber\\ & \leq {\rm e}^{p_1 \alpha_{N,\beta} A(\epsilon) L^{\frac{N'}{1- \beta}}} \int_{\Omega_{n,L} \cap \mathcal{B}}\,{\rm e}^{p_1 \alpha_{N,\beta} (1+ \epsilon) \left|T_L(u_n)\right|^{\frac{N'}{1- \beta}}}\,{\rm d}x \nonumber\\ & \leq {\rm e}^{p_1 \alpha_{N,\beta} A(\epsilon) L^{\frac{N'}{1- \beta}}} \int_{\mathcal{B}}\,{\rm e}^{p_1 \alpha_{N,\beta} (1+ \epsilon) \left|T_L(u_n)\right|^{\frac{N'}{1- \beta}}}\,{\rm d}x, \end{align}where $A(\epsilon ) = \frac {1+\epsilon }{((1+\epsilon )^{\frac {1-\beta }{N'-1+\beta }}-1)^{\frac {N'-1+\beta }{1-\beta }}}.$
 Having in mind that $\left |u_n(x)\right | = \left |u_n(e_1)\right | \leq C_{q,N},\ \forall \ x \in \mathbb {R}^N,\ \left |x\right | = 1,$
Having in mind that $\left |u_n(x)\right | = \left |u_n(e_1)\right | \leq C_{q,N},\ \forall \ x \in \mathbb {R}^N,\ \left |x\right | = 1,$ then
\[ T_L(u_n(x)) = 0,\ \forall\ x \in \mathbb{R}^N,\ \left|x\right| = 1,\ \forall\ L > C_{q,N}. \]Consequently, $T_L(u_n) \in W_{0,rad}^{1,N}( \mathcal {B}, \sigma _{\beta }),\ \forall \ L > C_{q,N}.$
then
\[ T_L(u_n(x)) = 0,\ \forall\ x \in \mathbb{R}^N,\ \left|x\right| = 1,\ \forall\ L > C_{q,N}. \]Consequently, $T_L(u_n) \in W_{0,rad}^{1,N}( \mathcal {B}, \sigma _{\beta }),\ \forall \ L > C_{q,N}.$
 Since
\[ \int_{\mathcal{B}} \left| \nabla (p_1(1+ \epsilon))^{\frac{1- \beta}{N'}}T_L(u_n)\right|^N w_{\beta}(x)\,{\rm d}x < 1, \]then by (1.2), we infer
Since
\[ \int_{\mathcal{B}} \left| \nabla (p_1(1+ \epsilon))^{\frac{1- \beta}{N'}}T_L(u_n)\right|^N w_{\beta}(x)\,{\rm d}x < 1, \]then by (1.2), we infer \[ \sup_{n} \int_{\mathcal{B}}\,{\rm e}^{p_1 \alpha_{N,\beta} (1+ \epsilon) \left|T_L(u_n)\right|^{\frac{N'}{1- \beta}}}\,{\rm d}x <{+} \infty,\ \forall\ L > C_{q,N}. \]Putting that result in (6.8), we obtain
\[ \sup_{n} \int_{\mathcal{B}}\,{\rm e}^{p_1 \alpha_{N,\beta} (1+ \epsilon) \left|T_L(u_n)\right|^{\frac{N'}{1- \beta}}}\,{\rm d}x <{+} \infty,\ \forall\ L > C_{q,N}. \]Putting that result in (6.8), we obtain (6.9)\begin{align} & \sup_n \int_{\Omega_{n,L} \cap \mathcal{B}} \left({\rm e}^{\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x \nonumber\\ & \quad <{+} \infty,\ \forall\ L > C_{q,N}. \end{align}On the other hand, in view of (2.3), we know that
(6.9)\begin{align} & \sup_n \int_{\Omega_{n,L} \cap \mathcal{B}} \left({\rm e}^{\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x \nonumber\\ & \quad <{+} \infty,\ \forall\ L > C_{q,N}. \end{align}On the other hand, in view of (2.3), we know that \[ \left|u_n(x)\right| \leq C_{q,N} \left| \nabla u_n\right|_{L^q(\mathbb{R}^N)} \leq C_{q,N},\ \forall\ x \in \mathbb{R}^N,\ \left|x\right| \geq 1. \]Hence,
\[ \left|u_n(x)\right| \leq C_{q,N} \left| \nabla u_n\right|_{L^q(\mathbb{R}^N)} \leq C_{q,N},\ \forall\ x \in \mathbb{R}^N,\ \left|x\right| \geq 1. \]Hence, \[ \Omega_{n,L}\cap \mathcal{B}^c = \emptyset,\ \forall\ L > C_{q,N}. \]We deduce from (6.9) and (6.7) that
\[ \Omega_{n,L}\cap \mathcal{B}^c = \emptyset,\ \forall\ L > C_{q,N}. \]We deduce from (6.9) and (6.7) that (6.10)\begin{equation} \sup_n \int_{\Omega_{n,L}} \left({\rm e}^{\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}} \!-\!S_{j_{\beta}-1}\left(\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x \!<\!{+}\infty,\ \forall\ L \!>\! C_{q,N}. \end{equation}Next, observe that
(6.10)\begin{equation} \sup_n \int_{\Omega_{n,L}} \left({\rm e}^{\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}} \!-\!S_{j_{\beta}-1}\left(\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x \!<\!{+}\infty,\ \forall\ L \!>\! C_{q,N}. \end{equation}Next, observe that \begin{align*} & \int_{\Omega_{n,L}^c} \left({\rm e}^{p_1 \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x \\ & = \int_{\left|u_n\right| < L} \sum_{j=j_{\beta}}^{+ \infty} \frac{(p_1 \alpha_{N,\beta})^j}{j!} \left|u_n\right|^{\frac{jN'}{1- \beta}}\,{\rm d}x \\ & = \int_{\left|u_n\right| < L} \sum_{j=j_{\beta}}^{+ \infty} \frac{(p_1 \alpha_{N,\beta})^j}{j!} \left|\frac{u_n}{L}\right|^{\frac{jN'}{1- \beta}} L^{\frac{jN'}{1- \beta}}\,{\rm d}x \\ & \leq c_4 \sum_{j=j_{\beta}}^{+ \infty} \frac{(p_1 \alpha_{N, \beta} L^{\frac{N'}{1- \beta}})^j}{j!} \int_{\left|u_n\right| < L}\left|\frac{u_n}{L}\right|^{j_{\beta}\frac{N'}{1- \beta}}\,{\rm d}x \\ & \leq c_4 \sum_{j=j_{\beta}}^{+ \infty} \frac{(p_1 \alpha_{N, \beta} L^{\frac{N'}{1- \beta}})^j}{j!} \int_{\left|u_n\right| < L} \left|\frac{u_n}{L}\right|^{q^{*}}\,{\rm d}x \\ & \leq c_4 \frac{{\rm e}^{p_1 \alpha_{N, \beta} L^{\frac{N'}{1- \beta}}}}{L^{q^*}} \int_{\mathbb{R}^N} \left|u_n\right|^{q^*}\,{\rm d}x \\ & \leq c_5 \frac{{\rm e}^{p_1 \alpha_{N, \beta} L^{\frac{N'}{1- \beta}}}}{L^{q^*}}, \end{align*}where we used the fact that $j_{\beta } \geq \frac {(1- \beta )q^*}{N'}$
\begin{align*} & \int_{\Omega_{n,L}^c} \left({\rm e}^{p_1 \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x \\ & = \int_{\left|u_n\right| < L} \sum_{j=j_{\beta}}^{+ \infty} \frac{(p_1 \alpha_{N,\beta})^j}{j!} \left|u_n\right|^{\frac{jN'}{1- \beta}}\,{\rm d}x \\ & = \int_{\left|u_n\right| < L} \sum_{j=j_{\beta}}^{+ \infty} \frac{(p_1 \alpha_{N,\beta})^j}{j!} \left|\frac{u_n}{L}\right|^{\frac{jN'}{1- \beta}} L^{\frac{jN'}{1- \beta}}\,{\rm d}x \\ & \leq c_4 \sum_{j=j_{\beta}}^{+ \infty} \frac{(p_1 \alpha_{N, \beta} L^{\frac{N'}{1- \beta}})^j}{j!} \int_{\left|u_n\right| < L}\left|\frac{u_n}{L}\right|^{j_{\beta}\frac{N'}{1- \beta}}\,{\rm d}x \\ & \leq c_4 \sum_{j=j_{\beta}}^{+ \infty} \frac{(p_1 \alpha_{N, \beta} L^{\frac{N'}{1- \beta}})^j}{j!} \int_{\left|u_n\right| < L} \left|\frac{u_n}{L}\right|^{q^{*}}\,{\rm d}x \\ & \leq c_4 \frac{{\rm e}^{p_1 \alpha_{N, \beta} L^{\frac{N'}{1- \beta}}}}{L^{q^*}} \int_{\mathbb{R}^N} \left|u_n\right|^{q^*}\,{\rm d}x \\ & \leq c_5 \frac{{\rm e}^{p_1 \alpha_{N, \beta} L^{\frac{N'}{1- \beta}}}}{L^{q^*}}, \end{align*}where we used the fact that $j_{\beta } \geq \frac {(1- \beta )q^*}{N'}$
 together with the boundedness of the sequence $(u_n)_n$
together with the boundedness of the sequence $(u_n)_n$ in $L^{q^*}( \mathbb {R}^N).$
in $L^{q^*}( \mathbb {R}^N).$ Therefore,
(6.11)\begin{equation} \sup_{n} \int_{\Omega_{n,L}^c} \left(e^{p_1 \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x <{+} \infty. \end{equation}Combining (6.11) and (6.10), we conclude that
Therefore,
(6.11)\begin{equation} \sup_{n} \int_{\Omega_{n,L}^c} \left(e^{p_1 \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x <{+} \infty. \end{equation}Combining (6.11) and (6.10), we conclude that \[ \sup_{n} \int_{\mathbb{R}^N} \left({\rm e}^{p_1 \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x <{+} \infty, \]which, in view of (6.1), leads to the expected contradiction. Case $\left \|u\right \|_{E_{q,\beta }} = 1:$
\[ \sup_{n} \int_{\mathbb{R}^N} \left({\rm e}^{p_1 \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p_1 \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x <{+} \infty, \]which, in view of (6.1), leads to the expected contradiction. Case $\left \|u\right \|_{E_{q,\beta }} = 1:$
 Since $u_n \rightharpoonup u$
Since $u_n \rightharpoonup u$ weakly in $E_{q,\beta }$
weakly in $E_{q,\beta }$ which is uniformly convex, then $u_n \to u$
which is uniformly convex, then $u_n \to u$ strongly in $E_{q,\beta }$
strongly in $E_{q,\beta }$ (see [Reference Brezis12, proposition 3.32]). We can easily adapt the arguments used in the proof of [Reference do Ó, Medeiros and Severo23, proposition1] to deduce that there exists $v \in E_{q,\beta }$
(see [Reference Brezis12, proposition 3.32]). We can easily adapt the arguments used in the proof of [Reference do Ó, Medeiros and Severo23, proposition1] to deduce that there exists $v \in E_{q,\beta }$ such that, up to a subsequence, $\left |u_n(x)\right | \leq v(x)$
such that, up to a subsequence, $\left |u_n(x)\right | \leq v(x)$ a.e. $x \in \mathbb {R}^N,\ \forall \ n.$
a.e. $x \in \mathbb {R}^N,\ \forall \ n.$ Let $0 < p < + \infty.$
Let $0 < p < + \infty.$ We have
\begin{align*} & \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{p \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(p \alpha_{N, \beta} \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x \\ & = \sup_n \sum_{j= j_{\beta}}^{+ \infty} \int_{\mathbb{R}^N} \frac{(p \alpha_{N,\beta}\left|u_n \right|^{\frac{N'}{1- \beta}})^j}{j!}\,{\rm d}x \\ & \leq \sum_{j= j_{\beta}}^{+ \infty} \int_{\mathbb{R}^N} \frac{(p \alpha_{N,\beta}\left|v \right|^{\frac{N'}{1- \beta}})^j}{j!}\,{\rm d}x \\ & = \int_{\mathbb{R}^N} \left({\rm e}^{p \alpha_{N, \beta} \left|v\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(p \alpha_{N, \beta} \left|v\right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x <{+} \infty. \end{align*}
We have
\begin{align*} & \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{p \alpha_{N, \beta} \left|u_n\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(p \alpha_{N, \beta} \left|u_n \right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x \\ & = \sup_n \sum_{j= j_{\beta}}^{+ \infty} \int_{\mathbb{R}^N} \frac{(p \alpha_{N,\beta}\left|u_n \right|^{\frac{N'}{1- \beta}})^j}{j!}\,{\rm d}x \\ & \leq \sum_{j= j_{\beta}}^{+ \infty} \int_{\mathbb{R}^N} \frac{(p \alpha_{N,\beta}\left|v \right|^{\frac{N'}{1- \beta}})^j}{j!}\,{\rm d}x \\ & = \int_{\mathbb{R}^N} \left({\rm e}^{p \alpha_{N, \beta} \left|v\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(p \alpha_{N, \beta} \left|v\right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x <{+} \infty. \end{align*}
Now, we exhibit a sequence $(\xi _k)_k \subset E_{q,\beta }$
 and a function $\xi \in E_{q,\beta }{\setminus} {\left \{0\right \}}$
and a function $\xi \in E_{q,\beta }{\setminus} {\left \{0\right \}}$ such that $\left \|\xi _k\right \|_{E_{q,\beta }} = 1,\ \xi _k \rightharpoonup \xi$
such that $\left \|\xi _k\right \|_{E_{q,\beta }} = 1,\ \xi _k \rightharpoonup \xi$ weakly in $E_{q,\beta },\ \left \|\xi \right \|_{E_{q,\beta }} < 1,$
weakly in $E_{q,\beta },\ \left \|\xi \right \|_{E_{q,\beta }} < 1,$ and
\begin{align*} & \int_{\mathbb{R}^N} \left({\rm e}^{\alpha_{N, \beta} p \left|\xi_k\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left( \alpha_{N, \beta} p \left|\xi_k\right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x\\ & \quad \to + \infty,\ k \to + \infty,\ \forall\ p > P_{N,\beta}(\xi). \end{align*}For $k \in \mathbb {N}\backslash {\left \{0\right \}}$
and
\begin{align*} & \int_{\mathbb{R}^N} \left({\rm e}^{\alpha_{N, \beta} p \left|\xi_k\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left( \alpha_{N, \beta} p \left|\xi_k\right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x\\ & \quad \to + \infty,\ k \to + \infty,\ \forall\ p > P_{N,\beta}(\xi). \end{align*}For $k \in \mathbb {N}\backslash {\left \{0\right \}}$
 and $\lambda \in ]0, + \infty [$
and $\lambda \in ]0, + \infty [$ to be fixed later, we define the function $\psi _k:\mathbb {R} \to \mathbb {R}$
to be fixed later, we define the function $\psi _k:\mathbb {R} \to \mathbb {R}$ by
\[ \psi_k(t) = \lambda \left\{\begin{array}{ll} \dfrac{t^{1- \beta} - (1/2)^{1- \beta}}{\left(k^{1- \beta} - (1/2)^{1- \beta}\right)^{\dfrac{1}{N}}}, & 1/2 \leq t \leq k, \\ \left(k^{1- \beta} - (1/2)^{1- \beta}\right)^{\dfrac{1}{N'}}, & t \geq k, \\ 0, & t \leq 1/2. \end{array} \right. \]We also define the function $\psi :[0, + \infty [ \to [0, + \infty [$
by
\[ \psi_k(t) = \lambda \left\{\begin{array}{ll} \dfrac{t^{1- \beta} - (1/2)^{1- \beta}}{\left(k^{1- \beta} - (1/2)^{1- \beta}\right)^{\dfrac{1}{N}}}, & 1/2 \leq t \leq k, \\ \left(k^{1- \beta} - (1/2)^{1- \beta}\right)^{\dfrac{1}{N'}}, & t \geq k, \\ 0, & t \leq 1/2. \end{array} \right. \]We also define the function $\psi :[0, + \infty [ \to [0, + \infty [$
 by
\[ \psi(t) = a \left\{\begin{array}{ll} 0, & t \leq 1/4, \\ \dfrac{t^{1- \beta} - (1/4)^{1- \beta}}{\left((1/2)^{1- \beta} - (1/4)^{1- \beta}\right)^{\dfrac{1}{N}}}, & 1/4 \leq t \leq 1/2, \\ \left((1/2)^{1- \beta} - (1/4)^{1- \beta}\right)^{\dfrac{1}{N'}}, & t \geq 1/2, \end{array} \right. \]where $a > 0.$
by
\[ \psi(t) = a \left\{\begin{array}{ll} 0, & t \leq 1/4, \\ \dfrac{t^{1- \beta} - (1/4)^{1- \beta}}{\left((1/2)^{1- \beta} - (1/4)^{1- \beta}\right)^{\dfrac{1}{N}}}, & 1/4 \leq t \leq 1/2, \\ \left((1/2)^{1- \beta} - (1/4)^{1- \beta}\right)^{\dfrac{1}{N'}}, & t \geq 1/2, \end{array} \right. \]where $a > 0.$
 Set $u_k(x) = \omega _{N-1}^{-\frac {1}{N}} \psi _k(t),\ u(x) = \omega _{N-1}^{-\frac {1}{N}} \psi (t),\ \left |x\right | = {\rm e}^{-t},\ t \in \mathbb {R}.$
Set $u_k(x) = \omega _{N-1}^{-\frac {1}{N}} \psi _k(t),\ u(x) = \omega _{N-1}^{-\frac {1}{N}} \psi (t),\ \left |x\right | = {\rm e}^{-t},\ t \in \mathbb {R}.$ We have
\begin{align*} \int_{\mathbb{R}^N} \left| \nabla u_k\right|^N w_{\beta}(x)\,{\rm d}x & = \int_{0}^{+ \infty} t^{\beta(N-1)} \left|\psi_k'(t)\right|^{N}\,{\rm d}t\\ & = \lambda^N \int_{1/2}^k \frac{t^{\beta(N-1)} (1- \beta)^N t^{- \beta N}}{k^{1- \beta} - (1/2)^{1- \beta}}\,{\rm d}t \\ & = \lambda^N (1- \beta)^{N-1}. \end{align*}Furthermore,
We have
\begin{align*} \int_{\mathbb{R}^N} \left| \nabla u_k\right|^N w_{\beta}(x)\,{\rm d}x & = \int_{0}^{+ \infty} t^{\beta(N-1)} \left|\psi_k'(t)\right|^{N}\,{\rm d}t\\ & = \lambda^N \int_{1/2}^k \frac{t^{\beta(N-1)} (1- \beta)^N t^{- \beta N}}{k^{1- \beta} - (1/2)^{1- \beta}}\,{\rm d}t \\ & = \lambda^N (1- \beta)^{N-1}. \end{align*}Furthermore, \begin{align*} \int_{\mathbb{R}^N} \left| \nabla u_k\right|^q\,{\rm d}x & = \omega_{N-1}^{1- \frac{q}{N}} \int_{1/2}^k \left|\psi_k'(t)\right|^q\,{\rm e}^{(q-N)t}\,{\rm d}t\\ & = \frac{ \lambda^q\omega_{N-1}^{1- \frac{q}{N}} (1- \beta)^q}{\left(k^{1- \beta} - (1/2)^{1- \beta}\right)^{\frac{q}{N}}} \int_{1/2}^k \frac{{\rm e}^{(q-N)t}}{t^{q \beta}}\,{\rm d}t. \end{align*}Clearly,
\begin{align*} \int_{\mathbb{R}^N} \left| \nabla u_k\right|^q\,{\rm d}x & = \omega_{N-1}^{1- \frac{q}{N}} \int_{1/2}^k \left|\psi_k'(t)\right|^q\,{\rm e}^{(q-N)t}\,{\rm d}t\\ & = \frac{ \lambda^q\omega_{N-1}^{1- \frac{q}{N}} (1- \beta)^q}{\left(k^{1- \beta} - (1/2)^{1- \beta}\right)^{\frac{q}{N}}} \int_{1/2}^k \frac{{\rm e}^{(q-N)t}}{t^{q \beta}}\,{\rm d}t. \end{align*}Clearly, \[ \int_{\mathbb{R}^N} \left| \nabla u_k\right|^q\,{\rm d}x \to 0,\ k \to + \infty. \]Set $v_k = u + u_k.$
\[ \int_{\mathbb{R}^N} \left| \nabla u_k\right|^q\,{\rm d}x \to 0,\ k \to + \infty. \]Set $v_k = u + u_k.$
 It yields,
\begin{align*} \left\|v_k\right\|_{E_{q,\beta}}^N & = \int_{\mathbb{R}^N} \left| \nabla u_k\right|^N w_{\beta}(x)\,{\rm d}x + \int_{\mathbb{R}^N} \left| \nabla u\right|^N w_{\beta}(x)\, {\rm d}x\\ & \quad + \left( \int_{\mathbb{R}^N} \left| \nabla u_k\right|^q\,{\rm d}x + \int_{\mathbb{R}^N} \left| \nabla u\right|^q\,{\rm d}x\right)^{\frac{N}{q}} \\ & = (1- \beta)^{N-1}(a^N + \lambda^N) + \left( \int_{\mathbb{R}^N} \left| \nabla u_k\right|^q\,{\rm d}x + \int_{\mathbb{R}^N} \left| \nabla u\right|^q\,{\rm d}x\right)^{\frac{N}{q}}. \end{align*}Consequently,
It yields,
\begin{align*} \left\|v_k\right\|_{E_{q,\beta}}^N & = \int_{\mathbb{R}^N} \left| \nabla u_k\right|^N w_{\beta}(x)\,{\rm d}x + \int_{\mathbb{R}^N} \left| \nabla u\right|^N w_{\beta}(x)\, {\rm d}x\\ & \quad + \left( \int_{\mathbb{R}^N} \left| \nabla u_k\right|^q\,{\rm d}x + \int_{\mathbb{R}^N} \left| \nabla u\right|^q\,{\rm d}x\right)^{\frac{N}{q}} \\ & = (1- \beta)^{N-1}(a^N + \lambda^N) + \left( \int_{\mathbb{R}^N} \left| \nabla u_k\right|^q\,{\rm d}x + \int_{\mathbb{R}^N} \left| \nabla u\right|^q\,{\rm d}x\right)^{\frac{N}{q}}. \end{align*}Consequently, \begin{align*} & \left\|v_k\right\|_{E_{q,\beta}}^N \to (1- \beta)^{N-1}(a^N + \lambda^N) + \left(\int_{\mathbb{R}^N} \left| \nabla u\right|^q\,{\rm d}x\right)^{\frac{N}{q}}\\ & \quad = (1- \beta)^{N-1} \lambda^N + \left\|u\right\|_{E_{q,\beta}}^N,\ k \to + \infty, \end{align*}where we used the fact that
\begin{align*} & \left\|v_k\right\|_{E_{q,\beta}}^N \to (1- \beta)^{N-1}(a^N + \lambda^N) + \left(\int_{\mathbb{R}^N} \left| \nabla u\right|^q\,{\rm d}x\right)^{\frac{N}{q}}\\ & \quad = (1- \beta)^{N-1} \lambda^N + \left\|u\right\|_{E_{q,\beta}}^N,\ k \to + \infty, \end{align*}where we used the fact that \begin{align*} & \left\|u\right\|_{E_{q,\beta}}^N = \int_{\mathbb{R}^N} \left| \nabla u\right|^N w_{\beta}(x)\,{\rm d}x + \left(\int_{\mathbb{R}^N} \left| \nabla u\right|^q\,{\rm d}x\right)^{\frac{N}{q}}\\ & \quad = (1- \beta)^{N-1} a^N + \left(\int_{\mathbb{R}^N} \left| \nabla u\right|^q\,{\rm d}x\right)^{\frac{N}{q}}. \end{align*}Choose $\lambda > 0$
\begin{align*} & \left\|u\right\|_{E_{q,\beta}}^N = \int_{\mathbb{R}^N} \left| \nabla u\right|^N w_{\beta}(x)\,{\rm d}x + \left(\int_{\mathbb{R}^N} \left| \nabla u\right|^q\,{\rm d}x\right)^{\frac{N}{q}}\\ & \quad = (1- \beta)^{N-1} a^N + \left(\int_{\mathbb{R}^N} \left| \nabla u\right|^q\,{\rm d}x\right)^{\frac{N}{q}}. \end{align*}Choose $\lambda > 0$
 and $a > 0$
and $a > 0$ such that
(6.12)\begin{equation} (1- \beta)^{N-1} \lambda^N + \left\|u\right\|_{E_{q,\beta}}^N = 1. \end{equation}One can easily see that $u_k \rightharpoonup 0$
such that
(6.12)\begin{equation} (1- \beta)^{N-1} \lambda^N + \left\|u\right\|_{E_{q,\beta}}^N = 1. \end{equation}One can easily see that $u_k \rightharpoonup 0$
 weakly in $E_{q, \beta }.$
weakly in $E_{q, \beta }.$ By (6.12), we derive that $\frac {v_k}{ \left \|v_k\right \|_{E_{q,\beta }}}\rightharpoonup u$
By (6.12), we derive that $\frac {v_k}{ \left \|v_k\right \|_{E_{q,\beta }}}\rightharpoonup u$ weakly in $E_{q,\beta }.$
weakly in $E_{q,\beta }.$ Let $p > P_{N,\beta }(u).$
Let $p > P_{N,\beta }(u).$ Then, there exists $\epsilon > 0$
Then, there exists $\epsilon > 0$ such that $p = (1+ \epsilon ) P_{N,\beta }(u).$
such that $p = (1+ \epsilon ) P_{N,\beta }(u).$ We have
(6.13)\begin{align} & \int_{\mathbb{R}^N} \left({\rm e}^{\alpha_{N, \beta} p \left| \frac{v_k}{\left\|v_k\right\|_{E_{q,\beta}}}\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p \left| \frac{v_k}{\left\|v_k\right\|_{E_{q,\beta}}}\right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x \nonumber\\ & \geq \omega_{N-1} \int_k^{+ \infty} \exp\left(\frac{\alpha_{N, \beta} p \omega_{N-1}^{- \frac{1}{(N-1)(1- \beta)}} \left| \psi(t) + \psi_k(t)\right|^{\frac{N'}{1- \beta}}}{\left\|v_k\right\|_{E_{q,\beta}}^{\frac{N'}{1- \beta}}}\right) {\rm e}^{{-}Nt}\,{\rm d}t \nonumber\\ & \quad - \sum_{j=0}^{j_{\beta}-1} \frac{( \alpha_{N,\beta} p)^{j}}{j!} \frac{1}{\left\|v_k\right\|_{E_{q\beta}}^{\frac{jN'}{1- \beta}}} \int_{\mathbb{R}^N} \left|v_k\right|^{\frac{jN'}{1- \beta}}\,{\rm d}x \nonumber\\ & = \omega_{N-1} \frac{{\rm e}^{{-}Nk}}{N} \exp\left(\vphantom{\left.\left.\quad + \lambda \left(k^{1- \beta} - (1/2)^{1- \beta}\right)^{\frac{1}{N'}}\right)^{\frac{N'}{1- \beta}}\right)}\theta_k\left(a\left((1/2)^{1- \beta} - (1/4)^{1- \beta}\right)^{\frac{1}{N'}}\right.\right.\nonumber\\ & \left.\left.\quad + \lambda \left(k^{1- \beta} - (1/2)^{1- \beta}\right)^{\frac{1}{N'}}\right)^{\frac{N'}{1- \beta}}\right) \nonumber\\ & \quad -\sum_{j=0}^{j_{\beta}-1} \frac{( \alpha_{N,\beta} p)^{j}}{j!} \frac{1}{\left\|v_k\right\|_{E_{q,\beta}}^{\frac{jN'}{1- \beta}}} \int_{\mathbb{R}^N} \left|v_k\right|^{\frac{jN'}{1- \beta}}\,{\rm d}x, \end{align}where
We have
(6.13)\begin{align} & \int_{\mathbb{R}^N} \left({\rm e}^{\alpha_{N, \beta} p \left| \frac{v_k}{\left\|v_k\right\|_{E_{q,\beta}}}\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p \left| \frac{v_k}{\left\|v_k\right\|_{E_{q,\beta}}}\right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x \nonumber\\ & \geq \omega_{N-1} \int_k^{+ \infty} \exp\left(\frac{\alpha_{N, \beta} p \omega_{N-1}^{- \frac{1}{(N-1)(1- \beta)}} \left| \psi(t) + \psi_k(t)\right|^{\frac{N'}{1- \beta}}}{\left\|v_k\right\|_{E_{q,\beta}}^{\frac{N'}{1- \beta}}}\right) {\rm e}^{{-}Nt}\,{\rm d}t \nonumber\\ & \quad - \sum_{j=0}^{j_{\beta}-1} \frac{( \alpha_{N,\beta} p)^{j}}{j!} \frac{1}{\left\|v_k\right\|_{E_{q\beta}}^{\frac{jN'}{1- \beta}}} \int_{\mathbb{R}^N} \left|v_k\right|^{\frac{jN'}{1- \beta}}\,{\rm d}x \nonumber\\ & = \omega_{N-1} \frac{{\rm e}^{{-}Nk}}{N} \exp\left(\vphantom{\left.\left.\quad + \lambda \left(k^{1- \beta} - (1/2)^{1- \beta}\right)^{\frac{1}{N'}}\right)^{\frac{N'}{1- \beta}}\right)}\theta_k\left(a\left((1/2)^{1- \beta} - (1/4)^{1- \beta}\right)^{\frac{1}{N'}}\right.\right.\nonumber\\ & \left.\left.\quad + \lambda \left(k^{1- \beta} - (1/2)^{1- \beta}\right)^{\frac{1}{N'}}\right)^{\frac{N'}{1- \beta}}\right) \nonumber\\ & \quad -\sum_{j=0}^{j_{\beta}-1} \frac{( \alpha_{N,\beta} p)^{j}}{j!} \frac{1}{\left\|v_k\right\|_{E_{q,\beta}}^{\frac{jN'}{1- \beta}}} \int_{\mathbb{R}^N} \left|v_k\right|^{\frac{jN'}{1- \beta}}\,{\rm d}x, \end{align}where \begin{align*} \theta_k & = \frac{\alpha_{N, \beta} p \omega_{N-1}^{- \frac{1}{(N-1)(1- \beta)}}}{\left\|v_k\right\|_{E_{q,\beta}}^{\frac{N'}{1- \beta}}} \to N (1- \beta)^{\frac{1}{1- \beta}} p\\ & = N (1- \beta)^{\frac{1}{1- \beta}} (1+\epsilon) P_{N,\beta}(u),\ k \to + \infty. \end{align*}On the other hand, by (6.12), we have
\begin{align*} \theta_k & = \frac{\alpha_{N, \beta} p \omega_{N-1}^{- \frac{1}{(N-1)(1- \beta)}}}{\left\|v_k\right\|_{E_{q,\beta}}^{\frac{N'}{1- \beta}}} \to N (1- \beta)^{\frac{1}{1- \beta}} p\\ & = N (1- \beta)^{\frac{1}{1- \beta}} (1+\epsilon) P_{N,\beta}(u),\ k \to + \infty. \end{align*}On the other hand, by (6.12), we have \begin{align*} P_{N,\beta}(u) & = \frac{1}{\left(1- \left\|u\right\|_{E_{q,\beta}}^N\right)^{\frac{1}{(N-1)(1- \beta)}}} = \frac{1}{\left((1- \beta)^{N-1} \lambda^N\right)^{\frac{1}{(N-1)(1- \beta)}}} \\ & = \frac{1}{(1- \beta)^{\frac{1}{1- \beta}} \lambda^{\frac{N'}{1- \beta}}}. \end{align*}Thus,
\begin{align*} P_{N,\beta}(u) & = \frac{1}{\left(1- \left\|u\right\|_{E_{q,\beta}}^N\right)^{\frac{1}{(N-1)(1- \beta)}}} = \frac{1}{\left((1- \beta)^{N-1} \lambda^N\right)^{\frac{1}{(N-1)(1- \beta)}}} \\ & = \frac{1}{(1- \beta)^{\frac{1}{1- \beta}} \lambda^{\frac{N'}{1- \beta}}}. \end{align*}Thus, \[ \theta_k\left(a\left((1/2)^{1- \beta} \!-\! (1/4)^{1- \beta}\right)^{\frac{1}{N'}} \!+\! \lambda \left(k^{1- \beta} \!-\! (1/2)^{1- \beta}\right)^{\frac{1}{N'}}\right)^{\frac{N'}{1- \beta}} \mathop{\sim}\limits_{k \to + \infty} (1\!+\! \epsilon) N k. \]For $0 \leq j \leq j_{\beta }-1,$
\[ \theta_k\left(a\left((1/2)^{1- \beta} \!-\! (1/4)^{1- \beta}\right)^{\frac{1}{N'}} \!+\! \lambda \left(k^{1- \beta} \!-\! (1/2)^{1- \beta}\right)^{\frac{1}{N'}}\right)^{\frac{N'}{1- \beta}} \mathop{\sim}\limits_{k \to + \infty} (1\!+\! \epsilon) N k. \]For $0 \leq j \leq j_{\beta }-1,$
 we have
\[ \int_{\mathbb{R}^N} \left|v_k\right|^{\frac{jN'}{1- \beta}}\,{\rm d}x = \omega_{N-1}^{1- \frac{j}{(N-1)(1- \beta)}} \int_{1/4}^{+ \infty} \left| \psi(t) + \psi_k(t)\right|^{\frac{jN'}{1- \beta}}\,{\rm e}^{{-}Nt}\,{\rm d}t. \]Hence,
we have
\[ \int_{\mathbb{R}^N} \left|v_k\right|^{\frac{jN'}{1- \beta}}\,{\rm d}x = \omega_{N-1}^{1- \frac{j}{(N-1)(1- \beta)}} \int_{1/4}^{+ \infty} \left| \psi(t) + \psi_k(t)\right|^{\frac{jN'}{1- \beta}}\,{\rm e}^{{-}Nt}\,{\rm d}t. \]Hence, \[ \sup_{k \geq 1} \frac{1}{\left\|v_k\right\|_{E_{q, \beta}}^{\frac{jN'}{1- \beta}}} \int_{\mathbb{R}^N} \left|v_k\right|^{\frac{jN'}{1- \beta}}\,{\rm d}x <{+} \infty. \]We finally deduce from (6.13) that
\[ \sup_{k \geq 1} \frac{1}{\left\|v_k\right\|_{E_{q, \beta}}^{\frac{jN'}{1- \beta}}} \int_{\mathbb{R}^N} \left|v_k\right|^{\frac{jN'}{1- \beta}}\,{\rm d}x <{+} \infty. \]We finally deduce from (6.13) that \begin{align*} & \int_{\mathbb{R}^N} \left({\rm e}^{\alpha_{N, \beta} p \left| \frac{v_k}{\left\|v_k\right\|_{E_{q,\beta}}}\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p \left| \frac{v_k}{\left\|v_k\right\|_{E_{q,\beta}}}\right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x \\ & \quad \to +\infty,\ k \to + \infty. \end{align*}
\begin{align*} & \int_{\mathbb{R}^N} \left({\rm e}^{\alpha_{N, \beta} p \left| \frac{v_k}{\left\|v_k\right\|_{E_{q,\beta}}}\right|^{\frac{N'}{1- \beta}}} -S_{j_{\beta}-1}\left(\alpha_{N, \beta} p \left| \frac{v_k}{\left\|v_k\right\|_{E_{q,\beta}}}\right|^{\frac{N'}{1- \beta}}\right)\right) {\rm d}x \\ & \quad \to +\infty,\ k \to + \infty. \end{align*}
2. Now, we treat the case $\beta = 1.$
 For the first part of the proof (i.e., inequality (1.27)), we can adapt the contradiction argument used for the case $\beta < 1.$
For the first part of the proof (i.e., inequality (1.27)), we can adapt the contradiction argument used for the case $\beta < 1.$ But, due to the existence of some essential technical difference, we give the proof with a minimum of details. Observing that, as previously, the case $\left \|u\right \|_{E_{q,1}} = 1$
But, due to the existence of some essential technical difference, we give the proof with a minimum of details. Observing that, as previously, the case $\left \|u\right \|_{E_{q,1}} = 1$ can be easily studied using the uniform convexity of the functional space $E_{q,1},$
can be easily studied using the uniform convexity of the functional space $E_{q,1},$ we can assume that $0 < \left \|u\right \|_{E_{q,1}} < 1.$
we can assume that $0 < \left \|u\right \|_{E_{q,1}} < 1.$ Assume by contradiction that there exists $0 < p_1 < \left (\frac {1}{1- \left \|u\right \|_{E_{q,1}}^N}\right )^{\frac {1}{N-1}}$
Assume by contradiction that there exists $0 < p_1 < \left (\frac {1}{1- \left \|u\right \|_{E_{q,1}}^N}\right )^{\frac {1}{N-1}}$ such that
\begin{align*} & \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p_1 \left|u_n\right|^{N'}} -1\right)} - S_{j_1-1}\left(N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p_1 \left|u_n\right|^{N'}} -1\right)\right)\right) {\rm d}x \\ & \quad ={+} \infty. \end{align*}Arguing as for the case $0 < \beta < 1,$
such that
\begin{align*} & \sup_n \int_{\mathbb{R}^N} \left({\rm e}^{N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p_1 \left|u_n\right|^{N'}} -1\right)} - S_{j_1-1}\left(N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p_1 \left|u_n\right|^{N'}} -1\right)\right)\right) {\rm d}x \\ & \quad ={+} \infty. \end{align*}Arguing as for the case $0 < \beta < 1,$
 we can easily find $\epsilon > 0$
we can easily find $\epsilon > 0$ small enough and $L$
small enough and $L$ large enough such that
(6.14)\begin{align} & \limsup_{n \to + \infty} \left(\int_{\mathbb{R}^N} \left| \nabla T_L(u_n)\right|^N w_{1}(x)\,{\rm d}x+ \left(\int_{\mathbb{R}^N} \left| \nabla T_L(u_n)\right|^q\,{\rm d}x\right)^{\frac{N}{q}}\right)\nonumber\\ & \quad < \left( \frac{1}{p_1(1+ \epsilon)^2}\right)^{N-1}. \end{align}Here, the function $T_L$
large enough such that
(6.14)\begin{align} & \limsup_{n \to + \infty} \left(\int_{\mathbb{R}^N} \left| \nabla T_L(u_n)\right|^N w_{1}(x)\,{\rm d}x+ \left(\int_{\mathbb{R}^N} \left| \nabla T_L(u_n)\right|^q\,{\rm d}x\right)^{\frac{N}{q}}\right)\nonumber\\ & \quad < \left( \frac{1}{p_1(1+ \epsilon)^2}\right)^{N-1}. \end{align}Here, the function $T_L$
 is defined by (6.2). Set again $\Omega _{n,L} = \left \{x \in \mathbb {R}^N,\ \left |u_n(x)\right |\right.\left. \geq L\right \}.$
is defined by (6.2). Set again $\Omega _{n,L} = \left \{x \in \mathbb {R}^N,\ \left |u_n(x)\right |\right.\left. \geq L\right \}.$ Using (3.3) and Young's inequality, it yields
(6.15)\begin{align} & \int_{\Omega_{n,L} \cap \mathcal{B}} \left({\rm e}^{N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}p_1 \left|u_n\right|^{N'}} -1\right)} - S_{j_1-1} \left(N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}p_1 \left|u_n\right|^{N'}} -1\right)\right)\right) {\rm d}x \nonumber\\ & \leq \int_{\Omega_{n,L} \cap \mathcal{B}} {\rm e}^{N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}p_1 \left|u_n\right|^{N'}} -1\right)} {\rm d}x \nonumber\\ & \leq {\rm e}^{{-}N} \int_{\Omega_{n,L} \cap \mathcal{B}}\,{\rm e}^{N {\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} (1+ \epsilon)p_1 \left|u_n-L\right|^{N'}}\,{\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p_1 A_1(\epsilon) L^{N'}}}\,{\rm d}x \nonumber\\ & \leq \int_{\Omega_{n,L} \cap \mathcal{B}} \exp \left(N \left[\frac{{\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p_1 (1+ \epsilon)^2 \left|T_L(u_n)\right|^{N'}}}{1+ \epsilon} + \frac{\epsilon}{1+ \epsilon}\,{\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p_1 \frac{1+ \epsilon}{\epsilon} A_1( \epsilon) L^{N'}}\right]\right) {\rm d}x \nonumber\\ & \leq {\rm e}^{N\,{\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p_1 \frac{1+ \epsilon}{\epsilon} A_1( \epsilon) L^{N'}}} \int_{\mathcal{B}}\,{\rm e}^{N\,{\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p_1 (1+ \epsilon)^2 \left|T_L(u_n)\right|^{N'}}}\,{\rm d}x, \end{align}where $A_1( \epsilon ) = \frac {1+ \epsilon }{((1+ \epsilon )^{\frac {1}{N-1}} -1)^{N-1}}.$
Using (3.3) and Young's inequality, it yields
(6.15)\begin{align} & \int_{\Omega_{n,L} \cap \mathcal{B}} \left({\rm e}^{N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}p_1 \left|u_n\right|^{N'}} -1\right)} - S_{j_1-1} \left(N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}p_1 \left|u_n\right|^{N'}} -1\right)\right)\right) {\rm d}x \nonumber\\ & \leq \int_{\Omega_{n,L} \cap \mathcal{B}} {\rm e}^{N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}p_1 \left|u_n\right|^{N'}} -1\right)} {\rm d}x \nonumber\\ & \leq {\rm e}^{{-}N} \int_{\Omega_{n,L} \cap \mathcal{B}}\,{\rm e}^{N {\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} (1+ \epsilon)p_1 \left|u_n-L\right|^{N'}}\,{\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p_1 A_1(\epsilon) L^{N'}}}\,{\rm d}x \nonumber\\ & \leq \int_{\Omega_{n,L} \cap \mathcal{B}} \exp \left(N \left[\frac{{\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p_1 (1+ \epsilon)^2 \left|T_L(u_n)\right|^{N'}}}{1+ \epsilon} + \frac{\epsilon}{1+ \epsilon}\,{\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p_1 \frac{1+ \epsilon}{\epsilon} A_1( \epsilon) L^{N'}}\right]\right) {\rm d}x \nonumber\\ & \leq {\rm e}^{N\,{\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p_1 \frac{1+ \epsilon}{\epsilon} A_1( \epsilon) L^{N'}}} \int_{\mathcal{B}}\,{\rm e}^{N\,{\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p_1 (1+ \epsilon)^2 \left|T_L(u_n)\right|^{N'}}}\,{\rm d}x, \end{align}where $A_1( \epsilon ) = \frac {1+ \epsilon }{((1+ \epsilon )^{\frac {1}{N-1}} -1)^{N-1}}.$
 By (6.14), we know that
\[ \int_{\mathcal{B}} \left| \nabla (p_1(1+ \epsilon)^2)^{\frac{1}{N'}} T_L(u_n)\right|^N w_1(x)\,{\rm d}x < 1. \]Using (1.4), we get
By (6.14), we know that
\[ \int_{\mathcal{B}} \left| \nabla (p_1(1+ \epsilon)^2)^{\frac{1}{N'}} T_L(u_n)\right|^N w_1(x)\,{\rm d}x < 1. \]Using (1.4), we get \[ \sup_n \int_{\mathcal{B}}\,{\rm e}^{N\,{\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p_1 (1+ \epsilon)^2 \left|T_L(u_n)\right|^{N'}}}\,{\rm d}x <{+} \infty. \]By (6.15), we obtain
\[ \sup_n \int_{\mathcal{B}}\,{\rm e}^{N\,{\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p_1 (1+ \epsilon)^2 \left|T_L(u_n)\right|^{N'}}}\,{\rm d}x <{+} \infty. \]By (6.15), we obtain \begin{align*} & \sup_n \int_{\Omega_{n,L} \cap \mathcal{B}} \left({\rm e}^{N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}p_1 \left|u_n\right|^{N'}} -1\right)} \right.\nonumber\\ & \left.\quad -\, S_{j_1-1} \left(N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}p_1 \left|u_n\right|^{N'}} -1\right)\right)\vphantom{\left({\rm e}^{N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}p_1 \left|u_n\right|^{N'}} -1\right)} \right.}\right) {\rm d}x <{+} \infty. \end{align*}The boundedness of the sequence
\begin{align*} & \sup_n \int_{\Omega_{n,L} \cap \mathcal{B}} \left({\rm e}^{N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}p_1 \left|u_n\right|^{N'}} -1\right)} \right.\nonumber\\ & \left.\quad -\, S_{j_1-1} \left(N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}p_1 \left|u_n\right|^{N'}} -1\right)\right)\vphantom{\left({\rm e}^{N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}p_1 \left|u_n\right|^{N'}} -1\right)} \right.}\right) {\rm d}x <{+} \infty. \end{align*}The boundedness of the sequence \[ \int_{\Omega_{n,L}^c} \left({\rm e}^{N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}p_1 \left|u_n\right|^{N'}} -1\right)} - S_{j_1-1} \left(N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}p_1 \left|u_n\right|^{N'}} -1\right)\right)\right) {\rm d}x, \]can be established by proceeding as for the case $0 < \beta < 1$
\[ \int_{\Omega_{n,L}^c} \left({\rm e}^{N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}p_1 \left|u_n\right|^{N'}} -1\right)} - S_{j_1-1} \left(N \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}}p_1 \left|u_n\right|^{N'}} -1\right)\right)\right) {\rm d}x, \]can be established by proceeding as for the case $0 < \beta < 1$
 and the details are omitted. In order to prove (1.28), we consider the sequence of functions $\psi _k: \mathbb {R} \rightarrow \mathbb {R}$
and the details are omitted. In order to prove (1.28), we consider the sequence of functions $\psi _k: \mathbb {R} \rightarrow \mathbb {R}$ defined by
(6.16)\begin{equation} \psi_k(t) = \left\{\begin{array}{ll} \dfrac{\log(t+1) - \log (3/2)}{\left(\log(k+1) - \log(3/2)\right)^{\dfrac{1}{N}}}, & 1/2 \leq t \leq k, \\ \left(\log(k+1) -\log (3/2)\right)^{\dfrac{1}{N'}}, & t \geq k, \\ 0, & t \leq 1/2. \end{array} \right. \end{equation}We also define the function $\psi :\mathbb {R} \to \mathbb {R}$
defined by
(6.16)\begin{equation} \psi_k(t) = \left\{\begin{array}{ll} \dfrac{\log(t+1) - \log (3/2)}{\left(\log(k+1) - \log(3/2)\right)^{\dfrac{1}{N}}}, & 1/2 \leq t \leq k, \\ \left(\log(k+1) -\log (3/2)\right)^{\dfrac{1}{N'}}, & t \geq k, \\ 0, & t \leq 1/2. \end{array} \right. \end{equation}We also define the function $\psi :\mathbb {R} \to \mathbb {R}$
 by
\[ \psi(t) = \left\{\begin{array}{ll} 0, & t \leq 1/4, \\ \dfrac{\log(t+1) - \log(5/4)}{\left(\log(3/2) - \log(5/4)\right)^{\dfrac{1}{N}}}, & 1/4 \leq t \leq 1/2, \\ \left(\log(3/2) - \log(5/4)\right)^{\dfrac{1}{N'}}, & t \geq 1/2. \end{array} \right. \]Set, as for the first case, $u_k(x) = \omega _{N-1}^{- \frac {1}{N}} \psi _k(t)$
by
\[ \psi(t) = \left\{\begin{array}{ll} 0, & t \leq 1/4, \\ \dfrac{\log(t+1) - \log(5/4)}{\left(\log(3/2) - \log(5/4)\right)^{\dfrac{1}{N}}}, & 1/4 \leq t \leq 1/2, \\ \left(\log(3/2) - \log(5/4)\right)^{\dfrac{1}{N'}}, & t \geq 1/2. \end{array} \right. \]Set, as for the first case, $u_k(x) = \omega _{N-1}^{- \frac {1}{N}} \psi _k(t)$
 and $u(x) = \omega _{N-1}^{- \frac {1}{N}} \psi (t),\ \left |x\right | = {\rm e}^{-t}.$
and $u(x) = \omega _{N-1}^{- \frac {1}{N}} \psi (t),\ \left |x\right | = {\rm e}^{-t}.$ Observe that
\[ \int_{\mathbb{R}^N} \left|\nabla u_k\right|^{q}\,{\rm d}x \to 0,\ k \to + \infty. \]Set, $v_k = u + u_k.$
Observe that
\[ \int_{\mathbb{R}^N} \left|\nabla u_k\right|^{q}\,{\rm d}x \to 0,\ k \to + \infty. \]Set, $v_k = u + u_k.$
 We have,
\[ \left\|v_k\right\|_{E_{q,1}}^N = \left\|u_k +u\right\|_{E_{q,1}}^N= 2 + \left(\int_{\mathbb{R}^N} \left| \nabla u_k\right|^q\,{\rm d}x + \int_{\mathbb{R}^N} \left|\nabla u\right|^q\,{\rm d}x \right)^{\frac{N}{q}}. \]Thus,
We have,
\[ \left\|v_k\right\|_{E_{q,1}}^N = \left\|u_k +u\right\|_{E_{q,1}}^N= 2 + \left(\int_{\mathbb{R}^N} \left| \nabla u_k\right|^q\,{\rm d}x + \int_{\mathbb{R}^N} \left|\nabla u\right|^q\,{\rm d}x \right)^{\frac{N}{q}}. \]Thus, \[ \left\|v_k\right\|_{E_{q,1}}^N \to 2 + \left( \int_{\mathbb{R}^N} \left| \nabla u\right|^q\,{\rm d}x\right)^{\frac{N}{q}} =1+ \left\|u\right\|_{E_{q,1}}^N. \]Since $u_k \rightharpoonup 0$
\[ \left\|v_k\right\|_{E_{q,1}}^N \to 2 + \left( \int_{\mathbb{R}^N} \left| \nabla u\right|^q\,{\rm d}x\right)^{\frac{N}{q}} =1+ \left\|u\right\|_{E_{q,1}}^N. \]Since $u_k \rightharpoonup 0$
 weakly in $E_{q,1},$
weakly in $E_{q,1},$ then
\[ \frac{v_k}{\left\|v_k\right\|_{E_{q,1}}} \rightharpoonup \widetilde{u} = \frac{u}{\left(1 + \left\|u\right\|_{E_{q,1}}^N\right)^{\frac{1}{N}}}. \]Let $\alpha > 0$
then
\[ \frac{v_k}{\left\|v_k\right\|_{E_{q,1}}} \rightharpoonup \widetilde{u} = \frac{u}{\left(1 + \left\|u\right\|_{E_{q,1}}^N\right)^{\frac{1}{N}}}. \]Let $\alpha > 0$
 and $p > P_{N,1}(\widetilde {u}) = (1 + \left \|u\right \|_{E_{q,1}}^N)^{\frac {1}{N-1}}.$
and $p > P_{N,1}(\widetilde {u}) = (1 + \left \|u\right \|_{E_{q,1}}^N)^{\frac {1}{N-1}}.$ We have
(6.17)\begin{align} & \int_{\mathbb{R}^N} \left({\rm e}^{\alpha \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p\left| \frac{v_k(x)}{\left\|v_k\right\|_{E_{q,1}}}\right|^{N'}} -1\right)}-S_{j_1-1}\left(\alpha \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p\left| \frac{v_k(x)}{\left\|v_k\right\|_{E_{q,1}}}\right|^{N'}} -1\right)\right)\right) {\rm d}x \nonumber\\ & \geq \omega_{N-1} \int_k^{+ \infty}\,{\rm e}^{\alpha \left({\rm e}^{p\frac{ \log(k+1) - \log(3/2)}{\left(2 + \left(\left|\nabla u\right|_{L^{q}( \mathbb{R}^N)}^{q} + \left|\nabla u_k\right|_{L^q( \mathbb{R}^N)}^{q}\right)^{\frac{N}{q}} \right)^{\frac{1}{N-1}}}}-1\right)}{\rm e}^{{-}Nt} \,{\rm d}t\nonumber\\ & \quad - \int_{\mathbb{R}^N} S_{j_1-1}\left(\alpha \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p\left| \frac{v_k(x)}{\left\|v_k\right\|_{E_{q,1}}}\right|^{N'}} -1\right)\right) {\rm d}x \nonumber\\ & = \omega_{N-1}\,{\rm e}^{\alpha \left({\rm e}^{p\frac{ \log(k+1) - \log(3/2)}{\left(2 + \left(\left|\nabla u\right|_{L^{q}( \mathbb{R}^N)}^{q} + \left|\nabla u_k\right|_{L^q( \mathbb{R}^N)}^{q}\right)^{\frac{N}{q}} \right)^{\frac{1}{N-1}}}}-1\right)}\frac{{\rm e}^{{-}Nk}}{N} \nonumber\\ & \quad - \int_{\mathbb{R}^N} S_{j_1-1}\left(\alpha \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p\left| \frac{v_k(x)}{\left\|v_k\right\|_{E_{q,1}}}\right|^{N'}} -1\right)\right) {\rm d}x. \end{align}Since $p > (1 + \left \|u\right \|_{E_{q,1}}^N)^{\frac {1}{N-1}},$
We have
(6.17)\begin{align} & \int_{\mathbb{R}^N} \left({\rm e}^{\alpha \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p\left| \frac{v_k(x)}{\left\|v_k\right\|_{E_{q,1}}}\right|^{N'}} -1\right)}-S_{j_1-1}\left(\alpha \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p\left| \frac{v_k(x)}{\left\|v_k\right\|_{E_{q,1}}}\right|^{N'}} -1\right)\right)\right) {\rm d}x \nonumber\\ & \geq \omega_{N-1} \int_k^{+ \infty}\,{\rm e}^{\alpha \left({\rm e}^{p\frac{ \log(k+1) - \log(3/2)}{\left(2 + \left(\left|\nabla u\right|_{L^{q}( \mathbb{R}^N)}^{q} + \left|\nabla u_k\right|_{L^q( \mathbb{R}^N)}^{q}\right)^{\frac{N}{q}} \right)^{\frac{1}{N-1}}}}-1\right)}{\rm e}^{{-}Nt} \,{\rm d}t\nonumber\\ & \quad - \int_{\mathbb{R}^N} S_{j_1-1}\left(\alpha \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p\left| \frac{v_k(x)}{\left\|v_k\right\|_{E_{q,1}}}\right|^{N'}} -1\right)\right) {\rm d}x \nonumber\\ & = \omega_{N-1}\,{\rm e}^{\alpha \left({\rm e}^{p\frac{ \log(k+1) - \log(3/2)}{\left(2 + \left(\left|\nabla u\right|_{L^{q}( \mathbb{R}^N)}^{q} + \left|\nabla u_k\right|_{L^q( \mathbb{R}^N)}^{q}\right)^{\frac{N}{q}} \right)^{\frac{1}{N-1}}}}-1\right)}\frac{{\rm e}^{{-}Nk}}{N} \nonumber\\ & \quad - \int_{\mathbb{R}^N} S_{j_1-1}\left(\alpha \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p\left| \frac{v_k(x)}{\left\|v_k\right\|_{E_{q,1}}}\right|^{N'}} -1\right)\right) {\rm d}x. \end{align}Since $p > (1 + \left \|u\right \|_{E_{q,1}}^N)^{\frac {1}{N-1}},$
 then
\[ \lim_{k \to + \infty} \left(p\frac{ \log(k+1) - \log(3/2)}{\left(2 + \left(\left|\nabla u\right|_{L^{q}( \mathbb{R}^N)}^{q} + \left|\nabla u_k\right|_{L^q( \mathbb{R}^N)}^{q}\right)^{\frac{N}{q}} \right)^{\frac{1}{N-1}}} -\log k\right) ={+} \infty. \]It follows,
then
\[ \lim_{k \to + \infty} \left(p\frac{ \log(k+1) - \log(3/2)}{\left(2 + \left(\left|\nabla u\right|_{L^{q}( \mathbb{R}^N)}^{q} + \left|\nabla u_k\right|_{L^q( \mathbb{R}^N)}^{q}\right)^{\frac{N}{q}} \right)^{\frac{1}{N-1}}} -\log k\right) ={+} \infty. \]It follows, \[ \alpha \left({\rm e}^{p\frac{ \log(k+1) - \log(3/2)}{\left(2 + \left(\left|\nabla u\right|_{L^{q}( \mathbb{R}^N)}^{q} + \left|\nabla u_k\right|_{L^q( \mathbb{R}^N)}^{q}\right)^{\frac{N}{q}} \right)^{\frac{1}{N-1}}}}-1\right) -Nk \to + \infty,\ k \to + \infty. \]Finally, one can easily show that
\[ \alpha \left({\rm e}^{p\frac{ \log(k+1) - \log(3/2)}{\left(2 + \left(\left|\nabla u\right|_{L^{q}( \mathbb{R}^N)}^{q} + \left|\nabla u_k\right|_{L^q( \mathbb{R}^N)}^{q}\right)^{\frac{N}{q}} \right)^{\frac{1}{N-1}}}}-1\right) -Nk \to + \infty,\ k \to + \infty. \]Finally, one can easily show that \[ \sup_{k \geq 1} \int_{\mathbb{R}^N} S_{j_1-1}\left(\alpha \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p\left| \frac{v_k(x)}{\left\|v_k\right\|_{E_{q,1}}}\right|^{N'}} -1\right)\right) {\rm d}x <{+} \infty. \]In view of (6.17), we deduce that (1.28) holds. This ends the proof of theorem 1.5.
\[ \sup_{k \geq 1} \int_{\mathbb{R}^N} S_{j_1-1}\left(\alpha \left({\rm e}^{\omega_{N-1}^{\frac{1}{N-1}} p\left| \frac{v_k(x)}{\left\|v_k\right\|_{E_{q,1}}}\right|^{N'}} -1\right)\right) {\rm d}x <{+} \infty. \]In view of (6.17), we deduce that (1.28) holds. This ends the proof of theorem 1.5.
7. Proof of theorem 1.6
We start with the case $0 < \beta < 1.$![]() As in the proof of theorem 1.5, we argue by contradiction. So, assume that there exists $0 < p_1 < (\frac {1}{1- \left \|u\right \|_{q,\beta }})^{\frac {N'}{q( 1- \beta )}}$
As in the proof of theorem 1.5, we argue by contradiction. So, assume that there exists $0 < p_1 < (\frac {1}{1- \left \|u\right \|_{q,\beta }})^{\frac {N'}{q( 1- \beta )}}$![]() such that
such that
The function $T_L$![]() and $G_L$
and $G_L$![]() being defined by (6.2), it is easy to see that there exist $0 < \epsilon < 1$
being defined by (6.2), it is easy to see that there exist $0 < \epsilon < 1$![]() small enough and $L > 0$
small enough and $L > 0$![]() large enough such that
large enough such that
The keystone of the proof is to establish the inequality

For that aim, we argue once again by contradiction. So, we assume that there exists a subsequence of $(u_n)_n,$![]() still denoted by $(u_n)_n,$
still denoted by $(u_n)_n,$![]() such that
such that

First, observe that the general form of (2.8) is given by the following inequality
where $D_t(\delta ) = \frac {1+ \delta }{((1+ \delta )^{\frac {1}{t-1}}-1)^{t-1}}.$![]() From that last inequality, we can easily deduce another useful inequality, that is
From that last inequality, we can easily deduce another useful inequality, that is
Let $\delta > 0.$![]() Applying (7.4), we obtain
Applying (7.4), we obtain

In a similar way, we have

A simple analysis shows that the function defined on $]1, + \infty [$![]() by
by

where $z$![]() is some fixed real number such that $z > 1,$
is some fixed real number such that $z > 1,$![]() is nondecreasing. Thus,
is nondecreasing. Thus,

Putting (7.3) in that last inequality and using the fact that
we infer

Now, consider the function defined on $]1, + \infty [$![]() by
by

A quick analysis of this function shows that it attains its maximum at the point

and this maximum is

Hence,

Consequently, the function defined on $]0, + \infty [$![]() by
by

attains its maximum at the point $\delta _0 > 0$![]() given by the identity
given by the identity

and this maximum is

Thus, choosing $\delta = \delta _0$![]() in (7.7), it comes
in (7.7), it comes

which is in contradiction with (7.1). Therefore, (7.2) holds. The rest of the proof is similar to what has been done in the proof of theorem 1.5 (with suitable adaptation) and, in order to avoid redundancy, the details will be omitted. For the case $\beta = 1,$![]() we can easily adapt the same arguments used previously for the case $0 < \beta < 1$
we can easily adapt the same arguments used previously for the case $0 < \beta < 1$![]() to prove that there exists $\epsilon > 0$
to prove that there exists $\epsilon > 0$![]() small enough and $L > 0$
small enough and $L > 0$![]() large enough such that
large enough such that

The rest of the proof of (1.31) is similar to the proof of (1.27) and will be omitted. The same can be said concerning (1.32) whose proof is similar to (1.28). This ends the proof of theorem 1.6.
8. Applications to some elliptic equations
In this section, we deal with the following elliptic equation:
where $f : \mathbb {R} \rightarrow \mathbb {R}$![]() is a continuous function such that $f(s) = 0,\ \forall \ s \leq 0.$
is a continuous function such that $f(s) = 0,\ \forall \ s \leq 0.$![]() Here, we assume that the weight given by (1.13) satisfies
Here, we assume that the weight given by (1.13) satisfies
By this assumption, it yields $E_{q, 1} \hookrightarrow E_r^{N,q}$![]() with continuous embedding where $E^{N,q}_r$
with continuous embedding where $E^{N,q}_r$![]() is defined in [Reference Carvalho, Figueiredo, Furtado and Medeiros19] as the subspace of radial functions of the completion of $C_0^{\infty }( \mathbb {R}^N)$
is defined in [Reference Carvalho, Figueiredo, Furtado and Medeiros19] as the subspace of radial functions of the completion of $C_0^{\infty }( \mathbb {R}^N)$![]() with respect to the norm
with respect to the norm

By [Reference Carvalho, Figueiredo, Furtado and Medeiros19, proposition 2.1], we know that $E_r^{N,q}$![]() is continuously (resp. compactly) embedded into $L^t( \mathbb {R}^N),\ \forall \ q^* \leq t < + \infty$
is continuously (resp. compactly) embedded into $L^t( \mathbb {R}^N),\ \forall \ q^* \leq t < + \infty$![]() (resp. $\forall \ q^* < t < + \infty ).$
(resp. $\forall \ q^* < t < + \infty ).$![]() Consequently, the embedding $E_{q,1} \hookrightarrow L^t( \mathbb {R}^N)$
Consequently, the embedding $E_{q,1} \hookrightarrow L^t( \mathbb {R}^N)$![]() is continuous for $q^* \leq t < + \infty$
is continuous for $q^* \leq t < + \infty$![]() and compact for $q^* < t < + \infty.$
and compact for $q^* < t < + \infty.$![]() We assume that $f$
We assume that $f$![]() has a critical double exponential growth at infinity, that is there exists a constant $\alpha _0 > 0$
has a critical double exponential growth at infinity, that is there exists a constant $\alpha _0 > 0$![]() such that
such that
We also assume that: $(F_1)$![]() There exists $\theta > N$
There exists $\theta > N$![]() such that
such that
$(F_2)$![]() There exist $C > 0,\ s_1 > 0$
There exist $C > 0,\ s_1 > 0$![]() and $p > \max \left \{q^*,N\right \}$
and $p > \max \left \{q^*,N\right \}$![]() such that
such that
$(F_3)$![]() There exist $A > 0$
There exist $A > 0$![]() and $r > q$
and $r > q$![]() such that
such that
Example An example of a function $f$![]() satisfying the conditions $(F_1)-(F_3)$
satisfying the conditions $(F_1)-(F_3)$![]() is given by: $f(s) = F'(s),$
is given by: $f(s) = F'(s),$![]() where
where

with $\alpha > 0,\ m > \max \left \{N,q^*\right \}$![]() . A radial weak solution of the equation (8.1) is a function $u \in E_{q,1}$
. A radial weak solution of the equation (8.1) is a function $u \in E_{q,1}$![]() such that
such that
Theorem 8.1 Assume that $(F_1)-(F_3)$![]() hold. Then, there exists $A_0 > 0$
hold. Then, there exists $A_0 > 0$![]() such that the equation (8.1) has at least one nontrivial and nonnegative radial weak solution for all $A > A_0.$
such that the equation (8.1) has at least one nontrivial and nonnegative radial weak solution for all $A > A_0.$![]()
The energy functional associated to (8.1) is
Lemma 8.2 Assume that $(F_1)$![]() and $(F_2)$
and $(F_2)$![]() hold. Then, the functional $I$
hold. Then, the functional $I$![]() satisfies the $(PS)_c$
satisfies the $(PS)_c$![]() condition for all $c < \left (\frac {1}{N} - \frac {1}{\theta }\right )\min \left \{1, \frac {\omega _{N-1}}{\alpha _0^{N-1}2^{N-1}}\right \}.$
condition for all $c < \left (\frac {1}{N} - \frac {1}{\theta }\right )\min \left \{1, \frac {\omega _{N-1}}{\alpha _0^{N-1}2^{N-1}}\right \}.$![]()
Proof. For the simplicity in notation, set
Let $(u_n)_n \subset E_{q,1}$![]() be a (PS) sequence of $I$
be a (PS) sequence of $I$![]() at a level $c < \left (\frac {1}{N} - \frac {1}{\theta }\right )\min \left \{1, \frac {\omega _{N-1}}{\alpha _0^{N-1}2^{N-1}}\right \}.$
at a level $c < \left (\frac {1}{N} - \frac {1}{\theta }\right )\min \left \{1, \frac {\omega _{N-1}}{\alpha _0^{N-1}2^{N-1}}\right \}.$![]() It yields
It yields

where $o_n(1)$![]() stands for any sequence of nonnegative real numbers converging to zero when $n$
stands for any sequence of nonnegative real numbers converging to zero when $n$![]() tends to $+ \infty.$
tends to $+ \infty.$![]() Since $\theta > N > q,$
Since $\theta > N > q,$![]() from $(F_1)$
from $(F_1)$![]() we can immediately deduce that $(u_n)_n$
we can immediately deduce that $(u_n)_n$![]() is bounded. Moreover,
is bounded. Moreover,
Taking into account that $\frac {N \theta c}{\theta -N} < 1,$![]() we deduce from (8.3) that, up to a subsequence,
we deduce from (8.3) that, up to a subsequence,
Thus,

Putting that last inequality in (8.3), we get
Then, there exist $\epsilon _0,\ \epsilon _1 > 0$![]() and a subsequence of $(u_n)_n,$
and a subsequence of $(u_n)_n,$![]() still denoted by $(u_n)_n,$
still denoted by $(u_n)_n,$![]() such that
such that

Let $u \in E_{q,1}$![]() be the weak limit of $(u_n)_n$
be the weak limit of $(u_n)_n$![]() in $E_{q,1}.$
in $E_{q,1}.$![]() We claim that, up to a subsequence, $u_n \to u$
We claim that, up to a subsequence, $u_n \to u$![]() strongly in $E_{q,1}.$
strongly in $E_{q,1}.$![]() Let $t > q^*-1.$
Let $t > q^*-1.$![]() By (8.2) and $(F_2),$
By (8.2) and $(F_2),$![]() we have
we have

Clearly, there exist $c_{8} > 0$![]() and $s_2 > 0$
and $s_2 > 0$![]() such that
such that

Hence,

Plainly, there exists a positive constant $\kappa$![]() such that
such that
Then, we can derive that

Having in mind that if $j \geq j_1,$![]() then $N'j \geq q^*,$
then $N'j \geq q^*,$![]() it follows from (8.6) that
it follows from (8.6) that

Hence, there exists a positive constant $c_9 > 0$![]() such that
such that
Putting that last inequality in (8.5), we get

Using (1.22), it yields
Now, since $t+1 > q^*$![]() and $p > q^*,$
and $p > q^*,$![]() then the embeddings $E_{q,1} \hookrightarrow L^{t+1}( \mathbb {R}^N)$
then the embeddings $E_{q,1} \hookrightarrow L^{t+1}( \mathbb {R}^N)$![]() and $E_{q,1} \hookrightarrow L^p(\mathbb {R}^N)$
and $E_{q,1} \hookrightarrow L^p(\mathbb {R}^N)$![]() are compact. It follows from (8.4) that
are compact. It follows from (8.4) that
Taking into account that

we infer $u_n \to 0$![]() strongly in $E_{q,1}.$
strongly in $E_{q,1}.$![]() This ends the proof of lemma 8.2.
This ends the proof of lemma 8.2.
Now, we claim that there exist $\rho _0 > 0,\ \rho _1 > 0,\ e_0 \in E_{q,1}$![]() such that $\left \|e_0\right \|_{q,1} > \rho _0 ,\ I(e_0) < 0,$
such that $\left \|e_0\right \|_{q,1} > \rho _0 ,\ I(e_0) < 0,$![]() and
and
Given $u \in E_{q,1}$![]() and $t > p.$
and $t > p.$![]() By (8.2) and $(F_2),$
By (8.2) and $(F_2),$![]() we have
we have

For $u \in E_{q,1}$![]() such that $\left \|u\right \|_{q,1} = \rho _0 < \min \left \{1,\ \left (\frac {\omega _{N-1}^{\frac {1}{N-1}}}{3 \alpha _0}\right )^{\frac {1}{N'}}\right \},$
such that $\left \|u\right \|_{q,1} = \rho _0 < \min \left \{1,\ \left (\frac {\omega _{N-1}^{\frac {1}{N-1}}}{3 \alpha _0}\right )^{\frac {1}{N'}}\right \},$ by (1.22), there exists a constant $c_{14} > 0$
by (1.22), there exists a constant $c_{14} > 0$![]() such that
such that

Putting that inequality in (8.7), for $u \in E_{q,1}$![]() such that $\left \|u\right \|_{q,1} = \rho _0,$
such that $\left \|u\right \|_{q,1} = \rho _0,$![]() it yields
it yields

Plainly, one could choose $\rho _0$![]() small enough such that $\rho _0 < \left (\frac {2^{1-N}}{2Nc_{15}}\right )^{\frac {1}{p-N}}.$
small enough such that $\rho _0 < \left (\frac {2^{1-N}}{2Nc_{15}}\right )^{\frac {1}{p-N}}.$![]() By (8.8), we deduce that
By (8.8), we deduce that
Now, for a fixed $\phi \in C_{0,rad}^{\infty }( \mathbb {R}^N) \backslash {\left \{0\right \}}$![]() such that $\phi \geq 0,$
such that $\phi \geq 0,$![]() we have
we have
In fact, from the hypothesis $(F_1),$![]() one can see that there exist two positive constants $c_{16}$
one can see that there exist two positive constants $c_{16}$![]() and $c_{17}$
and $c_{17}$![]() such that
such that
Let
the mountain pass level of the functional $I.$![]() In order to complete the proof of theorem 8.1, it suffices to show that there exists $A_0 > 0$
In order to complete the proof of theorem 8.1, it suffices to show that there exists $A_0 > 0$![]() such that
such that
For that aim, fix a function $\phi _0 \in C_{0,rad}^{\infty }( \mathbb {R}^N)$![]() such that $\phi _0 \neq 0$
such that $\phi _0 \neq 0$![]() and $\phi _0 \geq 0.$
and $\phi _0 \geq 0.$![]() By $(F_3),$
By $(F_3),$![]() we have
we have

We infer,

Hence, for $A > \frac {\frac {\left | \nabla \phi _0\right |_{L^N_{w_1}( \mathbb {R}^N)}^N}{N} + \frac {\left |\nabla \phi _0\right |_{L^q( \mathbb {R}^N)}^q}{q}}{\left |\phi _0\right |_{L^r( \mathbb {R}^N)}^r},$ the function $\gamma _0:[0,1] \rightarrow E_{q,1}$
the function $\gamma _0:[0,1] \rightarrow E_{q,1}$![]() defined by
defined by
belongs to $\Gamma.$![]() Consequently,
Consequently,

Clearly, there exists $A_0 > \frac {\frac {\left | \nabla \phi _0\right |_{L^N_{w_1}( \mathbb {R}^N)}^N}{N} + \frac {\left |\nabla \phi _0\right |_{L^q( \mathbb {R}^N)}^q}{q}}{\left |\phi _0\right |_{L^r( \mathbb {R}^N)}^r}$ large enough such that
large enough such that

This ends the proof of theorem 8.1.
Acknowledgements
The author is very grateful to the anonymous referee for his/her careful reading of the manuscript and his/her insightful and constructive remarks and comments that helped to clarify the content and improve the presentation of the results in this paper considerably.