Theoretical development

Reference RobinRobin (1955) solved the differential equation for steady conduction and advection of heat in the vertical, where the vertical velocity varies linearly from the negative of the net accumulation rate at the surface to zero at the base:

where k is the thermal diffusivity, Ȧ is the accumulation rate, θ is temperature, H is the thickness of the column, and y is a vertical coordinate with origin at the base of the column. With boundary conditions of a temperature at the upper surface, θ_H, and a temperature gradient β at the base of the column, the solution of Equation (1) is

where erf is the error function and

A previous generalization of Robin’s solution was given by Reference JonesJones (1978), who considered the steady-state solution in a flow plane with an additional assumption about the horizontal velocity profile. In the current study, we remain restricted to the vertical dimension, but abandon the steady-state assumption. For transient situations, the corresponding differential equation is

where t is time. Define the dimensionless coordinates

and use these to rewrite Equation (4).

The solution will be of the form

where θ_∞ is the final steady state given by Robin’s solution (Equation (2)) and satisfies Equation (6) with the initial conditions, at τ = 0,

Initial conditions will be non-zero if either θ_H, β, or Ȧ has shifted recently.

Since the surface temperatures and basal gradients are fixed by the steady-state solution, must satisfy the homogeneous boundary conditions,

where z* = αH, the dimensionless coordinate at the top of the column. Let

Then Ψ(Z, τ) satisfies

which is essentially Schrödinger’s equation for a parabolic potential well.

Separation of variables is achieved by considering the Sturm–Liouville eigenvalue problem,

Equation (12) has a complete set of orthonormal eigen-solutions, φ _n (z), with eigenvalues λ _n .

Any function that satisfies the boundary conditions (in particular ) can be expressed as a generalized Fourier series of the eigenfunctions,

Substituting Equation (13) into Equation (11), and noting that each φ _n satisfies Equation (12) with λ = λ _n , we see that c _n (τ) must satisfy

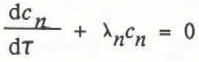
where at some time τ = τ’ c_n is related to θ by

allowing us to prescribe either initial values or a previous history of θ. All the eigenvalues, λ _n , are positive, so all the c _n have decaying solutions,

and in general Equation (11) is solved by

Solutions to Equation (12) can be constructed from

where M is the confluent hypergeometric function (also called Kummer function)

and where

(for example, Reference Slater, Abramowitz and StegunSlater, 1964). The even-power series is selected to satisfy the natural boundary condition, dΦ(0)/dy = 0. Eigenvalues, λ = λ _n , are found by solving

for the eigenvalues, λ _n .

Evaluation of the eigenvalues and eigenfunctions

The problem of finding eigenvalues and hence eigen-functions reduces to the problem of finding zeros of the confluent hypergeometric function by varying the numerator parameter. Such zeros may be found by Newton–Raphson iteration, using (Reference SlaterSlater, 1956):

Both the confluent hypergeometric function and its derivative are evaluated by summing the series. The signs on the parameters in Equation (18) force both series to have terms of alternating sign which simplifies convergence testing. For large n, λ _n and hence the numerator of each term of the series will be large. Therefore, many terms may be needed in the summation, and hence many digits in the computer calculation. Asymptotic expansions for large λ _n are hence useful.

The Newton–Raphson iteration requires an initial guess for the eigenvalue. We have developed an approximate formula for the eigenfunctions and eigenvalues by using a WKB approach, as described, for example, by Reference Matthews and WalkerMatthews and Walker (1970). Any linear, second-order differential equation can be converted to a form analogous to Equation (12), in which

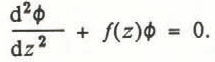
Working from the simple solutions that are available if f(z) is constant, the WKB method creates approximate solutions for cases in which f(z) is slowly varying. In this case, f(z) = λ − 1 − z ² is slowly varying if z*²/λ is small, in which case Equation (12) is approximately solved by

which satisfies the boundary conditions, and which leads to eigenvalues that satisfy

Equation (25) can be solved for λ _n , using the Newton–Raphson procedure for simplicity.

To establish an initial guess for the eigenvalues, we note that as z* gets large, the eigenfunctions are bounded only if the eigenvalues approach the values λ _n → 4n − 2 as can be shown from Reference Slater, Abramowitz and StegunSlater (1964, equation 13.5.1). The eigenfunctions are thus related to Hermite polynomials, as discussed below. The minimum value of the first eigenvalue is 2, which is used as an initial guess for λ ₁ in Equation (25). First estimates of higher eigenvalues are given by an approximate recursion relation, developed by assuming λ _n is large enough relative to z* that the second term of Equation (25) can be neglected,

In summary, the particular values of Ȧ and H for a given problem generate a value for z*. Taking an initial guess of λ ₁ = 2, we can improve the estimate by Newton–Raphson iteration of Equation (25) and use this estimate as an initial value for the Newton–Raphson iteration of Equation (21), in which the formula for the derivative with respect to the numerator parameter (Equation (22)) is essential. Subsequent eigenvalues are obtained by a similar procedure, except that the recursion formula (Equation (26)) is used to establish the initial guess.

The eigenvalues decrease as z* increases for a given eigenvalue number (Fig. 1; Table I). The first few eigenvalues approach the Hermite integer limit quite rapidly. The eigenfunctions appear as waves of varying period, with the number of zeros on the range [0, z*] being equal to the eigenfunction number, as illustrated in Figure 2 for z* = 2.0. As z* becomes large enough that eigenvalues approach their integer limits, the eigenfunctions become expressible in terms of Hermite polynomials, H _m (z), as

As with the eigenvalues, this limit is reached for the first few eigenfunctions at relatively small values of z* (Fig. 3).

Fig. 1. The value of the eigenvalue, λ_n, as a function of z* for the first four values of n.

Fig. 2. The first four eigenfunctions, φ_n(z,0), for a middle-range value of z* = 2.0.

Fig. 3. Examples of the first three eigenfunctions, showing function values for z* = 1 (solid curve), z* = 2 (long dashes), z* = 3 (alternating dashes), and the limiting eigenfunctions based on Hermite polynomials for z* → ∞ (short dashes).

The procedure described above gives accurate solutions using the confluent hypergeometric equation, but it also shows that the approximate WKB solution is accurate after the first few eigenfunctions, especially for small z*, and that Hermite polynomials may give adequate approximations to the first few eigenfunctions, especially for large z*. Any real ice sheet has a small accumulation rate at its center such that z* is likely less than 4. As z* approaches this limit, the accuracy of the direct method of calculating the eigenvalues becomes less certain, as the number of terms required for convergence of the confluent hypergeometric function becomes very large. At z* = 3.5, the maximum disagreement between the exact and the WKB eigenfunction is less than 1% by eigenfunction 9. For z* = 1, the maximum disagreement of the second eigenfunction between the exact and WKB solution is less than 10⁻⁴. The approximate eigenvalues correspondingly approach the real ones. Hence, for practical problems, only a few of the actual eigenvalues are needed and the simpler WKB formula may be used for the rest. In the solutions that are described below, we will generally be using such mixed series, in which the first few eigenfunctions are generated from the confluent hypergeometric function, and the remainder come from the approximate solution.

Responses to step-function perturbations

To illustrate the transient behavior of the solution in terms of conditions found in Nature, we show a few examples of idealized situations. In the first of these cases, we assume as initial conditions a profile that was in steady state prior to a 1° C increase in surface temperature at time zero. The transient solution thus predicts how the old steady-state temperature profile changes on its way to becoming a new steady state.

Assume the following values: H = 1000 m, Ȧ = 0.3 m/year, β = −0.02 ° C/m, and k = 36.2 m²/year. The value of z* is then 2.04. The initial departure from steady state will be −1°C throughout the column.

Two versions of the initial departure from steady state are calculated. First, the forcing at the surface at time zero is treated as a perfect step function. Fourier coefficients are fitted to this curve using a numerical integration over 800 equal intervals in the range [0, z*]. The series is truncated at 200 eigenfunctions, of which all but the first eight are the WKB approximation. Even at this number of eigenfunctions, the truncation leaves a visible oscillation in the initial conditions (Fig. 4). The oscillation becomes large near the surface discontinuity, as a manifestation of the Gibbs phenomenon (Reference Courant and HilbertCourant and Hilbert, 1966, chapter II, section 10.9). In the second case, the step-function forcing is applied as a linear variation over the top 100 m of the column, reflecting how a discretized numerical model with 100 m grid spacing would see the step-function change (Fig. 5). The transient responses to these initial conditions are shown in Figure 6.

Fig. 4. The initial departure from steady state for an instantaneous 1° C rise in surface temperature produced by a generalized Fourier series truncated at 200 eigenfunctions; z* is 2.04 in this example.

Fig. 5. Initial departure from steady state, as in Figure 3, except that the instantaneous" rise in surface temperature is now assumed to produce an instant linear variation over the top 10% of the column, as in a discrete grid of ten elements.

Fig. 6. Isochrones of the response to the initial conditions of Figures 4 and 5, given as departures from the final steady state. The isochrones are labeled with times in years following the application of the 1.0° C surface-temperature change. Solid isochrones are responses to the pure step-function change in boundary conditions (Fig. 4), while dashed isochrones are responses to the step-function change in boundary conditions as produced on a discretized grid (Fig. 5).

None of the noise in the Fourier series fit to the initial conditions remains in the transient solution 1 year later. For n = 200, the damping time is approximately 25 d. The discrete model increases the speed of penetration of the surface-temperature change into the ice, as is most clearly seen at 900 m height, at the base of the initial linear change. Small increases in penetration speed can be seen in these simulations down to 700 m height, but at all levels, including 900 m, the solution for a discretized step-function change becomes very similar to that for a pure step function after 500 years.

The effects of advection on the transient response are seen by comparing this response to the solution obtained for pure diffusion (Ȧ = 0). Figure 7 compares the responses to a pure step-function change in boundary conditions from the current solution and from a solution with Ȧ = 0. The isochrones at 30 years are virtually identical in the two cases. As the solution proceeds, the advective form progresses towards steady state more rapidly. In the later isochrones, the advective solution develops a characteristic upward concavity in the upper part of the column, which is not seen in the diffusive solution. To understand the change in importance of advection with time, we note that the Peclet number, Pe = ȦH/k, is 8.3 for the example in Figure 7, indicating that advection terms are dominant but not overwhelming. However, if we assign a Peclet number to each eigenfunction, in which the length scale is the wavelength of the eigenfunction rather than the total height of the column, we would have Pe << 1 for most of the eigenfunctions, so early in the time history of the solution when these higher eigenfunctions still have large Fourier coefficients, the solution is dominated by diffusion.

Fig. 7. Isochrones of the transient response, as in Figure 6, except that here the response to a pure step-function change using the value Ȧ = 0.3 (solid curves) is compared with the response to a step-function change under pure diffusion, Ȧ = 0 (dashed curves).

As a second example, we retain the height, diffusivity, and basal temperature gradient defined above, and subject a steady-state temperature profile to instantaneous changes in accumulation rate. For a constant surface temperature, increasing the value of Ȧ reduces the steady-state basal temperature. In these examples, we double the accumulation rate from 0.2 m/year to 0.4 m/year, so that the new steady-state temperature is 3° C colder at the base, and we halve the accumulation rate from 0.8 m/year to 0.4 m/year, so that the new steady state is 2.6 ° C warmer at the base (Fig. 8). The similarity in the size of the temperature difference produced by these different accumulation-rate changes results from the non-linearity of the influence of Ȧ on steady-state temperature, as shown in Equation (2). In these cases, simulating the initial departure from the final steady state required only six eigenfunctions to make the actual and simulated departures visually indistinguishable. Since the applied changes in accumulation produce a relatively smooth profile of initial departures from steady state, the diffusion processes are less important than the advective processes in producing the final solution for this case. Hence, the transient changes toward the new steady state, normalized by the initial departures, reflect a strong dependence on the first few eigenfunctions.

Fig. 8. Isochrones of the transient response, as in Figure 6, except that an instantaneous halving or doubling of the accumulation rate to a value of 0.4 m/year was applied to the column at time zero. In the solid curves, the column was initially in steady state with an accumulation rate of 0.2 m/year. In the dashed curves the column was initially in steady state with an accumulation rate of 0.8 m/year. The initial conditions (time 0) are included for each case.

These above examples implicitly assume that the vertical velocity profile adjusts instantly to the new mass balance. The velocity profile may be in instantaneous steady state with the surface profile of the ice sheet, but the surface profile is not likely to be in steady state with the mass-balance conditions. The assumption of instantaneous adjustment of vertical velocity therefore exaggerates the speed with which a mass-balance change affects the temperature profile.

To separate further the effects of diffusion and advection in the solution, we introduce two parameters: L is the wavelength of a perturbation in the temperature profile of a bore hole, as might for example be deduced from a Fourier analysis, and T is the response associated with a given wavelength, defined as the 1/e dissipation time. These may be defined for the nth eigenfunction as

The transient temperature solution implies a set of relationships among these two variables and the height and accumulation rate of the column. To obtain an approximate relation for the response time as a function of wavelength, we again assume λ is large enough that the second term of Equation (25) can be neglected, in which case Equation (28) implies

Observed scales can be inserted into Equation (29) and it can be inverted to make L, H, or Ȧ the dependent variable.

The combination of the exact solution and the WKB approximation can be used to plot the relationship between response time and perturbation wavelength for several combinations of height and rate (Fig. 9). These response-time versus wavelength curves were calculated using Equation (29) with small eigenvalues calculated from the exact solution and large eigenvalues calculated using Equation (25). Note that, for any given ice-sheet thickness H, the maximum wavelength is 4H. The thickness and accumulation rate only significantly affect the response time for wavelengths that are large compared to the thickness of the column, as implied by Equation (29). The ratio of Ȧ to 2H will always be on the order of 10⁻³ year⁻¹ for ice sheets. For all but the largest wavelengths, Equation (29) therefore reduces to

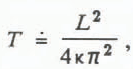
which is exactly the relation one would get for pure diffusion. In sum, the accumulation rate has an important effect on the response time only for wavelengths that are a significant fraction of the height of the column, while small-scale perturbations are almost entirely controlled by diffusion as further illustrated by Table II.

Fig. 9. Wavelength versus response time for an accumulation rate of 1 m/year and various column heights. Curves are for column heights of 100 m (solid), 300 m (long dashes), and 1000 m (short dashes), respectively.

Since z* is proportional to ȦH, we can see that the eigenvalues, which approach 4n − 2, become independent of the accumulation rate and height as the product of these quantities becomes large. Thus, by considering the lowest eigenvalue, we get an upper limit to the response time for an ice sheet, i.e.

which is half that inferred from Equation (28) for infinite wavelength. For the central part of East Antarctica, this implies a response time approaching 10⁵ years (data from Reference Budd, Budd, Jenssen and RadokBudd and others (1971)).

Deducing past climates in a real bore hole

To the extent that an ice-sheet vertical temperature profile satisfies the assumptions of the analytic model, the transient solution can be used to interpret bore-hole data in terms of the future and past history. If a temperature profile that is in steady state with current climate conditions is removed from an observed profile, the remainder presumably represents transient modes plus observational noise. By fitting one or more of the lower-order modes to this remainder, simple estimates can be made of the future decay of the departures from steady state. The modes can also be extrapolated backward in time to attempt to infer past history or initial disturbance. Such backward extrapolation requires care and gives information only in the largest vertical scales, since the higher-order modes not only may be more contaminated by noise but also may grow more rapidly with decreasing time.

As an example of backward extrapolation, we consider the temperature profile measured in 1979 in bore hole T020 on the south dome of Barnes Ice Cap. Of the several bore holes whose temperature profiles were analyzed and discussed by Reference Hooke, Hooke, Alexander and GustafsonHooke and others (1980), this one is most firmly in the accumulation area of the ice cap and hence suitable for analysis by the current solution. Reference Hooke, Hooke, Alexander and GustafsonHooke and others (1980) used a numerical model to reconstruct a climate scenario that could have led to the current temperature field in bore hole T020. Their model included vertical advection and diffusion, as does our Equation (4), with the additional processes of strain heating and horizontal advection. The horizontal temperature gradient was held constant with height, but the horizontal velocity profile varied with depth according to the steady-state solution of Reference NyeNye (1952). Additionally, the vertical velocity decreased from the surface in their model proportionally to the decrease in horizontal velocity. They concluded that the temperature distribution in bore hole T020 could have been caused by a 2.5° C cooling in the decade of the 1940s, followed by a 1.0° C warming in 1969.

Analysis of the temperature profile is based on the fact that the lower part of the measured profile is well represented by a steady-state solution whose parameters are θ_H = −8.35°C, Ȧ = 0.32 m/year, and β = −0.0175°C/m (Fig. 10). These numbers closely match those of Reference Hooke, Hooke, Alexander and GustafsonHooke and others (1980) except for β, which is of greater magnitude in the current case, probably because the current solution does not include strain heating. If the ice-temperature profile was indeed in steady state with these conditions at some time in the past, the deviations from that steady state in the current profile suggest that the bore hole is responding to a large cooling which has since partly reversed. If we assume that a column has responded to two step-function changes in surface temperature, the Fourier coefficients at a time τ after the last change can be expressed as

where c ^* _k are the Fourier coefficients that would result from a unit step-function increase in surface temperature, Δθ is the initial change in temperature, ƞ is the fraction of ∆θ by which the temperature changed back at the second change, and Δτ is the time between the two surface-temperature changes. Matching this solution to an observed pattern of temperature deviations requires that we estimate three parameters; τ, ∆τ, and ∆θ, with η being a direct function of ∆θ and the observed difference between the current surface temperature and the temperature with which the lower part of the bore hole is in steady state. These parameters are determined by minimizing a weighted difference between the two kinds of Fourier coefficients,

where N is a truncation value, chosen here to be 12. For the current case, the values ∆θ = −2.6˚ C and η = 0.49 for changes preceding the measurement by 35 and 8.1 years, respectively, produce a good match with the observed data (Fig. 11).

Fig. 10. Comparison of the observed temperature profile in bore hole T020 of Barnes Ice Cap in 1979 (dashed curve) with a steady-state temperature profile for θ_H = −8.35^°C, Ȧ = 0.32 m/year, and β = −0.0175° C/m (solid curve). The total depth of ice at the bore hole is 369 m, in which the actual measurements extend downward to 91 m above the bed.

Fig. 11. Comparison of the observed departure from a steady state with the 1979 surface temperature in bore hole T020 (solid curve) and the departure from steady state produced by assuming a step-function decrease in surface temperature of 2.6° C in 1944 followed by a rise of 1.3° C in 1971 (dashed curve).

These calculations show what can be done with the analytic solution using real bore-hole data. They support the results from the numerical model of Reference Hooke, Hooke, Alexander and GustafsonHooke and others (1980). Our backwards extrapolation is insensitive to the smallest temperature variations near the surface of the bore hole, as small temperature variations deeper in the bore hole have as great an effect on the Fourier coefficients. Had it been necessary to assume variations in Ȧ or β, the backwards extrapolation would have been more awkward. For real bore-hole studies, the solution provides an economical, automatic means of obtaining first guesses for the climate changes. The few tunable parameters allow for simple exploratory analysis of a bore-hole temperature profile. Had the sequence of studies been different, Hooke and others might have found our solution useful for limiting the range of possibilities needed for consideration in their more general numerical model. For the analysis of a real bore-hole profile, a more general treatment may be needed to allow vertical velocity variations other than the linear variation and to include the effects of horizontal advection.

A finite-difference analogue for general strain-rates

Our inference of response times in terms of the lowest eigenvalue can be generalized using the finite-difference or finite-element analogue of our differential equation. For example, we assume a vertical velocity profile given by

where k ≥ 1. Examples of such vertical velocity profiles are shown in Figure 12, where Ȧ and H are as used for bore hole T020. The first eigenvalue of the solution for any of these velocity profiles can be accurately approximated by the first eigenvalue of the matrix of a finite-difference solution. In this case, the grid spacing is 1 m, which is the actual spacing of the original measurements, and the simplest second-order difference approximation, Ψ _i″ = (Ψ _i−1 + Ψ _i+1 − 2Ψ _i)/h ², is used to develop the matrix. The case k = 1 reproduces the theoretical eigenvalue, 2.7, and increasing k leads to increases in the eigenvalue, and hence decreases in response time (Fig. 13), confirming the qualitative expectation that the greater downward velocities shown in Figure 12 should lead to faster responses. The limit k → ∞ produces a simpler differential equation whose solution provides direct expressions for the eigenvalues, but this is not especially useful, as this limit is approached neither rapidly nor monotonically.

Fig. 12. Vertical velocity profiles produced by Equation (33) for values of k = 1, 2, 3, and 4, using Ȧ = 0.32 m/year and H = 369 m.

Fig. 13. Values of the first eigenvalue versus the exponent k of Equation (33), calculated as matrix eigenvalues using second-order finite differences.