1. Introduction
The flow of polar ice masses plays an essential part in climate simulations, i.e. past climate history, at least to some extent stored in ice particles, is expected to be reconstructable by analyzing ice cores (e.g.Reference Thorsteinsson, Kipfstuhl and MillerThorsteinsson and others, 1997). The impact of the actual orientation distribution of c axes (texture) on thermomechanical (flow) properties is evident from laboratory and field data (e.g. Reference Bouchez and DuvalBouchez and Duval, 1982; Reference Budd and JackaBudd and Jacka, 1989). Ice crystals possess hexagonal symmetry with three glide planes (basal, prismatic and pyramidal) where creep deformation occurs mainly along the basal plane, represented by its c axis (Reference Bouchez and DuvalBouchez and Duval, 1982). Several authors have developed constitutive models for (strain-)induced anisotropy capable of taking texture changes into account (e.g.Reference Van der Veen and WhillansVan der Veen and Whillans, 1994;)
Reference Castelnau, Thorsteinsson, Kipfstuhl, Duval and CanovaCastelnau and others, 1996). The common idea is: based on knowledge of the behaviour of crystallites (mesoscale), the macro-scale behaviour is derived via homogenization. However, since the model is to be used for large-scale flow simulations the numerical effort should be as small as possible.
This problem was recently addressed when fabric evolution was considered using tensor-valued internal variables (e.g. Reference Morland and StaroszczykMorland and Staroszczyk, 1998). In contrast to this approach, where the number of fields is increased, Reference Gagliardini, Meyssonnier, Hutter, Wang and BeerGagliardini and Meyssonnier (1999) and Reference Go«dert and HutterGödert and Hutter (2000) increased the number of field quantities. To this end, the classical space, ![]() is extended to
is extended to ![]() where n = 2,3 and d = 1, 2. d denotes the dimension of the unit sphere Sd. This implies that the position of a grain as well as its size and shape are considered unimportant. Consequently, there remains the orientation of a grain, here expressed by n : Sd. x indicates the macroscopic position of a material point. Direct numerical analysis with respect to the mesoscopic space, V would require too much effort, so the meso-approach implies the statistical concept of orientation distribution function (ODF), where the ODF,
where n = 2,3 and d = 1, 2. d denotes the dimension of the unit sphere Sd. This implies that the position of a grain as well as its size and shape are considered unimportant. Consequently, there remains the orientation of a grain, here expressed by n : Sd. x indicates the macroscopic position of a material point. Direct numerical analysis with respect to the mesoscopic space, V would require too much effort, so the meso-approach implies the statistical concept of orientation distribution function (ODF), where the ODF, ![]() may be interpreted as a probability density fulfilling
may be interpreted as a probability density fulfilling

Equation (1) already suggests the rule yielding macroscopic quantities, ![]() from those defined on the mesoscopic scale,
from those defined on the mesoscopic scale, ![]()

The above considerations can be derived more descriptively if one assumes a volume of influence, v, around each material point x of the continuum. Considering that the deformation is incompressible, macroscopic entities can be obtained simply by volume averaging. Then f is given as the volume fraction of vn and v, where vn represents the volume of equally oriented crystallites within v, so that vf = vn. Note that all quantities associated with the grain level are denoted by the subindex ()n, whereas, if it seems necessary to prevent misunderstandings, the macroscopic or polycrystal level is indicated by ()a (see Appendix C for further explanation of the underlying notation). Applying Equation (2) to the mesoscopic structure, one obtains the associated macroscopic structure tensors as
2. Kinematics
Ice single crystallites are treated as “rigidly elastic” viscous material. In general, for hexagonal crystals the contribution of pyramidal slip can be neglected. Furthermore, reorientation of the c axes is then governed solely by basal slip, so that, since we are interested in the evolution of the c axes, for the sake of conciseness we may restrict the following to basal slip only. Then decomposition of the deformation gradient into an “elastic” rotation, Rn , and an inelastic deformation, ![]() leads to
leads to
the mesoscopic deformation and its associated velocity gradient, respectively. Here, the overdot indicates time differentiation, and γ and eγ denote the amount of basal slip and its direction, respectively. Here, D n = sym(Ln) denotes the stretching, and W n = skw(Ln) the spin. Further additive decomposition of the total grain spin W n into its elastic and inelastic contributions,
may be obtained by straightforward calculation, whereas stretching is completely inelastic, ![]() Due to the inextensibility of c axes, their evolution is given via the “elastic”spin, (e.g. Reference DafaliasDafalias, 1984), yielding
Due to the inextensibility of c axes, their evolution is given via the “elastic”spin, (e.g. Reference DafaliasDafalias, 1984), yielding
where the inelastic spin, ![]() can be expressed in terms of the inelastic mesoscale stretching, D n ,
can be expressed in terms of the inelastic mesoscale stretching, D n ,
3. Balance Equations
Let z = x + n describe a point of ![]() an open domain of the extended space V where
an open domain of the extended space V where![]() and n : Ωn
C Sd, with n≥d,n ϵ {2, 3} and d ϵ {1, 2}. If Ψ denotes the density of a physical quantity, it globally changes its value through production and external supply, π Ψ , as well as by flux, q Ψ . Straightforward generalization of Reynolds’ transport theorem gives
and n : Ωn
C Sd, with n≥d,n ϵ {2, 3} and d ϵ {1, 2}. If Ψ denotes the density of a physical quantity, it globally changes its value through production and external supply, π Ψ , as well as by flux, q Ψ . Straightforward generalization of Reynolds’ transport theorem gives

where the gradient, ▽z = ▽x + ▽n , as well as velocity, v z = v x + v n , and flux, q Ψ = q Ψx + q Ψn , can be decomposed, leading to the generalized balance
Without considering the details, the (pure mechanical) problem will be reduced to a set of balance equations consisting of the macroscopic balances of mass, momentum and angular momentum supplemented by the mesoscopic balance of orientation (Equation (10)). From Equation (9), the mass balance is obtained if the mesoscopic mass density Ψ = vn = vf is substituted. Independency of f and v then requires the macroscopic mass balance, ∂tv + ▽ x • (v xv) = 0, as well as the mesoscopic mass balance,
which describes the evolution of the orientation distribution. Supplemented by an appropriate initial condition, Equation (10) can be solved for f if v n and q v n are given.
4. Constitutive Assumptions
The constitutive equations are formulated in two steps. First the behaviour of an isolated crystallite is described as a function of the set of macroscopic variables, S = { X , A } , where X = X T represents a generalized external driving force. In a second step, the interaction of the single crystallites within their polycrystalline environment is taken into account. Let ![]() and Ψ n denote an additive quantity of an isolated and an embedded crystallite, respectively, then a consistent description is defined by
and Ψ n denote an additive quantity of an isolated and an embedded crystallite, respectively, then a consistent description is defined by
where α Ψ represents a function of macroscopic variables only (e.g. Reference Go«dert, Hutter, Wang and BeerGödert, 1999). The limit cases of a random and a completely aligned c-axes distribution are governed by α Ψ → 0 and α Ψ → 1, respectively. Note that, due to ![]() consistency is fulfilled by construction, i. e. the macroscopic behaviour of the material is invariant with respect to the αΨ modification. That is, a material quantity is properly defined by αΨ and
consistency is fulfilled by construction, i. e. the macroscopic behaviour of the material is invariant with respect to the αΨ modification. That is, a material quantity is properly defined by αΨ and ![]()
The set of mesoscopic variables to be determined via constitutive assumptions then comprises the total spin ![]() the stretching
the stretching ![]() as well as the Cauchy stress the orientation flux vector
as well as the Cauchy stress the orientation flux vector ![]() and in the second step the corresponding weighting coefficients αW, αD, αT
and αq, respectively.
and in the second step the corresponding weighting coefficients αW, αD, αT
and αq, respectively.
4.1. Isolated single crystal
Intracrystalline slip
Due to the lack of five independent slip systems the Sachs– Reuss or static assumption is adopted. Furthermore the Voigt–Taylor assumption is applied for the spin, yielding
According to related work, slip is assumed to be well approximated by Newtonian creep. Anisotropy of the single crystal is determined by its c axis, yielding a transversely isotropic material behaviour compactly written as
where ![]()
−N, and μ denotes the basal fluidity. This form is equivalent to the expression proposed by Reference Gagliardini, Meyssonnier, Hutter, Wang and BeerGagliardini and Meyssonnier (1999), but in practice the grain anisotropy parameter β ≪ 1.
Rotation recrystallization (polygonization)
Rotation recrystallization or polygonization is generally associated with the formation of (sub)grain boundaries due to heterogeneous loading. This fragmentation process mainly affects grains that are not well oriented for dislocation glide, so-called “hard grains”. Since fragmentation is accompanied by specific reorientation of certain lattice portions, the resulting subgrains tend to be softer than their parent grains (e.g. Reference PoirierPoirier, 1985). From a mathematical point of view, orientation moves from hard to soft configurations. There is a similarity between heat flux and what we call orientation flux. Analogous to heat-flux problems, rotation recrystallization can be considered as a diffusive flux of orientation described via Fick’s law with respect to the hardness, qvn = −λ n▽n (Hn). On the other hand, considering that, for each orientation, only a certain fraction of grains polygonizes, fragmentation may also be understood in the sense of Brownian motion. Hardness, λHHn > 0, represents then an external loading and can therefore be expected as a general function of N and X, where λH ≥ 0 is assumed to depend on macroscopic quantities only. Yet experience tells us that direct (normal) loading with respect to the basal plane is most important, so the set of independent variables can be reduced to the invariants INX i = (N ; Xi) (i = 1, 2, 3). Furthermore, restricting non-linearity of Hn to quadratic order, it is supposed to be appropriately represented by

where the coefficients hi are isotropic functions of the set S.
Grain boundary migration
If grain growth takes place, nearest neighbours are always involved. Therefore, grain growth is in general "intra-orientational”, not describable by diffusion-type evolutionary terms (but rather by an appropriate production term). Reference Montagnat and DuvalMontagnat and Duval (2000) developed a model for the dislocation balance at the low-velocity regime of grain boundary migration, which is essentially based on the hypothesis that grain boundary migration and polygonization are concurrent processes (Reference Montagnat and DuvalMontagnat and Duval, 2000). Subgrains created by polygonization are supposed to merge again, so that the (mean) orientation of the grain remains the same during this circular process. However, neither the orientation of subgrains nor that of neighbouring grains was explicitly taken into account. It seems to be a reasonable working hypothesis that a grain grows at the expense of its neighbours, whatever its orientation. Grain boundary migration, at least in the low-velocity regime, can then be modelled by an evolutionary term similar to that derived for rotation recrystallization, but acting in the “opposite direction”.
4.2. Embedded single crystal
Considering Equations (12), the coefficients αW and αT are already defined. αD can be motivated by alternative (second-order) kinematically compatible deformation mechanisms like dislocation climb and rotation recrystallization, yielding
where αD
is a monotonic function of the degree of alignment, αP, defined below. Recalling that αD
→ 1 for completely aligned c axes, a distinction between meso- and macro-scale becomes obsolete, leading to the consistent result Dn = D. Furthermore, the physically obligatory energy-consistency condition T • • D = (Tn • • Dn) is fulfilled. The hardness of an embedded grain is formally given by Hn = αHHa + (1 - αH)
![]() where αH
again denotes a function of the degree of c-axes alignment. However, considering that instead of the hardness its gradient,
where αH
again denotes a function of the degree of c-axes alignment. However, considering that instead of the hardness its gradient, ![]() represents the constitutive quantity, the term H a
becomes meaningless. Then the orientation flux is given by
represents the constitutive quantity, the term H a
becomes meaningless. Then the orientation flux is given by
(λn comprises (1 - αH)). In order to describe the intensity of the orientation flux, we suggest that the misorientation angle between polygonized grains depends linearly on the number of dislocations suggesting λn ≈ ndλa. Assuming further the same dislocation density pd for all equal orientated grains, one may conclude from nd = ρdvn ≈ f the relocation
Rotation recrystallization (as well as grain boundary migration) then becomes describable via
4.3. Homogenization
Macroscopic quantities are obtained by applying Equation (2), yielding identities for the stress and the spin. Recalling the invariance of the α modification with respect to the macroscopic behaviour, the strain-rate tensor is given as
Hence, Equation (19) is completely determined if the temporal evolution of the fourth-order structure tensor A is known. Referring to related work, the following considerations will be restricted to orthotropic material behaviour, i.e. to the evolution of the second-order tensor. Taking the mesoscopic mass balance (Equation (10)) into account, the local change of the structure is given as
Applying Equations (6), (7) and (15) and considering 2Pn ••Pn = Pn; the Jaumann rate A = ∂t A - 2sym(WA) takes the form
Making use of Equations (19), (17) and (18) with ![]() and application of Gauss theorem (on the unit sphere (e.g. Appendices A and B)), the co-rotational evolution of A (Equation (21)) takes the form
and application of Gauss theorem (on the unit sphere (e.g. Appendices A and B)), the co-rotational evolution of A (Equation (21)) takes the form

4.4. Closure approximation
The mean projection operator, Pa, contains the fourth-order structure tensor, so the second-order evolution equation (21) is not closed. The same argument holds for the fourth-order evolution equation; here the sixth-order structure tensor is needed. Generally the evolution of the 2nth moment necessitates the 2(n+1)th moment, resulting in an infinite hierarchy of equations. Since we restricted considerations to orthotropic material behaviour, it suffices to describe the evolution of the second-order structure tensor. Hence, an appropriate expression for A is needed. To this end, Reference Gagliardini, Meyssonnier, Hutter, Wang and BeerGagliardini and Meyssonnier (1999) and Reference Go«dert and HutterGödert and Hutter (2000) restricted the ODF
by certain symmetry conditions (to orthotropy), so that explicit computation of A becomes feasible under plane flow conditions. I n contrast to those restrictions, we use a closure approximation, so the model is not restricted to plane flow. Recalling that c-axes rearrangement takes place monotonically in the sense that fabric develops continuously from randomly distributed c axes at the top of an ice sheet to more-or-less completely aligned c axes at its bottom, an appropriate approximation of the fourth-order terms must bridge the gap between the two extremal distributions. In accordance with Reference Advani and TuckerAdvani and Tucker (1987), this is achieved by approximating Pa by the so-called hybrid closure

where
and
denotes the degree of alignment for the case n = 3 and d = 2.
5. Application
To carry out a completely coupled analysis, Equation (22) is to be substituted into
Alternatively with a view to efficient numerical considerations, the local time derivative can be split into a material and a spatial part, ∂t () = ∂τ1() + ∂τ2(), yielding
Accordingly the evolution of A is decoupled into a pure material and spatial part (e.g. Equations (26)a and (26)b). The constitutive model is then completely given by Equations (19), (22) and (26) or (25). It will be shown that besides the non-diffusive, i.e. qvn = 0, static models of Reference Gagliardini, Meyssonnier, Hutter, Wang and BeerGagliardini and Meyssonnier (1999), i.e. αD = 0, and Reference Go«dert, Hutter, Wang and BeerGödert (1999), i.e. β = 0, the diffusive model of Reference Staroszczyk and MorlandStaroszczyk and Morland (2001) can also to some extent be treated as a special case within the presented approach.
In the following, several special cases will be taken into account for the material part of Equation (26). First, uniaxial, compressive loading is considered. Here a single-maximum fabric develops along the loading axis, which at the same time represents the direction of maximum hardness. Hn may therefore be qualitatively identified with the ODF. Applying qvn = - λA ▽n(f) , with λA = const., the second righthand term of Equation (21) takes the form
The local evolution of the structure tensor is then given as
In general, λ A is a function of the ODF (e.g. Equation (17)), so the resulting relaxation (Equation (27)) is more likely related to dynamic recrystallization (rapid grain boundary) than to the deletion of preferably orientated subgrain boundaries.
General loading
For the sake of simplicity, we assume /3 = 0 for the evolution equation. Furthermore, the diffusive term is restricted to depend linearly on the loading, but remains invariant under a change in loading direction. These requirements are met if i = 2 and ![]() yielding
yielding
where, with ![]() the co-rotational evolution can be written as
the co-rotational evolution can be written as
Non-diffusive, coaxial loading
First, we consider pure mechanical texture evolution, i.e. λA = 0. Then due to coaxial loading, i.e. W = 0, Equation (26) a reduces to
if the above model is restricted to basal glide only, that is αD = 0 as well as β = 0. Integration of Equation (31), A = A 0 + / A dt, carried out via exponential mapping of the actual deformation gradient, Fk =
exp(Lkδt)Fk–1,
reveals that the second-order structure tensor A can be replaced by the Cauchy–Green tensor B recursively defined by ![]() so that, if B0 = I, one obtains the relation
so that, if B0 = I, one obtains the relation

Starting from a random c-axes distribution, ![]() the actual structure tensor is given by
the actual structure tensor is given by
where H represents the Hencky strain tensor. Although this holds true only for path-independent problems, one might be in favour of taking H or equivalently B as the general macroscopic structural variable. With this in mind and in order to accomplish the evolution equation, the spatial part (Equation (26) b) can be written in terms of the deformation gradient, F, so that further mesoscopic considerations become obsolete:
In principle, this is what Reference Morland and StaroszczykMorland and Staroszczyk (1998) proposed ad hoc, when they assumed the deviatoric stress to be an isotropic function of the eigenvectors and eigenvalues of B. Reference Staroszczyk and MorlandStaroszczyk and Morland (2001) extended their model to migration recrystallization by adding a term proportional to (I - 3B), which also agrees with our perceptions, if A is replaced by B in Equation (27). This shows that, with respect to the evolution of the internal structure, their model is closely related to the proposed static, single-slip model (i.e. basal glide only), with αD = 0, β = 0.
Simple shear
In order to assess the capabilities of the model, a simple shear deformation, D = κ sym(e1 ⊗ e2), is taken into account. Two parameter variations of the evolution equation are considered, whereas the stress–strain-rate relation for both cases is based on β = 0.25 and α = 1.2, where the interaction parameter α, defined via
is determined from comparison with field data (e.g. Reference Go«dert, Hutter, Wang and BeerGödert, 1999). The grain anisotropy parameter β = 0.25 is taken from Reference Gagliardini, Meyssonnier, Hutter, Wang and BeerGagliardini and Meyssonnier (1999) as a reasonable choice in view of the resulting c-axes distribution. First, diffusive as well as grain interaction processes are neglected completely, i.e. Hn = const. and α = 0, respectively. Hence, (double slip) model A coincides with the constitutive equations of Reference Gagliardini, Meyssonnier, Hutter, Wang and BeerGagliardini and Meyssonnier (1999). Model B (single slip), the second variation, is chosen in accordance with Reference Go«dert, Hutter, Wang and BeerGödert (1999), i.e. α =1.2.
Model A (Fig. 1a): α = 0:0; β = 0:25;

Fig. 1. Evolution of the normalized shear, uniaxial- and biaxial-compressive fluidities (μshear, μuniaxial, μbiaxial ) due to normalized simple shear deformation: (a) model A (α = 0:0, β = 0:25); (b) model B (α =1.2, β = 0.0).
Model B (Fig. 1b): α = 1:2; β = 0:0;
Diffusive effects, representing the wide range of possible material responses, are principally reflected in Figure 2 denoting the fluidities if rearrangement of the orientations occurs due to rotation recrystallization. In accordance with the above considerations, diffusion is implemented via Equations (27) and (30), in the following called λA- and λB-type diffusion, respectively. As one would expect, λ A = const. can be used to adjust the value of the maximum alignment (not plotted here). In contrast, λB-type diffusion leads to an oscillation of the fluidities (e.g. Fig. 2a). In order to obtain an oscillating behaviour also for λA-type diffusion, λ A is to be controlled by the degree of alignment, αP. That is, starting with λA = 0, then if αP exceeds a threshold value, the setting λ A ≠ 0 leads to a weakening of the actual alignment until αP falls below a certain value affecting λ A = 0, so that the process may start again (e.g. Fig. 2b).

Fig. 2. Same as Figure 1, but with model A(α = 0:0, β = 0:25) plus λA-type (a) and λB-type diffusion (b) controlled through the degree of alignment, αP.
6. Summary
The pure mechanical part of the model is essentially controlled by two parameters, α and β. Correspondingly three variations of the evolution equation are considered: (A) α = 0, β = 0 (single slip); (B) α ≠ 0, β = 0 (grain interaction); (C) α = 0,β ≠0 (double slip). For model A it can be shown that under simple shear deformation the ODF develops a single maximum along the maximum eigenvalue of D. As a result, the material reflects hardening behaviour in contradiction to experimental evidence. On the other hand, assuming deformation path independency, it was shown that the structure tensor may be identified with the Cauchy–Green tensor B. This corresponds to the ideas published by Reference Morland and StaroszczykMorland and Staroszczyk (1998) and Reference Staroszczyk and MorlandStaroszczyk and Morland (2001). As was shown in earlier work, the interaction parameter α (model B) is active solely for the strain field within a grain, i.e. it vanishes via homogenization. Consequently the stress relations for models A and B are macroscopically identical. Figures 1 and 2 show that the model is capable of reproducing essential features at least qualitatively. That is, one may observe an increasing shear fluidity due to an increasing c-axes alignment perpendicular to the shear direction. However, comparison with experiments (Reference Budd and JackaBudd and Jacka, 1989; Reference Jacka, Jun and HondohJacka and Li, 2000) reveals that softening induced solely by the texture development does not meet quantitative requirements, so an additional softening (enhancement factor) must be considered.
Originally motivated by the need for a numerically more efficient theory, especially if one is concerned with fully three-dimensional problems, the proposed constitutive equations represent a combination of a classical approach based essentially on representation theorems and an ODF-based mesoscopic theory. The implementation of the proposed structure tensor-based model into a fully coupled finite-element scheme will be discussed elsewhere.
Appendix A

Here, o ϵ { • , x , ⊗ } is used as a general product operator.
Appendix B

Appendix C
First-order tensors (vectors) are denoted by small letters, t, and second-order tensors by capital letters T. Tensors of arbitrary order are given through ![]() where
where 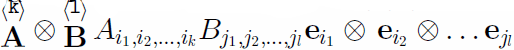 represents the tensor product. Transposition is given through
represents the tensor product. Transposition is given through  The inner product of tensors of equal order is defined via contraction
The inner product of tensors of equal order is defined via contraction 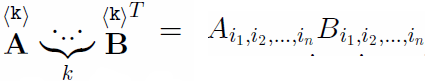 Ai1,i2,...,in Bi1,i2,...,in, so an inner product of two second-order tensors is given by their two-fold contraction (A; B) = A • • BT , also compactly written as the first invariant IAB of the tensor A • B. Second-order tensors may be uniquely decomposed into a symmetric, sym
Ai1,i2,...,in Bi1,i2,...,in, so an inner product of two second-order tensors is given by their two-fold contraction (A; B) = A • • BT , also compactly written as the first invariant IAB of the tensor A • B. Second-order tensors may be uniquely decomposed into a symmetric, sym ![]() and an asymmetric part, skw
and an asymmetric part, skw![]() A] = 1 A Anticipating further the need for generalized higher-order orientation tensors, the recursive, formula for the mesoscopic structure tensors,
A] = 1 A Anticipating further the need for generalized higher-order orientation tensors, the recursive, formula for the mesoscopic structure tensors, ![]() where
where ![]() is to be established, where n = sin Θ cosφ e 1 + sin Θ sinφ e 2 + cos Θ e . Alternative notation of fourth-order tensors is given as
is to be established, where n = sin Θ cosφ e 1 + sin Θ sinφ e 2 + cos Θ e . Alternative notation of fourth-order tensors is given as ![]() and I dev = Isym - I ⊗ I , representing the fourth-order structure tensor, the identities on the space of symmetric and symmetric deviatoric tensors, respectively.
and I dev = Isym - I ⊗ I , representing the fourth-order structure tensor, the identities on the space of symmetric and symmetric deviatoric tensors, respectively.






