1. Introduction
Swept wings are widely employed in commercial and military aircraft, due to their beneficial characteristics in high-speed flight. However, the associated sweep angle ultimately results in a three-dimensional boundary layer developing on the wing surface. A swept-wing boundary layer is characterised by a cross-flow (CF) component due to the known imbalance between centripetal and pressure forces (Saric, Reed & White Reference Saric, Reed and White2003). The CF component is perpendicular to the outer inviscid streamline and exhibits an inflection point in the velocity profile, giving rise to CF instabilities (CFIs). In a favourable pressure gradient region, CFIs are destabilised and ultimately determine the laminar–turbulent transition process. Bippes (Reference Bippes1999) concludes that primary stationary and travelling CFIs are initiated and amplified depending on distinct environmental conditions. In realistic flight conditions (i.e. characterised by low free-stream turbulence intensity ![]() $T_u$), the swept-wing boundary layer is dominated by stationary CFIs which are mainly conditioned by surface roughness. Instead, travelling CFIs are favoured by high
$T_u$), the swept-wing boundary layer is dominated by stationary CFIs which are mainly conditioned by surface roughness. Instead, travelling CFIs are favoured by high ![]() $T_u$. During the development of these instabilities, primary stationary or travelling CF vortices generate localised high-shear regions in the boundary layer, which in turn induce strong secondary instabilities that lead to rapid transition to turbulence (Guo & Kloker Reference Guo and Kloker2019). In-depth and thorough reviews of receptivity, growth and dynamics of CFIs and associated transition process can be found in Bippes (Reference Bippes1999), Saric et al. (Reference Saric, Reed and White2003) and Malik et al. (Reference Malik, Li, Choudhari and Chang1999). Given the critical role of CFIs in swept-wing boundary layer transition, direct or indirect reduction of their amplitude can be expected to delay transition and prolong laminar flow, thus reducing aerodynamic drag.
$T_u$. During the development of these instabilities, primary stationary or travelling CF vortices generate localised high-shear regions in the boundary layer, which in turn induce strong secondary instabilities that lead to rapid transition to turbulence (Guo & Kloker Reference Guo and Kloker2019). In-depth and thorough reviews of receptivity, growth and dynamics of CFIs and associated transition process can be found in Bippes (Reference Bippes1999), Saric et al. (Reference Saric, Reed and White2003) and Malik et al. (Reference Malik, Li, Choudhari and Chang1999). Given the critical role of CFIs in swept-wing boundary layer transition, direct or indirect reduction of their amplitude can be expected to delay transition and prolong laminar flow, thus reducing aerodynamic drag.
A promising technique to achieve this goal is the so-called laminar flow control (LFC). In this work, the definition of LFC is intentionally kept broad, thus entailing any passive or active flow control device close to the wing leading edge, with the potential to maintain laminar flow over aerodynamic bodies by delaying transition. A review of early experiments and flight-tests of LFC is given by Joslin (Reference Joslin1998), along with a more recent review by Krishnan, Bertram & Seibel (Reference Krishnan, Bertram and Seibel2017). Significant advancements in LFC on swept wings have been made in recent decades, such as the passive discrete roughness element (DRE) method (Saric, Carrillo & Reibert Reference Saric, Carrillo and Reibert1998), pinpoint suction (Friederich & Kloker Reference Friederich and Kloker2012) and upstream flow deformation (UFD) suction or suction through slots (Messing & Kloker Reference Messing and Kloker2010). Despite the similar objective of transition delay achieved by the aforementioned methods, the fundamental working principles behind them vary significantly. In brief, the DRE/UFD methods use carefully positioned forcing units towards enhancing subcritical stationary CFI modes. Through nonlinear interactions, the latter suppress critical stationary CFI modes, thus delaying transition. In contrast, pinpoint suction locally modulates and attenuates the existing stationary CFI, while suction through slots directly reduces the boundary layer CF component to delay transition. Despite the proven effectiveness of the mechanisms behind these methods, it should be noted that the control devices utilised (to implement these mechanisms) do show distinct drawbacks. For instance, as a passive technique, DRE-based LFC is expected to work only in specific flight conditions and can be less effective or even detrimental in off-design conditions. In contrast, the suction-based LFC is sufficiently robust to changing conditions, but underlines a highly interdisciplinary strategy. Specifically, the corresponding suction system is typically complex (e.g. piping, compressor and valves) and brings additional demands of geometry and manufacturing (e.g. hole quality, system weight and volume), challenging the design and practicality of suction-based LFC.
In summary, the aforementioned methods reveal the potential of LFC for swept-wing transition control. Nonetheless, the performance and practicality of LFC can be significantly improved by deploying alternative active control devices, which ought to be simpler and more robust.
1.1. Plasma-based LFC strategies on swept wings
In recent years, the dielectric barrier discharge (DBD) plasma actuator (PA) has received considerable attentions as a potential enabler of LFC applications. This active flow control device presents various features which can be beneficial for transition delay applications, such as the ability to be flush-mounted on aerodynamic surfaces, extremely fast response due to purely electrical operation and high robustness due to lack of mechanically driven parts (Corke, Enloe & Wilkinson Reference Corke, Enloe and Wilkinson2010; Benard & Moreau Reference Benard and Moreau2014; Kotsonis Reference Kotsonis2015). These advantages make a PA a potential candidate device to implement some of the aforementioned LFC methods. Generally, the plasma-based LFC utilises the volume-distributed body force produced by the plasma. Excellent reviews on the physics and scaling of body force production are given in Corke et al. (Reference Corke, Enloe and Wilkinson2010) and Benard & Moreau (Reference Benard and Moreau2014). However, most of plasma-related studies and flow control applications have focused on two-dimensional boundary layers as found, for example, in Grundmann & Tropea (Reference Grundmann and Tropea2008). The attempts and studies of plasma-based LFC for CF-dominated boundary layers have started more recently. Until now, several strategies of plasma-based LFC have been proposed targeting swept-wing boundary layers and are summarised below.
(i) UFD strategy. This method directly follows the principle of aforementioned passive DRE-based LFC and UFD suction techniques. By exciting subcritical CFI modes, the growth of critical CFI modes is suppressed through nonlinear interactions, thereby achieving transition delay. The first experimental investigation was reported by Schuele, Corke & Matlis (Reference Schuele, Corke and Matlis2013) where stationary CFI modes were successfully excited by micrometric-sized PAs on a right-circular cone operating at Mach 3.5. A similar approach was followed by Serpieri, Venkata & Kotsonis (Reference Serpieri, Venkata and Kotsonis2017) where various stationary CFI modes were conditioned on a swept-wing model using PAs. Nonetheless, the efficacy of the plasma-based UFD strategy is mainly demonstrated in recent numerical studies. Dörr & Kloker (Reference Dörr and Kloker2017) suppressed critical stationary CFI modes and decreased skin friction in a numerical framework, where the distributed PAs successfully excited subcritical stationary CFIs acting as the control mode. The results showed that the PA forcing oriented in both anti-CF and co-CF directions can delay transition, though the anti-CF forcing additionally reduced the mean CF component. Expanding on their previous work, Dörr, Kloker & Hanifi (Reference Dörr, Kloker and Hanifi2017) applied discrete PAs in a boundary layer dominated by travelling CFIs. The PA forcing in both directions was found to significantly damp the growth of travelling CFIs. The outcome demonstrated the stabilising effect of a deformed mean flow which appeared after the plasma-induced subcritical modes. Following the same approach, Shahriari, Kollert & Hanifi (Reference Shahriari, Kollert and Hanifi2018) achieved a successful transition delay in numerical simulations, by enhancing subcritical modes through ring-type PAs. Additionally, subcritical travelling CFI modes were also found beneficial for delaying transition. In the numerical work of Guo & Kloker (Reference Guo and Kloker2019), anti-CF PAs excited positive subcritical travelling CFI modes, acting as the control mechanism. The results demonstrated the ability of subcritical travelling CFI modes in suppressing both critical stationary and travelling CFI modes, thus achieving skin friction reduction.
(ii) Direct attenuation strategy. This strategy is targeted towards directly attenuating the rotational strength (i.e. circulation) of primary stationary CF vortices. Essentially, the PA works in the direct opposition mode, analogous to the Tollmien–Schlichting wave cancellation techniques applied in two-dimensional boundary layers (Grundmann & Tropea Reference Grundmann and Tropea2008; Kotsonis et al. Reference Kotsonis, Giepman, Hulshoff and Veldhuis2013). Dörr & Kloker (Reference Dörr and Kloker2016) achieved the reduction of stationary CF vortices by configuring and orienting the PA forcing in both co-CF and anti-CF directions. The PA position (with respect to the local CF vortex axis) was found to be a key parameter defining the eventual reduction of CF vortex circulation. Similarly, the optimal spanwise position of PAs was investigated in Wang, Wang & Fu (Reference Wang, Wang and Fu2017) where the nonlinear parabolised stability equations combined with sensitivity analyses were solved. While previous studies have been largely numerical, Yadala et al. (Reference Yadala, Hehner, Serpieri, Benard and Kotsonis2018b, Reference Yadala, Hehner, Serpieri, Benard and Kotsonis2021) experimentally achieved transition delay with a comb-type PA which forced a subcritical mode. However, no clear subcritical modulation was observed though the transition was delayed about 3.5 % of the chord length. Guo & Kloker (Reference Guo and Kloker2020) argued that this success was more related to the direct attenuation strategy, due to the strong dependence of transition delay on the spanwise positioning (i.e. phase) of PAs.
(iii) Base flow modification (BFM) strategy. In the BFM method, one or more PAs are installed near the wing leading edge and oriented to directly oppose the CF component. This method is analogous to the aforementioned suction-slot approach where the CF component is directly reduced. Specifically, close to the attachment line of a swept-wing leading edge, inviscid streamlines are directed almost parallel to the leading edge (i.e. ![]() $z$ axis, as shown in figure 1b). As such, the PA forcing in a direction perpendicular to the leading edge (i.e.
$z$ axis, as shown in figure 1b). As such, the PA forcing in a direction perpendicular to the leading edge (i.e. ![]() $-x$ direction) can be utilised to directly counter the CF component. The CF reduction is expected to invoke a global stabilisation of the boundary layer, thus suppressing the growth of both stationary and travelling CFIs. In an early numerical work of Dörr & Kloker (Reference Dörr and Kloker2015), the CF component was reduced by subcritically spaced PAs, modelled as volume distributed body forces. The boundary layer stabilisation was found to be a result of the combination of base flow deformation and three-dimensional flow modulation (i.e. the conditioning of subcritical modes). Yadala et al. (Reference Yadala, Hehner, Serpieri, Benard, Dörr, Kloker and Kotsonis2018a) were the first to experimentally demonstrate transition delay on a swept-wing model using a spanwise-invariant (i.e. two-dimensional) straight PA in the BFM configuration. A simplified numerical model (first proposed by Serpieri et al. (Reference Serpieri, Venkata and Kotsonis2017)) combined with an experimentally characterised body force distribution additionally confirmed the general stabilisation. In a similar study, Serpieri et al. (Reference Serpieri, Venkata and Kotsonis2017) used a two-dimensional straight PA positioned at approximately 2.5 % of wing chord and operated at high forcing frequency (
$-x$ direction) can be utilised to directly counter the CF component. The CF reduction is expected to invoke a global stabilisation of the boundary layer, thus suppressing the growth of both stationary and travelling CFIs. In an early numerical work of Dörr & Kloker (Reference Dörr and Kloker2015), the CF component was reduced by subcritically spaced PAs, modelled as volume distributed body forces. The boundary layer stabilisation was found to be a result of the combination of base flow deformation and three-dimensional flow modulation (i.e. the conditioning of subcritical modes). Yadala et al. (Reference Yadala, Hehner, Serpieri, Benard, Dörr, Kloker and Kotsonis2018a) were the first to experimentally demonstrate transition delay on a swept-wing model using a spanwise-invariant (i.e. two-dimensional) straight PA in the BFM configuration. A simplified numerical model (first proposed by Serpieri et al. (Reference Serpieri, Venkata and Kotsonis2017)) combined with an experimentally characterised body force distribution additionally confirmed the general stabilisation. In a similar study, Serpieri et al. (Reference Serpieri, Venkata and Kotsonis2017) used a two-dimensional straight PA positioned at approximately 2.5 % of wing chord and operated at high forcing frequency (![]() $\,f_{AC}$). Low-frequency velocity fluctuations were found amplified downstream. By means of linear stability theory (LST) and a simplified body force model, the authors attributed the low-frequency fluctuations to inherent unsteadiness in the plasma forcing, possibly related to the stochastic dynamics of electrical discharge. Baranov et al. (Reference Baranov, Chernyshev, Khomich, Kiselev, Kuryachii, Moshkunov, Rebrov, Sboev, Tolkachev and Yamshchikov2021) placed what they call a multi-discharge actuator in subcritical spacing at a chordwise position where the spatial amplification of critical modes reached a maximum. As a result, the mean CF was reduced and critical stationary CF vortices were suppressed without triggering significant subcritical modes. However, the uncontrolled and seemingly random unsteady disturbances produced by the multi-discharge actuator resulted in an anticipated development of secondary CFIs thus triggering earlier transition. By estimating the transition movement and the net power gain from drag reduction, Yadala et al. (Reference Yadala, Hehner, Serpieri, Benard and Kotsonis2021) found the BFM strategy more robust but less effective than the UFD strategy, due to the higher input power. Following the work of Yadala et al. (Reference Yadala, Hehner, Serpieri, Benard, Dörr, Kloker and Kotsonis2018a), Peng et al. (Reference Peng, Arkesteijn, Avallone and Kotsonis2022a) provided the first direct experimental confirmation that the plasma-based BFM can reduce the CF component. More importantly, the PA forcing was found to impose two competing effects in the boundary layer, namely the reduction of stationary CFIs and the enhancement of travelling CFIs.
$\,f_{AC}$). Low-frequency velocity fluctuations were found amplified downstream. By means of linear stability theory (LST) and a simplified body force model, the authors attributed the low-frequency fluctuations to inherent unsteadiness in the plasma forcing, possibly related to the stochastic dynamics of electrical discharge. Baranov et al. (Reference Baranov, Chernyshev, Khomich, Kiselev, Kuryachii, Moshkunov, Rebrov, Sboev, Tolkachev and Yamshchikov2021) placed what they call a multi-discharge actuator in subcritical spacing at a chordwise position where the spatial amplification of critical modes reached a maximum. As a result, the mean CF was reduced and critical stationary CF vortices were suppressed without triggering significant subcritical modes. However, the uncontrolled and seemingly random unsteady disturbances produced by the multi-discharge actuator resulted in an anticipated development of secondary CFIs thus triggering earlier transition. By estimating the transition movement and the net power gain from drag reduction, Yadala et al. (Reference Yadala, Hehner, Serpieri, Benard and Kotsonis2021) found the BFM strategy more robust but less effective than the UFD strategy, due to the higher input power. Following the work of Yadala et al. (Reference Yadala, Hehner, Serpieri, Benard, Dörr, Kloker and Kotsonis2018a), Peng et al. (Reference Peng, Arkesteijn, Avallone and Kotsonis2022a) provided the first direct experimental confirmation that the plasma-based BFM can reduce the CF component. More importantly, the PA forcing was found to impose two competing effects in the boundary layer, namely the reduction of stationary CFIs and the enhancement of travelling CFIs.

Figure 1. (a) Cross-section of the ![]() $M3J$ wing (in the
$M3J$ wing (in the ![]() $x$ direction) and experimental pressure coefficient
$x$ direction) and experimental pressure coefficient ![]() $C_p$ at
$C_p$ at ![]() $\alpha =2.5^{\circ }$ and
$\alpha =2.5^{\circ }$ and ![]() $Re=2.5 \times 10^{6}$. (b) Sketch of
$Re=2.5 \times 10^{6}$. (b) Sketch of ![]() $M3J$ with PA installed. The pressure tap locations are displayed by red and blue dashed lines. The dashed boxes indicate fields of view (FOV) for cameras IR-Full and IR-Zoom. Green solid line indicates the projection of the PIV imaging plane.
$M3J$ with PA installed. The pressure tap locations are displayed by red and blue dashed lines. The dashed boxes indicate fields of view (FOV) for cameras IR-Full and IR-Zoom. Green solid line indicates the projection of the PIV imaging plane.
In spite of the effectiveness and advantages of plasma-based LFC for swept-wing transition control, the mentioned strategies have their own limitations, in need for further improvement. The UFD strategy imposes strict requirements for the manufacturing and dimensioning quality of the actuator (e.g. the ‘cross-talk’ phenomenon, where parasitic reverse plasma will be created if electrodes are too narrowly spaced; Benard, Mizuno & Moreau Reference Benard, Mizuno and Moreau2009). Recent improvements in designing PAs for controlling the CF component and CFIs can be found in Baranov et al. (Reference Baranov, Chernyshev, Khomich, Kiselev, Kuryachii, Moshkunov, Rebrov, Sboev, Tolkachev and Yamshchikov2021) and Guo & Kloker (Reference Guo and Kloker2020). Similarly, the direct attenuation strategy requires the localisation of the actuators at specific positions with respect to the natural CF vortices, which can become unfeasible in realistic conditions where the phase or wavelength of incoming CFIs is unknown. In contrast, in view of actuator manufacturing and design considerations, the BFM strategy appears to be the most applicable and robust method, albeit requiring higher energy input to manipulate the base flow, compared with the other two direct instability control methods.
1.2. Net effect and intrinsic forcing unsteadiness in plasma-based BFM
As previously summarised, the efficacy of plasma-based BFM in reducing the CF component and stationary CFIs has been demonstrated in both numerical and experimental studies. However, the effects of plasma-based BFM on specific boundary layer instabilities such as stationary and travelling CFIs can be complex, due to the realistic manifestations of plasma actuators. In these cases, a DBD plasma actuator supplied with AC high-voltage power will excite a strongly dynamic forcing. The PA forcing comprises two parts, namely a steady and unsteady component. One of the sources of unsteady components is directly correlated to the AC power frequency ![]() $f_{AC}$, which is controllable and deterministic. The work of Dörr & Kloker (Reference Dörr and Kloker2016) demonstrated that the unsteady forcing component related to
$f_{AC}$, which is controllable and deterministic. The work of Dörr & Kloker (Reference Dörr and Kloker2016) demonstrated that the unsteady forcing component related to ![]() $f_{AC}$ has negligible effects on the boundary layer transition when a sufficiently high
$f_{AC}$ has negligible effects on the boundary layer transition when a sufficiently high ![]() $f_{AC}$ is selected (e.g. exceeding frequencies of the most amplified primary travelling CFIs and secondary CFIs). Nonetheless, the majority of experimental studies still observe the plasma-caused enhancement of travelling CFIs, even though the PA was operated at very high
$f_{AC}$ is selected (e.g. exceeding frequencies of the most amplified primary travelling CFIs and secondary CFIs). Nonetheless, the majority of experimental studies still observe the plasma-caused enhancement of travelling CFIs, even though the PA was operated at very high ![]() $f_{AC}$ (Serpieri et al. Reference Serpieri, Venkata and Kotsonis2017; Arkesteijn Reference Arkesteijn2021; Peng et al. Reference Peng, Arkesteijn, Avallone and Kotsonis2022a). These results reveal that the unsteady component of realistic PA forcing invokes both deterministic (i.e. related to the
$f_{AC}$ (Serpieri et al. Reference Serpieri, Venkata and Kotsonis2017; Arkesteijn Reference Arkesteijn2021; Peng et al. Reference Peng, Arkesteijn, Avallone and Kotsonis2022a). These results reveal that the unsteady component of realistic PA forcing invokes both deterministic (i.e. related to the ![]() $f_{AC}$) and non-deterministic behaviours. According to several complementary studies, the source of these non-deterministic forcing can be attributed to the quasi-stochastic nature of plasma micro-discharge formations (Serpieri et al. Reference Serpieri, Venkata and Kotsonis2017; Moralev, Selivonin & Ustinov Reference Moralev, Selivonin and Ustinov2019). At atmospheric pressures, the DBD plasma discharge essentially manifests as a series of micro-discharges (e.g. figure 1 in Moralev et al. (Reference Moralev, Selivonin and Ustinov2019)) which exert a hydrodynamic effect on the flow, through instantaneous body force and heat release fields which are three-dimensional (Moralev et al. Reference Moralev, Boytsov, Kazansky and Bityurin2014; Nishida, Nonomura & Abe Reference Nishida, Nonomura and Abe2014). These micro-discharge structures are not spatially or temporally periodic, thus leading to the low-frequency modulation of the plasma forcing. Hereafter, this is referred to as the non-deterministic/quasi-stochastic nature of DBD plasma forcing. Peng, Avallone & Kotsonis (Reference Peng, Avallone and Kotsonis2022b) further experimentally investigated the impacts of PA unsteadiness on the boundary layer dominated by critical stationary CFI modes. The results demonstrated that distinct instabilities such as type I and type III modes could be amplified (depending on frequency
$f_{AC}$) and non-deterministic behaviours. According to several complementary studies, the source of these non-deterministic forcing can be attributed to the quasi-stochastic nature of plasma micro-discharge formations (Serpieri et al. Reference Serpieri, Venkata and Kotsonis2017; Moralev, Selivonin & Ustinov Reference Moralev, Selivonin and Ustinov2019). At atmospheric pressures, the DBD plasma discharge essentially manifests as a series of micro-discharges (e.g. figure 1 in Moralev et al. (Reference Moralev, Selivonin and Ustinov2019)) which exert a hydrodynamic effect on the flow, through instantaneous body force and heat release fields which are three-dimensional (Moralev et al. Reference Moralev, Boytsov, Kazansky and Bityurin2014; Nishida, Nonomura & Abe Reference Nishida, Nonomura and Abe2014). These micro-discharge structures are not spatially or temporally periodic, thus leading to the low-frequency modulation of the plasma forcing. Hereafter, this is referred to as the non-deterministic/quasi-stochastic nature of DBD plasma forcing. Peng, Avallone & Kotsonis (Reference Peng, Avallone and Kotsonis2022b) further experimentally investigated the impacts of PA unsteadiness on the boundary layer dominated by critical stationary CFI modes. The results demonstrated that distinct instabilities such as type I and type III modes could be amplified (depending on frequency ![]() $f_{AC}$ and chordwise location
$f_{AC}$ and chordwise location ![]() $x/c_x$ of PAs), further influencing the transitional process. Since the micro-discharge formation is an inherent feature of realistic DBD PAs, the excitation of non-deterministic travelling CFIs appears to be an unavoidable effect in plasma-based BFM. This complexifies the transition control goal because the induced travelling CFIs may nonlinearly interact with stationary CFIs, causing a rapid spectral broadening of the perturbation system and ultimately advancing transition, as found by Corke et al. (Reference Corke, Arndt, Matlis and Semper2018) and Arndt et al. (Reference Arndt, Corke, Matlis and Semper2020).
$x/c_x$ of PAs), further influencing the transitional process. Since the micro-discharge formation is an inherent feature of realistic DBD PAs, the excitation of non-deterministic travelling CFIs appears to be an unavoidable effect in plasma-based BFM. This complexifies the transition control goal because the induced travelling CFIs may nonlinearly interact with stationary CFIs, causing a rapid spectral broadening of the perturbation system and ultimately advancing transition, as found by Corke et al. (Reference Corke, Arndt, Matlis and Semper2018) and Arndt et al. (Reference Arndt, Corke, Matlis and Semper2020).
In conclusion, the plasma-based BFM technique comprises two major effects, namely the ‘nominal’ net BFM effect responsible for the global stabilisation of the boundary layer, and an intrinsic forcing unsteadiness which potentially introduces undesired travelling CFIs. Therefore, the successful deployment of plasma-based BFM control necessitates the elucidation of these two competing effects. The present work deploys a range of methodologies to elucidate these effects. Firstly, a low-fidelity numerical evaluation of the net BFM effect on primary stationary and travelling CFI modes is performed, through a simplified CFD and LST model, coupled with an experimentally derived plasma body force distribution. The effects of plasma-based BFM on CFIs and transition are further experimentally investigated by planar particle image velocimetry (PIV) and infrared (IR) thermography, respectively, under variations of critical parameters such as the Reynolds number ![]() $Re$, the angle of attack
$Re$, the angle of attack ![]() $\alpha$ and the wavelength of DRE
$\alpha$ and the wavelength of DRE ![]() $\lambda _{DRE}$.
$\lambda _{DRE}$.
The paper is organised in the following manner. Section 2 gives an introduction to the experimental set-up as well as measurement techniques. Section 3 presents the results of the simplified CFD model, along with a preliminary prediction of net BFM effects using LST. Sections 4 and 5 report PIV and IR thermography measurements and corresponding analyses. Finally, the conclusions of this paper are summarised in § 6.
2. Experimental set-up and methodology
2.1. Wind tunnel facility and swept-wing model
The experimental measurements in this work are performed on the swept-wing model ![]() $66018M3J$ in the Low Turbulence Tunnel at Delft University of Technology. The
$66018M3J$ in the Low Turbulence Tunnel at Delft University of Technology. The ![]() $M3J$ model is extensively used in related experiments by the authors’ research group and is elaborately described by Serpieri & Kotsonis (Reference Serpieri and Kotsonis2015). Owing to the geometry design and sweep angle (
$M3J$ model is extensively used in related experiments by the authors’ research group and is elaborately described by Serpieri & Kotsonis (Reference Serpieri and Kotsonis2015). Owing to the geometry design and sweep angle (![]() $\varLambda =45^{\circ }$), the
$\varLambda =45^{\circ }$), the ![]() $M3J$ model is characterised by extensively favourable pressure gradients on the pressure side, favouring the growth of CFIs. Previous measurements at similar velocity conditions quantified the free-stream turbulence level of the Low Turbulence Tunnel to be
$M3J$ model is characterised by extensively favourable pressure gradients on the pressure side, favouring the growth of CFIs. Previous measurements at similar velocity conditions quantified the free-stream turbulence level of the Low Turbulence Tunnel to be ![]() $T_{u}<0.03\,\%$ (Serpieri Reference Serpieri2018), which guarantees the dominance of stationary CFIs (Bippes Reference Bippes1999).
$T_{u}<0.03\,\%$ (Serpieri Reference Serpieri2018), which guarantees the dominance of stationary CFIs (Bippes Reference Bippes1999).
Measurements are performed at various angles of attack ![]() $\alpha$ and various global
$\alpha$ and various global ![]() $Re$, for which the flow approximately attains infinite swept-wing conditions. Figure 1(a) illustrates the
$Re$, for which the flow approximately attains infinite swept-wing conditions. Figure 1(a) illustrates the ![]() $M3J$ geometry (in the
$M3J$ geometry (in the ![]() $x$ axis) and a representative pressure coefficient
$x$ axis) and a representative pressure coefficient ![]() $C_{p}$ distribution under conditions of
$C_{p}$ distribution under conditions of ![]() $\alpha =2.5^{\circ }$ and
$\alpha =2.5^{\circ }$ and ![]() $Re=2.5\times 10^{6}$. The pressure distributions are measured by the top and bottom pressure tap arrays, illustrated by red and blue dashed lines in figure 1(b). The similarity of the two pressure coefficients confirms the attainment of spanwise-invariant conditions. Two coordinate reference systems are used in this work, namely the tunnel-aligned
$Re=2.5\times 10^{6}$. The pressure distributions are measured by the top and bottom pressure tap arrays, illustrated by red and blue dashed lines in figure 1(b). The similarity of the two pressure coefficients confirms the attainment of spanwise-invariant conditions. Two coordinate reference systems are used in this work, namely the tunnel-aligned ![]() $XYZ$ system and the wing-aligned
$XYZ$ system and the wing-aligned ![]() $xyz$ system, as denoted in figure 1(b). It should be noted that the
$xyz$ system, as denoted in figure 1(b). It should be noted that the ![]() $y$ axis is body-fitted and aligns with the wall-normal direction of the local wing surface. The airfoil chords in directions of
$y$ axis is body-fitted and aligns with the wall-normal direction of the local wing surface. The airfoil chords in directions of ![]() $X$ and
$X$ and ![]() $x$ are denoted as
$x$ are denoted as ![]() $c_X$ and
$c_X$ and ![]() $c_x$, respectively. The velocity vectors corresponding to the two coordinate systems are denoted as
$c_x$, respectively. The velocity vectors corresponding to the two coordinate systems are denoted as ![]() $[UVW]$ and
$[UVW]$ and ![]() $[uvw]$, respectively.
$[uvw]$, respectively.
For the entirety of this work, non-dimensional quantities are denoted by the overbar symbol. In § 3, the numerical velocity quantities are non-dimensionalised by the free-stream velocity ![]() $u_\infty$ corresponding to
$u_\infty$ corresponding to ![]() $Re=2.5\times 10^6$. Whereas in § 4, various
$Re=2.5\times 10^6$. Whereas in § 4, various ![]() $Re$ cases are considered (
$Re$ cases are considered (![]() $2.5\times 10^6$–
$2.5\times 10^6$–![]() $3.7\times 10^6$). Therefore, the PIV-measured velocity components for various
$3.7\times 10^6$). Therefore, the PIV-measured velocity components for various ![]() $Re$ cases are non-dimensionalised by the corresponding free-stream velocity
$Re$ cases are non-dimensionalised by the corresponding free-stream velocity ![]() $U_\infty$. The spanwise distance
$U_\infty$. The spanwise distance ![]() $z$ and wall-normal distance
$z$ and wall-normal distance ![]() $y$ are non-dimensionalised by the global reference length
$y$ are non-dimensionalised by the global reference length ![]() $\delta _0$. Specifically,
$\delta _0$. Specifically, ![]() $\delta _0$ is the Blasius length scale identified in the simplified model of § 3. Parameter
$\delta _0$ is the Blasius length scale identified in the simplified model of § 3. Parameter ![]() $\delta _0$ is calculated as
$\delta _0$ is calculated as ![]() $\delta _0=\sqrt {\nu s_0/u_0}$, where
$\delta _0=\sqrt {\nu s_0/u_0}$, where ![]() $u_0$ is the boundary layer edge velocity at
$u_0$ is the boundary layer edge velocity at ![]() $x/c_x=0.0083$ (the calculation starting point). Viscosity
$x/c_x=0.0083$ (the calculation starting point). Viscosity ![]() $\nu$ refers to the air kinematic viscosity and
$\nu$ refers to the air kinematic viscosity and ![]() $s_0$ is the surface distance from the stagnation point to
$s_0$ is the surface distance from the stagnation point to ![]() $x/c_x=0.0083$. The scaling parameters used in the numerical calculation in § 3 are summarised in table 1. To facilitate the discussion, the terms plasma-off and plasma-on are used to refer to scenarios where PA is not activated and activated, respectively. The quantities at conditions of plasma-off and plasma-on are distinguished by the subscripts ‘off’ and ‘on’, respectively.
$x/c_x=0.0083$. The scaling parameters used in the numerical calculation in § 3 are summarised in table 1. To facilitate the discussion, the terms plasma-off and plasma-on are used to refer to scenarios where PA is not activated and activated, respectively. The quantities at conditions of plasma-off and plasma-on are distinguished by the subscripts ‘off’ and ‘on’, respectively.
Table 1. Scaling parameters pertaining to numerical base flow simulations (![]() $\alpha =2.5^{\circ }$).
$\alpha =2.5^{\circ }$).
2.2. Stationary CFI conditioning and PA
As described in the introduction, swept-wing boundary layers are essentially dominated by stationary CFIs in realistic flight circumstances, due to the extremely low free-stream turbulence intensity ![]() $T_{u}$. In order to elucidate the BFM effects on such flow, the existence and development of stationary CFIs are required in the boundary layer. To this goal, two types of surface roughness arrays are designed and manufactured to enhance stationary CFIs. Specifically, a distributed roughness patch (DRP) is used to trigger a broad spectrum of stationary CFIs, appearing in non-deterministic spanwise wavelengths. The DRP is simply formed by layers of spray-on adhesive, which enhances the wing surface roughness through the random deposition of adhesive particles. To confine the spatial extend of the DRP, a rectangular PVC mask is used. Ultimately, the DRP is generated parallel to the leading edge, spanning from
$T_{u}$. In order to elucidate the BFM effects on such flow, the existence and development of stationary CFIs are required in the boundary layer. To this goal, two types of surface roughness arrays are designed and manufactured to enhance stationary CFIs. Specifically, a distributed roughness patch (DRP) is used to trigger a broad spectrum of stationary CFIs, appearing in non-deterministic spanwise wavelengths. The DRP is simply formed by layers of spray-on adhesive, which enhances the wing surface roughness through the random deposition of adhesive particles. To confine the spatial extend of the DRP, a rectangular PVC mask is used. Ultimately, the DRP is generated parallel to the leading edge, spanning from ![]() $x/c_x = 0.015$ to 0.025.
$x/c_x = 0.015$ to 0.025.
In contrast, for triggering deterministic, single-wavelength modes, arrays of DREs are used. Several DRE arrays of various spanwise spacings (i.e. ![]() $\lambda _{DRE}=6$, 8 and 10 mm) are designed and fabricated in-house. A computer-controlled laser cutting machine is used to shape self-adhesive black PVC foil with thickness of
$\lambda _{DRE}=6$, 8 and 10 mm) are designed and fabricated in-house. A computer-controlled laser cutting machine is used to shape self-adhesive black PVC foil with thickness of ![]() $100\,\mathrm {\mu } {\rm m}$. Each DRE array is installed at
$100\,\mathrm {\mu } {\rm m}$. Each DRE array is installed at ![]() $x/c_{x}=0.02$, just upstream of the neutral point of the forced modes. For the same material and fabrication procedure, a shape characterisation of the fabricated DRP and DREs is described in the work of Zoppini et al. (Reference Zoppini, Michelis, Ragni and Kotsonis2022a,Reference Zoppini, Westerbeek, Ragni and Kotsonisb). The reported geometrical parameters of DRP and DREs are summarised in table 2. Hereafter, the symbols
$x/c_{x}=0.02$, just upstream of the neutral point of the forced modes. For the same material and fabrication procedure, a shape characterisation of the fabricated DRP and DREs is described in the work of Zoppini et al. (Reference Zoppini, Michelis, Ragni and Kotsonis2022a,Reference Zoppini, Westerbeek, Ragni and Kotsonisb). The reported geometrical parameters of DRP and DREs are summarised in table 2. Hereafter, the symbols ![]() $\lambda _6$,
$\lambda _6$, ![]() $\lambda _8$ and
$\lambda _8$ and ![]() $\lambda _{10}$ refer to the dimensional wavelengths of 6, 8 and 10 mm. These wavelengths are non-dimensionalised by
$\lambda _{10}$ refer to the dimensional wavelengths of 6, 8 and 10 mm. These wavelengths are non-dimensionalised by ![]() $\delta _{0}$, resulting in
$\delta _{0}$, resulting in ![]() $\bar {\lambda }_6=50$,
$\bar {\lambda }_6=50$, ![]() $\bar {\lambda }_8=66.67$ and
$\bar {\lambda }_8=66.67$ and ![]() $\bar {\lambda }_{10}=83.33$.
$\bar {\lambda }_{10}=83.33$.
Table 2. Geometric parameters and chord locations of roughness arrays.
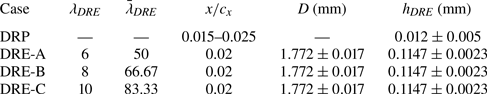
To enable plasma-based BFM, a two-dimensional spanwise-invariant DBD PA is utilised, similar to the type used by Yadala et al. (Reference Yadala, Hehner, Serpieri, Benard, Dörr, Kloker and Kotsonis2018a) and Peng et al. (Reference Peng, Arkesteijn, Avallone and Kotsonis2022a). The PA is fabricated using an automated metal deposition technique developed in-house, where electrodes are printed by sub-micrometric conductive silver spray. The resulting PA electrodes feature a thickness of a few micrometres, imposing negligible roughness effects on the boundary layer (Serpieri et al. Reference Serpieri, Venkata and Kotsonis2017; Yadala et al. Reference Yadala, Hehner, Serpieri, Benard, Dörr, Kloker and Kotsonis2018a). Both exposed and encapsulated electrodes feature a streamwise width (i.e. along the ![]() $x$ direction) of 5 mm with no gap between each other. Specifically, the encapsulated electrode is configured upstream of the exposed electrode with the interface located at
$x$ direction) of 5 mm with no gap between each other. Specifically, the encapsulated electrode is configured upstream of the exposed electrode with the interface located at ![]() $x/c_{x}=0.035$. Following the BFM control principle, the encapsulated electrode is connected to the ground and the exposed electrode is connected to the high-voltage signal, thus generating a body force vector largely oriented in the
$x/c_{x}=0.035$. Following the BFM control principle, the encapsulated electrode is connected to the ground and the exposed electrode is connected to the high-voltage signal, thus generating a body force vector largely oriented in the ![]() $-x$ direction, counteracting the CF component. A polyethylene terephthalate foil with a thickness of
$-x$ direction, counteracting the CF component. A polyethylene terephthalate foil with a thickness of ![]() $500\,\mathrm {\mu } {\rm m}$ is used as the dielectric material, which is further wrapped around the wing leading edge and extends downstream to avoid potential surface irregularities. For the entirety of this work, the PA is powered by a GBS Electronik Minipuls 4 high-voltage amplifier, where the actuation frequency
$500\,\mathrm {\mu } {\rm m}$ is used as the dielectric material, which is further wrapped around the wing leading edge and extends downstream to avoid potential surface irregularities. For the entirety of this work, the PA is powered by a GBS Electronik Minipuls 4 high-voltage amplifier, where the actuation frequency ![]() $f_{AC}$ is set at 12.5 kHz. Though the supplied voltage
$f_{AC}$ is set at 12.5 kHz. Though the supplied voltage ![]() $V_{p-p}$ is set at 7 kV for the body force characterisation experiment (§ 3),
$V_{p-p}$ is set at 7 kV for the body force characterisation experiment (§ 3), ![]() $V_{p-p}$ is set at 6.5 kV for subsequent IR and PIV measurements in the wind tunnel (§§ 4 and 5). This choice is aimed at mitigating electrode degradation resulting from lengthy operation during measurements. Nonetheless, this small difference in
$V_{p-p}$ is set at 6.5 kV for subsequent IR and PIV measurements in the wind tunnel (§§ 4 and 5). This choice is aimed at mitigating electrode degradation resulting from lengthy operation during measurements. Nonetheless, this small difference in ![]() $V_{p-p}$ is assumed to minimally affect the PA forcing strength and spatial distribution, allowing for a qualitative reflection of the physics underlying the experimental findings.
$V_{p-p}$ is assumed to minimally affect the PA forcing strength and spatial distribution, allowing for a qualitative reflection of the physics underlying the experimental findings.
2.3. Planar PIV
Velocity vector fields are extracted by planar PIV for various ![]() $Re$ conditions while the
$Re$ conditions while the ![]() $M3J$ model is set at
$M3J$ model is set at ![]() $\alpha =2.5^{\circ }$. Micrometre-diameter seeding particles are illuminated by a Quantel Evergreen Nd:YAG dual-cavity laser (200 mJ at a wavelength of 532 nm), providing a laser sheet aligned to the
$\alpha =2.5^{\circ }$. Micrometre-diameter seeding particles are illuminated by a Quantel Evergreen Nd:YAG dual-cavity laser (200 mJ at a wavelength of 532 nm), providing a laser sheet aligned to the ![]() $yz$ plane at
$yz$ plane at ![]() $x/c_{x}=0.175$. Per test case, one LaVision imager camera (sCMOS,
$x/c_{x}=0.175$. Per test case, one LaVision imager camera (sCMOS, ![]() $2560\,{\rm px} \times 2160\,{\rm px}$) acquires 600 image pairs at a sampling frequency of 15 Hz. For the various
$2560\,{\rm px} \times 2160\,{\rm px}$) acquires 600 image pairs at a sampling frequency of 15 Hz. For the various ![]() $Re$ cases, the inter-frame time interval of image pairs is appropriately adjusted such that the free-stream particle displacement is around 12 pixels. Particle images are further processed in LaVision Davis 10 through the cross-correlation to obtain the velocity vector
$Re$ cases, the inter-frame time interval of image pairs is appropriately adjusted such that the free-stream particle displacement is around 12 pixels. Particle images are further processed in LaVision Davis 10 through the cross-correlation to obtain the velocity vector ![]() $[vw]$. Each image pair is processed through a multi-pass cross-correlation algorithm with a final interrogation window of
$[vw]$. Each image pair is processed through a multi-pass cross-correlation algorithm with a final interrogation window of ![]() $12\,{\rm px} \times 12\,{\rm px}$ and 50 % overlap. The average flow field is constructed as the average of 600 instantaneous PIV vector fields. Considering laser light reflections and significant velocity uncertainty near the wall, the velocity vectors in that region (
$12\,{\rm px} \times 12\,{\rm px}$ and 50 % overlap. The average flow field is constructed as the average of 600 instantaneous PIV vector fields. Considering laser light reflections and significant velocity uncertainty near the wall, the velocity vectors in that region (![]() $y<0.3\,{\rm mm}$) are discarded in subsequent analyses due to the low reliability. Additionally,
$y<0.3\,{\rm mm}$) are discarded in subsequent analyses due to the low reliability. Additionally, ![]() $y_{min}$ refers to
$y_{min}$ refers to ![]() $y=0.3\,{\rm mm}$ for the entirety of the work. The case of DRE-A at
$y=0.3\,{\rm mm}$ for the entirety of the work. The case of DRE-A at ![]() $Re=3.7\times 10^{6}$, which is anticipated to have the highest level of velocity uncertainty, is used to compute the time-averaged uncertainty. As a consequence, the maximum uncertainty for
$Re=3.7\times 10^{6}$, which is anticipated to have the highest level of velocity uncertainty, is used to compute the time-averaged uncertainty. As a consequence, the maximum uncertainty for ![]() $w$ is found as
$w$ is found as ![]() $0.5\,\%U_{\infty }$ in the boundary layer region, while the average uncertainty is identified as
$0.5\,\%U_{\infty }$ in the boundary layer region, while the average uncertainty is identified as ![]() $0.012\,\%U_{\infty }$ in the free-stream region. Additionally, the combinations of tested
$0.012\,\%U_{\infty }$ in the free-stream region. Additionally, the combinations of tested ![]() $Re$ and
$Re$ and ![]() $\alpha$ for PIV as well as IR measurements are summarised in table 3.
$\alpha$ for PIV as well as IR measurements are summarised in table 3.
Table 3. Reynolds number ![]() $Re$ and
$Re$ and ![]() $\alpha$ combinations for PIV and IR measurements.
$\alpha$ combinations for PIV and IR measurements.

2.4. Infrared thermography
According to the Reynolds analogy, in boundary layer flows the rate of heat convection is a direct function of local wall shear stress. As such, for a given heat flux, variations in shear stress will result in surface temperature differences, which can be identified through IR thermography. This non-intrusive technique is extensively used in associated studies by the authors’ research group, which has been proven as expeditious in visualising the thermal footprint of stationary CF vortices and the resulting laminar–turbulent transition front (Rius-Vidales & Kotsonis Reference Rius-Vidales and Kotsonis2020; Zoppini et al. Reference Zoppini, Westerbeek, Ragni and Kotsonis2022b).
In the current experiment, two Optris PI640 IR cameras (![]() $640\,{\rm px} \times 480\,{\rm px}$, NETID 75 mK) are utilised to measure the wing surface temperature. The first camera coupled with a wide-angle lens (
$640\,{\rm px} \times 480\,{\rm px}$, NETID 75 mK) are utilised to measure the wing surface temperature. The first camera coupled with a wide-angle lens (![]() $\,f_\#=10.5\,{\rm mm}$) is designated as IR-Full and captures the entire wing surface temperature. The second camera, named IR-Zoom, is coupled with a telephoto lens (
$\,f_\#=10.5\,{\rm mm}$) is designated as IR-Full and captures the entire wing surface temperature. The second camera, named IR-Zoom, is coupled with a telephoto lens (![]() $\,f_\#=41.5\,{\rm mm}$), imaging a small region in the middle of the wing (domain outlined by the magenta box of figure 2a, from
$\,f_\#=41.5\,{\rm mm}$), imaging a small region in the middle of the wing (domain outlined by the magenta box of figure 2a, from ![]() $x/c_{x}=0.0565$ to 0.2385). Approximately 40 images are recorded by these cameras for each run at a sampling frequency
$x/c_{x}=0.0565$ to 0.2385). Approximately 40 images are recorded by these cameras for each run at a sampling frequency ![]() $f_s=4\,{\rm Hz}$, which are later time-averaged to reduce background noise. Additionally, several halogen lamps are used to radiate the wing model in order to improve the thermal contrast.
$f_s=4\,{\rm Hz}$, which are later time-averaged to reduce background noise. Additionally, several halogen lamps are used to radiate the wing model in order to improve the thermal contrast.

Figure 2. Time-average IR images of transition front visualisation (DRE-B, ![]() $\alpha =2.5^{\circ }$ and
$\alpha =2.5^{\circ }$ and ![]() $Re=3.3\times 10^{6}$) for (a) PA-off and (b) PA-on. Flow comes from the left and the leading edge is shown by the black line. The PA location is indicated by red dashed line. (c) Subtraction of IR image of (a,b). Gained laminar flow (magenta) and lost laminar flow (cyan). (d) Simple sketch for clarifying the transformation between the net laminar gain and transition location shift (not to scale).
$Re=3.3\times 10^{6}$) for (a) PA-off and (b) PA-on. Flow comes from the left and the leading edge is shown by the black line. The PA location is indicated by red dashed line. (c) Subtraction of IR image of (a,b). Gained laminar flow (magenta) and lost laminar flow (cyan). (d) Simple sketch for clarifying the transformation between the net laminar gain and transition location shift (not to scale).
Typical time-average IR images of the transition front are shown in figure 2(a,b). Specifically, the turbulent region presents darker tone while the laminar region shows brighter tone. Figure 2(c) illustrates the IR intensity subtraction ![]() $\Delta I$ between panels (a) and (b). The white area (near the transition front) corresponds to the gained laminar flow (i.e. transition delay) and the black area corresponds to the gained turbulent flow (transition advance). For this work, the gained laminar area
$\Delta I$ between panels (a) and (b). The white area (near the transition front) corresponds to the gained laminar flow (i.e. transition delay) and the black area corresponds to the gained turbulent flow (transition advance). For this work, the gained laminar area ![]() $s_l$ can be roughly identified as regions of
$s_l$ can be roughly identified as regions of ![]() $\Delta I>\Delta I_r$ while the lost laminar area
$\Delta I>\Delta I_r$ while the lost laminar area ![]() $s_t$ is identified as regions of
$s_t$ is identified as regions of ![]() $\Delta I<-\Delta I_r$, where
$\Delta I<-\Delta I_r$, where ![]() $\Delta I_r$ is a threshold value. Variations of the threshold value are tested in order to identify the sensitivity of gained and lost laminar flow areas. Reasonable areas of gained and lost laminar flow can be identified with a threshold between 0.3 and 0.6. As a result,
$\Delta I_r$ is a threshold value. Variations of the threshold value are tested in order to identify the sensitivity of gained and lost laminar flow areas. Reasonable areas of gained and lost laminar flow can be identified with a threshold between 0.3 and 0.6. As a result, ![]() $\Delta I_r=0.4$ is chosen as the threshold for the subsequent processing. Though the threshold of 0.4 is chosen heuristically, it remains constant for the entire parameter range to produce comparable outcomes. Typical results of
$\Delta I_r=0.4$ is chosen as the threshold for the subsequent processing. Though the threshold of 0.4 is chosen heuristically, it remains constant for the entire parameter range to produce comparable outcomes. Typical results of ![]() $s_l$ and
$s_l$ and ![]() $s_t$ are given in figure 2(c), outlined by the magenta and cyan lines, respectively (at the threshold of 0.4). Consequently, the net laminar gain is calculated as
$s_t$ are given in figure 2(c), outlined by the magenta and cyan lines, respectively (at the threshold of 0.4). Consequently, the net laminar gain is calculated as ![]() $s_l-s_t$. The net laminar gain is further transformed to an equivalent transition location shift
$s_l-s_t$. The net laminar gain is further transformed to an equivalent transition location shift ![]() $\Delta (x_t/c_x)$ used in the discussion in § 5.2. Figure 2(d) depicts a simple sketch which aids in clarifying the transformation. Using the area rule of a parallelogram, an equivalent spanwise-invariant transition location shift is found as a function of the net laminar area gain, as shown by (2.1):
$\Delta (x_t/c_x)$ used in the discussion in § 5.2. Figure 2(d) depicts a simple sketch which aids in clarifying the transformation. Using the area rule of a parallelogram, an equivalent spanwise-invariant transition location shift is found as a function of the net laminar area gain, as shown by (2.1):
where ![]() $s_r$ refers to the constant area between
$s_r$ refers to the constant area between ![]() $x/c_{x}=0.1$ and 0.2 (blue area) and
$x/c_{x}=0.1$ and 0.2 (blue area) and ![]() $h$ is the parallelogram height.
$h$ is the parallelogram height.
Beyond the identification of laminar gain or loss, the use of IR thermography also enables access to the nature of laminar breakdown. More specifically, the loss of spatial coherency in the transition front (i.e. ‘blurriness’) can be expected to underline a change between a stationary CFI and travelling CFI scenario (Downs & White Reference Downs and White2013; Borodulin, Ivanov & Kachanov Reference Borodulin, Ivanov and Kachanov2015). As such it is desirable to formalise and quantify this effect. In the field of image processing, a blurred object is characterised by a gradual variation in intensity scale (e.g. IR intensity ![]() $I$ in this paper) along its outline when compared with a sharp object. In the context of this work, the object is the wedged transition front where a blurred wedge edge is expected to exhibit a relatively smaller gradient compared to a sharp edge. Consequently, the detection of transition front blurriness can be facilitated by simply quantifying the IR intensity gradient at edges of transitional wedges. For all tested cases, the general trend of the transition front follows an angle of
$I$ in this paper) along its outline when compared with a sharp object. In the context of this work, the object is the wedged transition front where a blurred wedge edge is expected to exhibit a relatively smaller gradient compared to a sharp edge. Consequently, the detection of transition front blurriness can be facilitated by simply quantifying the IR intensity gradient at edges of transitional wedges. For all tested cases, the general trend of the transition front follows an angle of ![]() $45^{\circ }$ with the
$45^{\circ }$ with the ![]() $X$ axis, highlighting the importance of both
$X$ axis, highlighting the importance of both ![]() $x$ gradient and
$x$ gradient and ![]() $y$ gradient of
$y$ gradient of ![]() $I$. As a result, the intensity gradient
$I$. As a result, the intensity gradient ![]() $|\boldsymbol {\nabla } I|=\sqrt {|{\partial I}/{\partial x}|^2+|{\partial I}/{\partial y}|^2}$ is calculated for all cases and representative results are displayed in figure 3(b,e). In general, plasma-off cases result in intensified
$|\boldsymbol {\nabla } I|=\sqrt {|{\partial I}/{\partial x}|^2+|{\partial I}/{\partial y}|^2}$ is calculated for all cases and representative results are displayed in figure 3(b,e). In general, plasma-off cases result in intensified ![]() $|\boldsymbol {\nabla } I|$ values outlining the typical wedged transition front, while plasma-on cases result in minimal
$|\boldsymbol {\nabla } I|$ values outlining the typical wedged transition front, while plasma-on cases result in minimal ![]() $|\boldsymbol {\nabla } I|$ due to the blurred transition front. Similar results of
$|\boldsymbol {\nabla } I|$ due to the blurred transition front. Similar results of ![]() $|\boldsymbol {\nabla } I|$ are found for the majority of tested cases (not shown here for brevity), demonstrating the efficacy of
$|\boldsymbol {\nabla } I|$ are found for the majority of tested cases (not shown here for brevity), demonstrating the efficacy of ![]() $|\boldsymbol {\nabla } I|$ as an indication of the transition front blurriness. The intensity gradient
$|\boldsymbol {\nabla } I|$ as an indication of the transition front blurriness. The intensity gradient ![]() $|\boldsymbol {\nabla } I|$ is only considered in a mask region (outlined by magenta lines as shown in figure 3) to exclude the strong gradient caused by the PA. Within this mask region, the paper focuses on the
$|\boldsymbol {\nabla } I|$ is only considered in a mask region (outlined by magenta lines as shown in figure 3) to exclude the strong gradient caused by the PA. Within this mask region, the paper focuses on the ![]() $|\boldsymbol {\nabla } I|$ of sufficiently strong values (
$|\boldsymbol {\nabla } I|$ of sufficiently strong values (![]() $|\boldsymbol {\nabla } I|>0.25$) to effectively eliminate background noise. The filtered
$|\boldsymbol {\nabla } I|>0.25$) to effectively eliminate background noise. The filtered ![]() $|\boldsymbol {\nabla } I|$ is illustrated in figure 3(c,f). In the context of this work, the
$|\boldsymbol {\nabla } I|$ is illustrated in figure 3(c,f). In the context of this work, the ![]() $|\boldsymbol {\nabla } I|$ is employed solely as a means to reflect the plasma-caused alteration of transition front blurriness. Through a batch of tests, any threshold value between 0.2 and 0.28 is deemed appropriate for this goal. In this paper, the threshold is arbitrarily chosen as 0.25 and maintained consistently throughout the entire processing, ensuring comparable results. Consequently, the average density of
$|\boldsymbol {\nabla } I|$ is employed solely as a means to reflect the plasma-caused alteration of transition front blurriness. Through a batch of tests, any threshold value between 0.2 and 0.28 is deemed appropriate for this goal. In this paper, the threshold is arbitrarily chosen as 0.25 and maintained consistently throughout the entire processing, ensuring comparable results. Consequently, the average density of ![]() $|\boldsymbol {\nabla } I|$ is identified as
$|\boldsymbol {\nabla } I|$ is identified as ![]() $|\boldsymbol {\nabla } I|_{d}=\varSigma |\boldsymbol {\nabla } I|/s_I$, where
$|\boldsymbol {\nabla } I|_{d}=\varSigma |\boldsymbol {\nabla } I|/s_I$, where ![]() $s_I$ is the mask area outlined by the magenta lines and
$s_I$ is the mask area outlined by the magenta lines and ![]() $\varSigma |\boldsymbol {\nabla } I|$ refers to the sum of
$\varSigma |\boldsymbol {\nabla } I|$ refers to the sum of ![]() $|\boldsymbol {\nabla } I|$ in the mask region.
$|\boldsymbol {\nabla } I|$ in the mask region.

Figure 3. Transition front identification under ![]() $Re=2.5\times 10^6$ and
$Re=2.5\times 10^6$ and ![]() $\alpha =2.5^{\circ }$ (DRE-B). (a,d) Time-average IR images; (b,e) IR intensity gradient
$\alpha =2.5^{\circ }$ (DRE-B). (a,d) Time-average IR images; (b,e) IR intensity gradient ![]() $|\boldsymbol {\nabla } I|$; (c,f) filtered IR intensity gradient (
$|\boldsymbol {\nabla } I|$; (c,f) filtered IR intensity gradient (![]() $|\boldsymbol {\nabla } I|>0.25$).
$|\boldsymbol {\nabla } I|>0.25$).
3. Estimation of net BFM effect through LST
In this section, a simplified PA forcing model used in previous studies (Serpieri et al. Reference Serpieri, Venkata and Kotsonis2017; Yadala et al. Reference Yadala, Hehner, Serpieri, Benard, Dörr, Kloker and Kotsonis2018a; Peng et al. Reference Peng, Arkesteijn, Avallone and Kotsonis2022a) is employed to evaluate the plasma-induced modification of the base flow on the ![]() $M3J$ wing. By using the finite-element multiphysics tool COMSOL, the simplified model essentially solves the incompressible Navier–Stokes equations coupled with a volume-distributed body force term, representing the plasma forcing effect. Specifically, velocity profiles
$M3J$ wing. By using the finite-element multiphysics tool COMSOL, the simplified model essentially solves the incompressible Navier–Stokes equations coupled with a volume-distributed body force term, representing the plasma forcing effect. Specifically, velocity profiles ![]() $[uvw]$ at
$[uvw]$ at ![]() $x/c_{x}=0.083$ are calculated by the boundary layer solver and adopted as inflow boundary conditions of the simplified model (by COMSOL). To obtain the body force distribution of the PA, an additional PIV characterisation experiment is conducted in quiescent flow. Figure 4(a) illustrates the time-average velocity field (
$x/c_{x}=0.083$ are calculated by the boundary layer solver and adopted as inflow boundary conditions of the simplified model (by COMSOL). To obtain the body force distribution of the PA, an additional PIV characterisation experiment is conducted in quiescent flow. Figure 4(a) illustrates the time-average velocity field (![]() $x$ component), which is used to calculate the body force distribution, following the method of Wilke (Reference Wilke2009) and the empirical model proposed by Maden et al. (Reference Maden, Maduta, Kriegseis, Jakirlić, Schwarz, Grundmann and Tropea2013). Figure 4(b) illustrates the estimated body force distribution
$x$ component), which is used to calculate the body force distribution, following the method of Wilke (Reference Wilke2009) and the empirical model proposed by Maden et al. (Reference Maden, Maduta, Kriegseis, Jakirlić, Schwarz, Grundmann and Tropea2013). Figure 4(b) illustrates the estimated body force distribution ![]() $F_{x}$, which is further used in the simplified model as a source term of the Navier–Stokes momentum equations. The streamline-aligned velocity
$F_{x}$, which is further used in the simplified model as a source term of the Navier–Stokes momentum equations. The streamline-aligned velocity ![]() $u_{s}$ and CF component
$u_{s}$ and CF component ![]() $w_{s}$ are calculated based on the transformation used by Peng et al. (Reference Peng, Arkesteijn, Avallone and Kotsonis2022a) and non-dimensionalised as
$w_{s}$ are calculated based on the transformation used by Peng et al. (Reference Peng, Arkesteijn, Avallone and Kotsonis2022a) and non-dimensionalised as ![]() $\bar {u}_{s}$ and
$\bar {u}_{s}$ and ![]() $\bar {w}_{s}$. The plasma-caused alterations are further calculated for
$\bar {w}_{s}$. The plasma-caused alterations are further calculated for ![]() $\bar {u}_{s}$ and
$\bar {u}_{s}$ and ![]() $\bar {w}_{s}$, as defined in (3.1a,b):
$\bar {w}_{s}$, as defined in (3.1a,b):
The results are presented in figure 4(c,d), where the velocity profiles ![]() $u_s/u_{se}$ and
$u_s/u_{se}$ and ![]() $w_s/u_{se}$ are compared at several streamwise chord locations. Particularly,
$w_s/u_{se}$ are compared at several streamwise chord locations. Particularly, ![]() $u_{se}$ is the boundary layer edge velocity of
$u_{se}$ is the boundary layer edge velocity of ![]() $u_{s}$. As expected, both streamline-aligned velocity and CF component are reduced due to the PA forcing. Overall, the current results of
$u_{s}$. As expected, both streamline-aligned velocity and CF component are reduced due to the PA forcing. Overall, the current results of ![]() $\bar {u}_{s}$ and
$\bar {u}_{s}$ and ![]() $\bar {w}_{s}$ show sufficient agreement with the work of Peng et al. (Reference Peng, Arkesteijn, Avallone and Kotsonis2022a) and provide a first quantification of the net BFM effect.
$\bar {w}_{s}$ show sufficient agreement with the work of Peng et al. (Reference Peng, Arkesteijn, Avallone and Kotsonis2022a) and provide a first quantification of the net BFM effect.

Figure 4. (a) Plasma-induced time-average velocity field ![]() $u$ in quiescent conditions. (b) Body force
$u$ in quiescent conditions. (b) Body force ![]() $F_{x}$ (
$F_{x}$ (![]() $x$ component). The dotted line denotes
$x$ component). The dotted line denotes ![]() $F_{x}=10\,\% F_{x,max}$, where
$F_{x}=10\,\% F_{x,max}$, where ![]() $F_{x,max}=\max (F_{x})$. The CF profiles
$F_{x,max}=\max (F_{x})$. The CF profiles ![]() $w_{s}/u_{se}$ are shown at
$w_{s}/u_{se}$ are shown at ![]() $x/c_{x}=0.03$, 0.032 and 0.034 for comparison. The boundary layer thickness
$x/c_{x}=0.03$, 0.032 and 0.034 for comparison. The boundary layer thickness ![]() $\delta _{99}$ is computed under plasma-off conditions. (c) Streamline-aligned velocity reduction
$\delta _{99}$ is computed under plasma-off conditions. (c) Streamline-aligned velocity reduction ![]() $\Delta \bar {u}_{s}$. The
$\Delta \bar {u}_{s}$. The ![]() $u_{s}/u_{e}$ profiles are illustrated at
$u_{s}/u_{e}$ profiles are illustrated at ![]() $x/c_{x}=0.032$, 0.034, 0.036, 0.038 and 0.04 with an abscissa shift of 0.5. (d) Same as (c) but for CF velocity reduction
$x/c_{x}=0.032$, 0.034, 0.036, 0.038 and 0.04 with an abscissa shift of 0.5. (d) Same as (c) but for CF velocity reduction ![]() $\Delta \bar {w}_{s}$ and CF profiles of
$\Delta \bar {w}_{s}$ and CF profiles of ![]() $w_{s}/u_{e}$ (with abscissa shift of 0.1).
$w_{s}/u_{e}$ (with abscissa shift of 0.1).
The LST analysis is consequently performed on the calculated base flow to estimate the critical stationary modes, and further to evaluate the PA effects on various CFI modes. Consequently, non-dimensional spatial growth rate ![]() $-\bar {\alpha }_{i}=-\alpha _i\delta _0$ and
$-\bar {\alpha }_{i}=-\alpha _i\delta _0$ and ![]() $N$ factor (the streamwise integral of
$N$ factor (the streamwise integral of ![]() $-\bar {\alpha }_{i}$) are calculated for both plasma-off and plasma-on conditions. The full theoretical description of LST can be found in Mack (Reference Mack1984), while the numerical implementation is similar to the work of Rius-Vidales & Kotsonis (Reference Rius-Vidales and Kotsonis2020). Several studies have shown that travelling CFI modes essentially consist of negative and positive travelling modes, which propagate along and against the CF direction, respectively. Nonetheless, compared to negative travelling modes, positive travelling modes feature significantly higher growth rates and are more dominant in the boundary layer development (Guo & Kloker Reference Guo and Kloker2019; Peng et al. Reference Peng, Avallone and Kotsonis2022b). Therefore, the following discussion only considers stationary CFI modes and positive travelling CFI modes. Figure 5 illustrates the plasma-induced alteration of non-dimensional growth rate
$-\bar {\alpha }_{i}$) are calculated for both plasma-off and plasma-on conditions. The full theoretical description of LST can be found in Mack (Reference Mack1984), while the numerical implementation is similar to the work of Rius-Vidales & Kotsonis (Reference Rius-Vidales and Kotsonis2020). Several studies have shown that travelling CFI modes essentially consist of negative and positive travelling modes, which propagate along and against the CF direction, respectively. Nonetheless, compared to negative travelling modes, positive travelling modes feature significantly higher growth rates and are more dominant in the boundary layer development (Guo & Kloker Reference Guo and Kloker2019; Peng et al. Reference Peng, Avallone and Kotsonis2022b). Therefore, the following discussion only considers stationary CFI modes and positive travelling CFI modes. Figure 5 illustrates the plasma-induced alteration of non-dimensional growth rate ![]() $\Delta \bar {\alpha }_{i}= (-\bar {\alpha }_{i,on}-(-\bar {\alpha }_{i,off}))$ and
$\Delta \bar {\alpha }_{i}= (-\bar {\alpha }_{i,on}-(-\bar {\alpha }_{i,off}))$ and ![]() $N$ factor, which are denoted by colours and contours, respectively. Based on the
$N$ factor, which are denoted by colours and contours, respectively. Based on the ![]() $N$ factor curves, the critical stationary mode is estimated. The critical stationary mode is determined as the mode featuring the highest
$N$ factor curves, the critical stationary mode is estimated. The critical stationary mode is determined as the mode featuring the highest ![]() $N$ factor at the experimentally observed transition location, under the condition of PA-off. Consequently, the critical stationary mode is determined as
$N$ factor at the experimentally observed transition location, under the condition of PA-off. Consequently, the critical stationary mode is determined as ![]() $8$ mm for
$8$ mm for ![]() $Re=2.5\times 10^6$. Additionally, the critical stationary modes for other
$Re=2.5\times 10^6$. Additionally, the critical stationary modes for other ![]() $Re$ have been estimated, though the corresponding LST results are not provided here for brevity. The resulting critical stationary modes are 7, 6.5, 5, 4.5, 3.5 and 3 mm for
$Re$ have been estimated, though the corresponding LST results are not provided here for brevity. The resulting critical stationary modes are 7, 6.5, 5, 4.5, 3.5 and 3 mm for ![]() $Re=2.7\times 10^6$,
$Re=2.7\times 10^6$, ![]() $2.9\times 10^6$,
$2.9\times 10^6$, ![]() $3.1\times 10^6$,
$3.1\times 10^6$, ![]() $3.3\times 10^6$,
$3.3\times 10^6$, ![]() $3.5\times 10^6$ and
$3.5\times 10^6$ and ![]() $3.7\times 10^6$, respectively. Furthermore,
$3.7\times 10^6$, respectively. Furthermore, ![]() $\Delta \bar {\alpha }_{i}$ as well as the reduction of
$\Delta \bar {\alpha }_{i}$ as well as the reduction of ![]() $N$ factors indicate that both stationary and travelling CFI modes are reduced via the net BFM effect due to the reduction of their source, namely the CF component, agreeing well with previous studies (Dörr & Kloker Reference Dörr and Kloker2015; Serpieri et al. Reference Serpieri, Venkata and Kotsonis2017; Peng et al. Reference Peng, Arkesteijn, Avallone and Kotsonis2022a). Near the PA location, travelling CFI modes appear to suffer a larger reduction of growth rates, especially those of smaller wavelengths. This disproportionate reduction of stationary and travelling CFI modes is also observed by Dörr & Kloker (Reference Dörr and Kloker2015), Guo & Kloker (Reference Guo and Kloker2019) and Peng et al. (Reference Peng, Arkesteijn, Avallone and Kotsonis2022a), which may be related to the distinct wavenumber vector directions of these modes, as suggested by Guo & Kloker (Reference Guo and Kloker2019).
$N$ factors indicate that both stationary and travelling CFI modes are reduced via the net BFM effect due to the reduction of their source, namely the CF component, agreeing well with previous studies (Dörr & Kloker Reference Dörr and Kloker2015; Serpieri et al. Reference Serpieri, Venkata and Kotsonis2017; Peng et al. Reference Peng, Arkesteijn, Avallone and Kotsonis2022a). Near the PA location, travelling CFI modes appear to suffer a larger reduction of growth rates, especially those of smaller wavelengths. This disproportionate reduction of stationary and travelling CFI modes is also observed by Dörr & Kloker (Reference Dörr and Kloker2015), Guo & Kloker (Reference Guo and Kloker2019) and Peng et al. (Reference Peng, Arkesteijn, Avallone and Kotsonis2022a), which may be related to the distinct wavenumber vector directions of these modes, as suggested by Guo & Kloker (Reference Guo and Kloker2019).

Figure 5. (a) Change of growth rate ![]() $\Delta \bar {\alpha }_i$ (coloured) and
$\Delta \bar {\alpha }_i$ (coloured) and ![]() $N$ factors (iso-lines) for various CFI modes. The
$N$ factors (iso-lines) for various CFI modes. The ![]() $N$ factor iso-lines increase from 1 with an interval of 1 (starting from left). The triangle indicates the PA location. (b) The
$N$ factor iso-lines increase from 1 with an interval of 1 (starting from left). The triangle indicates the PA location. (b) The ![]() $N$ factor curves (from a) for selected CFI modes. The red and black vertical dashed lines indicate locations of DRE and PA intersection, respectively.
$N$ factor curves (from a) for selected CFI modes. The red and black vertical dashed lines indicate locations of DRE and PA intersection, respectively.
Considering the potential inception and amplification of travelling CFI modes through realistic PA operation (i.e. deterministic and non-deterministic unsteady PA forcing), it becomes intriguing to investigate the plasma-caused alterations of the boundary layer's response to stationary and travelling CFI modes. Despite the localised momentum modification due to the PA forcing, its impact on the boundary layer extends considerably downstream. Hence, it is reasonable to compare the ![]() $N$ factor of CFI modes, as it reflects their integrated responses due to the overall alteration of the boundary layer. As such, the ratio of
$N$ factor of CFI modes, as it reflects their integrated responses due to the overall alteration of the boundary layer. As such, the ratio of ![]() $N_t/N_s$ is selected to reflect the susceptibility of the boundary layer to stationary and travelling modes, where
$N_t/N_s$ is selected to reflect the susceptibility of the boundary layer to stationary and travelling modes, where ![]() $N_s$ and
$N_s$ and ![]() $N_t$ refer to
$N_t$ refer to ![]() $N$ factors of stationary and travelling CFI modes, respectively. The ratio
$N$ factors of stationary and travelling CFI modes, respectively. The ratio ![]() $N_t/N_s$ of two representative cases is illustrated in figures 6(a) and 6(b), where travelling CFI modes are considered at
$N_t/N_s$ of two representative cases is illustrated in figures 6(a) and 6(b), where travelling CFI modes are considered at ![]() $f=200$ and
$f=200$ and ![]() $400\,{\rm Hz}$, respectively, while sharing the same wavelengths
$400\,{\rm Hz}$, respectively, while sharing the same wavelengths ![]() $\bar {\lambda }$ as stationary CFI modes.
$\bar {\lambda }$ as stationary CFI modes.

Figure 6. The ![]() $N$ factor ratio
$N$ factor ratio ![]() $N_{t}/N_{s}$ for CFI modes of (a)
$N_{t}/N_{s}$ for CFI modes of (a) ![]() $f=200\,{\rm Hz}$ and (b)
$f=200\,{\rm Hz}$ and (b) ![]() $f=400\,{\rm Hz}$. (c) Envelope
$f=400\,{\rm Hz}$. (c) Envelope ![]() $N$ factor ratio
$N$ factor ratio ![]() $N^{env}_{t}/N^{env}_{s}$ for various cases.
$N^{env}_{t}/N^{env}_{s}$ for various cases.
A noteworthy observation is that, for both plasma-off and plasma-on, the ratio ![]() $N_t/N_s$ for all examined modes consistently increases from 0 to 1. This phenomenon can be traced to the more upstream locations of the neutral points of stationary CFI modes compared with their travelling counterparts (given the same spanwise wavelength). Nonetheless, the ratio rapidly surpasses 1, due to the more pronounced downstream growth rates of travelling modes. The ratio
$N_t/N_s$ for all examined modes consistently increases from 0 to 1. This phenomenon can be traced to the more upstream locations of the neutral points of stationary CFI modes compared with their travelling counterparts (given the same spanwise wavelength). Nonetheless, the ratio rapidly surpasses 1, due to the more pronounced downstream growth rates of travelling modes. The ratio ![]() $N_t/N_s$ exhibits a noticeably higher value downstream under the plasma-on condition, indicating an enhanced susceptibility of the boundary layer to travelling CFI modes due to the PA forcing. This observation also holds true for other frequencies of travelling modes such as
$N_t/N_s$ exhibits a noticeably higher value downstream under the plasma-on condition, indicating an enhanced susceptibility of the boundary layer to travelling CFI modes due to the PA forcing. This observation also holds true for other frequencies of travelling modes such as ![]() $f=300, 500$ and 600 Hz and is not shown here for brevity. The ratio of envelope
$f=300, 500$ and 600 Hz and is not shown here for brevity. The ratio of envelope ![]() $N$ factors is further calculated for stationary and travelling CFI modes and denoted as
$N$ factors is further calculated for stationary and travelling CFI modes and denoted as ![]() $N_{t}^{env}/N_{s}^{env}$. Figure 6(c) illustrates the ratio
$N_{t}^{env}/N_{s}^{env}$. Figure 6(c) illustrates the ratio ![]() $N_{t}^{env}/N_{s}^{env}$ for the reference case of
$N_{t}^{env}/N_{s}^{env}$ for the reference case of ![]() $Re=2.5\times 10^6$ and an additional case of higher
$Re=2.5\times 10^6$ and an additional case of higher ![]() $Re=3.5\times 10^6$. The CFI modes used to calculate envelope
$Re=3.5\times 10^6$. The CFI modes used to calculate envelope ![]() $N$ factors are selected in the range of most amplified CFI modes (i.e.
$N$ factors are selected in the range of most amplified CFI modes (i.e. ![]() $3\,{\rm mm}\leq \lambda \leq 11.5\,{\rm mm}$ and
$3\,{\rm mm}\leq \lambda \leq 11.5\,{\rm mm}$ and ![]() $0\,{\rm Hz}\leq f \leq 600\,{\rm Hz}$, with an interval of 0.5 mm and 10 Hz, respectively).
$0\,{\rm Hz}\leq f \leq 600\,{\rm Hz}$, with an interval of 0.5 mm and 10 Hz, respectively).
Under unforced flow conditions (plasma-off), the ratio ![]() $N_{t}^{env}/N_{s}^{env}$ shows values greater than 1 for both low- and high-
$N_{t}^{env}/N_{s}^{env}$ shows values greater than 1 for both low- and high-![]() $Re$ cases. This outcome implies that travelling CFIs display higher integrated growth compared with stationary CFI modes, a trend commonly observed across various studies (Bippes Reference Bippes1999; Wassermann & Kloker Reference Wassermann and Kloker2003). However, the ratio
$Re$ cases. This outcome implies that travelling CFIs display higher integrated growth compared with stationary CFI modes, a trend commonly observed across various studies (Bippes Reference Bippes1999; Wassermann & Kloker Reference Wassermann and Kloker2003). However, the ratio ![]() $N_{t}^{env}/N_{s}^{env}$ generally exhibits smaller values at higher
$N_{t}^{env}/N_{s}^{env}$ generally exhibits smaller values at higher ![]() $Re$ compared with lower
$Re$ compared with lower ![]() $Re$. This suggests that while travelling CFI modes indeed exhibit greater integrated growth than stationary CFI modes, the growth discrepancy tends to diminish with increasing
$Re$. This suggests that while travelling CFI modes indeed exhibit greater integrated growth than stationary CFI modes, the growth discrepancy tends to diminish with increasing ![]() $Re$. When the PA is on, the ratio
$Re$. When the PA is on, the ratio ![]() $N_{t}^{env}/N_{s}^{env}$ of both low- and high-
$N_{t}^{env}/N_{s}^{env}$ of both low- and high-![]() $Re$ cases is significantly affected. Evidently, an increase of
$Re$ cases is significantly affected. Evidently, an increase of ![]() $N_{t}^{env}/N_{s}^{env}$ is found downstream of the PA location and its increase becomes more prominent while moving more downstream. This indicates that within the linear growth stage of these CFI modes, the net BFM effect exerts a stronger suppressive effect on stationary CFI modes compared with travelling CFI modes of comparable wavelengths. It is important to note that this conclusion cannot be interpreted as an indication that travelling CFI modes will obtain larger amplitudes (compared with their stationary counterparts) within the boundary layer. This is due to the fact that the ratio
$N_{t}^{env}/N_{s}^{env}$ is found downstream of the PA location and its increase becomes more prominent while moving more downstream. This indicates that within the linear growth stage of these CFI modes, the net BFM effect exerts a stronger suppressive effect on stationary CFI modes compared with travelling CFI modes of comparable wavelengths. It is important to note that this conclusion cannot be interpreted as an indication that travelling CFI modes will obtain larger amplitudes (compared with their stationary counterparts) within the boundary layer. This is due to the fact that the ratio ![]() $N_{t}^{env}/N_{s}^{env}$ only reflects the integrated growth ratio (thus not the amplitude ratio), but does not inform on receptivity or initial amplitudes of these modes. Nonetheless, a primary conclusion can be drawn here regarding the net BFM effect. That is, the net BFM effect weakens both stationary and travelling CFI modes. However, the suppression of stationary CFI modes is more pronounced, thus rendering the boundary layer more susceptible to travelling CFI modes. Additionally, this BFM-caused susceptibility (to travelling CFI modes) is more pronounced at lower
$N_{t}^{env}/N_{s}^{env}$ only reflects the integrated growth ratio (thus not the amplitude ratio), but does not inform on receptivity or initial amplitudes of these modes. Nonetheless, a primary conclusion can be drawn here regarding the net BFM effect. That is, the net BFM effect weakens both stationary and travelling CFI modes. However, the suppression of stationary CFI modes is more pronounced, thus rendering the boundary layer more susceptible to travelling CFI modes. Additionally, this BFM-caused susceptibility (to travelling CFI modes) is more pronounced at lower ![]() $Re$, as implied by the larger increase of
$Re$, as implied by the larger increase of ![]() $N_{t}^{env}/N_{s}^{env}$ at lower
$N_{t}^{env}/N_{s}^{env}$ at lower ![]() $Re$ (figure 6c). This can probably be attributed to the larger forcing authority of PA at lower
$Re$ (figure 6c). This can probably be attributed to the larger forcing authority of PA at lower ![]() $Re$. This assumption is further evaluated by considering an additional case of
$Re$. This assumption is further evaluated by considering an additional case of ![]() $V_{p-p}=9\,{\rm kV}$ and
$V_{p-p}=9\,{\rm kV}$ and ![]() $Re=2.5\times 10^6$, which exhibits a stronger body force than the case of
$Re=2.5\times 10^6$, which exhibits a stronger body force than the case of ![]() $V_{p-p}=7\,{\rm kV}$ and
$V_{p-p}=7\,{\rm kV}$ and ![]() $Re=2.5\times 10^6$. The result is shown by the cyan line in figure 6(c). The BFM-caused susceptibility (to travelling CFI modes) becomes more pronounced in conditions where the PA forcing shows a larger authority (i.e. lower
$Re=2.5\times 10^6$. The result is shown by the cyan line in figure 6(c). The BFM-caused susceptibility (to travelling CFI modes) becomes more pronounced in conditions where the PA forcing shows a larger authority (i.e. lower ![]() $Re$ or larger PA forcing). This observation suggests the possibility that the boundary layer susceptibility to travelling modes is related to the actual magnitude of the boundary layer CF component. This notion arises due the fact that lower
$Re$ or larger PA forcing). This observation suggests the possibility that the boundary layer susceptibility to travelling modes is related to the actual magnitude of the boundary layer CF component. This notion arises due the fact that lower ![]() $Re$ and larger PA forcing essentially refer to scenarios of weaker CF components. However, it is important to underscore that there is currently insufficient evidence to confirm or refute this assumption, highlighting the need for dedicated investigations.
$Re$ and larger PA forcing essentially refer to scenarios of weaker CF components. However, it is important to underscore that there is currently insufficient evidence to confirm or refute this assumption, highlighting the need for dedicated investigations.
4. Effects of plasma-based BFM on CFIs
In this section, the described PA is installed and operated on the ![]() $M3J$ wing towards enabling BFM control at various
$M3J$ wing towards enabling BFM control at various ![]() $Re$ conditions. The boundary layer stability is conditioned using distributed or discrete roughness near the leading edge, corresponding to cases DRP, DRE-A, DRE-B and DRE-C, respectively (table 2). Roughness conditioning is used to enhance stationary CFI modes under conditions of both plasma-off and plasma-on. Flow velocity fields are quantified by planar PIV measurements in the
$Re$ conditions. The boundary layer stability is conditioned using distributed or discrete roughness near the leading edge, corresponding to cases DRP, DRE-A, DRE-B and DRE-C, respectively (table 2). Roughness conditioning is used to enhance stationary CFI modes under conditions of both plasma-off and plasma-on. Flow velocity fields are quantified by planar PIV measurements in the ![]() $yz$ plane at
$yz$ plane at ![]() $x/c_{x}=0.175$. The following analysis aims at describing the influence of plasma-based BFM on both stationary and travelling CFIs.
$x/c_{x}=0.175$. The following analysis aims at describing the influence of plasma-based BFM on both stationary and travelling CFIs.
4.1. Stationary CFIs
Figure 7(a) illustrates the time-average velocity field ![]() $\bar {w}$ (contour) and spanwise gradient
$\bar {w}$ (contour) and spanwise gradient ![]() $\partial \bar {w} /\partial \bar {z}$ (colour) in the case of
$\partial \bar {w} /\partial \bar {z}$ (colour) in the case of ![]() $Re=2.5\times 10^{6}$. Among all tested cases, DRP induces the least significant stationary flow perturbation, presenting a scenario of weakly amplified stationary CFI modes. In contrast, the mean flow fields of all DRE cases show evident spanwise-periodic modulations, presenting scenarios where stationary CFI modes are significantly enhanced. Among all the DRE cases, DRE-A produces considerably more amplified and coherent stationary vortices. This is in agreement with the preliminary LST predictions which suggest that stationary CFI modes of smaller
$Re=2.5\times 10^{6}$. Among all tested cases, DRP induces the least significant stationary flow perturbation, presenting a scenario of weakly amplified stationary CFI modes. In contrast, the mean flow fields of all DRE cases show evident spanwise-periodic modulations, presenting scenarios where stationary CFI modes are significantly enhanced. Among all the DRE cases, DRE-A produces considerably more amplified and coherent stationary vortices. This is in agreement with the preliminary LST predictions which suggest that stationary CFI modes of smaller ![]() $\lambda$ obtain larger
$\lambda$ obtain larger ![]() $N$ factors in the vicinity of the leading edge.
$N$ factors in the vicinity of the leading edge.

Figure 7. Spanwise gradient ![]() $\partial \bar {w}/\partial \bar {z}$ (colour) at (a)
$\partial \bar {w}/\partial \bar {z}$ (colour) at (a) ![]() $Re=2.5\times 10^{6}$ and (b)
$Re=2.5\times 10^{6}$ and (b) ![]() $Re=3.7\times 10^{6}$. Measurements are taken for DRP, DRE-A, DRE-B and DRE-C (columns from left to right) at
$Re=3.7\times 10^{6}$. Measurements are taken for DRP, DRE-A, DRE-B and DRE-C (columns from left to right) at ![]() $x/c_{x}= 0.175$. Black iso-lines illustrate the time-average velocity
$x/c_{x}= 0.175$. Black iso-lines illustrate the time-average velocity ![]() $\bar {w}$, five levels from 0 to 0.7.
$\bar {w}$, five levels from 0 to 0.7.
In all DRE cases the flow fields undergo evident changes when the PA starts working. Noticeably, the PA operation shifts the location of stationary CF vortices towards the ![]() $+z$ direction (i.e. more aligned with the outer inviscid streamlines). This spanwise shift of CF vortices appears as a typical outcome of the BFM strategy, attributed to the localised reduction of the CF component (Peng et al. Reference Peng, Arkesteijn, Avallone and Kotsonis2022a). More importantly, the local maximum and minimum of the spanwise velocity gradient
$+z$ direction (i.e. more aligned with the outer inviscid streamlines). This spanwise shift of CF vortices appears as a typical outcome of the BFM strategy, attributed to the localised reduction of the CF component (Peng et al. Reference Peng, Arkesteijn, Avallone and Kotsonis2022a). More importantly, the local maximum and minimum of the spanwise velocity gradient ![]() $\partial \bar {w}/\partial \bar {z}$ are significantly weakened by the PA forcing, indicating a weakening of the stationary CF vortices. Similar observations are also found for cases at higher
$\partial \bar {w}/\partial \bar {z}$ are significantly weakened by the PA forcing, indicating a weakening of the stationary CF vortices. Similar observations are also found for cases at higher ![]() $Re=3.7\times 10^6$ (figure 7b). Alternatively, the reduction of stationary CFI modes is demonstrated and reflected by the degradation of stationary mode shape. The stationary mode shape is calculated as the spanwise standard deviation of
$Re=3.7\times 10^6$ (figure 7b). Alternatively, the reduction of stationary CFI modes is demonstrated and reflected by the degradation of stationary mode shape. The stationary mode shape is calculated as the spanwise standard deviation of ![]() $w$ and denoted as
$w$ and denoted as ![]() $\langle w \rangle _z$. The mode shape profiles are illustrated in figure 8 at
$\langle w \rangle _z$. The mode shape profiles are illustrated in figure 8 at ![]() $Re=2.5\times 10^6$ and
$Re=2.5\times 10^6$ and ![]() $Re=3.7\times 10^6$. As expected, the spanwise modulation of stationary modes is integrally weakened by the PA forcing. In addition, the secondary hump on the perturbation profiles (denoted by the circular marker) is modified by the PA as well. This secondary hump is related to the characteristic lobe structure of stationary CFIs, which coincides with the advent of nonlinear interactions (Haynes & Reed Reference Haynes and Reed2000; White & Saric Reference White and Saric2005). In terms of the lowest-
$Re=3.7\times 10^6$. As expected, the spanwise modulation of stationary modes is integrally weakened by the PA forcing. In addition, the secondary hump on the perturbation profiles (denoted by the circular marker) is modified by the PA as well. This secondary hump is related to the characteristic lobe structure of stationary CFIs, which coincides with the advent of nonlinear interactions (Haynes & Reed Reference Haynes and Reed2000; White & Saric Reference White and Saric2005). In terms of the lowest-![]() $Re$ cases (figure 8a), the secondary hump only occurs in DRE-A under the condition of plasma-off. This result indicates that stationary CFI modes of DRE-A develop fastest thus first reaching the nonlinear stage, demonstrating the importance of stationary mode receptivity. Considering that the lobe structure is commonly associated with stationary mode saturation and onset of secondary CFIs (Serpieri & Kotsonis Reference Serpieri and Kotsonis2016), the PA forcing appears to retard the evolution of stationary CFI modes.
$Re$ cases (figure 8a), the secondary hump only occurs in DRE-A under the condition of plasma-off. This result indicates that stationary CFI modes of DRE-A develop fastest thus first reaching the nonlinear stage, demonstrating the importance of stationary mode receptivity. Considering that the lobe structure is commonly associated with stationary mode saturation and onset of secondary CFIs (Serpieri & Kotsonis Reference Serpieri and Kotsonis2016), the PA forcing appears to retard the evolution of stationary CFI modes.

Figure 8. Standard deviation profiles of ![]() $\langle w \rangle _{z}$ at (a)
$\langle w \rangle _{z}$ at (a) ![]() $Re=2.5 \times 10^{6}$ and (b)
$Re=2.5 \times 10^{6}$ and (b) ![]() $Re=3.7 \times 10^{6}$.
$Re=3.7 \times 10^{6}$.
To better isolate the forced stationary CFI modes, the spanwise periodicity of the mean flow is leveraged through a spatial fast Fourier transform of the time-average velocity fields. Representative spatial spectra at ![]() $Re=2.5\times 10^{6}$ are illustrated in figure 9. For plasma-off, no significant spectral energy is observed in DRP while the
$Re=2.5\times 10^{6}$ are illustrated in figure 9. For plasma-off, no significant spectral energy is observed in DRP while the ![]() $\bar {\lambda }_6$ and
$\bar {\lambda }_6$ and ![]() $\bar {\lambda }_8$ modes are evidently amplified in DRE-A and DRE-B, along with their harmonic modes. In spite of the successful excitation of stationary CFI modes corresponding to
$\bar {\lambda }_8$ modes are evidently amplified in DRE-A and DRE-B, along with their harmonic modes. In spite of the successful excitation of stationary CFI modes corresponding to ![]() $\lambda _{DRE}$ in DRE-A and DRE-B, the opposite is observed in DRE-C. Instead of the
$\lambda _{DRE}$ in DRE-A and DRE-B, the opposite is observed in DRE-C. Instead of the ![]() $\bar {\lambda }_{10}$ mode, the
$\bar {\lambda }_{10}$ mode, the ![]() $\bar {\lambda }_6$ mode is most enhanced by DRE-C, though weaker than that found in DRE-A. Additionally, multiple spectral modes are amplified which are not necessarily related to
$\bar {\lambda }_6$ mode is most enhanced by DRE-C, though weaker than that found in DRE-A. Additionally, multiple spectral modes are amplified which are not necessarily related to ![]() $\bar {\lambda }_{10}$ or its harmonics. The apparent inability of configuration DRE-C to trigger the respective wavelength of CFIs should be attributed to the fact that the
$\bar {\lambda }_{10}$ or its harmonics. The apparent inability of configuration DRE-C to trigger the respective wavelength of CFIs should be attributed to the fact that the ![]() $\bar {\lambda }_{6}$ mode is significantly more unstable than the
$\bar {\lambda }_{6}$ mode is significantly more unstable than the ![]() $\bar {\lambda }_{10}$ mode at the upstream region of DRE forcing, as indicated by the LST results (figure 5). Notwithstanding, when the PA is on, these DRE-induced spectral modes including their harmonics are evidently inhibited. In contrast, the plasma forcing appears to increase the amplitude of stationary CFIs in the DRP case.
$\bar {\lambda }_{10}$ mode at the upstream region of DRE forcing, as indicated by the LST results (figure 5). Notwithstanding, when the PA is on, these DRE-induced spectral modes including their harmonics are evidently inhibited. In contrast, the plasma forcing appears to increase the amplitude of stationary CFIs in the DRP case.

Figure 9. Non-dimensional spectral amplitude ![]() $\bar {A}(\bar {\lambda })$ for (a) plasma-off and (b) plasma-on at
$\bar {A}(\bar {\lambda })$ for (a) plasma-off and (b) plasma-on at ![]() $Re= 2.5\times 10^{6}$. Black filled triangle,
$Re= 2.5\times 10^{6}$. Black filled triangle, ![]() $\bar {\lambda }=50\ (\lambda =6\,{\rm mm})$; black open triangle,
$\bar {\lambda }=50\ (\lambda =6\,{\rm mm})$; black open triangle, ![]() $\bar {\lambda }=25\ (\lambda =3\,{\rm mm})$; red filled triangle,
$\bar {\lambda }=25\ (\lambda =3\,{\rm mm})$; red filled triangle, ![]() $\bar {\lambda }=66.67\ (\lambda =8\,{\rm mm})$; red open triangle,
$\bar {\lambda }=66.67\ (\lambda =8\,{\rm mm})$; red open triangle, ![]() $\bar {\lambda }=33.33\ (\lambda =4\,{\rm mm})$; blue filled triangle,
$\bar {\lambda }=33.33\ (\lambda =4\,{\rm mm})$; blue filled triangle, ![]() $\bar {\lambda }=83.33$
$\bar {\lambda }=83.33$ ![]() $(\lambda =10\,{\rm mm})$.
$(\lambda =10\,{\rm mm})$.
The spanwise wavelength spectra are further used to quantify the integral amplitude of stationary CFI modes. Specifically, the spectral energy of discrete Fourier modes is integrated from ![]() $\bar {y}_{min}$ to
$\bar {y}_{min}$ to ![]() $\bar {y}=25$ (i.e.
$\bar {y}=25$ (i.e. ![]() $y=3\,{\rm mm}$) and denoted as
$y=3\,{\rm mm}$) and denoted as ![]() $\bar {A}_s(\bar {\lambda })$. Peaks at
$\bar {A}_s(\bar {\lambda })$. Peaks at ![]() $\bar {\lambda }_{10}$,
$\bar {\lambda }_{10}$, ![]() $\bar {\lambda }_6$,
$\bar {\lambda }_6$, ![]() $\bar {\lambda }_8$ and
$\bar {\lambda }_8$ and ![]() $\bar {\lambda }_6$ are chosen as the dominant spectral modes for DRP, DRE-A, DRE-B and DRE-C, respectively. The results are illustrated in figure 10 at various
$\bar {\lambda }_6$ are chosen as the dominant spectral modes for DRP, DRE-A, DRE-B and DRE-C, respectively. The results are illustrated in figure 10 at various ![]() $Re$. Overall, the plasma-based BFM leads to a suppression of stationary CFI modes for all DRE cases as also observed by Peng et al. (Reference Peng, Arkesteijn, Avallone and Kotsonis2022a). It is noticed that the modes around
$Re$. Overall, the plasma-based BFM leads to a suppression of stationary CFI modes for all DRE cases as also observed by Peng et al. (Reference Peng, Arkesteijn, Avallone and Kotsonis2022a). It is noticed that the modes around ![]() $\bar {\lambda }_{10}$ in DRP are slightly enhanced at lower
$\bar {\lambda }_{10}$ in DRP are slightly enhanced at lower ![]() $Re$ though further reduced with increasing
$Re$ though further reduced with increasing ![]() $Re$. Though the origin of this amplification cannot be conclusively determined here, the slow variance or modulation of PA discharge along the spanwise direction appears as a potential cause, which can result from the possible misalignment in PA fabrication and placement. Nonetheless, these additional modes are expected to have insignificant effects on the transition dynamics due to their weak amplitudes. This holds particularly true for DRP cases at higher
$Re$. Though the origin of this amplification cannot be conclusively determined here, the slow variance or modulation of PA discharge along the spanwise direction appears as a potential cause, which can result from the possible misalignment in PA fabrication and placement. Nonetheless, these additional modes are expected to have insignificant effects on the transition dynamics due to their weak amplitudes. This holds particularly true for DRP cases at higher ![]() $Re$ and DRE cases where these additional modes are effectively suppressed by the strong dominant modes induced by the DREs.
$Re$ and DRE cases where these additional modes are effectively suppressed by the strong dominant modes induced by the DREs.

Figure 10. Non-dimensional amplitude ![]() $\bar {A}_{s}(\bar {\lambda })$ of dominant spectral modes for (a) DRP, (b) DRE-A, (c) DRE-B and (d) DRE-C.
$\bar {A}_{s}(\bar {\lambda })$ of dominant spectral modes for (a) DRP, (b) DRE-A, (c) DRE-B and (d) DRE-C.
4.2. Travelling CFIs
The amplitude reduction of stationary CFI modes underlines the positive effects of plasma-based BFM on stabilising the boundary layer. Notwithstanding, previous studies of Serpieri et al. (Reference Serpieri, Venkata and Kotsonis2017) and Peng et al. (Reference Peng, Arkesteijn, Avallone and Kotsonis2022a) have shown that the PA operation inevitably induces travelling CFIs in the boundary layer, which might be attributed to quasi-stochastic processes within the PA micro-discharge (Moralev et al. Reference Moralev, Selivonin and Ustinov2019). Furthermore, the previous LST results indicate that the net BFM effect favours the suppression of stationary over travelling CFI modes, essentially rendering the boundary layer more susceptible to travelling CFIs. In combination, these factors highlight the significance of travelling CFI modes in realistic applications of plasma-based BFM, adding complexity to the successful implementation of this method.
Figure 11 illustrates the unsteady velocity fluctuation ![]() $\langle \bar {w}^{\prime } \rangle$ (colour) overlaid with time-average velocity (contour) at
$\langle \bar {w}^{\prime } \rangle$ (colour) overlaid with time-average velocity (contour) at ![]() $Re=2.5\times 10^{6}$ and
$Re=2.5\times 10^{6}$ and ![]() $Re=3.7\times 10^{6}$. At the condition of
$Re=3.7\times 10^{6}$. At the condition of ![]() $Re=2.5\times 10^{6}$ and plasma-off, unsteady fluctuations already become non-negligible in the near-wall region within the stationary vortex structures. Compared with the DRP case, the unsteady fluctuations are evidently more spanwise-periodic in DRE cases due to the stronger modulation of stationary CFI modes. Among all DRE cases, the intensified unsteady fluctuations are more centralised and compact in DRE-A, corresponding to the highly amplified state of the stationary vortices in this case. Recalling figure 8(a), the level of unsteady fluctuations further demonstrates that the primary CFIs of DRE-A are at a nonlinear stage of growth and subject to a strong mutual interaction at
$Re=2.5\times 10^{6}$ and plasma-off, unsteady fluctuations already become non-negligible in the near-wall region within the stationary vortex structures. Compared with the DRP case, the unsteady fluctuations are evidently more spanwise-periodic in DRE cases due to the stronger modulation of stationary CFI modes. Among all DRE cases, the intensified unsteady fluctuations are more centralised and compact in DRE-A, corresponding to the highly amplified state of the stationary vortices in this case. Recalling figure 8(a), the level of unsteady fluctuations further demonstrates that the primary CFIs of DRE-A are at a nonlinear stage of growth and subject to a strong mutual interaction at ![]() $Re=2.5\times 10^{6}$ and
$Re=2.5\times 10^{6}$ and ![]() $x/c_{x}=0.175$. In contrast, the primary CFIs in DRE-B and DRE-C cases reveal a weaker mutual interaction. When the PA is on, the plasma forcing evidently amplifies unsteady fluctuations in the DRP case, resulting in a boundary layer significantly contaminated by travelling CFIs. In contrast, the PA forcing appears to only marginally affect the DRE cases. In these cases, the spanwise-modulated fluctuations become weaker centrally and tend to spread spatially within stationary structures. Similar results are observed at
$x/c_{x}=0.175$. In contrast, the primary CFIs in DRE-B and DRE-C cases reveal a weaker mutual interaction. When the PA is on, the plasma forcing evidently amplifies unsteady fluctuations in the DRP case, resulting in a boundary layer significantly contaminated by travelling CFIs. In contrast, the PA forcing appears to only marginally affect the DRE cases. In these cases, the spanwise-modulated fluctuations become weaker centrally and tend to spread spatially within stationary structures. Similar results are observed at ![]() $Re=3.7\times 10^{6}$, though the unsteady fluctuations exhibit higher amplitudes and more pronounced modulation in the spanwise direction for both plasma-off and plasma-on.
$Re=3.7\times 10^{6}$, though the unsteady fluctuations exhibit higher amplitudes and more pronounced modulation in the spanwise direction for both plasma-off and plasma-on.

Figure 11. Non-dimensional standard deviation of temporal velocity fluctuation ![]() $\langle \bar {w}^{\prime } \rangle$ for (a)
$\langle \bar {w}^{\prime } \rangle$ for (a) ![]() $Re=2.5\times 10^6$ and (b)
$Re=2.5\times 10^6$ and (b) ![]() $Re=3.7\times 10^6$. The colourbar follows a logarithmic scale.
$Re=3.7\times 10^6$. The colourbar follows a logarithmic scale.
These unsteady fluctuations are mainly amplified in regions of strong spanwise gradients, as shown in figure 7. The spatial locations of these unsteady fluctuations highly resemble the primary type III mode and the secondary type I mode (Wassermann & Kloker Reference Wassermann and Kloker2002). However, these typical fluctuations cannot be conclusively segregated here considering the low acquisition frequency of the utilised PIV measurement technique. Nonetheless, these fluctuations are carefully examined given their intrinsic associations with type III and type I modes, as well as the mutual interactions of primary CFI modes. Hereafter, the fluctuations corresponding to the minimum ![]() $\partial \bar {w}/ \partial \bar {z}$ and the maximum
$\partial \bar {w}/ \partial \bar {z}$ and the maximum ![]() $\partial \bar {w}/ \partial \bar {z}$ are denoted as fluctuation-a and fluctuation-b, as outlined by the red and black lines in figures 7(b) and 11(b). These fluctuation structures are quantified following the method in Peng et al. (Reference Peng, Avallone and Kotsonis2022b), where the fluctuation
$\partial \bar {w}/ \partial \bar {z}$ are denoted as fluctuation-a and fluctuation-b, as outlined by the red and black lines in figures 7(b) and 11(b). These fluctuation structures are quantified following the method in Peng et al. (Reference Peng, Avallone and Kotsonis2022b), where the fluctuation ![]() $\langle \bar {w}^{\prime } \rangle$ is integrated within specific spatial regions (i.e. masks). Specifically, the region of
$\langle \bar {w}^{\prime } \rangle$ is integrated within specific spatial regions (i.e. masks). Specifically, the region of ![]() $\partial \bar {w}/ \partial \bar {z}<-0.5\max (\partial \bar {w}/ \partial \bar {z})$ is used to trace fluctuation-a structure and the region of
$\partial \bar {w}/ \partial \bar {z}<-0.5\max (\partial \bar {w}/ \partial \bar {z})$ is used to trace fluctuation-a structure and the region of ![]() $\partial \bar {w}/ \partial \bar {z}>0.5\max (\partial \bar {w}/ \partial \bar {z})$ for fluctuation-b structure. While the threshold of 0.5 is chosen heuristically, it is kept constant for the entire parameter range, ensuring comparable outcomes. The amplitudes of the two fluctuation structures are ultimately calculated as follows:
$\partial \bar {w}/ \partial \bar {z}>0.5\max (\partial \bar {w}/ \partial \bar {z})$ for fluctuation-b structure. While the threshold of 0.5 is chosen heuristically, it is kept constant for the entire parameter range, ensuring comparable outcomes. The amplitudes of the two fluctuation structures are ultimately calculated as follows:
where ![]() $i=a,b$ and
$i=a,b$ and ![]() $s_m$ denotes the mask area.
$s_m$ denotes the mask area.
The resulting amplitudes ![]() $\bar {A}_a$ and
$\bar {A}_a$ and ![]() $\bar {A}_b$ are illustrated in figures 12(a) and 12(b), respectively. In accordance with the observations in figure 11, the amplitudes of fluctuation-a and fluctuation-b structures are significantly reduced by the PA forcing for all DRP and DRE cases. To facilitate the discussion, the total unsteady fluctuations and stationary CFIs are further quantified. Specifically, the total unsteady fluctuations over the entire domain are quantified as follows: (Downs & White Reference Downs and White2013)
$\bar {A}_b$ are illustrated in figures 12(a) and 12(b), respectively. In accordance with the observations in figure 11, the amplitudes of fluctuation-a and fluctuation-b structures are significantly reduced by the PA forcing for all DRP and DRE cases. To facilitate the discussion, the total unsteady fluctuations and stationary CFIs are further quantified. Specifically, the total unsteady fluctuations over the entire domain are quantified as follows: (Downs & White Reference Downs and White2013)
 \begin{equation} \bar{A}_t= \frac{1}{\delta_{99}-y_{min}}\frac{1}{z_{max}} \int_{0}^{z_{max}}\int_{y_{min}}^{\delta_{99}}\langle \bar{w}^{\prime} \rangle \,{\rm d} z\,{\rm d} y, \end{equation}
\begin{equation} \bar{A}_t= \frac{1}{\delta_{99}-y_{min}}\frac{1}{z_{max}} \int_{0}^{z_{max}}\int_{y_{min}}^{\delta_{99}}\langle \bar{w}^{\prime} \rangle \,{\rm d} z\,{\rm d} y, \end{equation}
where ![]() $z_{max}$ is the spanwise extent of the PIV domain (figure 11) and
$z_{max}$ is the spanwise extent of the PIV domain (figure 11) and ![]() $y_{min}$ is the nearest to the wall position, reliably resolved by the PIV measurement (§ 2.3). The results are summarised in figure 12(c), revealing a general amplification of travelling CFIs due to the PA forcing in all DRP and DRE cases. Though the LST results in § 3 indicate that the net BFM effect essentially weakens both types of CFIs, the impact of intrinsic non-deterministic unsteadiness of the PA forcing results in a relatively more amplified
$y_{min}$ is the nearest to the wall position, reliably resolved by the PIV measurement (§ 2.3). The results are summarised in figure 12(c), revealing a general amplification of travelling CFIs due to the PA forcing in all DRP and DRE cases. Though the LST results in § 3 indicate that the net BFM effect essentially weakens both types of CFIs, the impact of intrinsic non-deterministic unsteadiness of the PA forcing results in a relatively more amplified ![]() $\bar {A}_t$. Additionally, it is not surprising to find that
$\bar {A}_t$. Additionally, it is not surprising to find that ![]() $\bar {A}_t$ displays an opposing tendency compared with
$\bar {A}_t$ displays an opposing tendency compared with ![]() $\bar {A}_a$ and
$\bar {A}_a$ and ![]() $\bar {A}_b$ when the PA is on. This is due to the fact that unsteady fluctuations are mildly amplified by the PA outside of the region of structures a and b (typically evident in DRP cases) and are accumulatively reflected by
$\bar {A}_b$ when the PA is on. This is due to the fact that unsteady fluctuations are mildly amplified by the PA outside of the region of structures a and b (typically evident in DRP cases) and are accumulatively reflected by ![]() $\bar {A}_t$. Furthermore, the amplitudes of total stationary CFI modes
$\bar {A}_t$. Furthermore, the amplitudes of total stationary CFI modes ![]() $\bar {A}_{s}$ are simply calculated as the integral of spanwise standard deviation of
$\bar {A}_{s}$ are simply calculated as the integral of spanwise standard deviation of ![]() $\langle \bar {w} \rangle _{z}$ as follows:
$\langle \bar {w} \rangle _{z}$ as follows:
 \begin{equation} \bar{A}_s=\frac{1}{\delta_{99}-y_{min}}\int_{y_{min}}^{\delta_{99}} \langle \bar{w} \rangle_{z} \,{{\rm d}y} . \end{equation}
\begin{equation} \bar{A}_s=\frac{1}{\delta_{99}-y_{min}}\int_{y_{min}}^{\delta_{99}} \langle \bar{w} \rangle_{z} \,{{\rm d}y} . \end{equation}
The results are shown in figure 12(d). As expected, the amplitudes of total stationary modes agree well with the dominant mode amplitudes ![]() $\bar {A}_s(\bar {\lambda })$ as shown in figure 10, indicating a general reduction of stationary CFI modes due to plasma forcing.
$\bar {A}_s(\bar {\lambda })$ as shown in figure 10, indicating a general reduction of stationary CFI modes due to plasma forcing.

Figure 12. (a) Fluctuation-a amplitude ![]() $\bar {A}_a$. (b) Fluctuation-b amplitude
$\bar {A}_a$. (b) Fluctuation-b amplitude ![]() $\bar {A}_b$. (c) Unsteady fluctuation amplitude
$\bar {A}_b$. (c) Unsteady fluctuation amplitude ![]() $\bar {A}_t$. (d) Stationary CF mode amplitude
$\bar {A}_t$. (d) Stationary CF mode amplitude ![]() $\bar {A}_s$. (e) Ratio
$\bar {A}_s$. (e) Ratio ![]() $\bar {A}_t/\bar {A}_s$. The vertical coordinates follow a logarithmic scale.
$\bar {A}_t/\bar {A}_s$. The vertical coordinates follow a logarithmic scale.
It should be noted that the observed reduction of fluctuation-a and fluctuation-b structures is not contradictory to the observations of Peng et al. (Reference Peng, Arkesteijn, Avallone and Kotsonis2022a), where they were found to be significantly amplified in cases of strongly nonlinear stationary CFIs (i.e. larger ![]() $h_{DRE}$). In fact, the increase of
$h_{DRE}$). In fact, the increase of ![]() $\bar {A}_t$ and the decrease of
$\bar {A}_t$ and the decrease of ![]() $\bar {A}_s$ imply that the reduction of fluctuation-a and fluctuation-b structures can be attributed to the significantly weakened stationary CFI modes. Ultimately, fluctuation-a and fluctuation-b structures tend to depend on the amplitude of their carrying stationary CFI modes remaining downstream of the PA forcing region. This assumption is further supported, considering that stationary CFI modes are significantly weakened by the PA in the present study while remaining almost unaffected in the nonlinear cases of Peng et al. (Reference Peng, Arkesteijn, Avallone and Kotsonis2022a).
$\bar {A}_s$ imply that the reduction of fluctuation-a and fluctuation-b structures can be attributed to the significantly weakened stationary CFI modes. Ultimately, fluctuation-a and fluctuation-b structures tend to depend on the amplitude of their carrying stationary CFI modes remaining downstream of the PA forcing region. This assumption is further supported, considering that stationary CFI modes are significantly weakened by the PA in the present study while remaining almost unaffected in the nonlinear cases of Peng et al. (Reference Peng, Arkesteijn, Avallone and Kotsonis2022a).
Considering the above observations, two primary outcomes governing the response of stationary and travelling CFI modes to the PA forcing can be extracted. The first scenario occurs when the net BFM effect takes dominance, leading to the suppression of both types of CFI modes, as usually found in numerical studies (Dörr & Kloker Reference Dörr and Kloker2015; Guo & Kloker Reference Guo and Kloker2019). Comparatively, the stationary CFI modes tend to be more suppressed in this case, as implied by the LST results. Alternatively, the second scenario arises when the intrinsic non-deterministic unsteadiness of the PA outweighs the net BFM effect, resulting in a significant amplification of travelling CFI modes along with the suppression of stationary CFI modes, as demonstrated in the present study. Notwithstanding, in either scenario, the influences of travelling CFI modes in the boundary layer are expected to be enhanced due to the PA forcing. To estimate such influence, the ratio ![]() $\bar {A}_{t}/\bar {A}_{s}$ is calculated and illustrated in figure 12(e). The ratio
$\bar {A}_{t}/\bar {A}_{s}$ is calculated and illustrated in figure 12(e). The ratio ![]() $\bar {A}_{t}/\bar {A}_{s}$ significantly increases at plasma-on conditions. Nonetheless, it should be noted that this ratio
$\bar {A}_{t}/\bar {A}_{s}$ significantly increases at plasma-on conditions. Nonetheless, it should be noted that this ratio ![]() $\bar {A}_{t}/\bar {A}_{s}$ is a more appropriate metric for linear cases (i.e. cases at relatively low
$\bar {A}_{t}/\bar {A}_{s}$ is a more appropriate metric for linear cases (i.e. cases at relatively low ![]() $Re$) where nonlinear CFI modes (e.g. type III and secondary CFI modes) are not significantly amplified. Furthermore,
$Re$) where nonlinear CFI modes (e.g. type III and secondary CFI modes) are not significantly amplified. Furthermore, ![]() $\bar {A}_{t}/\bar {A}_{s}$ differs significantly from
$\bar {A}_{t}/\bar {A}_{s}$ differs significantly from ![]() $N^{env}_{t}/N^{env}_{s}$ discussed in § 3 and no direct comparison can be drawn at this point.
$N^{env}_{t}/N^{env}_{s}$ discussed in § 3 and no direct comparison can be drawn at this point.
5. Effects of plasma-based BFM on laminar–turbulent transition
This section examines the global effect of plasma-based BFM on the transition topology and location, through the use of IR thermography and corresponding quantification methods described in § 2.4. Several parameters are investigated, including the near-leading-edge surface roughness configurations (i.e. DRP and DRE-A/B/C), wing angle of attack ![]() $\alpha$ and Reynolds number
$\alpha$ and Reynolds number ![]() $Re$.
$Re$.
5.1. Transition topology
Figure 13 illustrates time-average IR images for DRP, DRE-A, DRE-B and DRE-C at ![]() $Re=2.5\times 10^6$. The leading edge of the
$Re=2.5\times 10^6$. The leading edge of the ![]() $M3J$ model is indicated by the white solid line, while the red dashed line indicates the PA location. Additionally, blue dashed lines correspond to constant chord locations
$M3J$ model is indicated by the white solid line, while the red dashed line indicates the PA location. Additionally, blue dashed lines correspond to constant chord locations ![]() $x/c_{x}=0.1$, 0.2, 0.3 and 0.4. For plasma-off, contiguous turbulent wedges appear along the wing span for all tested cases, visualised by the thermal footprint caused by the local breakdown of stationary CF vortices (Saric et al. Reference Saric, Reed and White2003). These wedged transition fronts are also widely observed in swept-wing transition studies (Saric et al. Reference Saric, West, Tufts and Reed2019; Rius-Vidales & Kotsonis Reference Rius-Vidales and Kotsonis2020) and offer a first indication of the dominance of stationary CFIs at plasma-off conditions. In fact, stationary CFI-dominated boundary layers are expected at plasma-off conditions, considering the low level of free-stream turbulence
$x/c_{x}=0.1$, 0.2, 0.3 and 0.4. For plasma-off, contiguous turbulent wedges appear along the wing span for all tested cases, visualised by the thermal footprint caused by the local breakdown of stationary CF vortices (Saric et al. Reference Saric, Reed and White2003). These wedged transition fronts are also widely observed in swept-wing transition studies (Saric et al. Reference Saric, West, Tufts and Reed2019; Rius-Vidales & Kotsonis Reference Rius-Vidales and Kotsonis2020) and offer a first indication of the dominance of stationary CFIs at plasma-off conditions. In fact, stationary CFI-dominated boundary layers are expected at plasma-off conditions, considering the low level of free-stream turbulence ![]() $T_u$ (
$T_u$ (![]() ${<}0.03\,\%$) in the Low Turbulence Tunnel facility and the sensitivity of stationary CFIs to surface roughness (i.e. DRP or DREs). Nonetheless, these wedged transition topologies feature distinct differences between DRP- and DRE-conditioned cases. Evidently, DREs create more spanwise uniform transition fronts than DRP, due to the former's ability to concentrate perturbation energy in one single instability mode (Saric et al. Reference Saric, Reed and White2003; Zoppini et al. Reference Zoppini, Michelis, Ragni and Kotsonis2023). In contrast, the distributed and broadband nature of DRP results in a more irregular transition pattern.
${<}0.03\,\%$) in the Low Turbulence Tunnel facility and the sensitivity of stationary CFIs to surface roughness (i.e. DRP or DREs). Nonetheless, these wedged transition topologies feature distinct differences between DRP- and DRE-conditioned cases. Evidently, DREs create more spanwise uniform transition fronts than DRP, due to the former's ability to concentrate perturbation energy in one single instability mode (Saric et al. Reference Saric, Reed and White2003; Zoppini et al. Reference Zoppini, Michelis, Ragni and Kotsonis2023). In contrast, the distributed and broadband nature of DRP results in a more irregular transition pattern.

Figure 13. Transition front visualisation at ![]() $\alpha =2.5^{\circ }$ and
$\alpha =2.5^{\circ }$ and ![]() $Re=2.5\times 10^{6}$ for (a) plasma-off and (b) plasma-on. Flow comes from the left and measurements are taken for DRP, DRE-A, DRE-B and DRE-C (columns from left to right).
$Re=2.5\times 10^{6}$ for (a) plasma-off and (b) plasma-on. Flow comes from the left and measurements are taken for DRP, DRE-A, DRE-B and DRE-C (columns from left to right).
The characteristics of stationary CFI modes at plasma-off are further revealed by the spanwise wavelength spectra of IR imaging fields, as illustrated in figure 14(a). These spectra are extracted from images of camera IR-Zoom, imaging a FOV corresponding to the magenta box region in figure 13. The absence of evident spectral modes in the upstream portion of the FOV indicates no single monochromatic stationary CFI mode triggered by DRP, agreeing well with the previous PIV observations. In contrast, evident energy peaks are found at ![]() $\bar {\lambda }_6$ and
$\bar {\lambda }_6$ and ![]() $\bar {\lambda }_8$ respectively for DRE-A and DRE-B, confirming the upstream DRE excitation. Despite the same roughness element height
$\bar {\lambda }_8$ respectively for DRE-A and DRE-B, confirming the upstream DRE excitation. Despite the same roughness element height ![]() $h_{DRE}$ of DRE-A and DRE-B (i.e. similar initial amplitudes of
$h_{DRE}$ of DRE-A and DRE-B (i.e. similar initial amplitudes of ![]() $\bar {\lambda }_6$ and
$\bar {\lambda }_6$ and ![]() $\bar {\lambda }_8$ modes), the stationary CF mode of
$\bar {\lambda }_8$ modes), the stationary CF mode of ![]() $\bar {\lambda }_6$ shows an earlier growth than that of
$\bar {\lambda }_6$ shows an earlier growth than that of ![]() $\bar {\lambda }_8$ at both low and high
$\bar {\lambda }_8$ at both low and high ![]() $Re$. This is also in agreement with the LST prediction, namely stationary modes of smaller wavelength are more amplified in the upstream region of the flow. Consistent with the PIV observations, instead of the
$Re$. This is also in agreement with the LST prediction, namely stationary modes of smaller wavelength are more amplified in the upstream region of the flow. Consistent with the PIV observations, instead of the ![]() $\bar {\lambda }_{10}$ mode, the
$\bar {\lambda }_{10}$ mode, the ![]() $\bar {\lambda }_6$ mode is evidently amplified upstream, indicating the dominance of the
$\bar {\lambda }_6$ mode is evidently amplified upstream, indicating the dominance of the ![]() $\bar {\lambda }_6$ mode in DRE-C, though weaker than those induced by DRE-A. In fact, besides the LST-predicted early amplification of stationary modes of shorter
$\bar {\lambda }_6$ mode in DRE-C, though weaker than those induced by DRE-A. In fact, besides the LST-predicted early amplification of stationary modes of shorter ![]() $\bar {\lambda }$, the triggering of the
$\bar {\lambda }$, the triggering of the ![]() $\bar {\lambda }_6$ mode could be potentially attributed to the distinct neutral point locations of
$\bar {\lambda }_6$ mode could be potentially attributed to the distinct neutral point locations of ![]() $\bar {\lambda }_6$ and
$\bar {\lambda }_6$ and ![]() $\bar {\lambda }_{10}$. As shown in figure 5(b), the neutral point of
$\bar {\lambda }_{10}$. As shown in figure 5(b), the neutral point of ![]() $\bar {\lambda }_{10}$ is significantly downstream from the DRE location (i.e.
$\bar {\lambda }_{10}$ is significantly downstream from the DRE location (i.e. ![]() $x/c_x=0.02$) compared with
$x/c_x=0.02$) compared with ![]() $\bar {\lambda }_{6}$, which may consequently hinder the effective excitation of the
$\bar {\lambda }_{6}$, which may consequently hinder the effective excitation of the ![]() $\bar {\lambda }_{10}$ mode in the DRE-C case.
$\bar {\lambda }_{10}$ mode in the DRE-C case.

Figure 14. Wavelength spectra of the same cases as in figure 13. Blue dashed lines correspond to ![]() $x/c_{x}=0.1$ and 0.2. The black, red and blue triangles indicate wavelengths
$x/c_{x}=0.1$ and 0.2. The black, red and blue triangles indicate wavelengths ![]() $\bar {\lambda }_6$,
$\bar {\lambda }_6$, ![]() $\bar {\lambda }_8$ and
$\bar {\lambda }_8$ and ![]() $\bar {\lambda }_{10}$, respectively.
$\bar {\lambda }_{10}$, respectively.
Figure 14(b) presents the wavelength spectra for plasma-on. The spectra demonstrate that the PA forcing weakens the DRE-induced spectral peaks, confirming the general effect of plasma-based BFM in attenuating stationary CFI modes and agreeing well with previous PIV results. Despite the presence of weaker stationary CFI modes in plasma-on scenarios, the ensuing transition front is expected to be topologically similar to that of the plasma-off case (i.e. sharp transition front), as long as stationary CFI modes are still dominant. However, a noticeable change in transition front topology is shown in figure 13(b) and indicates that plasma-based BFM does more than just weakening stationary CFI modes. Compared with plasma-off cases, the PA operation imposes a ‘blurring’ effect on the transition front, where distinct turbulent wedges are spatially spread or even eradicated. This distinct blurred transition front is commonly attributed to the rise of travelling CFI modes and their subsequent unsteady laminar breakdown (Downs & White Reference Downs and White2013). Unlike stationary CFI modes that predominantly propagate along local streamlines, travelling CFI modes exhibit significant deviations in the propagation direction with respect to local streamlines. This observation indicates the enhanced involvement of travelling CFI modes in the boundary layer development and transition process, due to the PA operation.
Following the method introduced in § 2.4, the IR intensity gradient density ![]() $|\boldsymbol {\nabla } I|_{d}$ is used to quantify the blurriness of the transition front, as illustrated in figure 15. Additionally, the ratio
$|\boldsymbol {\nabla } I|_{d}$ is used to quantify the blurriness of the transition front, as illustrated in figure 15. Additionally, the ratio ![]() $c_{I}$ defined as
$c_{I}$ defined as ![]() $(|\boldsymbol {\nabla } I|_{d,off}-|\boldsymbol {\nabla } I|_{d,on})/|\boldsymbol {\nabla } I|_{d,off}$ is calculated to asses the degree of blurring effects and is illustrated in red. Regarding all plasma-off cases, the density
$(|\boldsymbol {\nabla } I|_{d,off}-|\boldsymbol {\nabla } I|_{d,on})/|\boldsymbol {\nabla } I|_{d,off}$ is calculated to asses the degree of blurring effects and is illustrated in red. Regarding all plasma-off cases, the density ![]() $|\boldsymbol {\nabla } I|_{d}$ reaches the minimum for DRE-A at
$|\boldsymbol {\nabla } I|_{d}$ reaches the minimum for DRE-A at ![]() $Re=2.5\times 10^{6}$. This result actually coincides with the slightly contaminated transition topology of DRE-A observed in figure 13(a), implying a relatively weak stationary CFI-dominated transition. When the PA is on, the transition front is significantly affected. As shown in figure 15,
$Re=2.5\times 10^{6}$. This result actually coincides with the slightly contaminated transition topology of DRE-A observed in figure 13(a), implying a relatively weak stationary CFI-dominated transition. When the PA is on, the transition front is significantly affected. As shown in figure 15, ![]() $|\boldsymbol {\nabla } I|_{d}$ generally presents very low values at plasma-on (especially at lower
$|\boldsymbol {\nabla } I|_{d}$ generally presents very low values at plasma-on (especially at lower ![]() $Re$), indicating contaminated transition fronts following the PA forcing. Furthermore, the tendency of
$Re$), indicating contaminated transition fronts following the PA forcing. Furthermore, the tendency of ![]() $|\boldsymbol {\nabla } I|_{d}$ also agrees well with the envelope ratio
$|\boldsymbol {\nabla } I|_{d}$ also agrees well with the envelope ratio ![]() $N^{env}_t/N^{env}_s$ found in § 3 and the ratio
$N^{env}_t/N^{env}_s$ found in § 3 and the ratio ![]() $\bar {A}_t/\bar {A}_s$ in § 4.2, which obtain larger values at plasma-on conditions. The observations ultimately lead to the conclusion that the PA operation significantly expands the involvement of travelling CFI modes in the boundary layer and diminishes the dominance of stationary CFI modes. On the other hand, it is noticed that
$\bar {A}_t/\bar {A}_s$ in § 4.2, which obtain larger values at plasma-on conditions. The observations ultimately lead to the conclusion that the PA operation significantly expands the involvement of travelling CFI modes in the boundary layer and diminishes the dominance of stationary CFI modes. On the other hand, it is noticed that ![]() $|\boldsymbol {\nabla } I|_{d}$ generally obtains larger values at higher
$|\boldsymbol {\nabla } I|_{d}$ generally obtains larger values at higher ![]() $Re$ at both plasma-off and on. Such result also coincides with the observation of
$Re$ at both plasma-off and on. Such result also coincides with the observation of ![]() $N^{env}_t/N^{env}_s$ (figure 6c), where
$N^{env}_t/N^{env}_s$ (figure 6c), where ![]() $N^{env}_t/N^{env}_s$ generally exhibits smaller values at higher
$N^{env}_t/N^{env}_s$ generally exhibits smaller values at higher ![]() $Re$. This reveals a dependence of blurriness of transition on
$Re$. This reveals a dependence of blurriness of transition on ![]() $Re$. Specifically, the transition front will be less blurred (i.e. less contaminated by travelling CFI modes/more dominated by stationary CFI modes) at higher
$Re$. Specifically, the transition front will be less blurred (i.e. less contaminated by travelling CFI modes/more dominated by stationary CFI modes) at higher ![]() $Re$. This is also supported by the trend of
$Re$. This is also supported by the trend of ![]() $c_I$ observed in figure 15. Generally,
$c_I$ observed in figure 15. Generally, ![]() $c_{I}$ exhibits higher values at lower
$c_{I}$ exhibits higher values at lower ![]() $Re$ and lower values at higher
$Re$ and lower values at higher ![]() $Re$. In other words, the PA exerts a more pronounced blurring effect on the transition front at lower
$Re$. In other words, the PA exerts a more pronounced blurring effect on the transition front at lower ![]() $Re$, suggesting that travelling CFI modes are more likely to dominate the transition at these conditions.
$Re$, suggesting that travelling CFI modes are more likely to dominate the transition at these conditions.

Figure 15. Average IR intensity gradient density ![]() $|\boldsymbol {\nabla } I|_{d}$ and ratio
$|\boldsymbol {\nabla } I|_{d}$ and ratio ![]() $c_I$ at various
$c_I$ at various ![]() $Re$ (
$Re$ (![]() $\alpha =2.5^{\circ }$) for (a) DRP, (b) DRE-A, (c) DRE-B and (d) DRE-C. The dot-dashed line indicates
$\alpha =2.5^{\circ }$) for (a) DRP, (b) DRE-A, (c) DRE-B and (d) DRE-C. The dot-dashed line indicates ![]() $|\boldsymbol {\nabla } I|_{d}$ of DRE-A at
$|\boldsymbol {\nabla } I|_{d}$ of DRE-A at ![]() $Re=2.5\times 10^{6}$ and plasma-off.
$Re=2.5\times 10^{6}$ and plasma-off.
5.2. Transition location
Following the approach described in § 2.4, the net laminar gain is quantified and transformed to an equivalent transition shift ![]() $\Delta (x_{t}/c_{x})$, where
$\Delta (x_{t}/c_{x})$, where ![]() $\Delta (x_{t}/c_{x})>0$ refers to the transition delay and vice versa. The results are illustrated in figure 16 for various
$\Delta (x_{t}/c_{x})>0$ refers to the transition delay and vice versa. The results are illustrated in figure 16 for various ![]() $Re$ and
$Re$ and ![]() $\alpha$. In the case of DRP, the PA evidently advances the transition, particularly at lower
$\alpha$. In the case of DRP, the PA evidently advances the transition, particularly at lower ![]() $\alpha$ and lower
$\alpha$ and lower ![]() $Re$. This result agrees well with the previous observation of
$Re$. This result agrees well with the previous observation of ![]() $|\boldsymbol {\nabla } I|_{d}$ suggesting a transition scenario dominated by travelling CFIs (as evident by the blurred transition front) at lower
$|\boldsymbol {\nabla } I|_{d}$ suggesting a transition scenario dominated by travelling CFIs (as evident by the blurred transition front) at lower ![]() $Re$. It is reasonable to assume that the higher efficacy of the PA in advancing transition at lower
$Re$. It is reasonable to assume that the higher efficacy of the PA in advancing transition at lower ![]() $Re$ is closely linked to the higher susceptibility of the boundary layer to travelling CFI modes. This is supported by the more pronounced increase of the envelope ratio
$Re$ is closely linked to the higher susceptibility of the boundary layer to travelling CFI modes. This is supported by the more pronounced increase of the envelope ratio ![]() $N^{env}_t/N^{env}_s$ at lower
$N^{env}_t/N^{env}_s$ at lower ![]() $Re$ under conditions of plasma-on (figure 6c). It is important to emphasise here that the observations regarding the DRP case do not contradict the fundamental concept of plasma-based BFM. The latter is meant to yield transition delay, especially at lower
$Re$ under conditions of plasma-on (figure 6c). It is important to emphasise here that the observations regarding the DRP case do not contradict the fundamental concept of plasma-based BFM. The latter is meant to yield transition delay, especially at lower ![]() $Re$ where a given PA attains greater control authority within the boundary layer. Based on previous observations, the significant transition-advance effect is instead attributed to the competition between net BFM effect and intrinsic PA unsteadiness, as briefly described below. In the case of an idealised PA able to provide a time-invariant net BFM effect (as commonly utilised in numerical simulations; Dörr & Kloker Reference Dörr and Kloker2015), the transition is expected to be notably delayed. As
$Re$ where a given PA attains greater control authority within the boundary layer. Based on previous observations, the significant transition-advance effect is instead attributed to the competition between net BFM effect and intrinsic PA unsteadiness, as briefly described below. In the case of an idealised PA able to provide a time-invariant net BFM effect (as commonly utilised in numerical simulations; Dörr & Kloker Reference Dörr and Kloker2015), the transition is expected to be notably delayed. As ![]() $Re$ increases, the transition delay becomes less significant until the PA loses its authority over the bulk boundary layer flow. However, in the case of a realistic PA, due to the intrinsic unsteadiness of the forcing, travelling CFI modes can be triggered and amplified in the boundary layer. On the one hand, these initiated travelling CFI modes are favoured by the boundary layer at low-
$Re$ increases, the transition delay becomes less significant until the PA loses its authority over the bulk boundary layer flow. However, in the case of a realistic PA, due to the intrinsic unsteadiness of the forcing, travelling CFI modes can be triggered and amplified in the boundary layer. On the one hand, these initiated travelling CFI modes are favoured by the boundary layer at low-![]() $Re$ conditions and ultimately cancel out the beneficial net BFM effect, leading to significant transition advance. On the other hand, as
$Re$ conditions and ultimately cancel out the beneficial net BFM effect, leading to significant transition advance. On the other hand, as ![]() $Re$ increases, the effectiveness of the net BFM effect diminishes due to the decreasing authority of the PA, even though the boundary layer becomes less susceptible to travelling modes. It is yet to be determined whether there is an intermediate regime, where these two competing effects result in net transition delay.
$Re$ increases, the effectiveness of the net BFM effect diminishes due to the decreasing authority of the PA, even though the boundary layer becomes less susceptible to travelling modes. It is yet to be determined whether there is an intermediate regime, where these two competing effects result in net transition delay.

Figure 16. Transition front shift ![]() $\Delta (x_{t}/c_{x})$ for various combinations of
$\Delta (x_{t}/c_{x})$ for various combinations of ![]() $Re$ and
$Re$ and ![]() $\alpha$ for (a) DRP, (b) DRE-A, (c) DRE-B and (d) DRE-C.
$\alpha$ for (a) DRP, (b) DRE-A, (c) DRE-B and (d) DRE-C.
In comparison with DRP, DRE-A exhibits similar trends of transition shift ![]() $\Delta (x_{t}/c_{x})$ though with weaker values, indicating weaker PA effects in advancing transition. Nonetheless, it is noticed that
$\Delta (x_{t}/c_{x})$ though with weaker values, indicating weaker PA effects in advancing transition. Nonetheless, it is noticed that ![]() $\Delta (x_{t}/c_{x})$ of DRE-A generally attains larger values at higher
$\Delta (x_{t}/c_{x})$ of DRE-A generally attains larger values at higher ![]() $Re$. This trend is further enhanced at higher angles of attack, where
$Re$. This trend is further enhanced at higher angles of attack, where ![]() $\Delta (x_{t}/c_{x})$ even becomes slightly positive, indicating a subtle yet discernible transition delay. Similar trends can be observed in DRE-B and DRE-C, as shown in figure 16(c,d). However, the impact of the PA on advancing transition is considerably weaker in DRE-B and DRE-C. In contrast, noticeable transition delays occur within a moderate range of
$\Delta (x_{t}/c_{x})$ even becomes slightly positive, indicating a subtle yet discernible transition delay. Similar trends can be observed in DRE-B and DRE-C, as shown in figure 16(c,d). However, the impact of the PA on advancing transition is considerably weaker in DRE-B and DRE-C. In contrast, noticeable transition delays occur within a moderate range of ![]() $Re$ at various
$Re$ at various ![]() $\alpha$. It appears that the weak transition delay observed in DRE-A is enhanced in DRE-B and DRE-C, underscoring the crucial roles of the forced wavelengths
$\alpha$. It appears that the weak transition delay observed in DRE-A is enhanced in DRE-B and DRE-C, underscoring the crucial roles of the forced wavelengths ![]() $\lambda _{DRE}$.
$\lambda _{DRE}$.
The occurrence of the maximum ![]() $\Delta (x_{t}/c_{x})$ in DRE-B and DRE-C exhibits similarities to early studies of Deyhle & Bippes (Reference Deyhle and Bippes1996) and Bippes (Reference Bippes1999). In their studies, transition was delayed when increasing the free-stream turbulence
$\Delta (x_{t}/c_{x})$ in DRE-B and DRE-C exhibits similarities to early studies of Deyhle & Bippes (Reference Deyhle and Bippes1996) and Bippes (Reference Bippes1999). In their studies, transition was delayed when increasing the free-stream turbulence ![]() $T_{u}$ to moderate levels, compared with the extremely low
$T_{u}$ to moderate levels, compared with the extremely low ![]() $T_{u}$. Whereas on further increasing
$T_{u}$. Whereas on further increasing ![]() $T_{u}$ to higher levels, transition was again advanced. The growth and saturation of stationary CFI modes were observed to be suppressed in cases of high
$T_{u}$ to higher levels, transition was again advanced. The growth and saturation of stationary CFI modes were observed to be suppressed in cases of high ![]() $T_u$. As hypothesised by those authors, when
$T_u$. As hypothesised by those authors, when ![]() $T_u$ is low, stationary vortices dominate the boundary layer and their higher saturation leads to strongly amplified secondary CFIs thus lowering the transitional
$T_u$ is low, stationary vortices dominate the boundary layer and their higher saturation leads to strongly amplified secondary CFIs thus lowering the transitional ![]() $Re$. Conversely, higher
$Re$. Conversely, higher ![]() $T_{u}$ stimulates primary travelling CFI modes thus advancing the transition as well. However, in an intermediate range of
$T_{u}$ stimulates primary travelling CFI modes thus advancing the transition as well. However, in an intermediate range of ![]() $T_u$, travelling CFI modes would suppress the growth and saturation of stationary CFI modes while themselves not growing sufficiently to incur breakdown, thereby resulting in a net transition delay. The interaction between primary stationary and travelling CFI modes was further investigated in the numerical work of Malik, Li & Chang (Reference Malik, Li and Chang1994). The results indicate that the intensity of nonlinear interactions between the primary stationary and travelling CFI modes depends on their initial amplitudes. In scenarios where the two primary modes have comparable amplitudes, the growth and saturation of stationary modes are indeed significantly suppressed. Similarly, the numerical work of Guo & Kloker (Reference Guo and Kloker2019) achieved transition delay by enhancing travelling CFI modes to suppress the dominant stationary CFI modes.
$T_u$, travelling CFI modes would suppress the growth and saturation of stationary CFI modes while themselves not growing sufficiently to incur breakdown, thereby resulting in a net transition delay. The interaction between primary stationary and travelling CFI modes was further investigated in the numerical work of Malik, Li & Chang (Reference Malik, Li and Chang1994). The results indicate that the intensity of nonlinear interactions between the primary stationary and travelling CFI modes depends on their initial amplitudes. In scenarios where the two primary modes have comparable amplitudes, the growth and saturation of stationary modes are indeed significantly suppressed. Similarly, the numerical work of Guo & Kloker (Reference Guo and Kloker2019) achieved transition delay by enhancing travelling CFI modes to suppress the dominant stationary CFI modes.
In a similar manner, the current work also observes the suppression of the development and saturation of stationary CFI modes. For each considered DRE case, the amplitudes of ![]() $P(\bar {\lambda })$ are extracted from the spectra in figure 14 and illustrated in figure 17. To be noted is that
$P(\bar {\lambda })$ are extracted from the spectra in figure 14 and illustrated in figure 17. To be noted is that ![]() $P(\bar {\lambda })$ is the IR intensity, which presents the thermal footprint of stationary vortices rather than their actual amplitudes. Nonetheless, considering that the IR intensity (i.e. surface temperature difference) arises from the shear stress generated by these vortices,
$P(\bar {\lambda })$ is the IR intensity, which presents the thermal footprint of stationary vortices rather than their actual amplitudes. Nonetheless, considering that the IR intensity (i.e. surface temperature difference) arises from the shear stress generated by these vortices, ![]() $P(\bar {\lambda })$ can indirectly (albeit not linearly proportional) reflect the strength of stationary CFI modes. Evidently, in all tested cases, the growth and saturation of dominant stationary modes are generally suppressed due to the PA forcing. While this suppression effect may initially appear to be related to plasma-induced travelling CFI modes, it is important to take the net BFM effect into consideration as well. As demonstrated by previous results, the net BFM effect essentially renders the boundary layer more susceptible to travelling CFI modes, which could indirectly contribute to the suppression of stationary CFI modes’ saturation. In the context of the current work, it remains challenging to conclusively identify whether the suppression of stationary CFI modes is primarily attributed to the plasma-induced travelling CFI modes, the net BFM effect, or a combination of both factors.
$P(\bar {\lambda })$ can indirectly (albeit not linearly proportional) reflect the strength of stationary CFI modes. Evidently, in all tested cases, the growth and saturation of dominant stationary modes are generally suppressed due to the PA forcing. While this suppression effect may initially appear to be related to plasma-induced travelling CFI modes, it is important to take the net BFM effect into consideration as well. As demonstrated by previous results, the net BFM effect essentially renders the boundary layer more susceptible to travelling CFI modes, which could indirectly contribute to the suppression of stationary CFI modes’ saturation. In the context of the current work, it remains challenging to conclusively identify whether the suppression of stationary CFI modes is primarily attributed to the plasma-induced travelling CFI modes, the net BFM effect, or a combination of both factors.

Figure 17. Spectral amplitudes ![]() $P(\bar {\lambda })$ extracted from the wavelength spectra (as shown in figure 14) at (a)
$P(\bar {\lambda })$ extracted from the wavelength spectra (as shown in figure 14) at (a) ![]() $\bar {\lambda }_6$ in DRE-A, (b)
$\bar {\lambda }_6$ in DRE-A, (b) ![]() $\bar {\lambda }_8$ in DRE-B and (c)
$\bar {\lambda }_8$ in DRE-B and (c) ![]() $\bar {\lambda }_6$ in DRE-C.
$\bar {\lambda }_6$ in DRE-C.
In summary, the dependence of the transition behaviour on plasma-based BFM is found to follow trends analogous to free-stream turbulence (Deyhle & Bippes Reference Deyhle and Bippes1996; Bippes Reference Bippes1999). At the ![]() $Re$ and
$Re$ and ![]() $\alpha$ conditions where transition delay is maximised, the plasma-induced travelling CFI modes are likely to suppress the stationary CFI modes while themselves not growing excessively. This assumption is further supported by the moderate values of
$\alpha$ conditions where transition delay is maximised, the plasma-induced travelling CFI modes are likely to suppress the stationary CFI modes while themselves not growing excessively. This assumption is further supported by the moderate values of ![]() $|\boldsymbol {\nabla } I|_{d,on}$ (figure 15) and
$|\boldsymbol {\nabla } I|_{d,on}$ (figure 15) and ![]() $\bar {A}_{t,on}/\bar {A}_{s,on}$ (figure 12) in the range of transition delay
$\bar {A}_{t,on}/\bar {A}_{s,on}$ (figure 12) in the range of transition delay ![]() $Re$. This outcome further highlights a major limitation of plasma-based BFM, namely the requirement of sufficiently amplified stationary CFI modes in the boundary layer. This also aligns with the findings of Deyhle & Bippes (Reference Deyhle and Bippes1996), where transition was found to be most delayed in cases of moderate stationary vortices coexisting with travelling CFI modes initiated by a moderate
$Re$. This outcome further highlights a major limitation of plasma-based BFM, namely the requirement of sufficiently amplified stationary CFI modes in the boundary layer. This also aligns with the findings of Deyhle & Bippes (Reference Deyhle and Bippes1996), where transition was found to be most delayed in cases of moderate stationary vortices coexisting with travelling CFI modes initiated by a moderate ![]() $T_u$.
$T_u$.
6. Conclusion
This study employs a DBD PA to control CFIs and transition on a swept-wing model, through the BFM strategy. A typical two-dimensional spanwise-invariant PA is installed near the leading edge (![]() $x/c_{x}=0.035$), forcing against the CF component. The net BFM effect is numerically investigated through a simplified body force model and LST. The results confirm a general stabilisation of both stationary and travelling CFIs due to the CF reduction. However, the ratio
$x/c_{x}=0.035$), forcing against the CF component. The net BFM effect is numerically investigated through a simplified body force model and LST. The results confirm a general stabilisation of both stationary and travelling CFIs due to the CF reduction. However, the ratio ![]() $N^{env}_t/N^{env}_s$ implies that stationary CFI modes are more suppressed by the net BFM effect, rendering the boundary layer more susceptible to travelling CFI modes. This effect is particularly strong at lower Reynolds number and for stronger PA forcing.
$N^{env}_t/N^{env}_s$ implies that stationary CFI modes are more suppressed by the net BFM effect, rendering the boundary layer more susceptible to travelling CFI modes. This effect is particularly strong at lower Reynolds number and for stronger PA forcing.
The effects of plasma-based BFM on stationary and travelling CFIs are experimentally investigated by planar PIV at ![]() $x/c_x=0.175$. Distinct stationary CFI modes are initiated by surface roughness arrays. The dominant stationary CFI modes are weakened by the PA forcing, along with the reduction of spanwise gradient
$x/c_x=0.175$. Distinct stationary CFI modes are initiated by surface roughness arrays. The dominant stationary CFI modes are weakened by the PA forcing, along with the reduction of spanwise gradient ![]() $\partial \bar {w}/\partial z$ and characteristic lobe structures, in agreement with Peng et al. (Reference Peng, Arkesteijn, Avallone and Kotsonis2022a). However, the amplitude ratio
$\partial \bar {w}/\partial z$ and characteristic lobe structures, in agreement with Peng et al. (Reference Peng, Arkesteijn, Avallone and Kotsonis2022a). However, the amplitude ratio ![]() $\bar {A}_t/\bar {A}_s$ further indicates the increase of travelling CFI modes in the boundary layer due to the plasma-based BFM strategy, which is more pronounced at lower Reynolds numbers.
$\bar {A}_t/\bar {A}_s$ further indicates the increase of travelling CFI modes in the boundary layer due to the plasma-based BFM strategy, which is more pronounced at lower Reynolds numbers.
Transition topology and location are inspected through IR thermography. Generally, the average IR intensity gradient density ![]() $|\boldsymbol {\nabla } I|_{d}$ obtains lower values at conditions of plasma-on, demonstrating a blurred transition front due to the contamination from travelling CFIs. Specifically, this contamination is more severe when the PA works at lower Reynolds number. The transition shift
$|\boldsymbol {\nabla } I|_{d}$ obtains lower values at conditions of plasma-on, demonstrating a blurred transition front due to the contamination from travelling CFIs. Specifically, this contamination is more severe when the PA works at lower Reynolds number. The transition shift ![]() $\Delta (x_t/c_x)$ is further investigated with respect to Reynolds number, angle of attack and wavelength of excited stationary CFI modes. In cases of weak stationary CFIs (i.e. when forced by DRP), the PA exhibits a strong ability in advancing transition, especially at lower Reynolds numbers. The transition-advancing effect is weaker in cases of strong stationary CFI modes (i.e. when force by DREs). This outcome follows the observation of Deyhle & Bippes (Reference Deyhle and Bippes1996) and Bippes (Reference Bippes1999) where transition was delayed in a specific range of free-stream turbulence
$\Delta (x_t/c_x)$ is further investigated with respect to Reynolds number, angle of attack and wavelength of excited stationary CFI modes. In cases of weak stationary CFIs (i.e. when forced by DRP), the PA exhibits a strong ability in advancing transition, especially at lower Reynolds numbers. The transition-advancing effect is weaker in cases of strong stationary CFI modes (i.e. when force by DREs). This outcome follows the observation of Deyhle & Bippes (Reference Deyhle and Bippes1996) and Bippes (Reference Bippes1999) where transition was delayed in a specific range of free-stream turbulence ![]() $T_{u}$, outside of which the transition was advanced.
$T_{u}$, outside of which the transition was advanced.
In conclusion, in realistic application conditions, the plasma forcing introduces the theoretically predicted net BFM effect and non-deterministic perturbations into the boundary layer. Both effects essentially enhance travelling CFIs in the boundary layer. Due to their substantial growth, these travelling CFIs can potentially hinder the effectiveness of the net ‘nominal’ BFM effect. The alignment of the current results with previous work suggests that travelling CFIs may possibly have diminished the detrimental impacts of PA forcing or even contribute positively to the net BFM effect by suppressing stationary CFIs, under certain circumstances. However, this cannot be confirmed by the current work and needs further investigations.
Acknowledgements
The authors would like to acknowledge technical support from S. Bernardy and E. Langedijk during the experimental preparation. A dedicated acknowledgement goes to colleagues G. Zoppini and T. Michelis for their contribution and support during this study.
Funding
The first author (K.P.) would like to acknowledge financial support by the China Scholarship Council (CSC). The last author (M.K.) is supported by the European Research Council (ERC), through StG GLOWING (grant number 803082).
Declaration of interests
The authors report no conflict of interest.