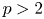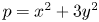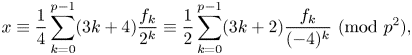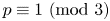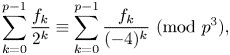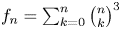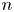1. Introduction
In 1894, Franel [Reference Franel2] found that the numbers

satisfy the recurrence relation (cf. [Reference Sloane14, A000172]):
These numbers are now called Franel numbers. Callan [Reference Callan1] found a combinatorial interpretation of the Franel numbers. The Franel numbers play important roles in combinatorics and number theory. The sequence $\{f_n\}_{n \geqslant 0}$![]() is one of the five sporadic sequences (cf. [Reference Zagier23, § 4]) which are integral solutions of certain Apéry-like recurrence equations and closely related to the theory of modular forms. In 2013, Sun [Reference Sun19] revealed some unexpected connections between the numbers $f_n$
is one of the five sporadic sequences (cf. [Reference Zagier23, § 4]) which are integral solutions of certain Apéry-like recurrence equations and closely related to the theory of modular forms. In 2013, Sun [Reference Sun19] revealed some unexpected connections between the numbers $f_n$![]() and representations of primes $p \equiv 1 (\text{mod} 3)$
and representations of primes $p \equiv 1 (\text{mod} 3)$![]() in the form $x^2+3y^2$
in the form $x^2+3y^2$![]() with $x,y\in \mathbb {Z}$
with $x,y\in \mathbb {Z}$![]() , for example, Sun [Reference Sun19, (1.2)] showed that
, for example, Sun [Reference Sun19, (1.2)] showed that

and in the same paper, Sun proposed some conjectures involving Franel numbers, one of which is
Conjecture 1.1 Let $p>2$![]() be a prime. If $p=x^2+3y^2$
be a prime. If $p=x^2+3y^2$![]() with $x,y\in \mathbb {Z}$
with $x,y\in \mathbb {Z}$![]() and $x\equiv 1 ({\rm {mod}}\ 3)$
and $x\equiv 1 ({\rm {mod}}\ 3)$![]() , then
, then

For more details on Franel numbers, we refer the readers to [Reference Guo3, Reference Guo4, Reference Liu6, Reference Mao8, Reference Mao9, Reference Sun18, Reference Sun20] and so on.
In this paper, our first goal is to prove the above conjecture.
Theorem 1.1 Conjecture 1.1 is true.
Combining (1.1) and theorem 1.1, we immediately obtain the following result.
Corollary 1.1 For any prime $p\equiv 1\pmod 3$![]() , we have
, we have

Sun [Reference Sun19] also gave the following conjecture.
Conjecture 1.2 Let $p>2$![]() be a prime. If $p\equiv 1\pmod 3$
be a prime. If $p\equiv 1\pmod 3$![]() , then
, then

Our last goal is to prove this conjecture.
Theorem 1.2 Conjecture 1.2 is true.
We are going to prove theorem 1.1 in §2. Section 3 is devoted to proving theorem 1.2. Our proofs make use of some combinatorial identities which were found by the package Sigma [Reference Schneider13] via software Mathematica and the $p$![]() -adic gamma function. The proof of theorem 1.2 is somewhat difficult and complex because it is rather convoluted. Throughout this paper, prime $p$
-adic gamma function. The proof of theorem 1.2 is somewhat difficult and complex because it is rather convoluted. Throughout this paper, prime $p$![]() always $\equiv 1\pmod 3$
always $\equiv 1\pmod 3$![]() , so in the following lemmas $p>5$
, so in the following lemmas $p>5$![]() or $p>3$
or $p>3$![]() or $p>2$
or $p>2$![]() is the same, we mention it here first.
is the same, we mention it here first.
2. Proof of theorem 1.1
For a prime $p$![]() , let $\mathbb {Z}_p$
, let $\mathbb {Z}_p$![]() denote the ring of all $p$
denote the ring of all $p$![]() -adic integers and let $\mathbb {Z}_p^{\times }:=\{a\in \mathbb {Z}_p:\,a\text { is prime to }p\}.$
-adic integers and let $\mathbb {Z}_p^{\times }:=\{a\in \mathbb {Z}_p:\,a\text { is prime to }p\}.$![]() For each $\alpha \in \mathbb {Z}_p$
For each $\alpha \in \mathbb {Z}_p$![]() , define the $p$
, define the $p$![]() -adic order $\nu _p(\alpha ):=\max \{n\in \mathbb {N}:\, p^n\mid \alpha \}$
-adic order $\nu _p(\alpha ):=\max \{n\in \mathbb {N}:\, p^n\mid \alpha \}$![]() and the $p$
and the $p$![]() -adic norm $|\alpha |_p:=p^{-\nu _p(\alpha )}$
-adic norm $|\alpha |_p:=p^{-\nu _p(\alpha )}$![]() . Define the $p$
. Define the $p$![]() -adic gamma function $\Gamma _p(\cdot )$
-adic gamma function $\Gamma _p(\cdot )$![]() by
by

and
In particular, we set $\Gamma _p(0)=1$![]() . In the following, we need to use the most basic properties of $\Gamma _p$
. In the following, we need to use the most basic properties of $\Gamma _p$![]() , and all of them can be found in [Reference Murty11, Reference Robert12]. For example, we know that
, and all of them can be found in [Reference Murty11, Reference Robert12]. For example, we know that

where $a_0(x)\in \{1,2,\ldots,p\}$![]() such that $x\equiv a_0(x)\ ({\rm {mod}}\ p)$
such that $x\equiv a_0(x)\ ({\rm {mod}}\ p)$![]() . And a property we need here is the fact that for any positive integer $n$
. And a property we need here is the fact that for any positive integer $n$![]() ,
,
Lemma 2.1 ([Reference Sun19, lemma 2.2]) For any $n\in \mathbb {N}$![]() we have
we have

and

For $n,m\in \{1,2,3,\ldots \}$![]() , define
, define

these numbers with $m=1$![]() are often called the classic harmonic numbers. Recall that the Bernoulli polynomials are given by
are often called the classic harmonic numbers. Recall that the Bernoulli polynomials are given by

Lemma 2.2 ([Reference Sun15, Reference Sun16]) Let $p>5$![]() be a prime. Then
be a prime. Then

where $q_p(a)=(a^{p-1}-1)/p$![]() stands for the Fermat quotient.
stands for the Fermat quotient.
Lemma 2.3 Let $p>5$![]() be a prime. If $0\leq j\leq (p-1)/2$
be a prime. If $0\leq j\leq (p-1)/2$![]() , then we have
, then we have
Proof. If $0\leq j\leq (p-1)/2$![]() and $j\neq (p-1)/3$
and $j\neq (p-1)/3$![]() , then we have
, then we have

If $j=(p-1)/3$![]() , then by lemma 2.2, we have
, then by lemma 2.2, we have

and
Now the proof of lemma 2.3 is complete.
Proof of theorem 1.1 With the help of (2.4), we have

By loading the package Sigma in software Mathematica, we find the following identity:

Thus, replacing $n$![]() by $p$
by $p$![]() in the above identity and then substitute it into (2.6), we have
in the above identity and then substitute it into (2.6), we have

Hence, we immediately obtain the following result by lemma 2.3,

It is easy to verify that

where

and
Applying the famous partial fraction identity

with $x=1/3, n=(p-1)/2$![]() and $x=2/3,n=(p-1)/2$
and $x=2/3,n=(p-1)/2$![]() , we may simplify (2.9) as
, we may simplify (2.9) as
where $(a)_n=a(a+1)\cdots (a+n-1)$![]() is the rising factorial or the Pochhammer symbol.
is the rising factorial or the Pochhammer symbol.
In view of (2.2), we have

where $\Gamma (\cdot )$![]() is the gamma function. In view of [Reference Long and Ramakrishna7, theorem 14] and [Reference Liu5, (2.4)] (or [Reference Mao and Pan10, (3.2)]), for $\alpha,s\in \mathbb {Z}_p$
is the gamma function. In view of [Reference Long and Ramakrishna7, theorem 14] and [Reference Liu5, (2.4)] (or [Reference Mao and Pan10, (3.2)]), for $\alpha,s\in \mathbb {Z}_p$![]() , we have
, we have
and

where $\Gamma _p'(x)$![]() denotes the $p$
denotes the $p$![]() -adic derivative of $\Gamma _p(x)$
-adic derivative of $\Gamma _p(x)$![]() , $\langle \alpha \rangle _n$
, $\langle \alpha \rangle _n$![]() denotes the least non-negative residue of $\alpha$
denotes the least non-negative residue of $\alpha$![]() modulo $n$
modulo $n$![]() , i.e. the integer lying in $\{0,1,\ldots,n-1\}$
, i.e. the integer lying in $\{0,1,\ldots,n-1\}$![]() such that $\langle \alpha \rangle _n\equiv \alpha \ ({\rm {mod}}\ n)$
such that $\langle \alpha \rangle _n\equiv \alpha \ ({\rm {mod}}\ n)$![]() .
.
Therefore,

In view of (2.1) and (2.2), we have

In view of [Reference Yeung22, proposition 4.1], we have

Then with the help of [Reference Yeung22, theorem 4.12] and lemma 2.2, we have
and
Hence,
Lemma 2.4 Let $p>3$![]() be a prime. For any $p$
be a prime. For any $p$![]() -adic integer $t$
-adic integer $t$![]() , we have
, we have

Proof. Set $m=(p-1)/2$![]() . It is easy to check that
. It is easy to check that

So lemma 2.4 is finished.
Now we evaluate $S_2$![]() modulo $p^2$
modulo $p^2$![]() . It is easy to obtain that
. It is easy to obtain that

with the help of lemmas 2.2, 2.4 and [Reference Yeung22, theorem 4.12].
Therefore, in view of (2.7), (2.8), (2.15) and (2.17), we immediately get the desired result

On the contrary, we use equation (2.5) to obtain

By using the package Sigma again, we find the following identity:

Thus,

Lemma 2.5 Let $p>5$![]() be a prime. If $0\leq j\leq (p-1)/2$
be a prime. If $0\leq j\leq (p-1)/2$![]() and $j\neq (p-1)/3$
and $j\neq (p-1)/3$![]() , then
, then
If $(p+1)/2\leq j\leq p-1$![]() , then
, then
Proof. If $0\leq j\leq (p-1)/2$![]() and $j\neq (p-1)/3$
and $j\neq (p-1)/3$![]() , then we have
, then we have

If $(p+1)/2\leq j\leq p-1$![]() , then
, then

Now the proof of lemma 2.5 is complete.
It is known that $\binom {2k}k\equiv 0\ ({\rm {mod}}\ p)$![]() for each $(p+1)/2\leq k\leq p-1$
for each $(p+1)/2\leq k\leq p-1$![]() , and it is easy to check that for each $0\leq j\leq (p-1)/2$
, and it is easy to check that for each $0\leq j\leq (p-1)/2$![]() :
:
These, with (2.18) yield

where

As above, with (2.10), (2.13), (2.14), lemma 2.2 and [Reference Yeung22, theorem 4.12], we have the following congruence modulo $p^2$![]() :
:

Now we evaluate $S_3$![]() . It is easy to see that
. It is easy to see that

In view of (2.17) and [Reference Yeung22, theorem 4.12], we immediately obtain
This, with (2.19) and (2.20) yields

Now the proof of theorem 1.1 is complete.
3. Proof of theorem 1.2
Proof of theorem 1.2 With the help of (2.4), we have

By loading the package Sigma in software Mathematica, we have the following identity:

Thus, replace $n$![]() by $p$
by $p$![]() in the above identity and then substitute it into (3.1), we have
in the above identity and then substitute it into (3.1), we have

Hence, we immediately obtain the following result by lemma 2.3:

where

It is easy to verify that

where

So,

It is easy to see that

On the other hand, we have

So by lemma 2.5 and the fact that for each $0\leq k\leq (p-1)/2$![]() ,
,

and for each $(p+1)/2\leq j\leq p-1$![]() ,
,
we have the following congruence modulo $p^3$![]() :
:

where

Hence, we have

where
By Sigma, we can find and prove the following identity:

In view of [Reference Sun17, lemma 3.1] and lemma 2.2, we have


It is easy to check that

And by [Reference Sury, Wang and Zhao21, (6)], we have


By Sigma, we find the following identity which can be proved by induction on $n$![]() :
:

So by setting $n=(p-1)/2$![]() in the above identity and with lemma 2.2, we have
in the above identity and with lemma 2.2, we have

And by (3.10), we have

It is easy to check that

By Sigma again, we have

So in view of lemma 2.2 and [Reference Yeung22], we have

Thus, by (3.10), we have

Also it is easy to see that

And by Sigma, we have

So in view of lemma 2.2, we have

Hence,

This, with (3.11) and (3.12) yields

By Sigma, we find the following identity which can be proved by induction on $n$![]() :
:

So in view of [Reference Yeung22], we have

This, with (3.9) and (3.13) yields

Thus, with (3.8) we have

So by (3.7), we have

Therefore, by (3.6) and (3.4), we deduce

Now, we evaluate the second sum on the right-hand side of (3.5). It is easy to see

By (3.14), we have

Now we consider the first sum of the right-hand side in (3.17):

The following identity is very important to us:

This, with [Reference Yeung22] yields

And by (3.19), we have

In view of (3.19) and [Reference Yeung22], we have

This, with (3.21) yields

Combining this with (3.20), we have

Thus, by (3.17) and (3.18), we have

This, with (3.5) and (3.16) yields

While

It is easy to check that

and

So by lemma 2.2 and the fact that $H_{p-1-k}^{(2)}\equiv -H_k^{(2)}\ ({\rm {mod}}\ p)$![]() for each $0\leq k\leq p-1$
for each $0\leq k\leq p-1$![]() , we have
, we have

and
So by $\binom {-\frac 12}{\frac {p-1}3}\equiv \binom {\frac {p-1}2}{\frac {p-1}3}\ ({\rm {mod}}\ p)$![]() and $\binom {p-1}{\frac {p-1}3}\equiv (-1)^{\frac {p-1}3}=1\ ({\rm {mod}}\ p)$
and $\binom {p-1}{\frac {p-1}3}\equiv (-1)^{\frac {p-1}3}=1\ ({\rm {mod}}\ p)$![]() , we can immediately obtain that
, we can immediately obtain that
This, with (3.22) yields

Now the proof of theorem 1.2 is complete.
Acknowledgements
The authors would like to thank the anonymous referee for careful reading of this manuscript and valuable comments, which make the paper more readable. This research was supported by the National Natural Science Foundation of China (Grant 12001288).