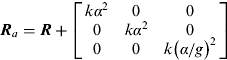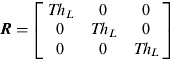1. INTRODUCTION
A Micro Electro Mechanical System (MEMS)-based Inertial Measurement Unit (IMU), which includes MEMS accelerometers and gyros, has a wide range of applications due to its low-cost, small size, and low power consumption. With given initial angles and gyros measurements, the Strap-down Inertial Navigation System (SINS) algorithm can provide orientation results (yaw, pitch and roll) through attitude updating. However, due to the large sensor noise and bias of low-cost MEMS sensors (Geiger et al., Reference Geiger, Bartholomeyczik, Breng, Gutmann, Hafen, Handrich, Huber, Jäckle, Kempfer, Kopmann, Kunz, Leinfelder, Ohmberger, Probst, Ruf, Spahlinger, Straub-Kalthoff, Stroda, Stumpf, Weber, Zimmermann and Zimmermann2008), such orientation results drift quickly over time and cannot satisfy long term performance requirements. On the other hand, accelerometer and magnetometer sensors can be integrated properly to become an electronic compass. It can sense the gravity and geomagnetic field, and eventually provides orientation results without long term drift effects. However such results would become inaccurate or even far from the truth, when the system is not totally stationary. In order to achieve a long term stable solution, it is a suitable system configuration for an Attitude and Heading Reference System (AHRS) to integrate two such systems together. An electronic compass can be used to estimate the gyros' drift and compensate the orientation errors of SINS, and then the SINS can maintain the performance for a long period of operations when the system is experiencing external accelerations.
A Kalman Filter (KF) is generally used for the integration in AHRS. Based on different attitude representations (Shuster, Reference Shuster1993), such as Euler angles and quaternion, different kinematic and measurement models are developed. With regard to the comparison between Euler angles and quaternion-based methods, Cooke et al. (Reference Cooke, Zyda, Pratt and McGhee1992) pointed out that, in the orientation task, the Euler method has more calculation efficiency than quaternion method, while the most significant advantage of the quaternion is that no singularity exists when the pitch angle pass through ±π/2 (Stuelpnagel, Reference Stuelpnagel1964).
Emura and Tachi (Reference Emura and Tachi1994) presented an Euler angle-based method, in which the KF state vectors were formed by three Euler angle components and three angular rates, and the Euler angle integration kinematics were adopted as the kinematic model of filter. The drawbacks of this method are that the Euler integration kinematic is a non-linear derivative equation and it suffers from a singularity problem.
Foxlin (Reference Foxlin1996) proposed an Euler angle error-based method and Setoodeh et al. (Reference Setoodeh, Khayatian and Farjah2004) proposed a similar method for integration. Indirect KF was adopted in their methods, and state vectors were formed by three Euler angle errors and three gyro biases. However, since the Euler angle errors in their methods were used to express the body frame (b frame) errors, the Euler angle integration kinematics were still adopted, so their methods also have non-linear and singularity problems.
In order to fix the singularity problem, for modern applications, Euler angles are often avoided in filter designs, and the quaternion has been the most widely used attitude parameterization. A major advantage of using quaternion is that the kinematics equation is linear in the quaternion and is also free of singularity (Markley et al., Reference Markley, Crassidis and Cheng2005). However, the observation model of the quaternion-based method is still non-linear (Nie et al., Reference Nie, Wu and Lin2010).
With regard to the non-linear problem, Markley et al. (Reference Markley, Crassidis and Cheng2005) presented a review of several filtering methods for non-linear attitude estimation. Although it is possible to find different families of approaches in literature, the Extended Kalman Filter (EKF) is still the standard technique for non-linear attitude estimation in practical terms. However, the EKF suffers from linearization error and it requires more system complexities and computational time than a regular KF. Although processing devices develop rapidly, it is still necessary to investigate the linear model for low-cost real-time systems. Qi and Moore (Reference Qi and Moore2002) presented a direct Kalman filtering approach, in which sensor non-linearities are pre-processed to adopt a simple and linear KF instead the EKF. In this way, the computational time is reduced but performance parameters are affected. Han and Wang (Reference Han and Wang2011a) proposed an integration method for IMU and magnetometers to avoid this non-linear problem, but the observation model in that paper suffers from the singularity problem when the pitch angle passes through ±π/2.
In addition, no approaches discussed above consider the impact of dynamic accelerations on the performance of an electronic compass. Actually, dynamic accelerations of the user platform would influence the gravity field measurement, and eventually affect orientation results of an electronic compass. An Adaptive Kalman Filter (AKF) can be adopted to fix such a problem. Wang et al. (Reference Wang, Yang, Hatch and Zhang2004) proposed an adaptive filter, in which the filter gain can be tuned according to the scalar dynamic accelerations sensed by accelerometers. However, in the gain adjustment procedure, it did not consider the influence of dynamic accelerations to the electronic compass heading, and then adds more errors into estimation results. Qin et al. (Reference Qin, Yuan, Chang, Xue and Yuan2009) adjusted the filter gain by tuning the process noise covariance matrix Q and R according to a fuzzy logic inference system; the drawback of this method is that the only tuning coefficient could not get the optimal Q and R at the same time. Munguia and Grau (Reference Munguia and Grau2011) proposed an adaptive EKF with an additive function noise in the measurement noise covariance matrix R, of which the increment decreases the influence of acceleration corrections when the user platform is not stationary. It works well during the low acceleration movement, but the drawback is that the additive function noise part could not decrease the influence of accelerometer corrections effectively when high acceleration occurred. Li and Wang (Reference Li and Wang2011) proposed an AKF for AHRS, with a multiplicative coefficient to tune R according to the system dynamics. However, it could not reflect the influence of accelerations on R accurately.
In this paper, a new AKF with linear models is proposed for low cost AHRS. The linear system kinematic model is developed based on the Psi-angle propagation equation (Goshen-Meskin and Bar-Itzhack, Reference Goshen-Meskin and Bar-Itzhack1992). The linear observation model is derived with the residuals of heading and accelerations in N and E directions of the local-level local-north frame. Considering the impact of dynamic accelerations, a dynamic scalar sensed by accelerometers is defined to determine the system movement mode. According to different movement modes, R can be tuned adaptively. Meanwhile, an additive function noise is introduced to tune R with the dynamic scalar in the low dynamic mode.
The contributions of this paper are as follows. Firstly, the long-standing non-linear problem in the AHRS is avoided to improve the computational efficiency. Secondly, the innovative adaptive procedure proposed here is effective. It can significantly improve the AHRS performance even under dynamic acceleration conditions.
This paper is organized as follows. In Section 2, a brief introduction to the orientation determination of electronic compasses is given to illustrate the impact of dynamic accelerations on orientation results. The system kinematic model and the corresponding system observation model are derived. The adaptive strategy for system dynamics is developed in Section 3. Experimental results with a low-cost AHRS device are presented in Section 4. For comparison, the same data in dynamic experiments is processed by the proposed method and two other adaptive methods from references. Finally, Section 5 draws concluding remarks and comments on future work.
2. ORIENTATION DETERMINATION BASED ON MAGNETOMETERS AND ACCELEROMETERS
The main task of AHRS is to determine orientation angles which are the main navigation parameters. These angles are also called Euler angles including yaw ψ, pitch θ and roll γ, which are defined as the rotation angles from the body frame (b frame) to the navigation frame (n frame). In this paper, the local-level local-North frame is chosen as the n frame. A good review of orientation methods of the SINS is given by Cooke et al., (Reference Cooke, Zyda, Pratt and McGhee1992), which will not be repeated here. In this section, a brief introduction is given for the magnetometer and accelerometer-based orientation determination.
An electronic compass can provide the heading and attitude angles with geomagnetic field and acceleration signals (Caruso, Reference Caruso2000). Since these measurements do not suffer from long term drift, they could be used for gyro measurements error estimation. When the system is stationary, the relationship between gravity field measurements of accelerometers in the b frame and the gravity vector in the n frame is formulated as:
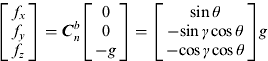 $$\left[ {\matrix{ {\,f_x} \cr {\,f_y} \cr {\,f_z} \cr}} \right] = {\bi C}_n^b \left[ {\matrix{ 0 \cr 0 \cr { - g} \cr}} \right] = \left[ {\matrix{ {{\rm sin}\,\theta} \cr { - {\rm sin}\,\gamma \, {\rm cos}\,\theta} \cr { - {\rm cos}\,\gamma \,{\rm cos}\,\theta} \cr}} \right]g$$
$$\left[ {\matrix{ {\,f_x} \cr {\,f_y} \cr {\,f_z} \cr}} \right] = {\bi C}_n^b \left[ {\matrix{ 0 \cr 0 \cr { - g} \cr}} \right] = \left[ {\matrix{ {{\rm sin}\,\theta} \cr { - {\rm sin}\,\gamma \, {\rm cos}\,\theta} \cr { - {\rm cos}\,\gamma \,{\rm cos}\,\theta} \cr}} \right]g$$where:
f x, f y and f z are measurements of accelerometers in the b frame.
C nb is the Direction Cosine Matrix (DCM) from the n frame to the b frame.
Based on Equation (1), attitude angles θ and γ can be calculated as:
The accuracy of these attitude angles is related to the accelerometers' bias, which is around 1 mrad/mg. In this paper, the bias of the employed accelerometers is 0·02 m/s2, so the accuracy of attitude angles is about 0·1 degree.
With measured attitude angles, the rotation relationship between the geomagnetic field vector measured by the magnetometers in the b frame Hb and the geomagnetic field vector in the n frame Hn could be expressed as:
where Hb and Hn are defined as:
With attitude angles measured by accelerometers, the DCM from the b frame to the n frame can be determined as:
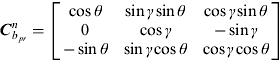 $${\bi C}_{b_{\,pr}}^n = \left[ {\matrix{ {\cos \theta} & {\sin \gamma \sin \theta} & {\cos \gamma \sin \theta} \cr 0 & {\cos \gamma} & { - \sin \gamma} \cr { - \sin \theta} & {\sin \gamma \cos \theta} & {\cos \gamma \cos \theta} \cr}} \right]$$
$${\bi C}_{b_{\,pr}}^n = \left[ {\matrix{ {\cos \theta} & {\sin \gamma \sin \theta} & {\cos \gamma \sin \theta} \cr 0 & {\cos \gamma} & { - \sin \gamma} \cr { - \sin \theta} & {\sin \gamma \cos \theta} & {\cos \gamma \cos \theta} \cr}} \right]$$After Hn is calculated from Equation (3), the magnetic heading can be determined:
Eventually, the orientation of the electronic compass can be determined by Equations (2) and (6). In practice, the electronic compass needs to be calibrated for soft iron and hard iron effects before orientation determination; Caruso (Reference Caruso1997) proposed a simple calibration method to determine the offset and scale factor values of an electronic compass.
Actually, an electronic compass can only work effectively under stationary or low acceleration conditions. From Equations (2), (3) and (6), we can see that if the system is not stationary, dynamic accelerations will influence the gravity field measurement in the b frame. So the attitude results will not be accurate and, eventually, these errors will be propagated into the magnetic heading result. If high dynamic accelerations occur, orientation results of the electronic compass will be significantly biased.
3. ADAPTIVE KALMAN FILTER SCHEME
Customary integration methods mentioned in the introduction section are subject to three annoyances: the non-linear problem, the singularity problem and the impact of dynamic accelerations. So the new design of AKF for IMU/magnetometers-based AHRS is based on the following considerations:
• First, the error state model is adopted, rather than the full state model. In the Euler angle-based full state model, because body angular rates are included in states of the KF, the body angular motion modelling is required. It is a difficult and complex task, leading to the non-linear and singularity problems. In the quaternion-based full state model, such problems in the kinematic model are avoided, but the corresponding observation model is still non-linear. Through adopting Euler angle errors expressing the n frame errors as the error state model, of which differential equation is linear, the non-linear and singularity problems in the kinematic model can be avoided.
• Second, acceleration residuals in both N and E directions in the n frame, rather than the pitch and roll errors, are used as the observation vector. Although it is a straightforward way to adopt orientation difference between gyros and an electronic compass as the observation vector in the KF, as Han and Wang (Reference Han and Wang2011a) did, it will lead to singularity problem in observation model when the pitch angle passes through ±π/2. The acceleration residuals in both N and E directions in the n frame contain equivalent frame errors information to the pitch and roll errors but without singularity problem, which will be analysed in the following subsection.
• Third, the impact of dynamic accelerations, which is illustrated in Section 2, should be taken into account. Common AHRS implementations have not considered such an impact which will actually decrease the filter performances under dynamic conditions. By tuning the gain of filter adaptively according to the magnitude of the dynamic acceleration, the filter can maintain the performance for a long period of operations when the system is undertaken external accelerations.
The system schematic diagram is shown in Figure 1.

Figure 1. Schematic diagram of IMU/magnetometers integrated AHRS.
3.1. System Kinematic Model
In this subsection, a linear kinematic model is developed based on the Psi-angle error model. It is well known that the Psi-angle error propagation equation of Inertial Navigation System (INS) is linear, in which the Psi-angle error Ψ represents the difference between the true navigation frame (n frame) and the platform frame. Here, the platform frame is a terminology in INS and could be viewed as the computed navigation frame (n c frame) in SINS (Blankinship, Reference Blankinship2008). As computational errors are negligible, arising from errors of gyros, the n c frame is different from the n frame. Thus, Ψ is used to represent such orientation difference between the n frame and the n c frame and equals to the rotation vector from the n frame to the n c frame. The differential equation of the Euler angle error expressing the n frame error for the AHRS could be expressed as:
where:
ωinn is the n frame rotation angular rate vector relative to the inertial frame (i frame) expressed in the n frame.
εn are errors of gyros expressed in the n frame, which include the constant bias Gb and the scale factor error Gs.
So the matrix form of the system kinematic model can be written as
where the error state vector is constructed as:
where:
the Ψ N, Ψ E and Ψ D are elements of Euler angle error Ψ.
G bx, G by and G bz are elements of the gyro bias G b expressed in the b frame.
G sx, G sy and G sz are elements of the scale factor error G s expressed in the b frame.
N, E and D are the subscripts of vector elements in the n frame.
x, y and z are the subscripts of vector elements in the b frame.
The system matrix F is defined as:
where:
 ${\bi \omega} _{in_c} ^{n_c} $ is the rotation rate of the n c frame respect to the i frame expressed in the n c frame.
${\bi \omega} _{in_c} ^{n_c} $ is the rotation rate of the n c frame respect to the i frame expressed in the n c frame. ${\bi \omega} _{in_c} ^{n_c}$ Ó is the skew symmetric matrix of
${\bi \omega} _{in_c} ^{n_c}$ Ó is the skew symmetric matrix of  ${\bi \omega} _{in_c} ^{n_c} $.
${\bi \omega} _{in_c} ^{n_c} $. ${\bi C}_b^{n_c} $ is the DCM from the b frame to the n c frame.
${\bi C}_b^{n_c} $ is the DCM from the b frame to the n c frame.G represents the angular increment of each epoch in the b frame measured by three axis gyros.
The process noise vector w is the independent Gaussian white noise with the zero mean:
where Q is the process noise covariance matrix.
3.2 System Observation Model
The acceleration residuals in the n frame, and the heading residuals between the electronic compass and gyros are used for the observation model. When the system is static, the sum of external accelerations in the b frame is equal to the gravity, and the acceleration vector in the n frame is:
The acceleration residuals in the n frame δf are defined as acceleration differences between the n frame and the n c frame:
in which fn is the acceleration vector in the n frame and ![]() ${\bi f}^{n_c} $ is the acceleration vector in the n c frame, which can be written as:
${\bi f}^{n_c} $ is the acceleration vector in the n c frame, which can be written as:
where fb is the acceleration vector in the b frame, which is the measurement vector of accelerometers.
Following the DCM chain rule (Savage, Reference Savage1998), ![]() ${\bi C}_b^{n_c} $ an be expressed as:
${\bi C}_b^{n_c} $ an be expressed as:
where ![]() ${\bi C}_n^{n_c} $ is the DCM from the n frame to the n c frame, and could be expressed as:
${\bi C}_n^{n_c} $ is the DCM from the n frame to the n c frame, and could be expressed as:
in which Ψ× is the skew symmetric matrix of the Psi-angle error vector Ψ.
Substituting Equations (12), (14), (15) and (16) into (13), the relationship between acceleration residuals in the n frame and the error states can be written as:
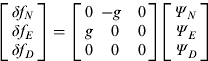 $$\left[ {\matrix{ {\delta f_N} \cr {\delta f_E} \cr {\delta f_D} \cr}} \right] = \left[ {\matrix{ 0 & {\hskip-5pt - g} & 0 \cr g & 0 & 0 \cr 0 & 0 & 0 \cr}} \right]\left[ {\matrix{ {\it \Psi _N} \cr {\it \Psi _E} \cr {\it \Psi _D} \cr}} \right]$
$$\left[ {\matrix{ {\delta f_N} \cr {\delta f_E} \cr {\delta f_D} \cr}} \right] = \left[ {\matrix{ 0 & {\hskip-5pt - g} & 0 \cr g & 0 & 0 \cr 0 & 0 & 0 \cr}} \right]\left[ {\matrix{ {\it \Psi _N} \cr {\it \Psi _E} \cr {\it \Psi _D} \cr}} \right]$where δf N, δf E and δf D are the elements of acceleration residuals in the n frame. From (17), the error state Ψ D is not observable.
The heading residual between the electronic compass and gyros can be written as (Foxlin, Reference Foxlin1996):
where:
 is the heading calculated by gyro measurements.
is the heading calculated by gyro measurements.ψ c is the heading from electronic compass.
Combining Equations (17) and (18), the observation model is obtained:
where Z = [δf NδfE δψ]T, and the observation matrix H is written as:
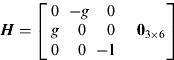 $${\bi H} = \left[ {\matrix{ 0 & {\hskip-4pt - g} & 0 \cr g & 0 & 0 \cr 0 & 0 & {\hskip-6pt - 1} \cr} \; \; \; \; {\bf 0}_{3 \times 6}} \right]$$
$${\bi H} = \left[ {\matrix{ 0 & {\hskip-4pt - g} & 0 \cr g & 0 & 0 \cr 0 & 0 & {\hskip-6pt - 1} \cr} \; \; \; \; {\bf 0}_{3 \times 6}} \right]$$and the measurement noise vector v is the independent Gaussian white noise with the zero mean:
where R is the measurement noise covariance matrix.
3.1. Adaptive Kalman Filter (AKF)
With regard to the AKF, there are primarily two different strategies (Wang et al., Reference Wang, Gopaul and Guo2010). The majority of adaptive algorithms focus on how to sequentially improve Q or R, or both of Q and R. Another strategy aims to find a balance between the time update and measurement update. In this paper, the proposed adaptive algorithm only deals with improving R, since dynamic accelerations mainly influence the measurement procedures.
3.3.1. Initialization of Q and R
In fact, the effect of the initial state vector along with its variance will be gradually reduced over time in KF operations. However, a major obstacle in applying a KF is specifying the covariance matrix Q and R (Louv, Reference Louv1984). Users should make their best effort to approximate Q and R with the available information about their applications. In general, specified values for the covariance matrix Q and R are experimental.
The process noise covariance matrix Q is composed as:
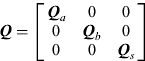 $${\bi Q} = \left[ {\matrix{ {{\bi Q}_a} & 0 & 0 \cr 0 & {{\bi Q}_b} & 0 \cr 0 & 0 & {{\bi Q}_s} \cr}} \right]$$
$${\bi Q} = \left[ {\matrix{ {{\bi Q}_a} & 0 & 0 \cr 0 & {{\bi Q}_b} & 0 \cr 0 & 0 & {{\bi Q}_s} \cr}} \right]$$where:
Qa is the matrix of the gyro angular random walk (ARW) process.
Qb is the matrix of the gyro bias driven by the rate random walk (RRW) process.
Qs is the matrix of gyro scale factor stability.
These parameters can be determined by Allan variance analysis (Lam et al., Reference Lam, Stamatakos, Woodruff and Ashtom2003; Han and Wang, Reference Han and Wang2011b) experiment.
When the AHRS system is static, the measurement noise covariance matrix R is composed as:
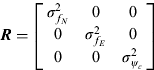 $${\bi R} = \left[ {\matrix{ {\sigma _{\,f_N} ^2} & 0 & 0 \cr 0 & {\sigma _{\,f_E} ^2} & 0 \cr 0 & 0 & {\sigma _{\psi _c} ^2} \cr}} \right]$$
$${\bi R} = \left[ {\matrix{ {\sigma _{\,f_N} ^2} & 0 & 0 \cr 0 & {\sigma _{\,f_E} ^2} & 0 \cr 0 & 0 & {\sigma _{\psi _c} ^2} \cr}} \right]$$where ![]() $\sigma _{\psi _c} ^2 $ is the variance of the electronic compass heading angle which can be determined by the electronic compass calibration experiment,
$\sigma _{\psi _c} ^2 $ is the variance of the electronic compass heading angle which can be determined by the electronic compass calibration experiment, ![]() $\sigma _{\,f_N} ^2 $ and
$\sigma _{\,f_N} ^2 $ and ![]() $\sigma _{\,f_E} ^2 $ are the variances of the acceleration residuals between the n c frame and the n frame as:
$\sigma _{\,f_E} ^2 $ are the variances of the acceleration residuals between the n c frame and the n frame as:
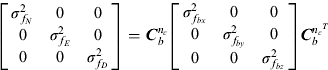 $$\left[ {\matrix{ {\sigma _{\,f_N} ^2} & 0 & 0 \cr 0 & {\sigma _{\,f_E} ^2} & 0 \cr 0 & 0 & {\sigma _{\,f_D} ^2} \cr}} \right] = {\bi C}_b^{n_c} \left[ {\matrix{ {\sigma _{\,f_{bx}} ^2} & 0 & 0 \cr 0 & {\sigma _{\,f_{by}} ^2} & 0 \cr 0 & 0 & {\sigma _{\,f_{bz}} ^2} \cr}} \right]{\bi C}_b^{{n_c}^{T}}$$
$$\left[ {\matrix{ {\sigma _{\,f_N} ^2} & 0 & 0 \cr 0 & {\sigma _{\,f_E} ^2} & 0 \cr 0 & 0 & {\sigma _{\,f_D} ^2} \cr}} \right] = {\bi C}_b^{n_c} \left[ {\matrix{ {\sigma _{\,f_{bx}} ^2} & 0 & 0 \cr 0 & {\sigma _{\,f_{by}} ^2} & 0 \cr 0 & 0 & {\sigma _{\,f_{bz}} ^2} \cr}} \right]{\bi C}_b^{{n_c}^{T}}$$where ![]() $\sigma _{\,f_{bx}} ^2$,
$\sigma _{\,f_{bx}} ^2$, ![]() $\sigma _{\,f_{by}} ^2 $ and
$\sigma _{\,f_{by}} ^2 $ and ![]() $\sigma _{\,f_{bz}} ^2 $ are the variances of accelerometer measurements in the b frame, which can be determined by an accelerometer calibration experiment.
$\sigma _{\,f_{bz}} ^2 $ are the variances of accelerometer measurements in the b frame, which can be determined by an accelerometer calibration experiment.
3.3.2. Adaptive Tuning of R
When the AHRS is stationary, the initialization of Q and R yield optimal gain for the best state estimation (Wang et al., Reference Wang, Yang, Hatch and Zhang2004). However, when the AHRS is in the dynamic mode, measurements of accelerometers consist of both gravity and dynamic accelerations, which lead to the change of R. In order to yield the optimal performance, R is tuned according to the dynamic scalar that is defined as:
where the g is gravity vector [0 0 g]T and the fb represents accelerometer measurements. The adaptable gain has the following scenarios:
• Non-acceleration mode: when
 $\alpha \leqslant \sqrt {\sigma _{\,f_{bx}} ^2 + \sigma _{\,f_{by}} ^2 + \sigma _{\,f_{by}} ^2 {\rm \;}} $, with R being defined in Equation (23), the filter is properly modelled as a stochastic process with an optimal estimate output.
$\alpha \leqslant \sqrt {\sigma _{\,f_{bx}} ^2 + \sigma _{\,f_{by}} ^2 + \sigma _{\,f_{by}} ^2 {\rm \;}} $, with R being defined in Equation (23), the filter is properly modelled as a stochastic process with an optimal estimate output.• Low-acceleration mode: when
 $\sqrt {\sigma _{\,f_{bx}} ^2 + \sigma _{\,f_{by}} ^2 + \sigma _{\,f_{by}} ^2 \;} \lt \alpha \leqslant Th_{acc}, $ such small dynamic acceleration could be treated as a part of measurement noise. The measurement noise covariance matrix should be adjusted on-line according to α:(26)where kα 2 is the additive function noise.
$\sqrt {\sigma _{\,f_{bx}} ^2 + \sigma _{\,f_{by}} ^2 + \sigma _{\,f_{by}} ^2 \;} \lt \alpha \leqslant Th_{acc}, $ such small dynamic acceleration could be treated as a part of measurement noise. The measurement noise covariance matrix should be adjusted on-line according to α:(26)where kα 2 is the additive function noise. $${\bi R}_a = {\bi R} + \left[ {\matrix{ {k\alpha ^2} & 0 & 0 \cr 0 & {k\alpha ^2} & 0 \cr 0 & 0 & {k\left( {\alpha /g} \right)^2} \cr}} \right]$
$${\bi R}_a = {\bi R} + \left[ {\matrix{ {k\alpha ^2} & 0 & 0 \cr 0 & {k\alpha ^2} & 0 \cr 0 & 0 & {k\left( {\alpha /g} \right)^2} \cr}} \right]$It is included to increase the accelerometer measurement noise proportionally to increments of the b frame acceleration. In order to include the influence of such acceleration on the magnetic heading calculation, the additive function noise for the magnetic heading measurement noise is formed as k(α/g)2, since the relationship between the accuracy of attitude angles calculated by accelerometers and accelerations is around 1 mrad/mg. Both the scale parameter k and the threshold Th acc can be determined by the experiments and the design requirements.
• High-acceleration mode: when α>Th acc, measurements of accelerometers are far from the value of the gravity, and then, the acceleration residuals and the heading calculated by accelerometers and the electronic compass are far away from the truth. In order to avoid such measurements affecting the filter, a proper solution is to set the gain of the KF to 0 during the high dynamic period, and then the system would become a stand-alone SINS. Therefore, R could be written as
(27) $${\bi R} = \left[ {\matrix{ {Th_L} & 0 & 0 \cr 0 & {Th_L} & 0 \cr 0 & 0 & {Th_L} \cr}} \right]$$
$${\bi R} = \left[ {\matrix{ {Th_L} & 0 & 0 \cr 0 & {Th_L} & 0 \cr 0 & 0 & {Th_L} \cr}} \right]$$
where Th L is a large number which would set the corresponding KF gain close to 0. Most real-world user platforms do not experience acceleration for a long period and error states of the KF are usually well estimated before such high acceleration occur. As a result, the stand-alone SINS can maintain the orientation calculation during the high acceleration interval. The threshold Th L is determined by experiments and the design requirements.
4. EXPERIMENTAL TEST
The experimental data were logged by an Xsens MTi sensor, which can output both raw sensor data and Euler angles at the same time. A magnetic calibration procedure was executed according to the user manual of MTi sensor before the experiment, and then the expected accuracy of electronic compass is 0·5 degree, the data refresh frequency was set to 100 Hz and other configurations of the MT software remained default. Experiments were implemented through both stationary and dynamic tests.
4.1. Stationary Test
In the stationary test, the system was fixed on a static table. Euler angle outputs of MTi and the proposed AKF were analysed. Euler angle errors in the stationary test are shown in Figure 2, and the error analysis is shown in Table 1. The results indicate that the accuracy of the AKF in the stationary test is within 0·1 degree.

Figure 2. Errors of Euler angles in the stationary test.
Table 1. RMS Error in the stationary test.

4.2. Low Dynamic Tests
The low dynamic tests were conducted with a BEI C-MIGITS II which is a tactical grade INS, and an Xsens MTi which is a low-cost AHRS. The MTi was firmly fastened to the top of the C-MIGITS II so that their dynamics would be the same during the test. The performance of the C-MIGITS II and the MTi is compared in Table 2.
Table 2. C-MIGITS II and MTi technical specifications.

As shown in Figure 3, the outputs of C-MIGITS II, MTi, the AKF_I proposed by Wang et al. (Reference Wang, Yang, Hatch and Zhang2004), the AKF_II proposed by Munguia and Grau (Reference Munguia and Grau2011), and the AKF_III proposed in this paper are very close to each other.

Figure 3. Time series outputs of different orientation results in the low dynamic test.
Setting the output of C-MIGITS II as the ground truth, Euler angle errors are plotted in Figure 4, and the error analysis is shown in Table 3. The results show that the accuracy of the proposed AKF_III in the low dynamic test is within 0·5 degree.

Figure 4. Errors of Euler angles in the low dynamic test.
Table 3. RMS Error in the low dynamic test.

4.3. High Dynamic Tests
Setting the output of C-MIGITS II as the ground truth, the Euler angle errors in the high dynamic test are plotted in Figure 5, and the error analysis is shown in Table 4. The results show that among all the tested filters, the proposed filter (AKF_III) can provide the best performance even during the high dynamic test.

Figure 5. Errors of Euler angles in the high dynamic test.
Table 4. RMS Error in the high dynamic test.

5. CONCLUDING REMARKS
This paper has presented an effective Adaptive Kalman Filter (AKF) for a Micro Electro Mechanical System (MEMS)-based Inertial Measurement Unit (IMU) and magnetometers integrated Attitude and Heading Reference System (AHRS).
A linear system error model based on the Psi-angle error model has been developed, and the corresponding observation model has been derived. Moreover, an effective adaptive strategy has been adopted in this method. According to the dynamic scalar which is defined to determine the system movement mode, the measurement noise covariance matrix R can be tuned adaptively to yield optimal performance during the dynamic periods. Experiments have shown that the proposed method can improve the orientation performance of low-cost sensors. With measurements from an Xsens MTi AHRS device, the proposed filter method can provide the stationary accuracy of less than 0·1 degree, and the low dynamic accuracy of better than 0·5 degree, the high dynamic accuracy of less than 1 degree, which are far better than the results from the commercial system itself or other existing filtering methods.
Further research is under way to consider the effects of magnetic anomalies, and integrate this system with other navigation systems, such as a vision-based system.
ACKNOWLEDGEMENTS
The first author would like to thank the China Scholarship Council (CSC) for supporting his studies at the University of New South Wales, Australia.