Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-24T09:30:33.583Z Has data issue: false hasContentIssue false
  • English
  • Français

Logic programming with function symbols: Checking termination of bottom-up evaluation through program adornments

Published online by Cambridge University Press:  25 September 2013

SERGIO GRECO ,
CRISTIAN MOLINARO  and
IRINA TRUBITSYNA
SERGIO GRECO
Affiliation:
DIMES, Università della Calabria E-mail: greco@dimes.unical.it, cmolinaro@dimes.unical.it, trubitsyna@dimes.unical.it)
CRISTIAN MOLINARO
Affiliation:
DIMES, Università della Calabria E-mail: greco@dimes.unical.it, cmolinaro@dimes.unical.it, trubitsyna@dimes.unical.it)
IRINA TRUBITSYNA
Affiliation:
DIMES, Università della Calabria E-mail: greco@dimes.unical.it, cmolinaro@dimes.unical.it, trubitsyna@dimes.unical.it)
Get access Rights & Permissions [Opens in a new window]

Abstract

Recent years have witnessed an increasing interest in enhancing answer set solvers by allowing function symbols. Since the introduction of function symbols makes common inference tasks undecidable, research has focused on identifying classes of programs allowing only a restricted use of function symbols while ensuring decidability of common inference tasks. Finitely-ground programs, introduced in Calimeri et al. (2008), are guaranteed to admit a finite number of stable models with each of them of finite size. Stable models of such programs can be computed and thus common inference tasks become decidable. Unfortunately, checking whether a program is finitely-ground is semi-decidable. This has led to several decidable criteria, called termination criteria, providing sufficient conditions for a program to be finitely-ground. This paper presents a new technique that, used in conjunction with current termination criteria, allows us to detect more programs as finitely-ground. Specifically, the proposed technique takes a logic program 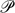${\cal P}$ and transforms it into an adorned program 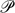${{\cal P}}$μ with the aim of applying termination criteria to 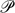${{\cal P}}$μ rather than 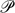${\cal P}$. The transformation is sound in that if the adorned program satisfies a certain termination criterion, then the original program is finitely-ground. Importantly, applying termination criteria to adorned programs rather than the original ones strictly enlarges the class of programs recognized as finitely-ground.

Keywords

logic programming with function symbolsbottom-up evaluationprogram evaluation terminationstable models
Type
Regular Papers
Information
Theory and Practice of Logic Programming , Volume 13 , Issue 4-5: 29th International Conference on Logic Programming , July 2013 , pp. 737 - 752
Copyright
Copyright © 2013 [SERGIO GRECO, CRISTIAN MOLINARO and IRINA TRUBITSYNA] 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alviano, M., Faber, W. and Leone, N. 2010. Disjunctive asp with functions: Decidable queries and effective computation. Theory and Practice of Logic Programming 10, 4–6, 497–512.CrossRefGoogle Scholar
Arts, T. and Giesl, J. 2000. Termination of term rewriting using dependency pairs. Theoretical Computer Science 236, 1–2, 133–178.CrossRefGoogle Scholar
Baselice, S., Bonatti, P. A. and Criscuolo, G. 2009. On finitely recursive programs. Theory and Practice of Logic Programming 9, 2, 213–238.Google Scholar
Bonatti, P. A. 2004. Reasoning with infinite stable models. Artificial Intelligence 156, 1, 75–111.Google Scholar
Bruynooghe, M., Codish, M., Gallagher, J. P., Genaim, S. and Vanhoof, W. 2007. Termination analysis of logic programs through combination of type-based norms. ACM Transactions on Programming Languages and Systems 29, 2.CrossRefGoogle Scholar
Calautti, M., Greco, S. and Trubitsyna, I. 2013. Detecting decidable classes of finitely ground logic programs with function symbols. In International Symposium on Principles and Practice of Declarative Programming (to appear).CrossRefGoogle Scholar
Calimeri, F., Cozza, S., Ianni, G. and Leone, N. 2008. Computable functions in asp: Theory and implementation. In International Conference on Logic Programming, 407–424.Google Scholar
Calimeri, F., Cozza, S., Ianni, G. and Leone, N. 2010. Enhancing asp by functions: Decidable classes and implementation techniques. In AAAI Conference on Artificial Intelligence.Google Scholar
Codish, M., Lagoon, V. and Stuckey, P. J. 2005. Testing for termination with monotonicity constraints. In International Conference on Logic Programming, 326–340.Google Scholar
De Schreye, D. and Decorte, S. 1994. Termination of logic programs: The never-ending story. Journal of Logic Programming 19/20, 199–260.CrossRefGoogle Scholar
Deutsch, A., Nash, A. and Remmel, J. B. 2008. The chase revisited. In Symposium on Principles of Database Systems, 149–158.Google Scholar
Endrullis, J., Waldmann, J. and Zantema, H. 2008. Matrix interpretations for proving termination of term rewriting. Journal of Automated Reasoning 40, 2–3, 195–220.Google Scholar
Fagin, R., Kolaitis, P. G., Miller, R. J. and Popa, L. 2005. Data ex- change: Semantics and query answering. TCS 336, 1, 89–124.Google Scholar
Ferreira, M. C. F. and Zantema, H. 1996. Total termination of term rewriting. Applicable Algebra in Engineering, Communication and Computing 7, 2, 133–162.CrossRefGoogle Scholar
Gebser, M., Schaub, T. and Thiele, S. 2007. Gringo: A new grounder for answer set programming. In International Conference on Logic Programming and Nonmonotonic Reasoning, 266–271.Google Scholar
Gelfond, M. and Lifschitz, V. 1988. The stable model semantics for logic programming. In International Joint Conference and Symposium on Logic Programming, 1070–1080.Google Scholar
Gelfond, M. and Lifschitz, V. 1991. Classical negation in logic programs and disjunctive databases. New Generation Computing 9, 3/4, 365–386.Google Scholar
Grau, B. C., Horrocks, I., Krötzsch, M., Kupke, C., Magka, D., Motik, B. and Wang, Z. 2012. Acyclicity conditions and their application to query answering in description logics. In KR.Google Scholar
Greco, S., Molinaro, C. and Spezzano, F. 2012a. Incomplete Data and Data Dependencies in Relational Databases, Synthesis Lectures on Data Management, Morgan & Claypool Publishers.Google Scholar
Greco, S., Molinaro, C. and Trubitsyna, I. 2013. Bounded programs: A new decidable class of logic programs with function symbols. In International Joint Conference on Artificial Intelligence (to appear).Google Scholar
Greco, S. and Spezzano, F. 2010. Chase termination: A constraints rewriting approach. Proceeding of the Very Large Data Base Conference 3, 1, 93–104.Google Scholar
Greco, S., Spezzano, F. and Trubitsyna, I. 2011. Stratification criteria and rewriting techniques for checking chase termination. Proceeding of the Very Large Data Base Conference 4, 11, 1158–1168.Google Scholar
Greco, S., Spezzano, F. and Trubitsyna, I. 2012b. On the termination of logic programs with function symbols. In International Conference on Logic Programming (Technical Communications), 323–333.Google Scholar
Krötzsch, M. and Rudolph, S. 2011. Extending decidable existential rules by joining acyclicity and guardedness. In IJCAI, 963–968.Google Scholar
Lierler, Y. and Lifschitz, V. 2009. One more decidable class of finitely ground programs. In International Conference on Logic Programming, 489–493.Google Scholar
Marchiori, M. 1996. Proving existential termination of normal logic programs. In Algebraic Methodology and Software Technology, 375–390.Google Scholar
Marnette, B. 2009. Generalized schema-mappings: from termination to tractability. In Symposium on Principles of Database Systems, 13–22.Google Scholar
Meier, M., Schmidt, M. and Lausen, G. 2009. On chase termination beyond stratification. Proceeding of the Very Large Data Base Conference 2, 1, 970–981.Google Scholar
Nguyen, M. T., Giesl, J., Schneider-Kamp, P. and De Schreye, D. 2007. Termination analysis of logic programs based on dependency graphs. In International Symposium on Logic-based Program Synthesis and Transformation, 8–22.Google Scholar
Nishida, N. and Vidal, G. 2010. Termination of narrowing via termination of rewriting. Applicable Algebra in Engineering, Communication and Computing 21, 3, 177–225.CrossRefGoogle Scholar
Ohlebusch, E. 2001. Termination of logic programs: Transformational methods revisited. Applicable Algebra in Engineering, Communication and Computing 12, 1/2, 73–116.Google Scholar
Schneider-Kamp, P., Giesl, J. and Nguyen, M. T. 2009a. The dependency triple framework for termination of logic programs. In International Symposium on Logic-based Program Synthesis and Transformation, 37–51.Google Scholar
Schneider-Kamp, P., Giesl, J., Serebrenik, A. and Thiemann, R. 2009b. Automated termination proofs for logic programs by term rewriting. ACM Transactions on Computational Logic 11, 1.Google Scholar
Schneider-Kamp, P., Giesl, J., Ströder, T., Serebrenik, A. and Thiemann, R. 2010. Automated termination analysis for logic programs with cut. Theory and Practice of Logic Programming 10, 4–6, 365–381.CrossRefGoogle Scholar
Serebrenik, A. and De Schreye, D. 2005. On termination of meta-programs. Theory and Practice of Logic Programming 5, 3, 355–390.Google Scholar
Sternagel, C. and Middeldorp, A. 2008. Root-labeling. In Rewriting Techniques and Applications, 336–350.Google Scholar
Syrjänen, T. 2001. Omega-restricted logic programs. In International Conference on Logic Programming and Nonmonotonic Reasoning, 267–279.Google Scholar
Voets, D. and De Schreye, D. 2011. Non-termination analysis of logic programs with integer arithmetics. Theory and Practice of Logic Programming 11, 4–5, 521–536.Google Scholar
Zantema, H. 1994. Termination of term rewriting: Interpretation and type elimination. Journal of Symbolic Computation 17, 1, 23–50.Google Scholar
Zantema, H. 1995. Termination of term rewriting by semantic labelling. Fundamenta Informaticae 24, 1/2, 89–105.CrossRefGoogle Scholar