Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-25T10:20:43.625Z Has data issue: false hasContentIssue false
  • English
  • Français

Beyond NP: Quantifying over Answer Sets

Published online by Cambridge University Press:  20 September 2019

GIOVANNI AMENDOLA Open the ORCID record for GIOVANNI AMENDOLA [Opens in a new window] ,
FRANCESCO RICCA Open the ORCID record for FRANCESCO RICCA [Opens in a new window]  and
MIROSLAW TRUSZCZYNSKI
GIOVANNI AMENDOLA
Affiliation:
University of Calabria, Rende, Italy (e-mails: amendola@mat.unical.it, ricca@mat.unical.it)
FRANCESCO RICCA
Affiliation:
University of Calabria, Rende, Italy (e-mails: amendola@mat.unical.it, ricca@mat.unical.it)
MIROSLAW TRUSZCZYNSKI
Affiliation:
University of Kentucky, KY, USA (e-mail: mirek@cs.uky.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

Answer Set Programming (ASP) is a logic programming paradigm featuring a purely declarative language with comparatively high modeling capabilities. Indeed, ASP can model problems in NP in a compact and elegant way. However, modeling problems beyond NP with ASP is known to be complicated, on the one hand, and limited to problems in 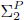$\[\Sigma _2^P\]$ on the other. Inspired by the way Quantified Boolean Formulas extend SAT formulas to model problems beyond NP, we propose an extension of ASP that introduces quantifiers over stable models of programs. We name the new language ASP with Quantifiers (ASP(Q)). In the paper we identify computational properties of ASP(Q); we highlight its modeling capabilities by reporting natural encodings of several complex problems with applications in artificial intelligence and number theory; and we compare ASP(Q) with related languages. Arguably, ASP(Q) allows one to model problems in the Polynomial Hierarchy in a direct way, providing an elegant expansion of ASP beyond the class NP.

Keywords

ASPQuantified LogicsPolynomial Hierarchy
Type
Original Article
Information
Theory and Practice of Logic Programming , Volume 19 , Special Issue 5-6: 35th International Conference on Logic Programming , September 2019 , pp. 705 - 721
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alviano, M., Amendola, G., Dodaro, C., Leone, N., Maratea, M., and Ricca, F. 2019. Evaluation of disjunctive programs in WASP. In LPNMR. Lecture Notes in Computer Science, vol. 11481. Springer, 241–255.Google Scholar
Alviano, M., Dodaro, C., Leone, N., and Ricca, F. 2015. Advances in WASP. In LPNMR. LNCS, vol. 9345. Springer, 40–54.Google Scholar
Amendola, G. 2018. Towards quantified answer set programming. In RCRA@FLoC. CEUR Workshop Proceedings, vol. 2271. CEUR-WS.org.Google Scholar
Ben-Eliyahu, R. and Dechter, R. 1996. On computing minimal models. Ann. Math. Artif. Intell. 18, 1, 3–27.10.1007/BF02136172CrossRefGoogle Scholar
Biere, A., Heule, M., van Maaren, H., and Walsh, T., Eds. 2009. Handbook of Satisfiability. Frontiers in Artificial Intelligence and Applications, vol. 185. IOS Press.Google Scholar
Blumer, A., Ehrenfeucht, A., Haussler, D., and Warmuth, M. K. 1989. Learnability and the Vapnik-Chervonenkis dimension. J. ACM 36, 4, 929–965.10.1145/76359.76371CrossRefGoogle Scholar
Bogaerts, B., Janhunen, T., and Tasharrofi, S. 2016. Stable-unstable semantics: Beyond NP with normal logic programs. TPLP 16, 5-6, 570–586.Google Scholar
Bordeaux, L. and Monfroy, E. 2002. Beyond NP: arc-consistency for quantified constraints. In CP. LNCS, vol. 2470. Springer, 371–386.Google Scholar
Brewka, G., Eiter, T., and Truszczynski, M. 2011. Answer set programming at a glance. Commun. ACM 54, 12, 92–103.10.1145/2043174.2043195CrossRefGoogle Scholar
Buccafurri, F., Leone, N., and Rullo, P. 2000. Enhancing disjunctive datalog by constraints. IEEE Trans. Knowl. Data Eng. 12, 5, 845–860.10.1109/69.877512CrossRefGoogle Scholar
Cadoli, M., Eiter, T., and Gottlob, G. 1997. Default logic as a query language. IEEE Trans. Knowl. Data Eng. 9, 3, 448–463.10.1109/69.599933CrossRefGoogle Scholar
Cao, F., Du, D.-Z., Gao, B., Wan, P.-J., and Pardalos, P. M. 1995. Minimax Problems in Combinatorial Optimization. Springer US, Boston, MA, 269–292.Google Scholar
Chung, F. R. 1989. Pebbling in hypercubes. SIAM J. Discret. Math. 2, 4 (Nov.), 467–472.10.1137/0402041CrossRefGoogle Scholar
Dantsin, E., Eiter, T., Gottlob, G., and Voronkov, A. 2001. Complexity and expressive power of logic programming. ACM Comput. Surv. 33, 3, 374–425.10.1145/502807.502810CrossRefGoogle Scholar
Denecker, M., Lierler, Y., Truszczynski, M., and Vennekens, J. 2012. A Tarskian informal semantics for answer set programming. In ICLP-TC. LIPIcs, vol. 17. 277–289.Google Scholar
Denecker, M. and Vennekens, J. 2014. The well-founded semantics is the principle of inductive definition, revisited. In KR. AAAI Press.Google Scholar
Dodaro, C., Gasteiger, P., Leone, N., Musitsch, B., Ricca, F., and Schekotihin, K. 2016. Combining answer set programming and domain heuristics for solving hard industrial problems (application paper). TPLP 16, 5-6, 653–669.Google Scholar
Eiter, T., Faber, W., Leone, N., and Pfeifer, G. 2000. Declarative problem-solving using the dlv system. In Logic-based Artificial Intelligence. 79–103.Google Scholar
Eiter, T. and Gottlob, G. 1995. On the computational cost of disjunctive logic programming: Propositional case. Ann. Math. Artif. Intell. 15, 3-4, 289–323.10.1007/BF01536399CrossRefGoogle Scholar
Eiter, T., Ianni, G., Lukasiewicz, T., Schindlauer, R., and Tompits, H. 2008. Combining answer set programming with description logics for the semantic web. Artif. Intell. 172, 12-13, 1495–1539.Google Scholar
Eiter, T. and Polleres, A. 2006. Towards automated integration of guess and check programs in answer set programming: a meta-interpreter and applications. TPLP 6, 1-2, 23–60.Google Scholar
Erdem, E., Gelfond, M., and Leone, N. 2016. Applications of answer set programming. AI Magazine 37, 3, 53–68.10.1609/aimag.v37i3.2678CrossRefGoogle Scholar
Faber, W. and Woltran, S. 2009. A framework for programming with module consequences. In SEA. CEUR Workshop Proceedings, vol. 546. CEUR-WS.org, 34–48.Google Scholar
Faber, W. and Woltran, S. 2011. Manifold answer-set programs and their applications. In Logic Programming, Knowledge Representation, and Nonmonotonic Reasoning. LNCS, vol. 6565. 44–63.Google Scholar
Gebser, M., Kaminski, R., Kaufmann, B., Romero, J., and Schaub, T. 2015. Progress in clasp series 3. In LPNMR. LNCS, vol. 9345. Springer, 368–383.Google Scholar
Gebser, M., Kaminski, R., and Schaub, T. 2011. Complex optimization in answer set programming. TPLP 11, 4-5, 821–839.Google Scholar
Gebser, M., Leone, N., Maratea, M., Perri, S., Ricca, F., and Schaub, T. 2018. Evaluation techniques and systems for answer set programming: a survey. In IJCAI. ijcai.org, 5450–5456.Google Scholar
Gebser, M., Maratea, M., and Ricca, F. 2017. The sixth answer set programming competition. J. Artif. Intell. Res. 60, 41–95.Google Scholar
Gebser, M., Obermeier, P., Schaub, T., Ratsch-Heitmann, M., and Runge, M. 2018. Routing driverless transport vehicles in car assembly with answer set programming. TPLP 18, 3-4, 520–534.Google Scholar
Gebser, M. and Schaub, T. 2016. Modeling and language extensions. AI Magazine 37, 3, 33–44.10.1609/aimag.v37i3.2673CrossRefGoogle Scholar
Gelfond, M. and Lifschitz, V. 1991. Classical negation in logic programs and disjunctive databases. New Generation Comput. 9, 3/4, 365–386.10.1007/BF03037169CrossRefGoogle Scholar
Hurlbert, G. 1999. A Survey of Graph Pebbling. Congr. Num. 139, math.CO/0406024, 41–64.Google Scholar
Ko, , Ker-Iand Lin, C.-L. 1995. On the Complexity of Min-Max Optimization Problems and their Approximation. Springer US, Boston, MA, 219–239.Google Scholar
Leone, N., Pfeifer, G., Faber, W., Eiter, T., Gottlob, G., Perri, S., and Scarcello, F. 2006. The DLV system for knowledge representation and reasoning. ACM Trans. Comput. Log. 7, 3, 499–562.10.1145/1149114.1149117CrossRefGoogle Scholar
Lifschitz, V. 2002. Answer set programming and plan generation. Artif. Intell. 138, 1-2, 39–54.Google Scholar
Milans, K. and Clark, B. 2006. The complexity of graph pebbling. SIAM J. Discret. Math. 20, 3 (Mar.), 769–798.10.1137/050636218CrossRefGoogle Scholar
Oikarinen, E. and Janhunen, T. 2006. Modular equivalence for normal logic programs. In ECAI. Frontiers in Artificial Intelligence and Applications, vol. 141. IOS Press, 412–416.Google Scholar
Redl, C. 2017. Explaining inconsistency in answer set programs and extensions. In LPNMR. LNCS, vol. 10377. Springer, 176–190.Google Scholar
Romero, J., Schaub, T., and Son, T. C. 2017. Generalized answer set planning with incomplete information. CEUR Workshop Proceedings 1868.Google Scholar
Rossi, F., van Beek, P., and Walsh, T. 2006. Introduction. In Handbook of Constraint Programming. Foundations of Artificial Intelligence, vol. 2. Elsevier, 3–12.10.1016/S1574-6526(06)80005-2CrossRefGoogle Scholar
Schaefer, M. 1999. Deciding the Vapnik-Chervonenkis dimension in $\[\Sigma _3^p\]$-complete. J. Comput. Syst. Sci. 58, 1, 177–182.Google Scholar
Stockmeyer, L. J. 1976. The polynomial-time hierarchy. Theor. Comput. Sci. 3, 1, 1–22.Google Scholar
Stockmeyer, L. J. and Meyer, A. R. 1973. Word problems requiring exponential time: Preliminary report. In STOC. ACM, 1–9.Google Scholar
Vapnik, V. 1998. Statistical learning theory. Wiley.Google Scholar
Vapnik, V. N. and Chervonenkis, A. Y. 2015. On the Uniform Convergence of Relative Frequencies of Events to Their Probabilities. Springer International Publishing, Cham, 11–30.Google Scholar
Supplementary material: PDF

Amendola et al. supplementary material

Online Appendix

Download Amendola et al. supplementary material(PDF)
PDF 105.3 KB