Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T11:28:03.584Z Has data issue: false hasContentIssue false
  • English
  • Français

Vectorial parameterizations of pose

Published online by Cambridge University Press:  10 December 2021

Timothy D. Barfoot Open the ORCID record for Timothy D. Barfoot [Opens in a new window] ,
James R. Forbes  and
Gabriele M. T. D’Eleuterio
Timothy D. Barfoot*
Affiliation:
University of Toronto Institute for Aerospace Studies, Toronto, Canada
James R. Forbes
Affiliation:
Department of Mechanical Engineering, McGill University, Montreal, Canada
Gabriele M. T. D’Eleuterio
Affiliation:
University of Toronto Institute for Aerospace Studies, Toronto, Canada
*
*Corresponding author. E-mail: tim.barfoot@utoronto.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

Robotics and computer vision problems commonly require handling rigid-body motions comprising translation and rotation – together referred to as pose. In some situations, a vectorial parameterization of pose can be useful, where elements of a vector space are surjectively mapped to a matrix Lie group. For example, these vectorial representations can be employed for optimization as well as uncertainty representation on groups. The most common mapping is the matrix exponential, which maps elements of a Lie algebra onto the associated Lie group. However, this choice is not unique. It has been previously shown how to characterize all such vectorial parameterizations for SO(3), the group of rotations. Some results are also known for the group of poses, where it is possible to build a family of vectorial mappings that includes the matrix exponential as well as the Cayley transformation. We extend what is known for these pose mappings to the 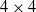$4 \times 4$ representation common in robotics and also demonstrate three different examples of the proposed pose mappings: (i) pose interpolation, (ii) pose servoing control, and (iii) pose estimation in a pointcloud alignment problem. In the pointcloud alignment problem, our results lead to a new algorithm based on the Cayley transformation, which we call CayPer.

Keywords

matrix Lie groupsstate estimationvector representation of rotationpose
Type
Research Article
Information
Robotica , Volume 40 , Issue 7 , July 2022 , pp. 2409 - 2427
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Mozzi, G., Discorso matematico sopra il rotamento momentaneo dei corpi (Donate Campo, 1763).Google Scholar
Chasles, M., “Note sur les propriétés générales du système de deux corps semblables entr’eux et placés d’une manière quelconque dans l’espace; et sur le déplacement fini ou infiniment petit d’un corps solide libre,” Bulletin des Sciences Mathématiques, Férussac 14, 321–26 (1830).Google Scholar
Ball, R. S., A Treatise on the Theory of Screws (Cambridge University Press, London, 1900).Google Scholar
Murray, R. M., Li, Z. and Sastry, S., A Mathematical Introduction to Robotic Manipulation (CRC Press, London, 1994).Google Scholar
Barfoot, T. D., State Estimation for Robotics (Cambridge University Press, Cambridge, 2017).CrossRefGoogle Scholar
Barfoot, T. D. and Furgale, P. T., “Associating uncertainty with three-dimensional poses for use in estimation problems,” IEEE Trans. Rob. 30(3), 679–693 (2014), (code).CrossRefGoogle Scholar
Chirikjian, G. S., Stochastic Models, Information Theory, and Lie Groups: Classical Results and Geometric Methods, vol. 1–2 (Birkhauser, New York, 2009).CrossRefGoogle Scholar
Hughes, P. C., Spacecraft Attitude Dynamics (John Wiley and Sons, New York, 1986).Google Scholar
Bauchau, O. A. and Trainelli, L., “The vectorial parameterization of rotation,” Nonlinear Dyn. 32(1), 71–92 (2003).CrossRefGoogle Scholar
Bauchau, O. A. and Choi, J.-Y., “The vector parameterization of motion,” Nonlinear Dyn. 33(2), 165–188 (2003).CrossRefGoogle Scholar
Bauchau, O. A. and Li, L., “Tensorial parameterization of rotation and motion,” J. Comput. Nonlinear Dyn. 6(3), 031007-1–031007-8 (2011).Google Scholar
Bauchau, O. A., Flexible Multibody Dynamics (Springer Science & Business Media, London, 2011).Google Scholar
Borri, M., Trainelli, L. and Bottasso, C. L., “On representations and parameterizations of motion,” Multibody Syst. Dyn. 4(2), 129–193 (2000).CrossRefGoogle Scholar
Selig, J. M., “Cayley Maps for SE(3),” 12th International Federation for the Promotion of Mechanism and Machine Science World Congress (London South Bank University, 2007) p. 6.Google Scholar
Cayley, A., “Sur quelques propriétés des déterminants gauches,” J. für die reine und angewandte Mathematik 1846(32), 119–123 (1846).Google Scholar
D’Eleuterio, G. M. T. and Barfoot, T. D., “On the Eigenstructure of Rotations and Poses: Commonalities and Peculiarities” (2021), in preparation for submission.Google Scholar
Stuelpnagel, J., “On the parametrization of the three-dimensional rotation group,” SIAM Rev. 6(4), 422–430 (1964).CrossRefGoogle Scholar
Condurache, D. and Ciureanu, I.-A., “Baker–Campbell–Hausdorff–Dynkin formula for the lie algebra of rigid body displacements,” Mathematics 8(7), 1185 (2020).CrossRefGoogle Scholar
Han, S. and Bauchau, O. A., “Manipulation of motion via dual entities,” Nonlinear Dyn. 85(1), 509–524 (2016).CrossRefGoogle Scholar
Han, S. and Bauchau, O. A., “On the global interpolation of motion,” Comput. Methods Appl. Mech. Eng. 337, 352–386 (2018).CrossRefGoogle Scholar
Barfoot, T. D., Forbes, J. R. and Furgale, P. T., “Pose estimation using linearized rotations and quaternion algebra,” Acta Astronautica 68(1–2), 101–112 (2011).CrossRefGoogle Scholar
Junkins, J. L., Majji, M., Macomber, B., Davis, J., Doebbler, J. and Nosterk, R., “Small body proximity sensing with a Novel HD 3D ladar system,” Adv. Astronaut. Sci. 141, 341–354 (2011).Google Scholar
Majji, M., Davis, J., Doebbler, J., Junkins, J., Macomber, B., Vavrina, M. and Vian, J., “Terrain Mapping and Landing Operations Using Vision Based Navigation Systems,” AIAA Guidance, Navigation, and Control Conference (2011) p. 6581.Google Scholar
Mortari, D., Markley, F. L. and Singla, P., “Optimal linear attitude estimator,” J. Guidance Control Dyn. 30(6), 1619–1627 (2007).CrossRefGoogle Scholar
Qian, D., Charland-Arcand, G. and Forbes, J. R., “TWOLATE: Total Registration of Point-Clouds Using a Weighted Optimal Linear Attitude and Translation Estimator,” 2020 IEEE Conference on Control Technology and Applications (CCTA) (IEEE, 2020) pp. 43–48.CrossRefGoogle Scholar
Wong, X. I. and Majji, M. “A structured light system for relative navigation applications,” IEEE Sens. J. 16(17), 6662–6679 (2016).CrossRefGoogle Scholar
Wong, X. I., Singla, P., Lee, T. and Majji, M., “Optimal Linear Attitude Estimator for Alignment of Point Clouds,” 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW) (IEEE, 2018) pp. 1577–15778.CrossRefGoogle Scholar
Maimone, M., Cheng, Y. and Matthies, L., “Two years of visual odometry on the mars exploration rovers,” J. Field Rob. 24(3), 169–186 (2007).CrossRefGoogle Scholar
Matthies, L. and Shafer, S., “Error modeling in stereo navigation,” IEEE J. Rob. Autom. 3(3), 239–248 (1987).CrossRefGoogle Scholar
Yang, H., Shi, J. and Carlone, L., “Teaser: Fast and certifiable point cloud registration,” IEEE Trans. Rob. 37(2), 314–333 (2020).CrossRefGoogle Scholar