Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-12T19:54:34.209Z Has data issue: false hasContentIssue false
  • English
  • Français

TRIAL AND ERROR MATHEMATICS I: DIALECTICAL AND QUASIDIALECTICAL SYSTEMS

Published online by Cambridge University Press:  01 February 2016

JACOPO AMIDEI ,
DUCCIO PIANIGIANI ,
LUCA SAN MAURO ,
GIULIA SIMI  and
ANDREA SORBI
JACOPO AMIDEI*
Affiliation:
Scuola Normale Superiore
DUCCIO PIANIGIANI*
Affiliation:
Università Degli Studi di Siena
LUCA SAN MAURO*
Affiliation:
Scuola Normale Superiore
GIULIA SIMI*
Affiliation:
Università Degli Studi di Siena
ANDREA SORBI*
Affiliation:
Scuola Normale Superiore
*
*SCUOLA NORMALE SUPERIORE I-56126 PISA, ITALY E-mail: jacopo.amidei@sns.it
†DIPARTIMENTO DI INGEGNERIA INFORMATICA E SCIENZE MATEMATICHE UNIVERSITÀ DEGLI STUDI DI SIENA I-53100 SIENA, ITALY E-mail: duccio.pianigiani@unisi.it
‡SCUOLA NORMALE SUPERIORE I-56126 PISA, ITALY E-mail: luca.sanmauro@sns.it
§DIPARTIMENTO DI INGEGNERIA INFORMATICA E SCIENZE MATEMATICHE UNIVERSITÀ DEGLI STUDI DI SIENA I-53100 SIENA, ITALY E-mail: giulia.simi@unisi.it
DIPARTIMENTO DI INGEGNERIA INFORMATICA E SCIENZE MATEMATICHE UNIVERSITÀ DEGLI STUDI DI SIENA I-53100 SIENA, ITALY E-mail: andrea.sorbi@unisi.it
Get access Rights & Permissions [Opens in a new window]

Abstract

We define and study quasidialectical systems, which are an extension of Magari’s dialectical systems, designed to make Magari’s formalization of trial and error mathematics more adherent to the real mathematical practice of revision: our proposed extension follows, and in several regards makes more precise, varieties of empiricist positions à la Lakatos. We prove several properties of quasidialectical systems and of the sets that they represent, called quasidialectical sets. In particular, we prove that the quasidialectical sets are 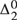${\rm{\Delta }}_2^0$ sets in the arithmetical hierarchy. We distinguish between “loopless” quasidialectal systems, and quasidialectical systems “with loops”. The latter ones represent exactly those coinfinite c.e. sets, that are not simple. In a subsequent paper we will show that whereas the dialectical sets are ω-c.e., the quasidialectical sets spread out throughout all classes of the Ershov hierarchy of the ${\rm{\Delta }}_2^0$ sets.

Keywords

03A9903D5503D99
Type
Research Article
Information
The Review of Symbolic Logic , Volume 9 , Issue 2 , June 2016 , pp. 299 - 324
Copyright
Copyright © Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Amidei, J., Pianigiani, D., San Mauro, L., & Sorbi, A. Trial and error mathematics II: Dialectical sets and quasidialectical sets, their degrees, and their distribution within the class of limit sets. Preprint, 2014, submitted.Google Scholar
Angluin, D., & Smith, C. H. (1983). Inductive inference: Theory and methods. ACM Computing Surveys (CSUR), 15(3), 237–269.CrossRefGoogle Scholar
Bernardi, C. (1974). Aspetti ricorsivi degli insiemi dialettici. Bollettino della Unione Matematica Italiana. Series IV, 9, 51–61.Google Scholar
Cellucci, C. (2000). The growth of mathematical knowledge: An open world view. In Grosholz, E. and Breger, H., editors. The Growth of Mathematical Knowledge. Dordrecht: Kluwer, pp. 153–176.CrossRefGoogle Scholar
Cooper, S. B. (2003). Computability Theory. Boca Raton, London, New York, Washington, DC: Chapman & Hall/CRC Mathematics.Google Scholar
Copeland, B. J., & Shagrir, O. (2013). Turing versus Gödel on computability and the mind. In Copeland, B. J., Posy, C. J., and Shagrir, O., editors. Computability: Turing, Gödel, Church, and Beyond. Cambridge, MA: MIT Press, pp. 1–33.CrossRefGoogle Scholar
Gnani, G. (1974). Insiemi dialettici generalizzati. Matematiche, XXIX(2), 1–11.Google Scholar
Gold, E. M. (1965). Limiting recursion. Journal of Symbolic Logic, 30, 28–48.Google Scholar
Hájek, P. (1977). Experimental logics and ${\rm{\Pi }}_3^0$ theories. Journal of Symbolic Logic, 42(4), 515–522.Google Scholar
Hintikka, J., & Mutanen, A. (1988). An alternative concept of computability. In Hintikka, J., editor. Language, Truth, and Logic in Mathematics. Dordrecht: Kluwer, pp. 174–188.Google Scholar
Jeroslow, R. G. (1975). Experimental logics and ${\rm{\Delta }}_2^0$ theories. Journal of Philosophical Logic, 4(3), 53–267.Google Scholar
Kelly, K. (1996). The Logic of Reliable Inquiry. Oxford: Oxford University Press.CrossRefGoogle Scholar
Kitcher, P. (1983). The nature of mathematical knowledge. New York: Oxford University Press.Google Scholar
Kreisel, G. (1967). Informal rigour and completeness proofs. In Lakatos, I., editor. Problems in the Philosophy of Mathematics. Amsterdam: North-Holland, pp. 138–171.CrossRefGoogle Scholar
Kugel, P. (1986). Thinking may be more than computing. Cognition, 32, 137–198.Google Scholar
Lakatos, I. (1976a). Proofs and Refutations. Cambridge: Cambridge University Press.Google Scholar
Lakatos, I. (1976b). A renaissance of empiricism in the recent philosophy of mathematics. British Journal for the Philosophy of Science, 27(3), 201–223.Google Scholar
Lolli, G. (2008). Experimental methods in proofs. In Lupacchini, R., and Corsi, G., editors. Deduction, Computation, Experiment. Milan: Springer, pp. 65–79.CrossRefGoogle Scholar
Magari, R. (1974). Su certe teorie non enumerabili. Annali di Matematica Pura ed Applicata. Series IV, XCVIII, 119–152.Google Scholar
Magari, R. (1980). Natura empirica della metamatematica. Technical report, Dipartimento di Matematica, Università di Siena.Google Scholar
Mancosu, P. (2008). The Philosophy of Mathematical Practice. Oxford: Oxford University Press.CrossRefGoogle Scholar
Montagna, F., Simi, G., & Sorbi, A. (1996). Logic and probabilistic systems. Archive for Mathematical Logic, 35(4), 225–261.Google Scholar
Osherson, D. N., Stob, M., & Weinstein, S. (1991). A Universal Inductive Inference Machine. Journal of Symbolic Logic, 56(2), 661–672.Google Scholar
Putnam, H. (1965). Trial and error predicates and the solution of a problem of Mostowski. Journal of Symbolic Logic, 30, 49–57.Google Scholar
Rogers, H. Jr. (1967). Theory of Recursive Functions and Effective Computability. New York: McGraw-Hill.Google Scholar
Shapiro, S., & Mc Carthy, T. (1987). Turing projectability. Notre Dame Journal of Formal Logic, 28(4), 520–537.Google Scholar
Soare, R. I. (1987). Recursively Enumerable Sets and Degrees. Perspectives in Mathematical Logic, Omega Series. Heidelberg: Springer-Verlag.Google Scholar
Turing, A. M. (1947). Turing Digital Archive. Lecture to London Mathematical Society, February 20, 1947.Google Scholar
Turing, A. M. (1996). Intelligent machinery, a heretical theory, c. 1951. Philosophia Mathematica. Series III, 4(3), 256–260.Google Scholar
van Leeuwen, J., & Wiedermann, J. (2012). Computation as an unbounded process. Theoretical Computer Science, 429, 202–212.CrossRefGoogle Scholar