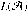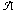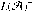Two deterministic finite automata are almost equivalent if they disagree in acceptance
only for finitely many inputs. An automaton A is hyper-minimized if no
automaton with fewer states is almost equivalent to A. A regular language
L is canonical if the minimal automaton accepting L is
hyper-minimized. The asymptotic state complexity
s∗(L) of a regular language
L is the number of states of a hyper-minimized automaton for a language
finitely different from L. In this paper we show that: (1) the class of
canonical regular languages is not closed under: intersection, union, concatenation,
Kleene closure, difference, symmetric difference, reversal, homomorphism, and inverse
homomorphism; (2) for any regular languages L1 and
L2 the asymptotic state complexity of their sum
L1 ∪ L2, intersection
L1 ∩ L2, difference
L1 − L2, and symmetric
difference L1 ⊕ L2 can be bounded
by
s∗(L1)·s∗(L2).
This bound is tight in binary case and in unary case can be met in infinitely many cases.
(3) For any regular language L the asymptotic state complexity of its
reversal LR can be bounded by
2s∗(L). This bound is tight
in binary case. (4) The asymptotic state complexity of Kleene closure and concatenation
cannot be bounded. Namely, for every k ≥ 3, there exist languages
K, L, and M such that
s∗(K) = s∗(L) = s∗(M) = 1
and
s∗(K∗) = s∗(L·M) = k.
These are answers to open problems formulated by Badr et al.
[RAIRO-Theor. Inf. Appl.43 (2009) 69–94].