Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
Hostname: page-component-66d7dfc8f5-cdn8t Total loading time: 0.916 Render date: 2023-02-09T11:01:03.081Z Has data issue: true Feature Flags: { "useRatesEcommerce": false } hasContentIssue true
  • English
RAIRO - Theoretical Informatics and Applications RAIRO - Theoretical Informatics and Applications

Article contents

Deciding whether a relation defined inPresburger logic can be defined in weaker logics

Published online by Cambridge University Press:  18 January 2008

Christian Choffrut
Christian Choffrut*
Affiliation:
LIAFA, Université de Paris 7, 2 place Jussieu, 75251 Paris Cedex 05; cc@liafa.jussieu.fr
Get access

Abstract

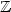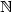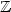We consider logics on $\mathbb{Z}$ and $\mathbb{N}$ which are weaker than Presburger arithmetic and we settle the following decision problem: given a k-ary relation on $\mathbb{Z}$ and $\mathbb{N}$ 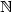which are first order definable in Presburger arithmetic, are they definable in these weaker logics? These logics, intuitively, are obtained by considering modulo and threshold counting predicates for differences of two variables.

Keywords

Presburger arithmeticfirst order logicdecidability
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 42 , Issue 1: A nonstandard spirit among computer scientists:a tribute to Serge Grigorieff at the occasion of his 60th birthday , January 2008 , pp. 121 - 135
Copyright
© EDP Sciences, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Carton, O., Choffrut, C. and Grigorieff, S.. Decision problems for rational relations. RAIRO-Theor. Inf. Appl. 40 (2006) 255–275. CrossRef
C. Choffrut and M. Goldwurm. Timed automata with periodic clock constraints. J. Algebra Lang. Comput. 5 (2000) 371–404.
S. Eilenberg. Automata, Languages and Machines, volume A. Academic Press (1974).
S. Eilenberg and M.-P. Schützenbeger. Rational sets in commutative monoids. J. Algebra 13 (1969) 173–191.
S. Ginsburg and E.H. Spanier. Bounded regular sets. Proc. Amer. Math. Soc. 17 (1966) 1043–1049.
M. Koubarakis. Complexity results for first-order theories of temporal constraints. KR (1994) 379–390.
H. Läuchli and C. Savioz. Monadic second order definable relations on the binary tree. J. Symbolic Logic 52 (1987) 219–226.
A. Muchnik. Definable criterion for definability in presburger arithmentic and its application (1991). Preprint in russian.
P. Péladeau. Logically defined subsets of ${\mathbb{N}}^k$ . Theoret. Comput. Sci. 93 (1992) 169–193.
J.-E. Pin. Varieties of formal languages. Plenum Publishing Co., New-York (1986). (Traduction de Variétés de langages formels.)
J. Sakarovitch. Eléments de théorie des automates. Vuibert Informatique (2003).
A. Schrijver. Theory of Linear and Integer Programming. John Wiley & sons (1998).
C. Smoryński. Logical Number Theory I: An Introduction. Springer Verlag (1991).

Save article to Kindle

To save this article to your Kindle, first ensure coreplatform@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Deciding whether a relation defined in Presburger logic can be defined in weaker logics
Available formats
×

Save article to Dropbox

To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.

Deciding whether a relation defined in Presburger logic can be defined in weaker logics
Available formats
×

Save article to Google Drive

To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.

Deciding whether a relation defined in Presburger logic can be defined in weaker logics
Available formats
×
×

Reply to: Submit a response

Please enter your response.

Your details

Please enter a valid email address.

Conflicting interests

Do you have any conflicting interests? *