Article contents
Communication Complexity and Lower Bounds on Multilective Computations
Published online by Cambridge University Press: 15 August 2002
Abstract
Communication complexity of two-party (multiparty) protocols
has established itself as a successful method for proving lower
bounds on the complexity of concrete problems for numerous computing
models. While the relations between communication complexity and
oblivious, semilective computations are usually transparent and
the main difficulty is reduced to proving nontrivial lower bounds on
the communication complexity of given computing problems, the
situation essentially changes, if one considers non-oblivious or
multilective computations. The known lower bound proofs for such
computations are far from being transparent and the crucial ideas
of these proofs are often hidden behind some nontrivial
combinatorial analysis. The aim of this paper is to create a general
framework for the use of two-party communication protocols for lower
bound proofs on multilective computations. The result of this
creation is not only a transparent presentation of some known lower
bounds on the complexity of multilective computations on distinct computing
models, but also the derivation of new
nontrivial lower bounds on multilective VLSI circuits and multilective planar Boolean
circuits.
In the case of VLSI circuits we obtain a generalization of
Thompson's lower bounds on AT2 complexity for multilective circuits.
The Ω(n2) lower bound on the number of gates of any k-multilective
planar Boolean circuit computing a specific Boolean function of n variables
is established for $k<\frac{1}{2} \log_2 n$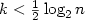 .
Another advantage of this framework is that it provides lower
bounds for a lot of concrete functions. This contrasts to the typical papers
devoted to lower bound proofs, where one establishes a lower bound for one
or a few specific functions.
.
Another advantage of this framework is that it provides lower
bounds for a lot of concrete functions. This contrasts to the typical papers
devoted to lower bound proofs, where one establishes a lower bound for one
or a few specific functions.
Keywords
- Type
- Research Article
- Information
- Copyright
- © EDP Sciences, 1999
References
- 2
- Cited by


