Article contents
Binary words avoiding the pattern AABBCABBA
Published online by Cambridge University Press: 11 February 2010
Abstract
We show that there are three types of infinite words over the two-letter
alphabet {0,1} that avoid the pattern AABBCABBA. These types, P, E0, and E1,
differ by the factor complexity and the asymptotic frequency of the letter 0.
Type P has polynomial factor complexity and letter frequency $\frac{1}{2}$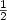 .
Type E0 has exponential factor complexity and the frequency of the letter 0 is at least
0.45622 and at most 0.48684. Type E1 is obtained from type E0 by exchanging 0 and 1.
.
Type E0 has exponential factor complexity and the frequency of the letter 0 is at least
0.45622 and at most 0.48684. Type E1 is obtained from type E0 by exchanging 0 and 1.
- Type
- Research Article
- Information
- RAIRO - Theoretical Informatics and Applications , Volume 44 , Issue 1: Special issue dedicated to the 12th "Journées Montoises d'Informatique Théorique" , January 2010 , pp. 151 - 158
- Copyright
- © EDP Sciences, 2010
References
- 2
- Cited by


