This paper is motivated by operating self service transport systems that flourish nowadays. In cities where such systems have been set up with bikes, trucks travel to maintain a suitable number of bikes per station. 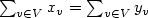It is natural to study a version of the C-delivery TSP defined by Chalasani and Motwani in which, unlike their definition, C is part of the input: each vertex v of a graph G=(V,E) has a certain amount xv of a commodity and wishes to have an amount equal to yv (we assume that $\sum_{v\in V}x_v=\sum_{v\in V}y_v$ and all quantities are assumed to be integers); given a vehicle of capacity C, find a minimal route that balances all vertices, that is, that allows to have an amount yv of the commodity on each vertex v. This paper presents among other things complexity results, lower bounds, approximation algorithms, and a polynomial algorithm when G is a tree.