1 INTRODUCTION
The Murchison Widefield Array (MWAFootnote 1 ) is a low-frequency radio telescope operating between 80 and 300 MHz. It is located at the Murchison Radio-astronomy Observatory (MRO) in Western Australia, the planned site of the future Square Kilometre Array (SKAFootnote 2 ) low-band telescope, and is one of three telescopes designated as a Precursor for the SKA. The MWA has been developed by an international collaboration, including partners from Australia, India, New Zealand, and the United States. It has begun operations in 2013. In this paper, we review the science capabilities of the telescope and the primary science objectives motivating its design and operation. Details of the technical design and specifications of the MWA as built are presented in a companion article (Tingay et al. Reference Tingay2013), which supersedes the earlier Lonsdale et al. (Reference Lonsdale2009) description of plans for the instrument.
The four key science themes driving the MWA are (1) searching for redshifted 21-cm emission from the epoch of reionisation (EoR) in the early Universe; (2) Galactic and extragalactic surveys; (3) time-domain astrophysics; and (4) solar, heliospheric, and ionospheric science and space weather. We describe the plans and objectives for each of the key science themes in Sections 2–5.
The frequency range targeted by the MWA is one of the more difficult portions of the spectrum for ground-based radio telescopes due to strong distortions of incoming signals by the Earth's ionosphere and also due to congested terrestrial communications, including FM radio, TV stations, aircraft navigation, and satellite communications. Hence, the low-frequency radio sky remains one of the least-explored domains in astronomy. The MRO site mitigates many issues associated with radio interference for the telescope, but processing of MWA observations requires particular care to correct for the ionospheric distortions.
The unifying design theme for the MWA is that of high survey efficiency. Many of the science goals require large areas of the sky to be surveyed and the EoR objective further requires very high surface brightness sensitivity. It was recognised early in the development of the MWA that arcminute angular resolution is a convenient balance between the opposing tensions of maximizing scientific returns and minimizing technical complexity. Arcminute angular scales are sufficient to probe typical ionised bubbles during the EoR, study diffuse and polarised emission structures in the Galaxy, reduce extragalactic source confusion, image bursts in the solar corona near the Sun's surface, and localise transient events with sufficient precision to allow follow-on searches at other wavelengths. In order to achieve arcminute resolution, the longest baseline of the MWA is 3 km. This distance is within the scale size of a typical isoplanatic patch in the ionosphere, allowing simplifying assumptions to be employed for widefield ionospheric calibration and keeping real-time imaging computations within reach of modest computer clusters.
The system properties of the MWA are described in detail by Tingay et al. (Reference Tingay2013). We summarise them here in Table 1. The time needed to reach a point source sensitivity of σs for the MWA is given by
Table 1 System parameters for the MWA.

a For frequency-dependent parameters, listed values are given at 150 MHz.
b Sky temperature varies considerably with Galactic latitude. Here, we use typical values from Nijboer, Pandey-Pommier, & de Bruyn (Reference Nijboer, Pandey-Pommier and de Bruyn2009) and Rogers & Bowman (Reference Rogers and Bowman2008).
The surface brightness sensitivity of the MWA varies significantly with angular scale. The MWA antenna layout emphasises a dense, central core in order to achieve a high surface brightness sensitivity on degree scales for EoR science. For a typical EoR spectral resolution of 1 MHz, the brightness temperature uncertainty is less than 150 mK after 1 h of integration on degree scales, whereas it is approximately 3 K on arcminute scales.
In the remainder of the paper, we discuss the four key science themes. Section 2 describes the EoR science. In Section 3, broad categories of radio astronomy science are discussed within the context of sky surveys. Section 4 describes the time-domain astronomy that will be possible with the MWA and Section 5 presents the primary solar, heliospheric, and ionospheric science goals. We conclude in Section 6.
2 EPOCH OF REIONISATION
One of the most significant events in the history of the intergalactic medium (IGM) was the reionisation of hydrogen. The EoR marks the time when the small fraction of matter within galaxies significantly affected their surroundings (and hence future generations of galaxies), ionising the intergalactic gas and heating it from tens of Kelvin to ~104 K.
The MWA has been designed with the goal of detecting 21-cm emission from the reionisation epoch. It is one of three new radio arrays specifically targeting this science objective, along with PAPERFootnote 3 and LOFAR.Footnote 4 The 21-cm hyperfine transition line of neutral hydrogen is anticipated to provide an ideal probe of reionisation. Its weak oscillator strength (in contrast to the Lyα line) allows 21-cm photons to propagate from fully neutral environments at high redshifts without appreciable absorption. This property makes it possible to directly observe the neutral hydrogen gas before and during reionisation.
Unlike the continuum emission of the cosmic microwave background (CMB), 21-cm emission contains information in the frequency (or redshift) dimension in addition to in angle, enabling the study of the full history of reionisation. Redshifted 21-cm emission from neutral hydrogen gas in the IGM should appear as a faint, diffuse background in radio frequencies below ν ≲ 200 MHz for redshifts above z > 6, where ν = 1420/(1 + z) MHz. At these redshifts, the expected unpolarised differential brightness temperature, δT 21, of the redshifted 21-cm line relative to the CMB is readily calculable from basic principles (see Furlanetto, Oh, & Briggs Reference Furlanetto, Oh and Briggs2006, for a complete review) and is given by
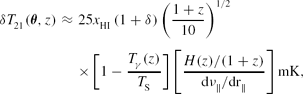 \begin{eqnarray}
\delta T_{21}({\bm{\theta}}, z) &\approx & 25 x_{\rm{H{I}}} \left(1+\delta \right) \left(\frac{1+z}{10} \right)^{1/2}\nonumber\\
&& \times \left[1 - \frac{T_{\gamma} (z)}{T_{\rm S}} \right] \left[\frac{H(z)/(1+z)}{\rm{d}\nu _{\|}/\rm{d}r_{\|}} \right] \rm{mK},
\end{eqnarray}
\begin{eqnarray}
\delta T_{21}({\bm{\theta}}, z) &\approx & 25 x_{\rm{H{I}}} \left(1+\delta \right) \left(\frac{1+z}{10} \right)^{1/2}\nonumber\\
&& \times \left[1 - \frac{T_{\gamma} (z)}{T_{\rm S}} \right] \left[\frac{H(z)/(1+z)}{\rm{d}\nu _{\|}/\rm{d}r_{\|}} \right] \rm{mK},
\end{eqnarray}
All of these factors contain unique astrophysical information. The dependence on δ traces the development of the cosmic web (Scott & Rees Reference Scott and Rees1990), while the velocity factor creates line-of-sight distortions that can be used to separate different components of the signal (Barkana & Loeb Reference Barkana and Loeb2005). The other two factors depend on the ambient radiation fields in the early Universe. The local neutral fraction, x HI, is determined by the ionising radiation emitted by galaxies and possibly quasars. Theoretical studies suggest that the distribution of neutral gas during reionisation is very inhomogeneous (e.g. McQuinn et al. Reference McQuinn, Lidz, Zahn, Dutta, Hernquist and Zaldarriaga2007). Finally, the 21-cm spin temperature, T S, is determined primarily by three mechanisms that affect the hyperfine level populations: the ambient radiation at 21 cm due to the CMB with T γ, the ultraviolet background that tends to drive T S to the gas temperature (Wouthuysen Reference Wouthuysen1952; Field Reference Field1958), and heating from the cosmological X-ray background (Chen & Miralda-Escudé Reference Chen and Miralda-Escudé2004). By the time the Universe is a few per cent ionised, most calculations predict that T S≫T γ, such that fluctuations in T S are not important (e.g. Furlanetto et al. Reference Furlanetto, Oh and Briggs2006).
Figure 1 illustrates how the factors in Equation (2) combine to create the observable 21-cm signal. The panels in this figure are from the simulations of McQuinn et al. (Reference McQuinn, Lidz, Zahn, Dutta, Hernquist and Zaldarriaga2007) and are 100 cMpc across or ~0.5° in angle (a small fraction of the ~20° MWA field of view). The left panel of Figure 1 shows the expected signal just before reionisation begins, when the fluctuations are dominated by local perturbations in the matter density. In the middle panel, reionisation is underway (x HI≈0.5), and the large-scale voids in the map signify ionised regions. After reionisation has largely finished (right panel), only localised pockets of neutral hydrogen remain.

Figure 1. Simulated 21-cm brightness temperature maps from simulation S1 by McQuinn et al. (Reference McQuinn, Lidz, Zahn, Dutta, Hernquist and Zaldarriaga2007) at three epochs calculated under the assumption that T S≫T γ. The left-hand panel is an almost fully neutral IGM (before reionisation at z = 12) such that the 21-cm emission traces the matter density. The middle panel is during reionisation (x HI≈0.5, which occurs at z = 8 in this simulation): the dark regions represent ionised regions around galaxies. Lastly, the right-hand panel shows the residual emission near the end of reionisation (z = 6). Each panel is 100 cMpc across and subtends 0.5° (a small fraction of the MWA field of view).
The MWA will attempt to probe structures in the redshifted 21-cm background in order to reveal the astrophysics of reionisation. The MWA is expected to be sensitive to the power spectrum of the 21-cm signal over the redshift range 6 < z ≲ 10 (Section 2.1). Its observations have the potential to characterise the nature of the sources that are responsible for ionising the IGM, chart the evolution of the global neutral fraction, and probe the nature of quasar emissions by constraining the properties of their ionised proximity zones.
2.1 21-cm power spectrum
Initial MWA observations aimed at detecting 21-cm emission will focus on two target regions at relatively high Galactic latitudes (see Figure 2). Over the course of one year, approximately 1000 h of optimal nighttime observations will be divided between these two regions. The signal-to-noise ratio (S/N) in each pixel will be ≲ 1, with the highest S/N on the largest angular modes. Hence, rather than imaging the 21-cm brightness temperature in the target fields, reionisation science with the MWA will focus on statistical measures of the 21-cm emission. The number of independent measurements in a raw, multi-frequency MWA data cube will be ~108. These samples record largely Galactic synchrotron and free–free emission (≳200 K) and extragalactic continuum sources (~50 K), with only a small contribution from the redshifted 21-cm signal (~25 mK). The primary approach planned for the MWA is to calculate the power spectrum of spatial fluctuations of the 21-cm signal.

Figure 2. Projected all-sky brightness temperature map of de Oliveira-Costa et al. (Reference de Oliveira-Costa, Tegmark, Gaensler, Jonas, Landecker and Reich2008) at 150 MHz. The primary (1) and secondary (2) target regions for EoR observations are centred at α, δ = 60°, −30° (ℓ, b = 228°, −49°) and α, δ = 155°, −10° (ℓ, b = 253°, + 38°), respectively. The solid white curves indicate the 50% response power contour of the primary antenna tile beams for reference and the dashed lines show the 10% power contour.
The three-dimensional power spectrum of redshifted 21-cm emission is the square of the Fourier transform of δT
21 (2). It has a large spherically symmetric component due to the isotropy of space, but has slightly more power for modes that point in the line-of-sight direction that results from peculiar velocities. The predicted components in the full three-dimensional power spectrum can be decomposed into terms with different powers of
![]() $\mu \equiv \hat{k}\,{\cdot}\,\hat{n}$
, where μ is the cosine of the angle between the line of sight and the wavevector (Kaiser Reference Kaiser1987; Barkana & Loeb Reference Barkana and Loeb2005; McQuinn et al. Reference McQuinn, Zahn, Zaldarriaga, Hernquist and Furlanetto2006). Thus,
$\mu \equiv \hat{k}\,{\cdot}\,\hat{n}$
, where μ is the cosine of the angle between the line of sight and the wavevector (Kaiser Reference Kaiser1987; Barkana & Loeb Reference Barkana and Loeb2005; McQuinn et al. Reference McQuinn, Zahn, Zaldarriaga, Hernquist and Furlanetto2006). Thus,
Averaging P 21( k ) over angle to yield P 21(k) loses some statistical information, but at the sensitivity of the MWA this loss is minor during reionisation. With one year of the planned observing programme, the MWA can constrain P 21(k) at a given redshift and across a range of scales spanning 0.01 ≲ k ≲ 1 cMpc−1 with total S/N ≈ 14 (Morales & Hewitt Reference Morales and Hewitt2004; Bowman, Morales, & Hewitt Reference Bowman, Morales and Hewitt2006; McQuinn et al. Reference McQuinn, Zahn, Zaldarriaga, Hernquist and Furlanetto2006; Beardsley et al. Reference Beardsley2013). The sensitivity of the MWA to the spherically averaged power spectrum is shown in Figure 3.

Figure 3. MWA thermal uncertainty at z = 8 with simulated 21-cm power spectra. The black stepped line is the 1σ thermal uncertainty modelled for a combined observation of the primary and secondary EoR fields with a total of 1 600 h (Beardsley et al. Reference Beardsley2013). The 21-cm curves are calculated using the fiducial simulation described by Lidz et al. (Reference Lidz, Zahn, McQuinn, Zaldarriaga and Hernquist2008). The power spectrum is very steep at the beginning of reionisation (x HI≳0.8) and falls rapidly at the scales probed by the MWA. Large-scale power returns as large ionised regions form by x HI≈0.5 and then it falls again with decreasing neutral fraction. The MWA should be able to detect the power spectrum at z = 8 for any appreciable neutral fraction outside of the range 0.95≳x HI≳0.8.
The properties of the power spectrum, P 21(k), during reionisation are dominated by the characteristics of the ionised bubbles (Figure 1, middle panel) that are determined by the ionising radiation produced by the first galaxies and quasars. Figure 3 illustrates how Δ21 ≡ (k 3 P 21(k)/2π2)1/2 contains information about the reionisation process. It plots Δ21 for the fiducial model of Lidz et al. (Reference Lidz, Zahn, McQuinn, Zaldarriaga and Hernquist2008) at several neutral fractions. The shape of the power spectrum evolves considerably as the hydrogen in the IGM becomes ionised, with power shifting from small scales initially, to larger scales later when large ionised bubbles have formed. Eventually, the amplitude decreases as hydrogen reionisation completes.
The sensitivity forecasts shown in Figure 3 utilise both the primary and secondary target fields in combination, assuming that each field has been observed over an 8-MHz bandwidth (corresponding to Δz ≈ 0.5). The full 32-MHz instantaneous bandwidth of the MWA will yield four such measurements spanning a contiguous redshift range of Δz ≈ 2. Initial observations will focus on the lower redshifts (6 < z < 8), where the sensitivity of the instrument is highest due to the lower sky temperature. Observations at low redshifts will crucially demonstrate whether the foreground subtraction is successful, since the quality of the foreground subtraction will be readily apparent at z < 6, where no 21-cm signal should be detectable by the MWA since x HI≲2% after reionisation (Wyithe & Loeb Reference Wyithe and Loeb2008).
2.1.1 Sources of reionisation
The 21-cm sky contains a wealth of information about the properties of the ionising sources because they strongly affect the topology of the EoR. Reionisation scenarios dominated by stars in galaxies produce well-defined ionised regions, while ‘miniquasars’ (small accreting black holes) yield more diffuse features (Zaroubi & Silk Reference Zaroubi and Silk2005) and reionisation processes involving decaying/annihilating dark matter particles would be very inhomogeneous (Belikov & Hooper Reference Belikov and Hooper2009). The 21-cm observations could even distinguish between different stellar reionisation scenarios (Lidz et al. Reference Lidz, Zahn, McQuinn, Zaldarriaga and Hernquist2008). For example, more massive galaxies produce larger ionised regions (Furlanetto, Zaldarriaga, & Hernquist Reference Furlanetto, Zaldarriaga and Hernquist2004; McQuinn et al. Reference McQuinn, Lidz, Zahn, Dutta, Hernquist and Zaldarriaga2007). If it is able to constrain the shape and evolution of the power spectrum, the MWA will reveal the nature of some of the first cosmological objects.
2.1.2 The neutral fraction
Existing observations have provided tantalising hints about reionisation, but even more unanswered questions. CMB observations find that the average redshift of reionisation is z = 10 ± 2 (Komatsu et al. Reference Komatsu2009), and quasar absorption spectra imply that the Universe was totally ionised by z = 6, one billion years after the big bang. In addition, several studies have interpreted the large saturated regions at z > 6 in these absorption spectra as evidence for the end of reionisation (e.g. Fan et al. Reference Fan2006), but this conclusion is disputed (Becker, Rauch, & Sargent Reference Becker, Rauch and Sargent2007; Mesinger Reference Mesinger2010).
Detection of the 21-cm power spectrum will yield measures of x Hi(z) through predictable features that depend on the neutral fraction. As evident in Figure 3, the intensity of 10 cMpc scale fluctuations in 21-cm brightness temperature briefly fades when reionisation begins and the first galaxies ionise the overdense regions within a couple of cMpc of them. Next, the ionised regions surrounding individual galaxies overlap, creating ~10 cMpc ionised regions and an increase in power on these scales. Finally, all of the fluctuations fade as these bubbles overlap, swallowing the neutral hydrogen that remains. Each of these trends can be used to disentangle x Hi(z).
For many possible sources that have been considered in the literature (such as galaxies, quasars, and mini-halos), the amplitude of the power spectrum peaks at x Hi ≈ 50%. The MWA could probe the global ionisation history by tracking the evolution of this amplitude and shape of the 21-cm power spectrum. Using these features, the volume-filling factor of neutral hydrogen (comparable to the mass-averaged neutral fraction) can be constrained after approximately two years of observations to between 0.4<x HI<0.75 at 2σ significance for the redshift where the power spectrum achieves its maximum amplitude (Lidz et al. Reference Lidz, Zahn, McQuinn, Zaldarriaga and Hernquist2008). While unlikely, it is possible that the IGM is highly ionised over the range of redshifts measured by the MWA. Lidz et al. (Reference Lidz, Zahn, McQuinn, Zaldarriaga and Hernquist2008) found that a null detection with the MWA at z ≤ 8 would be able to constrain the neutral fraction to ≲4%.
Observations of individual quasar H ii regions offer an additional probe of the global neutral hydrogen fraction since the contrast between the ionised H ii region and neutral IGM can provide a measurement of the neutral fraction at the redshift of the quasar. Geil et al. (Reference Geil, Wyithe, Petrovic and Oh2008) have found that the shape of the quasar H ii regions can be recovered from foreground subtracted MWA maps by using the entire data cube to help determine the contrast between the external IGM and ionised interior.
2.2 Quasar H ii regions
The detection of large quasar-generated H ii regions in redshifted 21-cm emission late in the EoR may be possible with the MWA (Wyithe, Loeb, & Barnes Reference Wyithe, Loeb and Barnes2005; Wyithe Reference Wyithe2008). Geil et al. (Reference Geil, Wyithe, Petrovic and Oh2008) have modelled the observation of quasar H ii regions in a partially ionised IGM. Figure 4 shows a simulated example of a recovered quasar H ii region with the MWA after approximately one observing season. The recovery is possible only for quasars with positions known a priori. Although the EoR fields will not overlap the Sloan Digital Sky Survey (SDSS) fields, where the existing known z ≈ 6 quasars reside, the contemporaneous SkyMapper optical survey (Keller et al. Reference Keller2007) should find around one quasar at z>6.25, and around 5 quasars at z>6 per MWA field.

Figure 4. Simulated recovery of a quasar H ii region in an evolving IGM, as observed by an MWA-like instrument (Geil et al. Reference Geil, Wyithe, Petrovic and Oh2008). Foregrounds were simulated and removed for the maps shown. The data cube is only a small part of a full MWA field and spans ~3.3° on a side and 33 MHz deep. The three panels show different slices through the centre of the box when viewed from the front, side, and top. Each slice is 6 cMpc thick, which corresponds to ~3 MHz along the x 3-axis. The extracted shape of the H ii region is shown, based on a nine-parameter model. The quasar was assumed to have a lifetime of 4 × 107 yr centred on z = 6.65 and to have produced an H ii region with a radius of 34 cMpc at that redshift. The mass-averaged IGM neutral fraction at the redshift of the quasar is ~15%.
Like all 21-cm signatures of the reionisation era, the detection of a quasar H ii region will need to overcome the difficulties associated with the removal of bright Galactic and extragalactic foregrounds. Geil et al. (Reference Geil, Wyithe, Petrovic and Oh2008) find that the primary effect of continuum foreground removal is to reduce contrast in the image. In particular, contributions to the 21-cm intensity fluctuations that have a scale length comparable to the frequency bandpass of the observation are removed by foreground subtraction. This loss of contrast, however, does not severely affect the ability of 21-cm observations to measure the size and shape of the H ii region. To demonstrate this quantitatively, Geil et al. (Reference Geil, Wyithe, Petrovic and Oh2008) modelled the H ii region shape as a spheroid described by six parameters and showed that the shape recovered following foreground removal agrees well with the shape derived directly from fitting using the input H ii region model.
Using the recovered best-fit shape of the H ii region, the global neutral fraction of hydrogen in the IGM can be measured directly from the contrast in intensity between regions that are within and beyond the H ii region. However, since foreground removal lowers the observed contrast between the H ii region and the IGM, such a measurement of the neutral fraction requires a correction factor. The value of this correction factor depends on the reionisation history and the polynomial used for foreground subtraction and can be accounted for using astrophysical models.
2.3 Non-Gaussian statistics
During the reionisation epoch, fluctuations in the 21-cm emission are expected to be highly non-Gaussian due to galaxy bias and the patchy structure imparted by the ionised bubbles in the IGM. The power spectrum (or two-point correlation function), therefore, is not a sufficient descriptor of the properties of the field, and additional statistical measures can provide complementary information. Several extensions to the power spectrum have been proposed in this context, including the 21-cm galaxy cross spectrum (Furlanetto et al. Reference Furlanetto, Oh and Briggs2006; Wyithe, Loeb, & Schmidt Reference Wyithe, Loeb and Schmidt2007; Lidz et al. Reference Lidz, Zahn, Furlanetto, McQuinn, Hernquist and Zaldarriaga2009), directly measuring the one-point probability distribution function (PDF) of the 21-cm brightness temperature distribution as a function of smoothing scale (Mellema et al. Reference Mellema, Iliev, Pen and Shapiro2006; Ichikawa et al. Reference Ichikawa, Barkana, Iliev, Mellema and Shapiro2010; Petrovic & Oh Reference Petrovic and Oh2011) or its higher moments (Wyithe & Morales Reference Wyithe and Morales2007), the three-point correlation function (bispectrum), matched filters (Datta et al. Reference Datta, Majumdar, Bharadwaj and Choudhury2008), the threshold clustering function, and other derived metrics (Barkana & Loeb Reference Barkana and Loeb2008).
2.4 Foreground subtraction
The ability of the MWA to achieve its reionisation science is entirely contingent on the successful separation of the 21-cm signal from astrophysical foregrounds. Hence, developing and demonstrating the techniques required to subtract foregrounds is a critical research objective.
2.4.1 Reference pipeline
The baseline foreground subtraction strategy is a multi-stage process consisting of the following principal stages:
1. Bright source subtraction. The first step in foreground subtraction is the removal of bright points sources. This is necessary because the sidelobes of these sources mask the 21-cm signal. Recent theoretical studies have indicated that bright point source subtraction must be complete for sources with flux greater than S ≳ 100 mJy in order to allow for successful subsequent Galactic continuum foreground subtraction (Liu, Tegmark, & Zaldarriaga Reference Liu, Tegmark, Bowman, Hewitt and Zaldarriaga2009). The brightest sources in the field will be ‘peeled’ (self-calibrate and subtract) from the raw visibility measurements (Mitchell et al. Reference Mitchell, Greenhill, Wayth, Sault, Lonsdale, Cappallo, Morales and Ord2008). Efficient techniques to remove point sources from gridded and integrated maps are also under investigation (Pindor et al. Reference Pindor, Wyithe, Mitchell, Ord, Wayth and Greenhill2011; Bernardi et al. Reference Bernardi, Mitchell, Ord, Greenhill, Pindor, Wayth and Wyithe2011).
2. Diffuse continuum subtraction. A variety of mechanisms contribute to diffuse continuum emission in the low-frequency radio sky including Galactic synchrotron emission, Galactic free–free emission, extragalactic free–free emission, and a sea of faint extragalactic point sources that are too numerous to identify individually in maps and are, thus, said to be ‘confused’. All of these foregrounds are significantly stronger than the redshifted 21-cm signal and have considerable angular structure on the sky (see Figure 2; Santos, Cooray, & Knox Reference Santos, Cooray and Knox2005, their Figure 5). But the emission mechanisms of these foregrounds produce smooth spectra that follow power-law profiles, making them possible to separate from the redshifted 21-cm emission by their long spectral coherence scales compared with the small, ~1-MHz spectral coherence of the reionisation signal. A variety of techniques have been proposed to accomplish this separation including polynomial fits along the spectral axis of each pixel in an image map or its uv-map conjugate, Minkowsky functionals, and non-parametric techniques. The baseline approach planned for the MWA is to fit and subtract a third-order polynomial from each pixel in the uv-domain representations of the bright source cleaned maps. This technique has been demonstrated for the MWA in the limit of perfect instrumental calibration (Liu et al. Reference Liu, Tegmark, Bowman, Hewitt and Zaldarriaga2009a; Bowman, Morales, & Hewitt Reference Bowman, Morales and Hewitt2009; Liu et al. Reference Liu, Tegmark, Bowman, Hewitt and Zaldarriaga2009b).

Figure 5. Polarised intensity at Faraday depth zero at 189 MHz from the MWA development system (Bernardi et al. Reference Bernardi2013). The field spans 2 400 deg2 with 15-arcmin angular resolution and is roughly centred on the southern Galactic pole, extending to within 20° of the Galactic plane. The radial lines are Galactic latitude and the circular arcs indicate Galactic longitude. Flux density is plotted on a linear colour scale from 0 to 0.2 Jy beam−1 RMSF−1 (white to black), where RMSF is the RM spread function. Polarised maps from the MWA showing similar complex structures and discontinuities that often have no counterparts in total intensity will be used to determine the properties of both ordered and turbulent magnetic fields in the Milky Way's ISM (see Figure 6).
3. Polarised leakage subtraction. In addition to the foreground issues discussed thus far, gain and phase calibration errors and non-ideal feeds conspire to contaminate all Stokes parameters further. This leakage leads to some portion of the complex linear polarisation signal finding its way into the Stokes I intensity maps that will be used for the redshifted 21-cm measurements. By using rotation measure (RM) synthesis (Brentjens & de Bruyn Reference Brentjens and de Bruyn2005; see also Section 3.3) to exploit the Fourier relationship between the polarised signal and the Faraday dispersion function, it is possible to identify components of the polarised signal with specific Faraday depth. The three-dimensional Stokes I data set is first re-sampled along the frequency axis into the natural λ2-basis for Faraday rotated emission. A one-dimensional Fourier transform is then applied along each line of sight. Any feature observed with a non-zero Faraday depth in the three-dimensional RM synthesis map will, by definition, be polarised contamination. By applying an inversion process together with knowledge of the instrument's specific leakage behaviour, this contamination can be subtracted (Geil, Gaensler, & Wyithe Reference Geil, Gaensler and Wyithe2011).
4. Statistical template fitting and power spectrum estimation. Many classes of errors and residuals remaining in the maps after the foreground cleaning stages described above can be modelled given sufficient knowledge of the instrumental response (Morales, Bowman, & Hewitt Reference Morales, Bowman and Hewitt2006; Bowman et al. Reference Bowman, Morales and Hewitt2009; Datta, Bowman, & Carilli Reference Datta, Bowman and Carilli2010; Morales et al. Reference Morales, Hazelton, Sullivan and Beardsley2012). The statistical properties of these residuals can be exploited to provide an additional layer of foreground removal by fitting templates of the residual statistical structures during the final redshifted 21-cm power spectrum parameter estimation. This technique is now commonly employed in CMB power spectrum analysis to account for the angular power of faint point sources and the effects of gravitational lensing.
2.4.2 Unified parameter estimation
The stages of foreground subtraction outlined above can be performed discretely, resulting in a series of output products, the last of which is used as the input into power spectrum estimation and other statistical tests to extract information from the redshifted 21-cm signal. Alternatively, they can be performed in a unified matrix framework that simultaneously fits models for the foreground contributions and the 21-cm statistical signal (Liu & Tegmark Reference Liu and Tegmark2011; Tegmark Reference Tegmark1997). The latter has the advantage of producing an optimal result that minimizes both bias (from thermal noise and foreground contamination) and correlations between parameters, and yields the smallest possible error bars, but at the expense of a large computational overhead. Advances in processing power and new efforts at sparse matrix reduction have begun to enable the trial application of unified parameter estimation in simulations and preliminary data, and it is expected this approach will ultimately be the preferred technique for data analysis.
3 GALACTIC AND EXTRAGALACTIC SCIENCE
The MWA offers several exciting science opportunities under the collective banner ‘Galactic and Extragalactic’ science. The major input into this science will come from a deep all-sky southern hemisphere survey over the MWA frequency range with full polarimetry and spectral resolution. This survey is a critical undertaking as it will also be used by the other science programmes as a basis for an all-sky foreground model and the identification of calibrators. The data will also be combined with other new surveys, including GALFACTS and POSSUM (1.4 GHz), S-PASS (2.4 GHz), and Planck (27 GHz to 1 THz) surveys.
The following sections describe a selection of Galactic and extragalactic experiments for which the MWA is well suited. These projects capitalise on three advantages of the MWA's low observing frequencies: (1) non-thermal sources will be very bright; (2) Faraday rotation (FR) and depolarisation will be very strong; and (3) along some sightlines free–free absorption will be significant.
3.1 The cosmic web
Theory suggests that the infall of baryons into the cosmic web results in high Mach number intergalactic shocks (e.g. Cen & Ostriker Reference Cen and Ostriker1999; Ryu et al. Reference Ryu, Kang, Hallman and Jones2003). When combined with seed magnetic fields, efficient cosmic ray acceleration is possible, resulting in steep-spectrum synchrotron emission (Keshet, Waxman, & Loeb Reference Keshet, Waxman and Loeb2004; Pfrommer et al. Reference Pfrommer, Springel, Enßlin and Jubelgas2006; Pfrommer, Enßlin, & Springel Reference Pfrommer, Enßlin and Springel2008; Skillman et al. Reference Skillman, Hallman, O'Shea, Burns, Smith and Turk2011; Araya-Melo et al. Reference Araya-Melo, Aragón-Calvo, Brüggen and Hoeft2012). This may be a ubiquitous component of the extragalactic radio sky (Keshet et al. Reference Keshet, Waxman and Loeb2004), and recent simulations suggest that the majority of the luminous radio shocks can be found in the outskirts of massive galaxy clusters (Araya-Melo et al. Reference Araya-Melo, Aragón-Calvo, Brüggen and Hoeft2012). The MWA's centrally condensed antenna configuration provides the theoretical sensitivity required to make the maps of this relativistic cosmic web. However, the accurate subtraction of discrete sources requires long baselines and high image fidelity (Brown Reference Brown2011). This may limit direct to the densest portions of the web, though statistical detection may be possible (Keshet et al. Reference Keshet, Waxman and Loeb2004; Brown, Farnsworth, & Rudnick Reference Brown, Farnsworth and Rudnick2010).
3.2 Radio relics and clusters
The MWA is also well suited for studying the diffuse, steep-spectrum synchrotron emission from clusters of galaxies. These objects, which include the centrally located ‘radio halos’ and peripheral ‘radio relics’ (Kempner et al. Reference Kempner, Blanton, Clarke, Enßlin, Johnston-Hollitt, Rudnick, Reiprich, Kempner and Soker2004), are probes of relativistic electrons and large-scale magnetic fields in the intra-cluster medium (ICM; Ferrari et al. Reference Ferrari, Govoni, Schindler, Bykov and Rephaeli2008; Rudnick et al. Reference Rudnick2009). Possible mechanisms for accelerating the cosmic-ray electrons responsible for this emission are turbulent re-acceleration following a cluster merger (Brunetti et al. Reference Brunetti, Setti, Feretti and Giovannini2001; Petrosian Reference Petrosian2001) and hadronic collisions between cosmic-ray and thermal protons (Dennison Reference Dennison1980; Blasi & Colafrancesco Reference Blasi and Colafrancesco1999). Low-frequency observations of clusters can probe these different models (Cassano et al. Reference Cassano, Brunetti, Röttgering and Brüggen2010, Reference Cassano, Brunetti, Norris, Röttgering, Johnston-Hollitt and Trasatti2012). The MWA's surface-brightness sensitivity will enable it to detect very steep-spectrum halos and relics. Predictions for the number of such halos and relics detectable with other low-frequency instruments are in the range of several hundred out to z < 0.6 (Cassano et al. Reference Cassano, Brunetti, Norris, Röttgering, Johnston-Hollitt and Trasatti2012).
At 150 MHz, the MWA will resolve 1-Mpc structures out to a redshift of 0.2 and 500 kpc structures out to z < 0.07. As with the detection of the cosmic web, confusion will be the major obstacle. Use of complementary higher resolution observations to model and subtract confusing sources will be required (Brown Reference Brown2011). The TIFR GMRT Sky Survey (TGSS) that covers 32 000 deg2 north of declination −30° with angular resolution 20 arcsec presents a good comparison survey to the MWA for this work.
3.3 Faraday tomography and magnetic fields
The Milky Way and most other spiral galaxies all show well-organised, large-scale magnetic fields, but the processes that amplify and maintain these fields are still not understood. On smaller scales, fluctuations in these magnetic fields regulate the dissipation of large-scale gas flows via a turbulent cascade. However, it is as yet unclear what processes generate turbulence in the interstellar medium (ISM), and how the subsequent spectrum and outer scale of turbulence depend on the surrounding conditions.
Polarised radio waves experience FR when they propagate through a magnetised plasma. The amount of rotation depends on the square of the wavelength, and on the path integral of n e B || along the line of sight (where n e is the electron density of the ISM, and B || is the magnetic field strength parallel to the line of sight). By exploiting this phenomenon, the MWA will provide a new view of the large- and small-scale properties of otherwise unobservable magnetic fields in the Milky Way.
At the low observing frequencies of the MWA, small RMs have substantial effects on the distribution of polarised emission from the sky. This emission directly traces invisible foreground magnetic fields, which imprint their structure on the smooth polarised synchrotron emission from the Milky Way via foreground FR. By imaging the polarised sky at a range of frequencies, the MWA will provide direct measurements of the turbulent cascade in the local ISM, and will reveal the detailed magnetic geometries of discrete large-scale structures such as the Local Bubble, the North Polar Spur, and the Magellanic Clouds. Using the high spectral resolution of the MWA, we can also apply RM synthesis techniques (see also Section 2.4.1) to isolate overlapping RM components. An example is provided in Figure 5, which shows the turbulent pattern seen at 189 MHz in a large region of the sky. The MWA will provide a unique tomographic view of magneto-ionised gas, allowing the identification of multiple emitting and rotating regions along the same line of sight.
The MWA is expected to make the largest contributions to Galactic science by observing at mid- and high-latitude regions. Depolarisation is already severe in the inner Galactic plane at 1.4 GHz (Reich, Reich, & Fuerst Reference Reich, Reich and Fuerst1990; Wolleben et al. Reference Wolleben, Landecker, Reich and Wielebinski2006; Haverkorn et al. Reference Haverkorn, Gaensler, McClure-Griffiths, Dickey and Green2006) and it is likely that much of the inner Galactic plane will appear completely depolarised below 300 MHz, although Bernardi et al. (Reference Bernardi2009) have detected polariased emission at arcminute scales at 150 MHz. Regions at mid and high latitudes, on the other hand, show considerable diffuse Galactic polarised structure at 350 MHz (Haverkorn, Katgert, & de Bruyn Reference Haverkorn, Katgert and de Bruyn2003b; de Bruyn et al. Reference de Bruyn, Katgert, Haverkorn and Schnitzeler2006; Schnitzeler, Katgert, & de Bruyn Reference Schnitzeler, Katgert and de Bruyn2009). The high sensitivity of the MWA to extended structure will enable it to map the diffuse polarised emission down to very low intensities, thus making visible weak Galactic magnetic fields in the local ISM and Galactic extended disc and halo that are undetectable at higher frequencies. RM synthesis across the entire MWA frequency band will result in an RM resolution of 0.3 rad m−2, which gives unprecedented detail in RM structure, allowing detailed studies of e.g. interstellar magnetised turbulence or magnetism in old supernova remnants. Increasing depolarisation as a function of decreasing frequency will give independent measurements of the amount and scale of fluctuations in the magneto-ionised medium (Sokoloff et al. Reference Sokoloff, Bykov, Shukurov, Berkhuijsen, Beck and Poezd1998; Gaensler et al. Reference Gaensler, Dickey, McClure-Griffiths, Green, Wieringa and Haynes2001).
A powerful new additional probe of the magnetised ISM comes from the polarisation gradient, in which the spatial derivatives of Stokes Q and U are combined to reveal locations on the sky at which the electron density or magnetic field strength show sharp fluctuations (Gaensler et al. Reference Gaensler2011). Application of the polarisation gradient at higher frequencies reveals a complex tangled network of narrow filaments (see Figure 6). These structures are a superset of the ‘polarisation canals’ seen in many radio polarisation images (Haverkorn & Heitsch Reference Haverkorn and Heitsch2004; Fletcher & Shukurov Reference Fletcher, Shukurov, Miville-Deschênes and Boulanger2007; Schnitzeler et al. Reference Schnitzeler, Katgert and de Bruyn2009), and directly reveal the locations of shocks, cusps, and shear in the turbulent ISM. The calculation of the polarisation gradient for magnetohydrodynamic simulations of interstellar turbulence shows that the intensity, alignment, and morphology of these filaments depend sensitively on input parameters such as the sonic Mach number and magnetic field strength (Burkhart, Lazarian, & Gaensler Reference Burkhart, Lazarian and Gaensler2012). By applying statistical metrics such as the genus and kurtosis, one can directly compare observations of the polarisations gradient with a grid of simulations, and thereby extract quantitative information on the otherwise unobservable turbulent parameters of the ISM.

Figure 6. Gradient image of linear polarisation, |∇P|, for an 18-deg2 region of the Southern Galactic Plane Survey (Gaensler et al. Reference Gaensler2011) that has been used to study magnetised turbulence in the ISM. Similar statistical techniques will be applied to MWA polarised maps to investigate magnetic field strength, Mach number, Reynolds number, and other properties in the ISM.
Two effects distinguish the applicability of this technique for MWA data. First, the ‘polarisation horizon’ (Uyaniker et al. Reference Uyaniker, Landecker, Gray and Kothes2003) at the MWA's low observing frequencies is very nearby (~100 pc, depending on observing frequency and Galactic coordinates; Bernardi et al. Reference Bernardi2013), meaning that we can probe small-scale local features. Second, the change in electron density or magnetic field strength needed to produce a fluctuation in Q or U is very small (since the amount of FR is proportional to λ2). For these two reasons, application of the polarisation gradient to MWA data should provide a detailed view of turbulence in the solar neighbourhood, and will be able to extend studies of the global turbulent cascade to smaller amplitudes and smaller angular scale than has been possible from previous observations.
RMs from extragalactic polarised point sources can be used to probe the intervening medium between the source and the observer, where generally the Galactic RM component dominates. Little is known about the polarisation percentages of extragalactic point sources at low frequencies. At 1.4 GHz, the expected number of linearly polarised sources down to a 3σ sensitivity of 1 mJy is about 1.2 × 104 per steradian (Beck & Gaensler Reference Beck and Gaensler2004). The number of polarised sources may decrease at low frequencies due to increased internal depolatisation. At 1.4 GHz, Mesa et al. (Reference Mesa, Baccigalupi, De Zotti, Gregorini, Mack, Vigotti and Klein2002) found a median polarisation fraction of 2.2% for sources above 80 mJy in the NVSS and Taylor, Stil, & Sunstrum (Reference Taylor, Stil and Sunstrum2009) have compiled a catalogue from the NVSS of over 30 000 polarised sources detected at better than 8σ and selected for polarisation fraction larger than 0.5%. The average polarisation fraction of sources in this catalogue is ~7%. At 350 MHz, Schnitzeler et al. (Reference Schnitzeler, Katgert and de Bruyn2009) found an average polarisation fraction of 3% for polarised sources brighter than 3 mJy (see also Haverkorn, Katgert, & de Bruyn Reference Haverkorn, Katgert and de Bruyn2003b). Bernardi et al. (Reference Bernardi2013) have surveyed 2 400 deg2 at 189 MHz using the 32-element MWA development system. They achieved noise levels of 15 mJy in polarisation and found only one polarised source, PMN J0351–;2744, which had a polarisation fraction of 1.2% and an RM of +34 rad m−2. The source was detected at 20σ. They also placed an upper limit of ~1% on the polarisation fraction of over 100 other bright sources above 4 Jy and detected diffuse polarised emission from the Galaxy with a peak level of 13 K.
Beam depolarisation is likely to be partially responsible for the lack of detected sources by Bernardi et al. (Reference Bernardi2013) since the MWA demonstrator had only 15-arcmin resolution. Using 1% polarisation fraction as a lower limit, along with source flux counts from the 6C survey (Hales, Baldwin, & Warner Reference Hales, Baldwin and Warner1988) and the ratio of polarised sources to unpolarised sources of 14% found by Banfield et al. (Reference Banfield, George, Taylor, Stil, Kothes and Scott2011), we estimate the number of sources that will be detectable by the MWA assuming a fiducial sensitivity of 1 mJy to be approximately ~1 source per square degree. These extragalactic source RMs will provide a ‘grid’ (Beck & Gaensler Reference Beck and Gaensler2004; Taylor et al. Reference Taylor, Stil and Sunstrum2009) that can be used to model large-scale magnetic fields in the Milky Way and, if deeper observations can provide a sufficiently dense grid, in nearby galaxies. Provided that polarisation calibration is accurate enough, the MWA will observe point-source RM values with superb precision.
3.4 The magellanic clouds
The Magellanic System, consisting of the Large Magellanic Cloud (LMC), Small Magellanic Cloud (SMC), and other components such as the Magellanic Stream and the Bridge and Leading Arm, is the Milky Way's most significant neighbour. The Clouds and the Milky Way are engaged in a three-body interaction, allowing us to study at close hand the effect of dynamical interaction processes on the physical structure, star formation, magnetic fields, and chemistry of such galaxies. The location of the Clouds in the deep southern sky makes them ideal candidates to observe with the MWA in preparation for much more detailed studies at similar frequencies with the SKA.
A comparison of radio and far-infrared (FIR) emission in the Magellanic Clouds and other nearby galaxies allows for a more detailed study of the correlation of cosmic rays, magnetic fields, and star formation than is possible for distant galaxies. At GHz frequencies, ATCA and IRAS studies allowed Hughes et al. (Reference Hughes, Wong, Ekers, Staveley-Smith, Filipovic, Maddison, Fukui and Mizuno2006) to find that the radio/FIR relation breaks down at ~50 pc (3 arcmin). Residual correlation at smaller scales remains due to the thermal component of the radio emission. Low-frequency observations of 6C galaxies have shown that the radio/FIR correlation remains good at 151 MHz (Fitt et al. 1988). Such observations are useful for further separating thermal and non-thermal sources of emission, for the study of synchrotron spectral aging and cosmic-ray diffusion, and for allowing k-corrections in cosmological studies.
The Magellanic Clouds are among only a handful of galaxies where the magnetic field can be studied via both FR of the polarised emission from background sources (sensitive to the line-of-sight field) and the polarised component of the diffuse emission (sensitive to the field direction in the plane of the sky). Studies of the Clouds at GHz frequencies (Haynes et al. Reference Haynes, Murray, Klein and Wielebinski1986; Gaensler et al. Reference Gaensler, Haverkorn, Staveley-Smith, Dickey, McClure-Griffiths, Dickel, Wolleben, Chyzy, Otmianowska-Mazur, Soida and Dettmar2005a; Mao et al. Reference Mao, Gaensler, Stanimirović, Haverkorn, McClure-Griffiths, Staveley-Smith and Dickey2008) have been useful in determining field strengths and morphology. Low-frequency observations will contribute by locating regions, perhaps associated with wind-blown superbubbles, of warm ionised gas unseen in X-rays, and by allowing more detailed studies of Faraday structures. The MWA will investigate the existence of a possible pan-Magellanic magnetic field via the old relativistic electron population which will have travelled far from its source.
3.5 Cosmic-ray mapping
One of the most exciting possibilities of the MWA survey at the lowest frequencies is the mapping of the three-dimensional cosmic-ray emissivity of the Milky Way. Within the MWA frequency range below approximately 200 MHz, Galactic H ii regions turn optically thick, blocking emission from the synchrotron background of the Galaxy. Typical optical depths of H ii regions are expected to be τ ≈ 2–5. These H ii regions, therefore, appear in absorption relative to the surroundings and the residual surface brightness at these positions allows a direct measurement of the integrated emissivity of cosmic-ray electrons out to the H ii region.
Nord et al. (Reference Nord, Henning, Rand, Lazio and Kassim2006) used 74-MHz VLA observations of H ii regions to detect such absorption against the Galactic synchrotron background. They found 92 regions with absorption features, 42 of which have measured distances. While such features have been seen since the 1950s, previous observations had poor resolution. The 10-arcmin VLA beam allowed for better spatial resolution while still remaining sensitive to low surface brightness. A number of surveys at higher frequencies have been conducted. Paladini et al. (Reference Paladini, Burigana, Davies, Maino, Bersanelli, Cappellini, Platania and Smoot2003) have compiled a catalogue of 1 442 diffuse and compact H ii regions based on 24 prior surveys, although a number of regions are omitted in their catalogue due to their emphasis on regions of the order of 10 arcmin (for an example of more recent identifications, see Bania et al. Reference Bania, Anderson, Balser and Rood2010). Approximately 800 of these regions have radio line velocity measurements providing distances. Paladini, Davies, & De Zotti (Reference Paladini, Davies and De Zotti2004) report on the distribution of the H ii regions, most of which have Galactic latitude within ±2° of the plane and are distributed throughout the disc, with the spiral arm structure of the Galaxy evident in their distribution.
Because many Galactic H ii regions have well-constrained distance estimates, MWA measurements of the synchrotron absorption features will allow for a three-dimensional map of the relativistic gas content in the Milky Way (e.g. Sun et al. Reference Sun, Reich, Waelkens and Enßlin2008). For H ii regions with kinematic distance degeneracies, MWA detections may be able to break the ambiguities. Since the MWA will have a view of the inner and outer Galaxy, it can provide the first accounting of the overall distribution of Galactic cosmic rays and of the large-scale magnetic fields that cause them to emit. In addition, due to its ability to measure the absorption in H ii regions as a function of frequency, the MWA should be able to yield the cosmic-ray electron emissivity spectrum in the direction of the H ii regions. As noted by Nord et al. (Reference Nord, Henning, Rand, Lazio and Kassim2006), multi-frequency observations should lead, therefore, to the mapping of the emissivity spectrum of cosmic rays.
Combined with the MWA's expected ability to detect and characterise supernova remnants (described below), these measurements will open new probes into the full energy budget of the Galaxy, including the role of supernovae in the production of energetic cosmic rays, as well as the diffusion and aging of the cosmic rays.
3.6 Galactic supernova remnants
Statistical studies of supernova rates suggest that there should be ~1000–2000 supernova remnants (SNRs) in our Galaxy (Li et al. Reference Li, Wheeler, Bash and Jefferys1991; Tammann, Loeffler, & Schroeder Reference Tammann, Loeffler and Schroeder1994), in stark contrast to the ~300 SNRs currently known (Green Reference Green2004; Brogan et al. Reference Brogan, Gelfand, Gaensler, Kassim and Lazio2006). This deficit is likely due to the observational selection effects, which discriminate against the identification both of old, faint, large SNRs, and young, small SNRs. The discovery of these ‘missing’ SNRs, and hence a characterisation of the full SNR population, is crucial for understanding the production and energy density of Galactic cosmic rays and the overall energy budget of the ISM.
Recent studies have demonstrated that low-frequency interferometric maps are a very efficient way of identifying new SNRs, because of the comparatively steep radio spectra of these systems. Most notable has been the survey of Brogan et al. (Reference Brogan, Gelfand, Gaensler, Kassim and Lazio2006), shown in Figure 7, which tripled the number of known SNRs in a 40-deg2 patch of the Galactic plane. The MWA will have a unique view of virtually all the inner Galaxy. The high-quality images that we expect to derive, across a range of frequencies, will provide a superb data set from which to identify hundreds of previously unidentified SNRs. Additionally, attempts to uncover old, faint sources will be enhanced by the development of new detection algorithms which we plan to implement on MWA data (e.g. circle Hough transforms; see Hollitt & Johnston-Hollitt Reference Hollitt and Johnston-Hollitt2012). These sources will be of interest both as a statistical ensemble and because among them will be individual objects with unique or extreme properties.

Figure 7. A 330-MHz panorama of part of the Galactic first quadrant, derived by smoothing VLA data from Brogan et al. (Reference Brogan, Gelfand, Gaensler, Kassim and Lazio2006) to 3-arcmin resolution. At these low observing frequencies, most of the bright sources correspond to non-thermal emission from SNRs. The MWA will be able to carry out such observations over almost the entire inner Galaxy.
3.7 Radio recombination lines
Low-frequency radio recombination lines (RRLs) are a sensitive tool for probing interstellar plasma. Below 100 MHz, carbon RRLs have been detected, but only in absorption, indicating an association with cold (<50 K) neutral gas or molecular clouds. At frequencies above 100 MHz, both carbon and hydrogen recombination lines have been observed, with the hydrogen lines likely associated with normal H ii regions as at higher frequencies. Both carbon and hydrogen lines have been found in observations along the Galactic plane as far as ±4° off the plane in Galactic latitude.
Measurements of RRLs in the MWA frequency range will provide an opportunity to study both emission and absorption processes. They will enable new studies of diffuse photodissociation zones that lie between molecular clouds and the general ISM and yield estimates for electron temperature and density in these regions. Carbon RRLs at 75 MHz exhibit a line-width range from 5 to 50 km s−1 (Erickson, McConnell, & Anantharamaiah Reference Erickson, McConnell and Anantharamaiah1995), corresponding to 1–12 kHz. Although, the MWA spectral resolution is not ideal for such narrow lines, single-pixel RRL observations have previously been used with much success (Alves et al. Reference Alves, Davies, Dickinson, Calabretta, Davis and Staveley-Smith2012). Sensitivity can also be regained by stacking different transitions within the observing band.
4 TIME-DOMAIN ASTROPHYSICS
The systematic exploration of the time domain is becoming a dominant frontier in astronomy, and significant resources have been deployed across the electromagnetic spectrum in order to probe and understand transient and time-variable phenomena. Radio transients vary on time scales ranging from less than one second to many days. The sources are compact objects or energetic/explosive events, and each type is being investigated at the forefront of astrophysics.
Radio observations can provide keys to understanding the explosive and transient Universe by directly measuring the effects of magnetic fields and non-thermal processes that drive the outbursts (e.g. Cordes, Lazio, & McLaughlin Reference Cordes, Lazio and McLaughlin2004). Even more intriguingly, synergies with multi-messenger astronomy (correlating electromagnetic transients with events detected in gravitational waves or neutrinos) have the potential to unlock substantial new physics. The MWA spans the upper frequencies associated with coherent radio sources and the lower frequencies of non-thermal magnetohydrodynamic processes. This makes observations of transients with the MWA particularly useful for understanding the non-equilibrium processes that drive dynamic astrophysical systems.
The potential sources of radio transient emission fall into five broad categories: coronal emission from nearby stars/substellar objects, emission from compact objects such as neutron stars and accreting black holes, explosive events such as gamma-ray bursts (GRBs) and radio supernovae, planetary emission from nearby systems, and new phenomena discovered through the opening of new regions of observational phase space. Of these, the first three are known sources of transient radio emission (at least at some frequencies), while the last two categories constitute more speculative targets. However, there are firm theoretical expectations that these latter objects should give rise to transient radio emission, and our searches will be far deeper than previous surveys.
First, we discuss in detail some of the expected physical constraints to be gained from the MWA observations of known sources of transients (Section 4.1). We then explore some of the more speculative science targets that we hope to explore with the new phase space opened up by the MWA (Section 4.2). We describe the new capabilities afforded by the MWA in Section 4.3 and in Section 4.4 we discuss observations of pulsars, which can be both steady and transient sources.
4.1 Known transient targets
4.1.1 Low-mass stars and brown dwarfs
Magnetised plasmas in stellar coronae (the outer layers of a star's magnetosphere) produce strong radio emission through non-thermal, collective, and/or coherent processes. This emission reflects local properties such as density and magnetic field strength and can be used to understand magnetic field generation, magnetospheric structure, angular momentum evolution, magnetic flaring mechanisms, and accretion processes. Furthermore, magnetic fields provide one of the few indirect probes of stellar interiors.
While radio studies of late-type stars and active binaries are well established (see Güdel Reference Güdel2002 for a review), radio observations of the lowest mass stars and brown dwarfs—objects incapable of sustained core hydrogen fusion (Kumar Reference Kumar1962)—have only recently been demonstrated and comprise a relatively new tool in this active field of research. M dwarfs with masses 0.1–0.5 M⊙ are a dominant stellar component of the Galaxy, comprising ~70% of all stars. They are also known to exhibit high levels of magnetic activity, with strong surface magnetic fields (~2–4 kG, compared with ~10 G on the Sun; Saar & Linsky Reference Saar and Linsky1985; Johns-Krull & Valenti Reference Johns-Krull and Valenti1996) and substantial filling factors (50%–80% of the surfaces of M dwarfs are covered by magnetic fields; Johns-Krull & Valenti Reference Johns-Krull and Valenti1996). Magnetic radio emission from M dwarfs has been observed in many nearby systems, both flaring and quiescent, predominantly in the 1–10-GHz band. These studies have confirmed the existence of large-scale, organised magnetic fields around stars with fully convective interiors (Donati et al. Reference Donati, Forveille, Cameron, Barnes, Delfosse, Jardine and Valenti2006), despite the loss of the αΩ dynamo that powers the Solar field (Parker Reference Parker1955).
For even lower mass stars and brown dwarfs, the detection of both quiescent and flaring radio emission was initially a surprise (Berger et al. Reference Berger2001), as the flux from these sources is orders of magnitude greater than that expected from the Güdel–Benz relation.Footnote 5 Several late-type sources have now been detected at GHz frequencies (Figure 8), in many cases despite the absence of optical or X-ray emission (see Berger Reference Berger2006 for a review). Indeed, while Hα and X-ray luminosities relative to bolometric luminosities appear to decline with spectral type, relative radio emission inexorably increases up to the substellar regime (see Burgasser & Putman Reference Burgasser and Putman2005; Berger Reference Berger2006; Audard et al. Reference Audard, Osten, Brown, Briggs, Güdel, Hodges-Kluck and Gizis2007). Understanding why radio emission is so prominent among these very low mass objects, and whether such emission correlates with age, rotation, or other physical parameters, remain outstanding questions.

Figure 8. Phase space for radio transients observable with the MWA at a nominal frequency of 200 MHz, updated and adapted from Cordes et al. (Reference Cordes, Lazio and McLaughlin2004). We plot the product of the observed peak flux density S peak and the square of the distance D 2 (like a luminosity) against the product of the emission frequency ν and the transient duration W. In the Rayleigh–Jeans approximation, these quantities are directly proportional and related to the brightness temperature T (given by the diagonal lines); we use a brightness temperature of 1012 K (thick diagonal line) to divide coherent and incoherent processes (Readhead Reference Readhead1994). The red lines show the predicted sensitivity of the MWA, assuming a 50-mJy source can be detected in 8 s. The vertical red lines give the timescales for individual snapshot observations (8 s), and short- and long-term surveys (5 m and 1 week). The red diagonal lines give the S peak D 2 limits corresponding to distances of 10 pc (appropriate for sources such as low-mass stars, brown dwarfs, and planets), 1 kpc (local Galactic sources), 10 kpc (the Galactic Center), 1 Mpc (local group), and 1 Gpc (extragalactic sources); the dotted lines show an estimated confusion limit of 10 mJy, although we can search below this limit using image subtraction or for polarised emission.
Radio flares in particular demonstrate that this emission is associated with magnetic events, occurring over timescales of microseconds to minutes (e.g. Osten & Bastian Reference Osten and Bastian2006). The brightness temperatures of bursting emissions frequently exceed 109 K, indicating coherent processes as confirmed by high circular polarisations (30%–100%). Yet, radio variability from these sources is remarkably diverse, from strong (30-mJy peak flux), narrowband, fully polarised, bursting emission with frequency drifts (Burgasser & Putman Reference Burgasser and Putman2005), to periodic bursts suggestive of pulsar-like beaming (Hallinan et al. Reference Hallinan2007, and Figure 8), to order-of-magnitude variations spanning years (Antonova et al. Reference Antonova, Doyle, Hallinan, Golden and Koen2007). It has even been suggested that the observed ‘quiescent’ emission from these sources may be the result of low-level, sustained electron cyclotron maser emission (e.g. Hallinan et al. Reference Hallinan2007). The physical origin of transient radio bursts from low-mass stars, their incidence rates (duty cycle estimates range from 1%–30%), and their spectral characteristics are either poorly constrained or entirely unknown. These questions have a direct impact on whether low-mass stars comprise a significant fraction of radio transients in general (e.g. Kulkarni & Phinney Reference Kulkarni and Phinney2005; Kaplan et al. Reference Kaplan, Hyman, Roy, Bandyopadhyay, Chakrabarty, Kassim, Lazio and Ray2008).
The MWA has the potential to contribute substantially to our understanding of both quiescent and flaring magnetic emission from low-mass stars and brown dwarfs. By sampling the 80–300-MHz band, MWA observations can be used to constrain the peak frequency (νpk) and spectral indices about νpk, enabling the determination of coronal field strengths (currently estimated at 10–100 G; Burgasser & Putman Reference Burgasser and Putman2005; Berger Reference Berger2006), electron densities and the fundamental nature of the emission. Audard et al. (Reference Audard, Osten, Brown, Briggs, Güdel, Hodges-Kluck and Gizis2007) argue that radio emission from very low mass stars may in fact peak in the ~100-MHz range if it arises from electron cyclotron emission from weak fields (νpk = νc = 30–300 MHz for 10–100-G fields; see also Osten et al. Reference Osten, Hawley, Bastian and Reid2006). The sensitivity of the MWA is essential for this work, given the intrinsic faintness, but variable nature, of radio emission from low-mass stars; estimates range over 10 μJy to 100 mJy at 100 MHz at a distance of 10 pc, depending on the emission mechanism. Similarly, the MWA's wide-field capabilities are necessary to build up statistically robust samples, particularly given the roughly uniform distribution of nearby low-mass stars in the vicinity of the Sun. High spectral resolution observations enabled by the MWA will permit studies of field dynamics and remote determinations of physical parameters such as the heights of magnetic reconnection regions, electron speeds, and the density profile of the stellar coronae.
4.1.2 Magnetars
While a variety of neutron stars can produce transient or steady radio emission (discussed in more detail in Section 4.4), some subclasses of neutron stars can give rise to extremely energetic, explosive phenomena. With magnetic fields of ~1015 G, magnetars (Duncan & Thompson Reference Duncan and Thompson1992; Thompson & Duncan Reference Thompson and Duncan1995) undergo catastrophic reconnection events known as ‘giant flares’ that release >1043 erg. With each flare the magnetars release blobs of relativistic plasma (Frail, Kulkarni, & Bloom Reference Frail, Kulkarni and Bloom1999; Gaensler et al. Reference Gaensler2005b; Cameron et al. Reference Cameron2005) with peak fluxes of hundreds of mJy at frequencies from 200 MHz up to 100 GHz (Figure 8). Such events are detected through high-energy satellites, but the radio monitoring provides vital diagnostics of the flare properties and energetics.
Beyond this, some magnetars unexpectedly have steady radio emission that is modulated at the X-ray pulse period (2–12 s). Prior searches for steady-state radio emission from magnetars had not been successful (e.g. Kaplan et al. Reference Kaplan, Kulkarni, Frail and van Kerkwijk2002), but Halpern et al. (Reference Halpern, Gotthelf, Becker, Helfand and White2005) found a radio source coincident with the magnetar XTE J1810–197 (also Camilo et al. Reference Camilo, Ransom, Halpern, Reynolds, Helfand, Zimmerman and Sarkissian2006, and others). Monitoring the magnetars through both individual pulses and phase-averaged emission, looking for both giant flares and the onset of bright phases, will help understand the duty cycles of the radio-bright phases and hence unravel the puzzles that they present.
4.1.3 X-ray binaries
Relativistic outflows or jets are a widespread yet transient consequence of accretion onto compact objects. Radio jets are seen for black-hole binaries (BHBs) and some neutron-star binaries (NSBs). These sources are collectively called ‘microquasars’ (Figure 8), since they exhibit scaled-down and rapidly evolving versions of the jets in active galactic nuclei. Microquasars exhibit several types of jets with different ranges of radio power and ejection timescale. Their study is crucially dependent on the correlated variations in radio and X-ray properties.
The most common type of jet in microquasars is the quasi-steady jets associated with the X-ray hard state (Fender, Belloni, & Gallo Reference Fender, Belloni and Gallo2004; McClintock & Remillard 2006) that can persist for months in some sources. Steady jets are estimated to be mildly relativistic (i.e. ~0.7c; see Fender Reference Fender, Lewin and van der Klis2006), but there is uncertainty about the baryonic content and hence the scale of the mass outflow and the fraction of accretion energy needed to power such jets.
Impulsive ejections are also produced by BHBs and some NSBs and the brightest of these are seen as bipolar radio jets that move with velocities as high as 0.98c (Mirabel & Rodríguez Reference Mirabel and Rodríguez1999). Impulsive jets are associated with X-ray state transitions (Fender et al. Reference Fender, Belloni and Gallo2004). In two BHBs, superluminal radio ejections, coinciding with major X-ray flares, led to the appearance of X-ray jets (more than one year later), that were imaged with Chandra as the jets impacted the local ISM (Tomsick et al. Reference Tomsick, Corbel, Fender, Miller, Orosz, Tzioumis, Wijnands and Kaaret2003; Corbel et al. Reference Corbel, Kaaret, Fender, Tzioumis, Tomsick and Orosz2005). Smaller and more frequent ejections in BHBs are seen as correlated X-ray and radio flares with ~10-min timescales and radio-band delays (Eikenberry et al. Reference Eikenberry, Matthews, Muno, Blanco, Morgan and Remillard2000; Wilms et al. Reference Wilms, Pottschmidt, Pooley, Markoff, Nowak, Kreykenbohm and Rothschild2007). The available X-ray data usually reveal recurrent and abrupt changes in flux and spectral components that associate the small jets with instability cycles in the inner accretion disc.
Study of the connection between discs and jets is fundamentally based on correlated X-ray and radio behaviour, as outlined above. During the last decade, the primary limitation for this enterprise has been the absence of dedicated radio instruments that can partner with X-ray facilities, but the MWA will radically change this landscape. Additional partners for jet investigations arise with Fermi (10 keV to 300 GeV) and the recent expansions of TeV observatories (e.g. HESS and VERITAS; 50 GeV to 50 TeV).
Recent measurements with the GMRT (150–1450 MHz) in India have shown variable radio emission in GRS 1915+105 (see Figure 8; Ishwara-Chandra et al. Reference Ishwara-Chandra, Rao, Pandey, Manchanda and Durouchoux2005) and Sco X–1 (Pandey et al. Reference Pandey, Rao, Manchanda, Durouchoux, Ishwara-Chandra and Kulkarni2005), with spectra that do not exhibit self-absorption cutoff at low frequencies. This is interpreted as emission from the outer regions of a compact jet and from an optically thin impulsive jet, respectively (also see Pandey et al. Reference Pandey, Rao, Pooley, Durouchoux, Manchanda and Ishwara-Chandra2006, Reference Pandey, Rao, Ishwara-Chandra, Durouchoux and Manchanda2007).
Overall, the MWA has the capability to monitor many known sources for which X-ray activity is detected, establishing outburst statistics and extending the spectra down to low frequencies where the total energetics are constrained. These observations can help to measure the burst luminosity function and the X-ray/radio correlation, and investigate their dependences on various intrinsic source parameters such as mass and X-ray luminosity. The MWA will provide data archives for the two microquasars that are reliable sources of jets: SS 433 and GRS 1915+105, as well as the BHBs and NSBs with the fastest outburst recurrence time (1–2 years: 4U 1630–47, and GX339–4, Aql X–1, 4U 1608–52, and the rapid burster). These monitoring observations will also find new outbursts of known sources, acting as a trigger for observations across the electromagnetic spectrum. Finally, the MWA has the potential to discover new sources: the large majority of the known BHBs and candidates are transient sources that were discovered because of their X-ray outbursts (Remillard & McClintock Reference Remillard and McClintock2006).
4.2 Serendipitous transient sources
Beyond the source categories discussed above, there are a number of object classes which we might hope to see (see Cordes et al. Reference Cordes, Lazio and McLaughlin2004; Fender et al. Reference Fender2006). These vary from the local to the cosmological, and the population predictions also span a wide range. Currently, low-frequency transient radio emission has been proposed but not observed for these objects, and there are only limited observational constraints. Such sources are among the most exciting possibilities for the MWA transient surveys (Section 4.3). Those surveys cover a large area of unexplored phase space—orders of magnitude in several different parameters—and provide a real opportunity to discover unique sources.
4.2.1 Extra-solar planets
In the Solar System, Jupiter is a strong source of low-frequency radio emission produced by cyclotron maser processes in its magnetosphere (Gurnett Reference Gurnett1974; Wu & Lee Reference Wu and Lee1979). Observations have established that many of the Jovian planets discovered around other stars (e.g. Marcy et al. Reference Marcy, Butler, Fischer, Vogt, Wright, Tinney and Jones2005) have magnetic fields (Shkolnik, Walker, & Bohlender Reference Shkolnik, Walker and Bohlender2003), although the field strengths are not known. By analogy, many of those planets should have similar emission. This would then be a novel way of directly detecting the planetary companions, something that has only been possible in a few special cases otherwise (Charbonneau et al. Reference Charbonneau, Brown, Noyes and Gilliland2002). This would allow an unprecedented probe of the planetary systems, such as estimating properties of the planetary magnetosphere, measuring its rotation rate, and observing the interaction between the star and planet (Lazio et al. Reference Lazio, Farrell, Dietrick, Greenlees, Hogan, Jones and Hennig2004). Grießmeier, Zarka, & Spreeuw (Reference Grießmeier, Zarka and Spreeuw2007) discuss theoretical expectations for radio emission from known extrasolar planets. Most of the sources are predicted to emit at the microJansky level between 10 and 200 MHz. A handful of planets are expected to emit at the mJy level in the MWA bandpass. Their results are heavily model dependent and MWA observations of the currently known exoplanet population will help constrain further models.
There have been a number of searches for emission from such planets (e.g. Farrell, Desch, & Zarka Reference Farrell, Desch and Zarka1999; Bastian, Dulk, & Leblanc Reference Bastian, Dulk and Leblanc2000; Zarka et al. Reference Zarka, Treumann, Ryabov and Ryabov2001; Lazio et al. Reference Lazio, Farrell, Dietrick, Greenlees, Hogan, Jones and Hennig2004; Lazio & Farrell Reference Lazio and Farrell2007). There are no detections to date, although the results are not very constraining. The emission is predicted to be very sporadic and bursty, and it is difficult to search effectively for such emission with pointed instruments like the VLA. Instead, new instruments like the MWA are likely to be the best way to detect extra-solar planets (Lazio et al. Reference Lazio, Farrell, Dietrick, Greenlees, Hogan, Jones and Hennig2004).
4.2.2 Explosive events
GRBs and radio supernovae may both produce short- and long-duration transient radio signals. The afterglow emission from each type will provide signals at the upper frequencies accessible to the MWA that are delayed from the initial explosion (due both to plasma in the ISM and to changing opacities) and slowly brighten over a few weeks to months (Morales et al. Reference Morales, Hewitt, Kasper, Lane, Bowman, Ray and Cappallo2005). These afterglows can be important diagnostics for explosion energetics (Soderberg et al. Reference Soderberg2007, Reference Soderberg2010) and can help understand particle acceleration in the nearby Universe (Chakraborti et al. Reference Chakraborti, Ray, Soderberg, Loeb and Chandra2011). While the long timescales of such events at low frequencies make the MWA unfavourable for their discovery, it will be able to study afterglows of events identified initially at higher frequencies.
GRBs, supernovae, and other explosions may also produce prompt pulses of coherent emission during the initial explosion (Colgate & Noerdlinger Reference Colgate and Noerdlinger1971; Nakar & Piran Reference Nakar and Piran2011). The theorised prompt signals are produced by coherent emission near the explosive shock. Proposed mechanisms include current oscillations (Usov & Katz Reference Usov and Katz2000), synchrotron maser activity behind the shock (Sagiv & Waxman Reference Sagiv and Waxman2002), or collective plasma modes as seen in solar bursts (Moortgat & Kuijpers Reference Moortgat, Kuijpers, Chen, Bloom, Madejski and Patrosian2005). Models by Hansen & Lyutikov (Reference Hansen and Lyutikov2001) and Benz & Paesold (Reference Benz and Paesold1998) also predict detectable emission, depending on the plasma environment and dynamics of the GRB. Some of these signals will be accompanied by bursts of radiation at other wavelengths, while some may offer the potential for multi-messenger astronomy by correlating radio and gravitational-wave signals (Nakar & Piran Reference Nakar and Piran2011; Palenzuela, Lehner, & Liebling Reference Palenzuela, Lehner and Liebling2010).
The detection of such prompt emission from GRBs offers a number of unique insights into the properties of the bursts, the intergalactic medium, and cosmology (Morales et al. Reference Morales, Hewitt, Kasper, Lane, Bowman, Ray and Cappallo2005). First, the details of the emission that we see depend heavily on the specific model for the shock structure, as discussed above. Second, we can use the emission as a probe of the media through which it propagates: we will see delays and dispersion from the local plasma, the host galaxy's ISM, the intergalactic medium (details of which can depend on cosmic reionisation), and the Milky Way's ISM (Inoue Reference Inoue2004).
Past searches for prompt radio emission from GRBs (Dessenne et al. Reference Dessenne1996; Benz & Paesold Reference Benz and Paesold1998; Balsano Reference Balsano1999) were all unsuccessful. Other projects attempted to perform blind surveys for radio transients (Amy, Large, & Vaughan Reference Amy, Large and Vaughan1989; Baird et al. Reference Baird, Meikle, Jelley, Palumbo and Partridge1976; Katz et al. Reference Katz, Hewitt, Corey and Moore2003). All of these attempts have suffered from constraints inherent in narrowband receivers and simple transient identification systems. More modern projects like GASE and ETA (Morales et al. Reference Morales, Hewitt, Kasper, Lane, Bowman, Ray and Cappallo2005; Patterson et al. Reference Patterson, Ellingson, Martin, Deshpande, Simonetti, Kavic and Cutchin2009) were designed to correct many of these problems, with digital baseband recording and interference rejection through de-dispersion, but the collecting areas are still very small.
4.2.3 New opportunities
Above we discussed two classes of sources that are expected to emit low-frequency radio transients, and where the detection of such transients would enable us to make significant advances in our understanding of such objects, but where we do not know the source properties enough to consider them ‘guaranteed’ science. Beyond even those classes are additional objects that may be found with blind searches (e.g. neutron star binary inspiral events that may produce radio precursors; Hansen & Lyutikov Reference Hansen and Lyutikov2001).
To date, systematic transient searches with radio telescopes have yielded some results, but they have largely been difficult to interpret (e.g. Matsumura et al. Reference Matsumura2007, Reference Matsumura2009), due to poor statistics, limited localisation, and a long time before follow-up. However, there have been successes that, while enigmatic, hint at the potential offered by the MWA. We do not give a full review here, but point to particular detections that hold promise for the MWA.
While searching for transient events at the Galactic Centre (GC), Hyman et al. (Reference Hyman, Lazio, Kassim and Bartleson2002) found two sources, one of which is an X-ray binary, but the other remains unclassified, although it varies on long timescales (~months). Later searches (Hyman et al. Reference Hyman, Lazio, Kassim, Ray, Markwardt and Yusef-Zadeh2005, also see Hyman et al. Reference Hyman, Wijnands, Lazio, Pal, Starling, Kassim and Ray2009) found a much more rapidly variable source, with flares on timescales of minutes that repeated (sometimes) every 77 min (GCRT J1745 in Figure 8). The positional coincidence with the GC, along with the greatly increasing source density near the Centre, suggests that it is at a distance of about 8 kpc, but this could be a selection effect because all the fields searched for transients in the programme were in that direction. Bower et al. (Reference Bower, Roberts, Yusef-Zadeh, Backer, Cotton, Goss, Lang and Lithwick2005) found another transient near the GC, but they deduced that it was an X-ray binary with a jet outburst interacting with the dense medium in that region.
For searches of high-latitude fields, Bower et al. (Reference Bower, Saul, Bloom, Bolatto, Filippenko, Foley and Perley2007) followed by Frail et al. (Reference Frail, Kulkarni, Ofek, Bower and Nakar2012) searched archival VLA data at cm wavelengths and identified at least one very faint (sub-mJy) transient source. Jaeger et al. (Reference Jaeger, Hyman, Kassim and Lazio2012) did repeated observations at a frequency of 325 MHz (closer to the MWA band) and did identify one significant transient of unknown origin, although they consider several possibilities including a distant flare star. Only recently have surveys moved beyond examinations of archival data (e.g. Bannister et al. Reference Bannister, Murphy, Gaensler, Hunstead and Chatterjee2011), with a wide range of flux limits and timescales, to systematic examinations of the variable sky (e.g. Lenc et al. Reference Lenc, Garrett, Wucknitz, Anderson and Tingay2008; Croft et al. Reference Croft, Bower, Keating, Law, Whysong, Williams and Wright2011). It is becoming clear that radio transients are rare but promising targets that will lead to advances in a number of areas of astrophysics.
4.3 Planned searches
We will conduct a continuous search for transient radio emission in each image produced by the MWA's real-time system, looking for changes from the previously observed sky on timescales ranging from 8 s to months (eventually using the high-quality integrated data from the sky surveys). This search will be more than six orders of magnitude more sensitive than previous transient surveys in the band and will cover a much broader range of frequencies, transient durations, and dispersion delays.
Eventually the full transient capabilities of the MWA will (1) cover 0.25 steradian instantaneously—approximately ~3% of the visible sky—with full polarisation coverage; (2) search blindly over that area orders of magnitude deeper than previous work; (3) simultaneously record light curves and spectra for hundreds of sources and conduct routine observation of tens of thousands of sources per week; (4) obtain typical exposures of days/source, with hundreds to thousands of hours for sources in selected areas (Galactic plane and EOR fields) over one year; and (5) record full electric field time series for a subset of observations.
New sources detected by the MWA will have relatively poor (approximately arcminute) localisation. This will hinder interpretation as many possible counterparts will be present at other wavelengths (e.g. Kaplan et al. Reference Kaplan, Hyman, Roy, Bandyopadhyay, Chakrabarty, Kassim, Lazio and Ray2008). Prompt multi-wavelength follow-up with wide-field imaging instruments will be crucial to help mitigate this, as the detection of contemporaneous variability at other wavelengths will significantly improve the localisation of sources and will pave the way for more detailed follow-up observations such as spectroscopy.
Source confusion will limit the sensitivity of the MWA for source detection. However, time variability is a classic way to help beat the confusion limit (i.e., searches for pulsars with single-dish telescopes). Subtracting images of the sky taken over successive time periods will help beat down the confusion noise and allow transients to emerge, especially when correlated with observations at other wavelengths. Finally, the examination of polarised images that have much lower background source levels will allow searches for bright and highly polarised transients like GCRT J1745–3009 (Hyman et al. Reference Hyman, Lazio, Kassim, Ray, Markwardt and Yusef-Zadeh2005).
4.4 Pulsars
With approximately 2 000 now known (Figure 9), pulsars offer opportunities to study a range of astrophysical phenomena, from the microscopic to the Galactic. The MWA's wide coverage in frequency and large collecting area makes it a unique instrument for low-frequency detection and detailed studies of pulsars and fast transients. The areas of pulsar science that the MWA would probe at low frequencies include pulsar phenomenology and pulsar searches, in general, and single-pulse and giant pulse studies, in particular. This is highlighted by the successful detection of giant pulses from the Crab Nebula pulsar at 200 MHz with only three prototype MWA antenna tiles (Bhat et al. Reference Bhat2007).

Figure 9. P–Ṗ diagram showing the distribution of the known pulsar population. The diamonds show the magnetars (SGRs and AXPs) and the stars the RRATs; binary systems are circled. The diagonal lines show loci of constant dipole magnetic field (solid) and spin-down age (dotted), while the dot–dashed line is an approximate ‘death-line’ for pulsar activity. The MWA will be uniquely sensitive to the slower, transient population while maintaining sensitivity to a considerable fraction of the millisecond pulsar population in the lower left.
The MWA will be able to observe at rates faster than the 0.5–8 s correlator integrations using a voltage capture system capable of recording, for several hours, correlator input data. This system will provide Nyquist sampled voltage streams for 3072 × 10 kHz channels comprising the full instantaneous bandwidth from each of the 128 antennas of the MWA that will enable high time-resolution studies of several types of objects, including pulsars and fast transients over the ~1 000 deg2 tile beam.
It is at MWA frequencies that pulsar emission peaks (Maron et al. Reference Maron, Kijak, Kramer and Wielebinski2000; Kondratiev et al. Reference Kondratiev and Stappers2012) and that interstellar propagation effects are easiest to study, but this wavelength range has been neglected for years because of difficulties in processing the data and the increasing prevalence of radio frequency interference (RFI). This has left the low-frequency pulsar population largely unconstrained. Since low frequencies select against distant objects (especially for fast pulsars), the MWA will provide important new constraints for the local, low-frequency population. As a baseline, in an 8-h pointing at 200 MHz we should have a 8σ sensitivity limit of 1.8 mJy for long-period pulsars. When corrected to 1 400 MHz using a spectral index of −1.8 (Maron et al. Reference Maron, Kijak, Kramer and Wielebinski2000), this would be 0.05 mJy, comparable to or better than ongoing surveys like the High Time Resolution Universe survey (Keith et al. Reference Keith2010) or the Green Bank 350-MHz Driftscan Survey (Boyles et al. Reference Boyles2013; Lynch et al. Reference Lynch2013).
Studies of individual pulsars help address a number of areas of astrophysics, providing unique insight into the as-yet poorly understood pulsar emission mechanism and astrophysical plasmas (Melrose Reference Melrose2003). Assembling an average pulse profile from thousands of individual pulses can help investigate the emission further, probing the emission altitude, beam geometry, and inclination of the magnetic field from the spin axis (Jenet, Anderson, & Prince Reference Jenet, Anderson and Prince2001; Gupta & Gangadhara Reference Gupta and Gangadhara2003; Kondratiev et al. Reference Kondratiev and Stappers2012; Hassall et al. Reference Hassall2012). Statistics derived from average pulse profiles may be among the best probes of complicated phenomena like core-collapse supernova (e.g. Johnston et al. Reference Johnston, Hobbs, Vigeland, Kramer, Weisberg and Lyne2005). Longer timescale variations in the emission can directly constrain the density of the magnetospheric plasma (Kramer et al. Reference Kramer, Lyne, O'Brien, Jordan and Lorimer2006).
Single-pulse studies should be possibleFootnote 6 for a sample of pulsars in excess of 100, with the full MWA system at frequencies >100 MHz (Kondratiev & the LOFAR Pulsar Working Group Reference Kondratiev and van Leeuwen2012). In cases of bright pulsars, we aim to probe the polar emission regions at different heights in greater details to study single-pulse fluctuations simultaneously across a wide range of radio frequencies, believed to come from different heights from the star surface. Mapping of the emission patterns corresponding to different heights simultaneously will enable tomography of the pulsar emission cone (Maan et al. Reference Maan2013; Asgekar & Deshpande Reference Asgekar and Deshpande2001; Deshpande & Rankin Reference Deshpande and Rankin1999). The wide bandwidth of MWA can probe a large fraction of the emission cone, and at larger distances from the star than higher frequency telescopes, revealing much needed clues about the mechanism of pulsar radio emission, which is still poorly understood even after 40 years of pulsar studies.
4.4.1 Rotating radio transients
While observations of pulsars with regular steady pulses reveal much about those sources, it is in sources where the pulsar emission becomes irregular that we can hope to gain disproportionate insight about the pulsar emission mechanism and the relation of pulsars to other more exotic classes of neutron stars. In particular, the rotating radio transients (RRATs; McLaughlin et al. Reference McLaughlin2006; Figure 9) likely serve as links to other more extreme populations. The RRATS emit only sporadic dispersed radio bursts of between 2 and 30 ms in duration that are separated by 4 min to 3 h, but nonetheless are identifiable as rotating neutron stars by their long-term spin-down. Initial estimates suggest that there could be as many RRATs as traditional pulsars (McLaughlin et al. Reference McLaughlin2006; Keane et al. Reference Keane, Ludovici, Eatough, Kramer, Lyne, McLaughlin and Stappers2010), but their properties do not appear the same, as they occupy different parts of the P–Ṗ diagram (see Figure 9).
The study of RRATs and sources with and without radio emission may help link the canonical rotation-powered pulsars—neutron stars that emit primarily in the radio and that are powered by rotational energy—to other classes of neutron stars that are powered via other energy sources. In particular, the X-ray and γ-ray sources known as magnetars (Woods & Thompson Reference Woods, Thompson, Lewin and van der Klis2006), which manifest observationally as the currentlyFootnote 7 11 confirmed anomalous X-ray pulsars (AXPs) and 9 soft gamma-ray repeaters (SGRs), are powered by the decay of superstrong (≳1014 G) magnetic fields. In contrast, the soft X-ray sources known as isolated neutron stars (INS; Kaplan Reference Kaplan, Yuan, Li and Lai2008) are powered by residual heat, but may be the decayed remnants of old magnetars (Kaplan & van Kerkwijk Reference Kaplan and van Kerkwijk2009). There is currently a great deal of interest in linking radio pulsars to these populations. At least two magnetars have been seen as transient radio pulsars (Camilo et al. Reference Camilo, Ransom, Halpern, Reynolds, Helfand, Zimmerman and Sarkissian2006, Reference Camilo, Ransom, Halpern and Reynolds2007), while radio searches for the INS have so far been negative (Johnston Reference Johnston2003; Kaplan, Kulkarni, & van Kerkwijk Reference Kaplan, Kulkarni and van Kerkwijk2003; Kondratiev et al. Reference Kondratiev, McLaughlin, Lorimer, Burgay, Possenti, Turolla, Popov and Zane2009). The populations may be linked via RRATs: the X-ray and timing characteristics of the RRATs offer tantalising clues to their relation to both magnetars (Lyne et al. Reference Lyne, McLaughlin, Keane, Kramer, Espinoza, Stappers, Palliyaguru and Miller2009) and the INS (Popov, Turolla, & Possenti Reference Popov, Turolla and Possenti2006; McLaughlin et al. Reference McLaughlin2007), but as yet nothing firm has been established (Keane & Kramer Reference Keane and Kramer2008).
The identification of RRATs relies on detecting single, dispersed pulses rather than steady repeating pulses (as in Keane et al. Reference Keane, Kramer, Lyne, Stappers and McLaughlin2011; Burke-Spolaor & Bailes Reference Burke-Spolaor and Bailes2010). They do appear as repeating transients and so many of the techniques required will be similar to those for other transients (Lorimer et al. Reference Lorimer, Bailes, McLaughlin, Narkevic and Crawford2007; Keane et al. Reference Keane, Stappers, Kramer and Lyne2012). We will also explore the bispectrum techniques of Law & Bower (Reference Law and Bower2012), which enable computationally simple searches for dispersed pulses at the expense of S/N, although the small area of each antenna leads to a low S/N on each baseline, making such searches (Law et al. Reference Law, Bower, Pokorny, Rupen and Sowinski2012) significantly less sensitive than traditional beamforming.
4.4.2 Interstellar medium
Beyond the study of pulsars themselves, variations in individual pulses with time and frequency can be used to probe the properties of the ISM (Hassall et al. Reference Hassall2012) and the Galactic magnetic field (Noutsos et al. Reference Noutsos, Johnston, Kramer and Karastergiou2008), as well as the solar corona (Ord, Johnston, & Sarkissian Reference Ord, Johnston and Sarkissian2007). Signals of short intrinsic duration do not survive passage through interplanetary, interstellar, or intergalactic plasma unscathed (Rickett Reference Rickett1990; Cordes et al. Reference Cordes, Weisberg, Frail, Spangler and Ryan1991; Taylor & Cordes Reference Taylor and Cordes1993) and are distorted via dispersion (Cordes & Lazio Reference Cordes and Lazio2002), scintillation (Rickett Reference Rickett1969), scattering (Bhat et al. Reference Bhat, Cordes, Camilo, Nice and Lorimer2004), and FR.
Dispersion makes lower frequencies arrive later. Compared with a signal at infinite frequency, a signal of frequency ν arrives with a time delay ∝ν−2. Dispersive delay can be both an advantage and a disadvantage. A radio counterpart to a transient event, such as a GRB, observed with a high-energy satellite, would be delayed by several minutes to hours before it arrives in the MWA band. This delay is beneficial since it allows time to prepare for the event at low frequencies (e.g. Cordes & McLaughlin Reference Cordes and McLaughlin2003; Macquart Reference Macquart2007). But the converse is also true. If the MWA provides the first detection of a transient signal, it may be too late for other facilities at higher frequencies to observe it.
Scattering is the result of multi-path propagation in ionised media. While it has other effects, such as spectral and angular broadening, we are primarily concerned with temporal broadening here. This leads to information on timescales shorter than the scattering time being lost, and this time scales as ∝ν−22/5. Because of this steep scaling, this tends to set a minimum useful timescale for low-frequency observations. The scattering timescale becomes comparable to the standard MWA correlator integration time of 0.5 s in the Galactic plane for objects beyond ~5 kpc (Cordes & Lazio Reference Cordes and Lazio2002). Hence, the MWA will be most sensitive to scattering effects for sources within this distance.
5 SOLAR, HELIOSPHERIC, AND IONOSPHERIC SCIENCE
The MWA will make significant contributions to the fields of solar, heliospheric, and ionospheric science through a diverse set of novel radio measurements, as described here and in earlier papers (Bastian Reference Bastian2004; Cairns Reference Cairns2004; Oberoi & Kasper Reference Oberoi and Kasper2004; Salah et al. Reference Salah, Lonsdale, Oberoi, Cappallo and Kasper2005; Oberoi & Benkevitch Reference Oberoi and Benkevitch2010). These measurements directly address space weather, defined as the study of the impact of the Sun on the Earth and its neighbourhood. Space weather effects are mostly driven by solar flares and coronal mass ejections (CMEs) that produce electromagnetic radiation (from X-rays to radio wavelengths), energetic particles, shock waves, changes in magnetic fields, and fast-moving plasma outflows that couple to the magnetosphere, ionosphere, neutral atmosphere, and surface of the Earth. These responses can directly affect humanity's environment, technology, and society (Scherer et al. Reference Scherer, Fichtner, Heber, Mall, Scherer, Fichtner, Heber and Mall2005; Warmuth & Mann Reference Warmuth and Mann2004). The MWA will be able to observe and track CMEs, shocks, and other plasma structures from points close to their inception through their journey to the Earth and beyond, and it will be able to characterise their impact on the terrestrial ionosphere, making it a powerful instrument for space weather studies.
5.1 Solar science
Even the quiet radio Sun is a time-variable, spectrally and morphologically complex, extended source. Emission features are especially remarkable during periods of high solar activity. The active Sun produces both broadband (Δf/f ≈ 1) and narrowband (Δf/f ≪ 10−2) emissions at frequencies from below 1 MHz to approximately 30 GHz (e.g. Wild, Smerd, & Weiss Reference Wild, Smerd and Weiss1963; Bastian, Benz, & Gary Reference Bastian, Benz and Gary1998; Cane, Erickson, & Prestage Reference Cane, Erickson and Prestage2002; Karlický Reference Karlický2003; Cairns 2011). Variations in the emission can occur over timescales ranging from less than 1 ms to the 11-year cycle of solar activity. The complexity of solar radio emission presents a challenging radio imaging problem, but the unprecedented instantaneous dynamic range, wide bandwidth, high spectral resolution, and full-Stokes capability of the MWA will enable spectroscopic imaging of the dynamic Sun.
The physical sources of solar radio emission in the MWA band fall into three distinct categories: (1) thermal emission produced by hot electrons in all layers of the solar atmosphere, but especially the solar corona (McLean & Labrum Reference McLean and Labrum1985); (2) gyro-synchrotron and synchrotron emission with broad power-law spectra in frequency, created by electrons accelerated in magnetic loops and by shocks driven by CMEs (Bastian et al. Reference Bastian, Pick, Kerdraon, Maia and Vourlidas2001); and (3) intense bursts of nearly coherent narrowband emissions that are produced as the so-called type I, II, III, IV, and V bursts (e.g. Wild et al. Reference Wild, Smerd and Weiss1963; McLean & Labrum Reference McLean and Labrum1985; Cane et al. Reference Cane, Erickson and Prestage2002; Cairns Reference Cairns, Miralles and Almeida2011). The presence of multiple different emission mechanisms, along with propagation effects like refraction and scattering, endows radio observations with a rich and unique coronal diagnostics capability.
5.1.1 Electron density and temperature
Large gradients in electron density and temperature from the solar chromosphere to the coronal regions have the consequence that the optical depth to radio waves tends to be a sensitive function of the ray path, which itself is determined by the refraction due to the density gradients. The optical depth of ray paths at different frequencies is dominated by contributions from different coronal heights. Spectral imaging by the MWA, therefore, should make it possible to construct a three-dimensional distribution of electron density and temperature in the lower corona for the quiescent Sun.
5.1.2 Electron acceleration and radio bursts
Solar radio bursts are one of the primary remote signatures of electron acceleration in the corona and inner heliosphere. A wealth of information about bursts has been amassed, primarily from studies of their emission in frequency–time dynamic spectra. Their imaging studies remain rare. The standard models for these bursts involve the generation of radiation near the electron plasma frequency, νpe, as well as near 2νpe, where
We will focus on type II and III bursts with the MWA. Type II bursts are associated with suprathermal electrons accelerated at magnetohydrodynamic shocks to speeds of 400–2000 km s−1, whereas type III bursts are due to bursts of electrons moving at speeds of the order of one-third of the speed of light, produced in magnetic reconnection sites during solar flares (Wild et al. Reference Wild, Smerd and Weiss1963; Melrose Reference Melrose1980; Nelson & Melrose Reference Nelson, Melrose, McLean and Labrum1985; Bastian et al. Reference Bastian, Benz and Gary1998; Robinson & Cairns Reference Robinson, Cairns, Stone, Weiler, Goldstein and Bougerot2000; Cairns Reference Cairns, Miralles and Almeida2011).
Several major unresolved questions exist. The first is whether type II bursts are associated with a blast wave (i.e. a freely propagating shock) or the bow wave found upstream of a CME that is expanding into the heliosphere (Cane & Erickson Reference Cane and Erickson2005; Vršnak & Cliver Reference Vršnak and Cliver2008; Cairns Reference Cairns, Miralles and Almeida2011). The second problem is that estimates of density profiles that are derived by applying the plasma frequency relation to time-dependent spectra (Cairns et al. Reference Cairns, Lobzin, Warmuth, Li, Robinson and Mann2009; Lobzin et al. Reference Lobzin, Cairns, Robinson, Warmuth, Mann, Gorgutsa and Fomichev2010) have tended to be much shallower than expected, as shown in Figure 10. The density profile is coupled to the formation mechanism of the corona; hence, discrepancy with models casts doubt on the source of energetic electrons. Lastly, unresolved theoretical issues exist due to the relatively small levels of circular polarisation observed in type II and III bursts, despite existing theories predicting essentially 100% circular polarisation in the sense of the o mode (left hand) (Nelson & Melrose Reference Nelson, Melrose, McLean and Labrum1985; Suzuki & Dulk Reference Suzuki, Dulk, McLean and Labrum1985; Cairns Reference Cairns, Miralles and Almeida2011).

Figure 10. (a) Dynamic spectrum of the type III burst of 09:26 UTC on 1999 October 20, observed by the Potsdam-Tremsdorf Radiospectrograph, with normalised intensity (colour coded) as a function of frequency and time (Cairns et al. Reference Cairns, Lobzin, Warmuth, Li, Robinson and Mann2009). Horizontal bands are due to RFI. (b) Red diamonds show the (f, t) locations of flux maxima for each time. The green line is the best fit to ν(t) = a(t − b)−β/2 and implies that n e(r)~(r−1.0R S)−β with β = 2.0 ± 0.3. This unexpected result is a solar wind-like profile for n e(r). Fits for the leading power-law term β = 6 of the standard density model based on coronagraph data (blue line) and an exponential gravitational-settling profile (black line) agree poorly with the type III data.
The rapid spectroscopic imaging capability of MWA will address these issues by localising burst emission. An initial example of this capability is shown in Figure 11, in which the MWA development system imaged a solar burst at 15-arcmin angular resolution (Oberoi et al. Reference Oberoi2011). The 2-arcmin angular resolution of the full MWA will be nearly an order of magnitude better. This will help to determine the shock mechanism by providing radio positions to compare with CME observations (e.g. from STEREO), and it will improve density profile estimates by eliminating the need to infer burst location based on plasma frequency. In combination with the recent detailed models for the source regions and dynamics spectra of type II burst emission, as reviewed by Cairns (Reference Cairns, Miralles and Almeida2011), the MWA images and dynamic spectra should help to determine definitively the relationship between type II bursts, CMEs, and shocks and to provide strong tests of our understanding of the propagation of events between the source and Earth.
Figure 11. The top panels show a set of radio images at 193.3 MHz from the MWA development system on the same intensity scale (Oberoi et al. Reference Oberoi2011). From left to right, the first one comes from a time close to the peak of a weak non-thermal emission feature lasting ~10 s and occupying the entire ~30 MHz of observing bandwidth, the second is during one of numerous weaker events that spanned ~5 s and ~5 MHz, and the last one shows an image of steady solar emission for the nearly quiescent Sun, although with an active region still visible in the northern hemisphere. The dynamic range of these images is ~2 500 and exceeds that of earlier images by about an order of magnitude. The bottom panels show spatially localised spectra of emission across the solar disc at the same times as the top panels. The spectra are shown for every third pixel, the pixel size is 100 × 100 arcsec2. The spectra span the entire observing bandwidth, binned into 24 frequency bands spaced 1.28 MHz apart and averaged over 0.8 MHz. The y-axis ranges in arbitrary units are (left to right) 50–4 620, 100–6 000 and 100–1 800. Celestial north is on top, and the red circles mark the size of the optical solar disc.
5.1.3 Direct imaging of emission from CME plasma
Though CMEs are routinely imaged in visible light using coronagraphs, and CME-driven shocks produce broadband radio emissions over several hundred MHz to as narrow as 20 kHz, the CME plasma itself has been difficult to observe directly. Metre and decimetre frequencies are regarded as the most suitable in which to try to image the synchrotron, gyrosynchrotron, and/or thermal bremsstrahlung emission from the CME plasma (Bastian & Gary Reference Bastian and Gary1997). Such measurements offer very useful and unique diagnostic capabilities, including the ability to constrain the CME magnetic field remotely. To date, however, only a few events have been confidently interpreted this way (e.g. Bastian et al. Reference Bastian, Pick, Kerdraon, Maia and Vourlidas2001; Maia et al. Reference Maia, Pick, Vourlidas and Howard2000). Observing these events is particularly challenging for existing instruments due to the large contrasts between the inherent brightness of the non-thermal emission from the CME plasma (weak) and solar disc (strong), and other phenomenon which are often simultaneously present (e.g. noise storms), and the large angular scales of this relatively weak emission. With its significantly higher dynamic range imaging ability and higher sensitivity to extended emission scales, owing to its numerous short baselines, the MWA should be the most suitable instrument yet for direct imaging of emissions from the CME plasma.
5.2 Heliospheric science
With an increasing reliance on the robust functioning of satellites, humankind is now more affected by space weather than ever before. Reliable predictions of space weather are needed to protect our technological assets in orbit as well as humans in space. The largest of the space weather events are caused by CMEs, and the geo-effectiveness of CMEs is closely tied to the presence of a southward-directed magnetic field in the CME or behind the CME-driven shock. Currently, the only operational means of obtaining this information is from the in situ observations by the near-Earth satellites. This approach suffers from two significant disadvantages: (1) These measurements provide a lead time of only a few hours; consequently, the advance warning comes so close to the event itself that it leaves little opportunity to take any remedial measures. (2) At these crucial times, interactions between the CME's magnetic field and plasma significantly alter the coupling between Earth's ionosphere and magnetosphere and the solar wind, leading to major changes in energetic particle flux, plasma density, plasma motion, magnetic and electric fields, and ionospheric activity. Degradation in satellite hardware and communication performance then occur, as well as many other space weather effects.
5.2.1 Faraday rotation
The observation of FR of background polarised radio sources (see also Section 3.3) is the only known remote sensing technique sensitive to the orientation and magnitude of the interplanetary magnetic field. Changes in FR associated with the passage of the solar corona or CMEs through the line of sight to spacecraft were convincingly detected using the telemetry signal from the Pioneer 6 and Helios satellites (Stelzried et al. Reference Stelzried, Levy, Sato, Rusch, Ohlson, Schatten and Wilcox1970; Bird Reference Bird1982; Bird et al. Reference Bird1985). More recently, coronal FR has been detected using VLA observations of radio galaxies as the Sun passes in front of them (Mancuso & Spangler Reference Mancuso and Spangler2000; Spangler & Whiting Reference Spangler and Whiting2009). The ability to routinely monitor and track CME magnetic fields would revolutionise the field of space weather.
FR measurements have been applied to many interesting studies of the nature of the solar corona and the solar wind, including to determine the mean magnetic field in the corona (Patzold et al. Reference Patzold, Bird, Volland, Levy, Seidel and Stelzried1987), to measure the power spectrum of coronal waves and turbulence as a function of distance (Efimov et al. Reference Efimov, Bird, Andreev and Samoznaev1996), to suggest the existence of intermittent waves at single locations (Chashei et al. Reference Chashei, Bird, Efimov, Andreev and Samoznaev1999), to support theoretical models of wave dissipation as a coronal heating mechanism (Hollweg et al. Reference Hollweg, Bird, Volland, Edenhofer, Stelzried and Seidel1982), and to study the structure of the heliospheric current sheet (Mancuso & Spangler Reference Mancuso and Spangler2000).
Studies so far have been severely limited by the paucity of suitable linearly polarised sources and the narrow fields of view of existing instrumentation (Spangler & Whiting Reference Spangler and Whiting2009). As discussed in Section 3.3, observations using the WSRT at 340–370 MHz have lead to detection of polarised extragalactic sources exhibiting typical polarised intensities of 20 mJy and readily measurable RMs (Wieringa et al. Reference Wieringa, de Bruyn, Jansen, Brouw and Katgert1993; Haverkorn, Katgert, & de Bruyn Reference Haverkorn, Katgert and de Bruyn2003a, Reference Haverkorn, Katgert and de Bruyn2003b, Reference Haverkorn, Katgert and de Bruyn2003c). In the few areas of the sky investigated in detail, these efforts reveal about one suitable polarised source every ~4 deg2, as well as patches of diffuse polarised emission (Bernardi et al. Reference Bernardi2013), suggesting that there will be sufficiently numerous background sources to chart CMEs.
The combination of the sensitivity of the MWA, its low frequency of operation, and its wide field of view, along with the availability of a large number of polarised sources with sufficient flux density, present the possibility of being able to measure the coronal and heliospheric FR simultaneously to several different lines of sight and out to much larger distances from the Sun (~50 solar radii) than previously accessible. No measurements of FR due to CME plasma are available yet at large solar offsets; hence, we rely on simulations to build quantitative expectations. Jensen et al. (Reference Jensen, Hick, Bisi, Jackson, Clover and Mulligan2010) estimate the RM from CMEs to be ~0.05 rad m−2 (12° at 150 MHz) at about 0.4 AU. Liu et al. (Reference Liu, Manchester, Kasper, Richardson and Belcher2007) also arrive at a similar estimate and also show that the FR time series from instruments like the MWA during the CME passage may be used to infer the helicity and size of the CME.
For multiple reasons, these are rather challenging measurements to make (Oberoi & Lonsdale Reference Oberoi and Lonsdale2013). Ionospheric RM, is 1–10 rad m−2, more than an order of magnitude larger than the expected heliospheric or CME RM signature. This implies that we will need to achieve ionospheric RM calibration accuracies of a few per cent over large fields of view in order to study heliospheric RM. The quiet solar flux density is 104–105 Jy; hence, detecting 20 mJy sources requires polarimetric imaging dynamic range of about 106, in the vicinity of a strong and variable Sun.
5.2.2 Interplanetary scintillation
As radio waves from a distant compact radio source propagate through the turbulent and inhomogeneous solar wind plasma, the incident plane wavefronts pick up phase corrugations corresponding to density inhomogeneities. These phase corrugations develop into intensity fluctuations by the time the wavefronts arrive at the Earth-based telescope. Due to the motion of the solar wind, the interference pattern produced by these intensity fluctuations is swept past the telescope giving rise to observed scintillations.
The evolution and dynamics of solar wind in the inner heliosphere dominates space weather effects. However, there are few techniques available to study the solar wind in this vast region. Historically, interplanetary scintillation (IPS) was the first remote sensing technique used to investigate the solar wind in this region (Hewish, Scott, & Wills Reference Hewish, Scott and Wills1964). More recently, the routine availability of observations from heliospheric imagers (e.g. STEREO) that image very large parts of the heliosphere using white light scattered from the solar wind electrons, have emerged as very useful tools for investigations in the inner heliosphere. These techniques, along with local in situ sampling provided by most satellite-based instrumentation, complement each other well since they cover different spatial scales and have led to a more complete characterisation of the solar wind than would have been possible with either of the data sets (e.g. Jackson et al. Reference Jackson, Hick, Buffington, Bisi, Kojima and Tokumaru2007; Dorrian et al. Reference Dorrian, Breen, Brown, Davies, Fallows and Rouillard2008).
Several new instruments are coming online to study IPS. Apart from the MWA, the new facilities include the LOFAR (Bisi et al. Reference Bisi, Fallows, Jensen, Breen, Xiong and Jackson2011; Fallows et al. Reference Fallows, Asgekar, Bisi, Breen and ter-Veen2012) and the Mexico Array Telescope (Mejia-Ambriz et al. Reference Mejia-Ambriz, Villanueva-Hernandez, Gonzalez-Esparza, Aguilar-Rodriguez and Jeyakumar2010). In addition, the Ooty Radio Telescope in India (P. K. Manoharan, private communication, 2012) and Solar Wind Imaging Facility (SWIFT) in Japan (Tokumaru et al. Reference Tokumaru, Kojima, Fujiki, Maruyama, Maruyama, Ito and Iju2011) are both undergoing considerable upgrades which will substantially improve their scientific capabilities.
For the MWA, the primary IPS observable will be the power spectrum of observed intensity fluctuations, although we will also employ a less commonly used observable, the normalised co-spectrum obtained from simultaneous observations at frequencies differing by a factor of ~2 (Scott, Rickett, & Armstrong Reference Scott, Rickett and Armstrong1983; Zhang Reference Zhang2007). Under the assumption of weak scattering, the interplanetary medium can be regarded as a collection of thin screens placed along the line of sight, and the IPS observable can be modelled as a weighted sum of the contributions from each of the thin screens. The physical parameters to which IPS is sensitive are (1) the velocity of the solar wind; (2) the level of electron density fluctuations, δn e; (3) the spectral index of the δn e power spectrum; (4) the inner scale for the power law governing δn e; and (5) the axial ratio of δn e.
Using an inversion process, it is possible to extract the global three-dimensional distribution of IPM parameters (Jackson et al. Reference Jackson, Hick, Kojima and Yokobe1998; Kojima et al. Reference Kojima, Tokumaru, Watanabe, Yokobe, Asai, Jackson and Hick1998; Asai et al. Reference Asai, Kojima, Tokumaru, Yokobe, Jackson, Hick and Manoharan1998; Oberoi Reference Oberoi2000; Bisi et al. Reference Bisi, Jackson, Hick, Buffington, Odstrcil and Clover2008, Reference Bisi, Jackson, Breen, Dorrian, Fallows, Clover and Hick2010; Dorrian et al. Reference Dorrian2010; Xiong et al. Reference Xiong, Breen, Bisi, Owens, Fallows, Dorrian, Davies and Thomasson2011). The most important bottleneck currently constraining the fidelity and resolution of the inversion of IPS data, and hence its science output, are the sparseness (both in space and time) and the non-uniformity of the sampling of the heliosphere afforded by the present generation instrumentation (Oberoi & Benkevitch Reference Oberoi and Benkevitch2010). The MWA will represent a significant advance in addressing the bottleneck of limited heliospheric sampling when its voltage capture system is completed. The MWA will have a sensitivity of ~70 mJy (1 s and 30.72 MHz), comparable to that of the SWIFT transit facility currently under commissioning in Japan. The MWA will boost the number of independent IPS measurements by up to a factor of ~30 over what is possible with most present-day systems. The southern hemisphere location of the MWA also complements the heliospheric coverage provided by the existing facilities, all of which happen to be in the northern hemisphere. Combining these data with other MWA observations like solar imaging and FR observations, and the observations from other sources such as STEREO, SDO, and HINODE, will provide a very comprehensive data set for characterising the inner heliosphere, monitoring and tracking CME evolution from close to the Sun to our terrestrial neighbourhood. Furthermore, the software framework being developed for handling the MWA IPS data could provide a common data repository, interface, and analysis tools for IPS data from observatories across the world (Oberoi & Benkevitch Reference Oberoi and Benkevitch2010).
5.3 Ionospheric science
Propagation through the dynamic and structured magnetoionic ionospheric plasma leaves an imprint on the incident low radio frequency radiation from astronomical sources. In order to arrive at the true properties of the incident radiation, the ionospheric distortion must be identified and removed. The MWA can tackle this long-standing challenge by measuring the refractive shift in the apparent position of dozens of bright and relatively compact sources at a cadence of 8 s. The ionospheric calibration information thus comprises of a time series of vectors showing the refractive shift of calibrator sources from their fiducial positions. To first order, the magnitude of the shift is directly proportional to the ionospheric gradient in the total electron content (TEC) towards the fiducial sky position of the calibrator source. This information for all the observed calibrator sources leads to a series of differential TEC maps and an accuracy of ~0.01 TECU (1 TECU = 1016 electrons m−2). These maps, produced routinely as a part of the MWA calibration, will form the primary data products for ionospheric science. The MWA beam will sample a region about 175 km × 175 km at a height of ~300 km and the expected calibrator source density corresponds to spatial scales of ~10 km at this ionospheric height.
The high-precision and dense sampling of the ionosphere provided by the MWA offers new opportunities for ionospheric science. The three areas of ionospheric research that the MWA will make significant contributions are in (1) the measuring of waves in TEC associated with travelling ionospheric disturbances (TIDs); (2) the development of storm enhanced density (SED) and sharp TEC gradients associated with space weather events; and (3) the tracking of the onset and evolution of scintillation associated with the development of ionospheric irregularities.
5.3.1 Travelling ionospheric disturbances
TIDs are manifestations of middle-scale ionospheric irregularities arising as response to acoustic gravity waves. TIDs are frequently observed at high and middle latitudes (Bristow, Greenwald, & Villain Reference Bristow, Greenwald and Villain1996; Nicolls & Heinselman Reference Nicolls and Heinselman2007; Oliver et al. Reference Oliver, Fukao, Yamamoto, Takami, Yamanaka, Yamamoto, Nakamura and Tsuda1994, Reference Oliver, Otsuka, Sato, Takami and Fukao1997; Djuth et al. Reference Djuth, Sulzer, Gonzáles, Mathews, Elder and Walterscheid2004), and their activity and amplitudes vary depending on latitude, longitude, local time, season, and solar cycle (e.g. Kotake et al. Reference Kotake, Otsuka, Tsugawa, Ogawa and Saito2006; Hernández-Pajares, Juan, & Sanz Reference Hernández-Pajares, Juan and Sanz2006). They can be generated by auroral sources at the high latitude thermosphere, the passage of the solar terminator (Galushko et al. Reference Galushko, Beley, Koloskov, Yampolski, Paznukhov, Reinisch, Foster and Erickson2003), and storms, hurricanes, and tornados in the troposphere. Detailed information about the sources, energetics, and scale sizes of energy coupling from the lower atmosphere to the upper atmosphere, along with resulting ionospheric effects, is critical to developing a deep understanding of overall upper atmospheric energy balance. Measurements of TIDs at the VLA have been made since the early 1990s (Jacobson & Erickson Reference Jacobson and Erickson1993; Jacobson et al. Reference Jacobson, Carlos, Massey and Wu1995) and recent observations have been reported by Helmboldt et al. (Reference Helmboldt, Lazio, Intema and Dymond2012) and Helmboldt, Lane, & Cotton (2012). The fine grid over which the MWA calibration solutions will provide differential TEC measurements will provide detailed measurements of the propagation of TIDs over the array and TEC gradients or irregularities.
5.3.2 Storm enhanced density
The MWA is well sited to contribute to coordinate international investigations of the SED phenomenon (Foster Reference Foster1993). This process is responsible for some of the largest space weather effects at mid-latitudes (Coster & Foster Reference Coster and Foster2007) since it produces severe, temporally dependent electron density gradients. These gradients will be obvious in the differential TEC measurements made by the MWA. The geographic/geomagnetic pole offset in the southern hemisphere is anticipated to influence the development of SED near the MWA (Coster et al. Reference Coster, Colerico, Foster, Rideout and Rich2007; Foster & Coster Reference Foster and Coster2007; Foster & Erickson Reference Foster and Erickson2013). SED associated gradients have a practical consequence, as they cause large errors in GPS range measurements, and significantly degrade the high-precision positioning information provided by GPS systems. The MWA's longitude (~116° E) is very close to the longitude being extensively instrumented in the Asian sector as part of the Chinese Meridian project (~113°), and the conjugate longitude of ~64° W is within the field of view of the US-sponsored chain of incoherent scatter radars, in particular Millstone Hill. The combination of simultaneous measurements from these distributed sensors thus provides a unique way to determine mesoscale response to geomagnetic disturbances in the coupled geospace system. In particular, it will be possible to investigate whether there is a seasonal and universal time dependence of geomagnetic storm response by comparing American and Asian/Australian sector response to solar wind and CME forcing. Such effects have been predicted theoretically (Foster & Erickson Reference Foster and Erickson2013) but have not yet been confirmed by observations.
5.3.3 Ionospheric scintillation
Ionospheric scintillation can be defined as the rapid fluctuation of radio-frequency signal phase and/or amplitude, generated as a signal passes through the ionosphere. MWA observations using voltage capture capabilities will be uniquely suited for the exploration of ionospheric irregularities and scintillation. The voltage capture system should provide the ability to create array beams in post-processing that use the entire bandwidth and collecting area of the MWA, and that can be pointed independently anywhere within the MWA field of view. Such a system will provide scintillation measurements at multiple positions across the visible ionospheric region.
MWA array-beam observations will be augmented by data from specially designed GPS receivers at and near the MWA site that can measure L-band scintillation statistics. GPS TEC data from these receivers, when combined with data from a large number of newly deployed GPS receivers on the Australian continent, will provide important contextual information about the regional distribution of TEC around the MWA site. Other satellite-based remote-sensing platforms, including COSMIC, DMSP, and JASON, will also be available during overflights to provide further information about background ionospheric plasma and electrodynamic conditions in the ionosphere. A similar approach has been followed previously in the Combined Radio Interferometry and COSMIC Experiment in Tomography (CRICKET) campaign utilising the VLA (Dymond et al. Reference Dymond2008; Coker et al. Reference Coker, Thonnard, Dymond, Lazio, Makela and Loughmiller2009). This mix of data types allows for ionospheric specification from the global scale down to the regional scale.
6 CONCLUSION
The MWA is a unique low-frequency instrument with high survey efficiency and arcminute angular resolution. It will provide deep integrations on EoR target regions that could enable the first detection of the redshifted 21-cm signal and detailed characterisation of diffuse Galactic emission and faint extragalactic source populations. The planned full-Stokes southern hemisphere sky survey will include the Galactic Centre, Galactic plane, and the Large and Small Magellanic Clouds, making the MWA particularly well suited to identifying the missing population of SNRs, and thereby constraining the total energy budget of the Galaxy.
Long integrations in the EoR fields and regular observations along the Galactic plane will enable sensitive searches for pulsars and transient events on timescales from seconds to days. Blind surveys for both rare and faint events are planned, as well as targeted observations of known transient sources, including X-ray binaries, neutron stars, pulsars, and low-mass stellar objects.
The MWA will open new windows into space weather and solar physics and provide new measurements of solar bursts throughout their journey from the surface of the Sun to the Earth and on to the outer Solar System. High-dynamic range spectroscopic imaging will show the origin of bursts in the solar corona, while monitoring of interplanetary scintillation will probe the interstellar wind. At Earth, the MWA's calibration system will yield detailed measurements of ionospheric disturbances travelling over the telescope.
The telescope is complementary to other new low-frequency radio telescopes, falling between LOFAR and PAPER in both sensitivity and angular resolution. It is the only low-frequency SKA precursor and is located on the very radio-quiet site planned for the SKA low-band telescope. The combination of ASKAP and MWA at the MRO will yield a comprehensive programme of precursor science for the SKA over the coming years. The MWA possesses a versatile design with excess infrastructure capability that will allow the telescope and its users to embrace new scientific and technological opportunities over the coming decade, hopefully providing an enduring and fruitful future for the instrument.
ACKNOWLEDGMENTS
This scientific work makes use of the Murchison Radio-astronomy Observatory. We acknowledge the Wajarri Yamatji people as the traditional owners of the Observatory site. Support for the MWA comes from the U.S. National Science Foundation (grants AST-0457585, PHY-0835713, CAREER-0847753, and AST-0908884), the Australian Research Council (LIEF grants LE0775621 and LE0882938), the U.S. Air Force Office of Scientific Research (grant FA9550-0510247), and the Centre for All-sky Astrophysics (an Australian Research Council Centre of Excellence funded by grant CE110001020). Support is also provided by the Smithsonian Astrophysical Observatory, the MIT School of Science, the Raman Research Institute, the Australian National University, and the Victoria University of Wellington (via grant MED-E1799 from the New Zealand Ministry of Economic Development and an IBM Shared University Research Grant). The Australian Federal government provides additional support via the National Collaborative Research Infrastructure Strategy, Education Investment Fund, and the Australia India Strategic Research Fund, and Astronomy Australia Limited, under contract to Curtin University. We acknowledge the iVEC Petabyte Data Store, the Initiative in Innovative Computing and the CUDA Center for Excellence sponsored by NVIDIA at Harvard University, and the International Centre for Radio Astronomy Research (ICRAR), a Joint Venture of Curtin University and The University of Western Australia, funded by the Western Australian State government.















