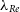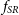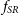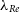1. Introduction
Our understanding of the formation and evolution of galaxies steadily progresses as our ability to probe galaxies advances. Stellar kinematics provide unique insight into a galaxy’s history and future, particularly when studied in conjunction with other galaxy properties such as environment, mass, and age. The rise of integral-field spectroscopy (IFS) surveys (e.g. SAURON de Zeeuw et al. Reference de Zeeuw2002; ATLAS3D Cappellari et al. Reference Cappellari2011; CALIFA Sánchez et al. Reference Sánchez2012; SAMI Croom et al. Reference Croom2012; MANGA Bundy et al. Reference Bundy2015) over the past two decades has enabled two-dimensional stellar kinematic maps of galaxies to be determined, a significant improvement on traditional long-slit spectroscopy. The prevalence of available spatial information from IFS surveys has motivated the introduction of the spin parameter proxy
![]() $\lambda_R$
by Emsellem et al. (Reference Emsellem2007):
$\lambda_R$
by Emsellem et al. (Reference Emsellem2007):
![]() $\lambda_R \equiv \langle R \vert V \vert \rangle / \langle R\sqrt{ V^2 + \sigma^2}\rangle$
, quantifying the amount of ordered (V) to random (
$\lambda_R \equiv \langle R \vert V \vert \rangle / \langle R\sqrt{ V^2 + \sigma^2}\rangle$
, quantifying the amount of ordered (V) to random (
![]() $\sigma$
) stellar motion, where the radius R is typically the effective radius
$\sigma$
) stellar motion, where the radius R is typically the effective radius
![]() $R_e$
.
$R_e$
.
![]() $\lambda_R$
, in conjunction with ellipticity, has consequently revealed a small, distinct population of dispersion-dominated slow rotators (SRs), in contrast to a rotationally-supported population of fast rotators (FRs) (Emsellem et al. Reference Emsellem2007). Across all morphology types the fraction of SRs,
$\lambda_R$
, in conjunction with ellipticity, has consequently revealed a small, distinct population of dispersion-dominated slow rotators (SRs), in contrast to a rotationally-supported population of fast rotators (FRs) (Emsellem et al. Reference Emsellem2007). Across all morphology types the fraction of SRs,
![]() $f_{SR} \lesssim 0.1$
(e.g. van de Sande et al. Reference van de Sande2021b; Fraser-McKelvie & Cortese Reference Fraser-McKelvie and Cortese2022), whereas when only including early-types
$f_{SR} \lesssim 0.1$
(e.g. van de Sande et al. Reference van de Sande2021b; Fraser-McKelvie & Cortese Reference Fraser-McKelvie and Cortese2022), whereas when only including early-types
![]() $f_{SR} \approx 0.15$
(Emsellem et al. Reference Emsellem2011; Brough et al. Reference Brough2017; van de Sande et al. Reference van de Sande2021b). Indeed, SRs are predominantly massive ellipticals: observational studies have identified a strong correlation between
$f_{SR} \approx 0.15$
(Emsellem et al. Reference Emsellem2011; Brough et al. Reference Brough2017; van de Sande et al. Reference van de Sande2021b). Indeed, SRs are predominantly massive ellipticals: observational studies have identified a strong correlation between
![]() $f_{SR}$
and stellar mass, particularly above
$f_{SR}$
and stellar mass, particularly above
![]() $M_{\ast} = 10^{11} M_{\odot}$
where
$M_{\ast} = 10^{11} M_{\odot}$
where
![]() $f_{SR} \approx 0.4$
(Emsellem et al. Reference Emsellem2011; van de Sande et al. Reference van de Sande2021b), with additional support from simulations (Lagos et al. Reference Lagos2018).
$f_{SR} \approx 0.4$
(Emsellem et al. Reference Emsellem2011; van de Sande et al. Reference van de Sande2021b), with additional support from simulations (Lagos et al. Reference Lagos2018).
In our current picture of galaxy formation and evolution, galaxy-galaxy mergers are the primary means by which high mass (
![]() $M_{\ast} \gtrsim 10^{10.5} M_{\odot}$
) galaxies accrete additional mass (e.g. Robotham et al. Reference Robotham2014). Early work suggests that ellipticals form via major merging (e.g. Toomre Reference Toomre, Tinsley, Larson and Richard1977; Navarro & Benz Reference Navarro and Benz1991; Hernquist Reference Hernquist1993). In addition, later work also suggests that multiple dry minor mergers are another pathway for elliptical formation (Naab et al. Reference Naab2014; Moody et al. Reference Moody, Romanowsky, Cox, Novak and Primack2014; Schulze et al. Reference Schulze2018). This suggests that merging plays a key role in SR formation.
$M_{\ast} \gtrsim 10^{10.5} M_{\odot}$
) galaxies accrete additional mass (e.g. Robotham et al. Reference Robotham2014). Early work suggests that ellipticals form via major merging (e.g. Toomre Reference Toomre, Tinsley, Larson and Richard1977; Navarro & Benz Reference Navarro and Benz1991; Hernquist Reference Hernquist1993). In addition, later work also suggests that multiple dry minor mergers are another pathway for elliptical formation (Naab et al. Reference Naab2014; Moody et al. Reference Moody, Romanowsky, Cox, Novak and Primack2014; Schulze et al. Reference Schulze2018). This suggests that merging plays a key role in SR formation.
Indeed, modelling by Khochfar et al. (Reference Khochfar2011) found that SRs have typically experienced more than twice as many major mergers than FRs. Binary merger simulations of disk galaxies by Bois et al. (Reference Bois2011) showed that minor disk-disk mergers almost always produced a fast rotator, whereas, major mergers in these simulations were able to produce both FRs and SRs. Simulations by Schulze et al. (Reference Schulze2018) found that about half of the SRs are formed rapidly (in
![]() $\sim 0.5$
Gyr) through major mergers, while the other half have a different formation history not involving major mergers. Additionally, simulations have shown that the amount of gas involved in the merger appears to play a key role in the stellar kinematics of the remnant (e.g. Hoffman et al. Reference Hoffman, Cox, Dutta and Hernquist2010; Naab et al. Reference Naab2014; Lagos et al. Reference Lagos2018; Lagos et al. Reference Lagos2022). Gas-rich (wet) mergers were more likely to spin-up the merger remnant, due to the gas cooling and reforming a disk, with gas-poor (dry) mergers tending to have the opposite effect. Interestingly, Lagos et al. (Reference Lagos2022) also found that about 15% of low mass (
$\sim 0.5$
Gyr) through major mergers, while the other half have a different formation history not involving major mergers. Additionally, simulations have shown that the amount of gas involved in the merger appears to play a key role in the stellar kinematics of the remnant (e.g. Hoffman et al. Reference Hoffman, Cox, Dutta and Hernquist2010; Naab et al. Reference Naab2014; Lagos et al. Reference Lagos2018; Lagos et al. Reference Lagos2022). Gas-rich (wet) mergers were more likely to spin-up the merger remnant, due to the gas cooling and reforming a disk, with gas-poor (dry) mergers tending to have the opposite effect. Interestingly, Lagos et al. (Reference Lagos2022) also found that about 15% of low mass (
![]() $M_{\ast} \lesssim 10^{10.5} M_{\odot}$
) SRs in EAGLE formed without mergers.
$M_{\ast} \lesssim 10^{10.5} M_{\odot}$
) SRs in EAGLE formed without mergers.
The exact pathway to slow rotator formation, however, is still not fully understood. For instance, the relationship between environment and spin is tenuous. Several studies have detected a weak environmental trend with
![]() $f_{SR}$
(e.g.
$f_{SR}$
(e.g.
![]() $\Sigma_3$
: Cappellari et al. Reference Cappellari2011 and D’Eugenio et al. Reference D’Eugenio, Houghton, Davies and Dalla Bontà2013;
$\Sigma_3$
: Cappellari et al. Reference Cappellari2011 and D’Eugenio et al. Reference D’Eugenio, Houghton, Davies and Dalla Bontà2013;
![]() $\Sigma_5$
: van de Sande et al. Reference van de Sande2021a (fixed
$\Sigma_5$
: van de Sande et al. Reference van de Sande2021a (fixed
![]() $M_{\ast}$
); centrals vs satellites vs isolated galaxies: van de Sande et al. Reference van de Sande2021a (fixed
$M_{\ast}$
); centrals vs satellites vs isolated galaxies: van de Sande et al. Reference van de Sande2021a (fixed
![]() $M_{\ast}$
) and Lagos et al. Reference Lagos2018 (simulations)). That is, SRs are more likely to exist in denser regions than sparser regions. Conversely, after controlling for stellar mass, other studies were unable to find a relationship with environment (centrals vs satellites: Greene et al. Reference Greene2018;
$M_{\ast}$
) and Lagos et al. Reference Lagos2018 (simulations)). That is, SRs are more likely to exist in denser regions than sparser regions. Conversely, after controlling for stellar mass, other studies were unable to find a relationship with environment (centrals vs satellites: Greene et al. Reference Greene2018;
![]() $\Sigma_5$
: Brough et al. Reference Brough2017; see also Veale et al. Reference Veale2018 and Vaughan et al. Reference Vaughan2024). To further complicate matters when studying spin and SR formation, the need for careful consideration of stellar population age has also recently become apparent (van de Sande et al. Reference van de Sande2018; Croom et al. Reference Croom2024; Rutherford et al. Reference Rutherford2024).
$\Sigma_5$
: Brough et al. Reference Brough2017; see also Veale et al. Reference Veale2018 and Vaughan et al. Reference Vaughan2024). To further complicate matters when studying spin and SR formation, the need for careful consideration of stellar population age has also recently become apparent (van de Sande et al. Reference van de Sande2018; Croom et al. Reference Croom2024; Rutherford et al. Reference Rutherford2024).
A particular class of galaxy systems known as fossil groups (FGs; Ponman et al. Reference Ponman1994) are expected to have an extensive intra-group merger history. That is, most of the satellites have infallen via dynamical friction and merged with the central. These highly dynamically evolved systems are characterised by their low group multiplicity, a central that dominates the group in mass, and an X-ray emitting halo - typical of that of a much larger group or cluster (see Section 3.1 for more detail). Indeed, simulations suggest that, on average, FG centrals undergo more major mergers than non-FG centrals (Kundert, D’Onghia, & Aguerri Reference Kundert, D’Onghia and Aguerri2017). For a full review on the formation and evolution of fossil groups see Aguerri & Zarattini (Reference Aguerri and Zarattini2021).
The aim of our investigation is to further explore the merger hypothesis for slow rotator formation, focusing our attention on dynamically evolved groups. We wish to compare the stellar kinematic properties of the centrals of dynamically evolved groups to the centrals of groups that are not dynamically evolved. To this end, we make use of observational catalogue data from SAMI in conjunction with ancillary group data from GAMA (Driver et al. Reference Driver2011), as well as data from the EAGLE (Schaye et al. Reference Schaye2015; Crain et al. Reference Crain2015; McAlpine et al. Reference McAlpine2016) and Magneticum Pathfinder (Dolag et al. Reference Dolag, Borgani, Murante and Springel2009a; Hirschmann et al. Reference Hirschmann2014) simulations (see Section 2 for more detail).
This paper is structured as follows. We describe the input data used in Section 2. In Section 3 we outline our approach to identifying fossil and mass gap groups. In Section 4 we present our findings regarding their stellar kinematic properties. We discuss our results in Section 5 and conclude in Section 6. Unless otherwise stated, we assume a cosmology with
![]() $\Omega_m = 0.3$
,
$\Omega_m = 0.3$
,
![]() $\Omega_{\Lambda} = 0.7$
and
$\Omega_{\Lambda} = 0.7$
and
![]() $H_0 = 70\text{km s}^{-1} \text{Mpc}^{-1}$
.
$H_0 = 70\text{km s}^{-1} \text{Mpc}^{-1}$
.
2. Input data
2.1. The GAMA Galaxy Survey
Commencing in 2008 and completing in 2014, the Galaxy And Mass Assembly (GAMA; Driver et al. Reference Driver2011) survey combines multi-wavelength photometric data with a spectroscopic survey conducted with the 3.9 m Anglo-Australian Telescope (AAT) using the AAOmega multi-object spectrograph. As part of GAMA the AAT observed
![]() $\approx$
300 000 galaxies over
$\approx$
300 000 galaxies over
![]() $286 \text{ deg}^2$
, achieving a limiting magnitude
$286 \text{ deg}^2$
, achieving a limiting magnitude
![]() $r_{AB} \approx 19.8$
mag and a completeness in excess of 98% in the equatorial regions.
$r_{AB} \approx 19.8$
mag and a completeness in excess of 98% in the equatorial regions.
We make use of GAMA data release 4 from the GAMA II survey (Baldry et al. Reference Baldry2018; Driver et al. Reference Driver2022) in our investigation, for the three equatorial fields: G09, G12 and G15. In particular, we use the stellar mass, halo mass and group member identification data products.
About 40% of galaxies in GAMA are assigned to a particular galaxy group. Grouping is accomplished using a friends-of-friends grouping algorithm which was quality tested on a mock galaxy catalogue using the Millennium simulation (Springel et al. Reference Springel2005). In essence, galaxies are linked based on both their projected and radial separations (see Robotham et al. Reference Robotham2011 for more detail).
Stellar mass estimates are based on stellar population synthesis modelling by Bruzual & Charlot (Reference Bruzual and Charlot2003) (see Taylor et al. Reference Taylor2011, for more detail) and do not include flux scale corrections (which can add significant noise to the aperture based stellar mass estimates). Halo masses in GAMA were estimated based on the group velocity dispersion,
![]() $\sigma$
, and the radius containing 50% of group members, R. That is,
$\sigma$
, and the radius containing 50% of group members, R. That is,
![]() $M_{halo} = A \sigma^2R$
to first order, where the scaling factor
$M_{halo} = A \sigma^2R$
to first order, where the scaling factor
![]() $A = 10.0$
was calibrated with simulations (Robotham et al. Reference Robotham2011). GAMA data is available at http://www.gama-survey.org/.
$A = 10.0$
was calibrated with simulations (Robotham et al. Reference Robotham2011). GAMA data is available at http://www.gama-survey.org/.
2.2. The SAMI Galaxy Survey
The SAMI Galaxy Survey (Croom et al. Reference Croom2012) derives its name from the Sydney-AAO Multi-object Integral-Field Spectrograph, also installed on the AAT, which was used to observe about 3 000 galaxies at low redshift (
![]() $z \lesssim 0.1$
). About 75% of these galaxies come from the three equatorial regions of GAMA, providing a wealth of ancillary data for the SAMI catalogue, with the remaining galaxies selected from several cluster regions (Bryant et al. Reference Bryant2015; Owers et al. Reference Owers2017).
$z \lesssim 0.1$
). About 75% of these galaxies come from the three equatorial regions of GAMA, providing a wealth of ancillary data for the SAMI catalogue, with the remaining galaxies selected from several cluster regions (Bryant et al. Reference Bryant2015; Owers et al. Reference Owers2017).
The SAMI instrument consists of an array of 13 hexabundles (Bland-Hawthorn et al. Reference Bland-Hawthorn2011; Bryant et al. Reference Bryant, O’Byrne, Bland-Hawthorn and Leon-Saval2011; Bryant et al. Reference Bryant, Bland-Hawthorn, Fogarty, Lawrence and Croom2014), each consisting of 61 optical fibres. With each hexabundle able to observe a different object, SAMI was capable of sampling a much greater number of galaxies in a given amount of time than its predecessors.
Reduction of SAMI data is performed primarily using the 2
![]() $\text{DF}$
data reduction package (AAO software team 2015) and the SAMI
$\text{DF}$
data reduction package (AAO software team 2015) and the SAMI
![]() $\text{PYTHON}$
package (Allen et al. Reference Allen2014). For each observed galaxy, collected data is organised into cubes (Sharp et al. Reference Sharp2015; Scott et al. Reference Scott2018) comprised of 50
$\text{PYTHON}$
package (Allen et al. Reference Allen2014). For each observed galaxy, collected data is organised into cubes (Sharp et al. Reference Sharp2015; Scott et al. Reference Scott2018) comprised of 50
![]() $\times$
50 spatial pixels (pixel side length 0.5 arcsec) and 2 048 wavelengths. There are two primary data cubes for each galaxy corresponding to the blue (370–570 nm) and red (630–740 nm) wavelength ranges.
$\times$
50 spatial pixels (pixel side length 0.5 arcsec) and 2 048 wavelengths. There are two primary data cubes for each galaxy corresponding to the blue (370–570 nm) and red (630–740 nm) wavelength ranges.
In our investigation we use stellar kinematic and (light-weighted) age data from SAMI data release 3 (Croom et al. Reference Croom2021). SAMI stellar kinematic measurements were performed using penalized PiXel-Fitting (pPXF) (Cappellari & Emsellem Reference Cappellari and Emsellem2004; Cappellari Reference Cappellari2017) (for more detail see van de Sande et al. Reference van de Sande2017a). We use the
![]() $\lambda_{Re}$
data that has been corrected for both seeing (Harborne et al. Reference Harborne2020) and aperture (van de Sande et al. Reference van de Sande2017b) effects.
$\lambda_{Re}$
data that has been corrected for both seeing (Harborne et al. Reference Harborne2020) and aperture (van de Sande et al. Reference van de Sande2017b) effects.
![]() $R_e$
and ellipticity (
$R_e$
and ellipticity (
![]() $\epsilon$
) measurements were calculated using Multi Gaussian Expansion (MGE) fits (Emsellem et al. Reference Emsellem, Monnet, Bacon and Nieto1994; Cappellari Reference Cappellari2002). Vaughan et al. (Reference Vaughan2022) describe age measurements made for SAMI using stellar population synthesis modelling. SAMI catalogue data and documentation can be found at https://datacentral.org.au/.
$\epsilon$
) measurements were calculated using Multi Gaussian Expansion (MGE) fits (Emsellem et al. Reference Emsellem, Monnet, Bacon and Nieto1994; Cappellari Reference Cappellari2002). Vaughan et al. (Reference Vaughan2022) describe age measurements made for SAMI using stellar population synthesis modelling. SAMI catalogue data and documentation can be found at https://datacentral.org.au/.
2.3. EAGLE simulations
EAGLE (Evolution and Assembly of GaLaxies and their Environments; Schaye et al. Reference Schaye2015; Crain et al. Reference Crain2015; McAlpine et al. Reference McAlpine2016) is a collection of hydrodynamical simulations exploring supermassive black hole (BH) and galaxy formation in cosmologically representative volumes (25–100 comoving Mpc). EAGLE assumes the cosmological parameter values determined by Planck Collaboration XVI (Planck Collaboration et al. Reference Collaboration2014):
![]() $\Omega_{\Lambda} = 0.693$
,
$\Omega_{\Lambda} = 0.693$
,
![]() $\Omega_{\text{m}} = 0.307$
,
$\Omega_{\text{m}} = 0.307$
,
![]() $\Omega_{\text{b}} = 0.04825$
,
$\Omega_{\text{b}} = 0.04825$
,
![]() $\text{H}_0 = 67.77 \text{ km s}^{-1} \text{Mpc}^{-1}$
, and
$\text{H}_0 = 67.77 \text{ km s}^{-1} \text{Mpc}^{-1}$
, and
![]() $\sigma_8 = 0.8288$
. EAGLE employs sub-grid models for a range of physical processes including radiative cooling, stellar formation and evolution, BH gas accretion, and feedback. For a comprehensive discussion on EAGLE sub-grid physics see Crain et al. (Reference Crain2015).
$\sigma_8 = 0.8288$
. EAGLE employs sub-grid models for a range of physical processes including radiative cooling, stellar formation and evolution, BH gas accretion, and feedback. For a comprehensive discussion on EAGLE sub-grid physics see Crain et al. (Reference Crain2015).
Ref-L0100N1504 was the particular EAGLE simulation used in our investigation. Ref-L0100N1504 has a box side length of 100 comoving Mpc, 700 pc spatial resolution, consists of
![]() $2 \times 1504^3$
particles with an initial baryonic particle mass of
$2 \times 1504^3$
particles with an initial baryonic particle mass of
![]() $1.81 \times 10^6 M_{\odot}$
and a dark matter particle mass of
$1.81 \times 10^6 M_{\odot}$
and a dark matter particle mass of
![]() $9.70 \times 10^6 M_{\odot}$
(McAlpine et al. Reference McAlpine2016). A galaxy’s stellar mass is taken to be the total star particle mass associated with the galaxy’s subhalo within a 3D aperture of radius 30 proper kpc. In addition, feedback was calibrated to match the observed galaxy stellar mass function at
$9.70 \times 10^6 M_{\odot}$
(McAlpine et al. Reference McAlpine2016). A galaxy’s stellar mass is taken to be the total star particle mass associated with the galaxy’s subhalo within a 3D aperture of radius 30 proper kpc. In addition, feedback was calibrated to match the observed galaxy stellar mass function at
![]() $z=0$
(Schaye et al. Reference Schaye2015).
$z=0$
(Schaye et al. Reference Schaye2015).
We use the stellar kinematic measurements of EAGLE galaxies by Lagos et al. (Reference Lagos2018), which were performed using a similar approach as in SAMI (van de Sande et al. Reference van de Sande2017a; see also van de Sande et al. Reference van de Sande2019). Briefly, Lagos et al. (Reference Lagos2018) create two-dimensional stellar kinematic and luminosity maps for each galaxy with pixel width 1.5 proper kpc (c.f. 1.6 proper kpc at
![]() $z = 0.05$
for SAMI; van de Sande et al. Reference van de Sande2017b). From these maps, r-band flux-weighted ellipticity (
$z = 0.05$
for SAMI; van de Sande et al. Reference van de Sande2017b). From these maps, r-band flux-weighted ellipticity (
![]() $\epsilon$
) and proxy spin parameter (
$\epsilon$
) and proxy spin parameter (
![]() $\lambda_{R}$
) can then be determined. EAGLE data are publicly available and can be found at http://icc.dur.ac.uk/Eagle/database.php
$\lambda_{R}$
) can then be determined. EAGLE data are publicly available and can be found at http://icc.dur.ac.uk/Eagle/database.php
2.4. Magneticum Pathfinder simulations
Magneticum Pathfinder (Magneticum; Dolag et al. Reference Dolag, Borgani, Murante and Springel2009a; Hirschmann et al. Reference Hirschmann2014) are another set of cosmological hydrodynamical simulations which were run using GADGET-3, an extension of GADGET-2 (Springel et al. Reference Springel2005). Magneticum adopts the Wilkinson Microwave Anisotropy Probe (Komatsu et al. Reference Komatsu2011) cosmological parameters:
![]() $\Omega_{\Lambda} = 0.728$
,
$\Omega_{\Lambda} = 0.728$
,
![]() $\Omega_{\text{m}} = 0.272$
,
$\Omega_{\text{m}} = 0.272$
,
![]() $\Omega_{\text{b}} = 0.0451$
,
$\Omega_{\text{b}} = 0.0451$
,
![]() $\text{H}_0 = 70.4 \text{ km s}^{-1} \text{Mpc}^{-1}$
, and
$\text{H}_0 = 70.4 \text{ km s}^{-1} \text{Mpc}^{-1}$
, and
![]() $\sigma_8 = 0.809$
. Magneticum also incorporates a plethora of sub-grid physics including gas cooling and star formation (Springel & Hernquist Reference Springel and Hernquist2003), stellar and chemical evolution (Tornatore et al. Reference Tornatore, Borgani, Dolag and Matteucci2007), magnetic fields (Dolag et al. Reference Dolag, Stasyszyn, Donnert, Pakmor, Strassmeier, Kosovichev and Beckman2009b), and black holes and AGN feedback (Springel, Frenk, & White Reference Springel, Frenk and White2006; Fabjan et al. Reference Fabjan2010; Hirschmann et al. Reference Hirschmann2014). For more details on this particular simulation, see also Teklu et al. (Reference Teklu2015).
$\sigma_8 = 0.809$
. Magneticum also incorporates a plethora of sub-grid physics including gas cooling and star formation (Springel & Hernquist Reference Springel and Hernquist2003), stellar and chemical evolution (Tornatore et al. Reference Tornatore, Borgani, Dolag and Matteucci2007), magnetic fields (Dolag et al. Reference Dolag, Stasyszyn, Donnert, Pakmor, Strassmeier, Kosovichev and Beckman2009b), and black holes and AGN feedback (Springel, Frenk, & White Reference Springel, Frenk and White2006; Fabjan et al. Reference Fabjan2010; Hirschmann et al. Reference Hirschmann2014). For more details on this particular simulation, see also Teklu et al. (Reference Teklu2015).
In this study we use galaxy catalogue data from snapshot 136 (
![]() $z=0.066$
) of the ultra high resolution ‘Box4’ simulation of Magneticum. Box4 has a box side length of 68 comoving Mpc, initially
$z=0.066$
) of the ultra high resolution ‘Box4’ simulation of Magneticum. Box4 has a box side length of 68 comoving Mpc, initially
![]() $2\times 576^3$
particles with dark matter particle mass
$2\times 576^3$
particles with dark matter particle mass
![]() $3.6 \times 10^7 M_{\odot}h^{-1}$
and gas particle initial mass
$3.6 \times 10^7 M_{\odot}h^{-1}$
and gas particle initial mass
![]() $7.3 \times 10^6 M_{\odot}h^{-1}$
. Galaxies in Magneticum were identified using subfind (Springel et al. Reference Springel, White, Tormen and Kauffmann2001), which includes the stellar halo of the group in the total stellar mass of the central.
$7.3 \times 10^6 M_{\odot}h^{-1}$
. Galaxies in Magneticum were identified using subfind (Springel et al. Reference Springel, White, Tormen and Kauffmann2001), which includes the stellar halo of the group in the total stellar mass of the central.
We also use the Box4 stellar kinematic products measured by Schulze et al. (Reference Schulze2018). These stellar kinematic measurements were performed using a similar procedure and spatial resolution to that used by Lagos et al. (Reference Lagos2018) for EAGLE, except Schulze et al. (Reference Schulze2018) use a mass-weighted approach and assume a constant mass-to-light ratio across each galaxy. Magneticum data can be found at http://www.magneticum.org and at the web portal https://c2papcosmosim.uc.lrz.de/.
2.5. Sample selection
The full SAMI, EAGLE, and Magneticum group samples in the central stellar mass-halo mass plane can be seen in Fig. 1. Our observational sample consists of galaxy groups in the equatorial GAMA fields (G09, G12, G15) for which there is reliable SAMI stellar kinematic data for the central - taken to be the most massive galaxy. Groups containing galaxies with missing stellar mass estimates are discarded to avoid potentially misleading mass gap calculations (see Section 3.1). For SAMI galaxies with repeat observations we choose the datacube pair with the higher signal-to-noise ratio that has been less affected by seeing conditions.
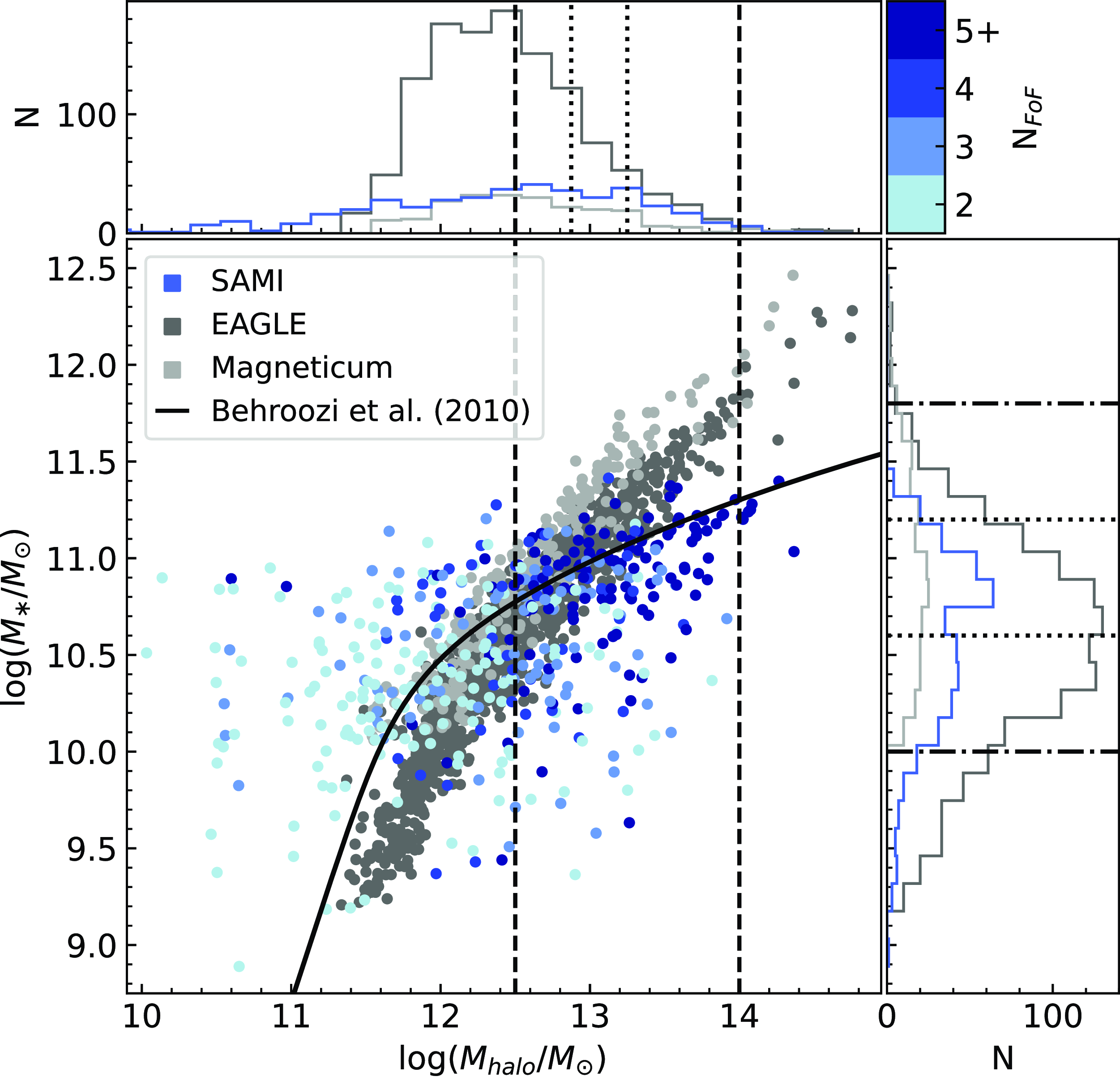
Figure 1. Central stellar mass vs. halo mass for the full group samples of SAMI (blue, good kinematic data for group central and no missing satellite stellar mass data only), EAGLE (dark grey), and Magneticum (light grey). A best-fit stellar mass - halo mass relation by Behroozi, Conroy, & Wechsler (Reference Behroozi, Conroy and Wechsler2010) is shown in solid black. Halo mass cuts are shown by the dashed lines, where our final SAMI, EAGLE, and Magneticum samples are contained within. Dotted lines demarcate the bins used when binning by stellar mass or halo mass. Dash-dotted lines are the minimum and maximum stellar mass bin boundaries, but are not a general cut on the full samples. Group multiplicity
![]() $N_{FoF}$
is shown for SAMI (blue shades), indicating that most low halo mass groups are galaxy pairs whose halo masses are difficult to measure.
$N_{FoF}$
is shown for SAMI (blue shades), indicating that most low halo mass groups are galaxy pairs whose halo masses are difficult to measure.
Since we identify dynamically evolved groups in our sample based on their mass gap and halo mass, we do not consider isolated galaxies in our investigation. It is perhaps possible that an isolated galaxy could be an extreme fossil group, where all of the satellites have merged with the central. However, we did not detect any isolated galaxies in our EAGLE or Magneticum samples with a halo mass above our threshold for fossil groups. Hence, extreme fossil groups are likely exceedingly rare in the current epoch.
Fig. 1 reveals significant scatter in the stellar mass - halo mass plane for SAMI, largely due to measurement errors and uncertainties. In contrast, tight relations can be seen for EAGLE and Magneticum. At the very high mass end, simulations also tend to add more stellar mass to the galaxy than observed. This is a problem of too many stars in EAGLE and Magneticum, as well as these simulations adding all stripped stars to the central galaxy (Remus & Forbes Reference Remus and Forbes2022). For a detailed comparison of dynamical properties between EAGLE, Magneticum and SAMI, see van de Sande et al. (Reference van de Sande2019) who find the relationship between dynamical mass and stellar mass is broadly consistent between the data and simulations (e.g. their Fig. 6).
We restrict our analysis to galaxy groups with
![]() $12.5 \unicode{x003C}$
log(
$12.5 \unicode{x003C}$
log(
![]() $M_{halo}$
/
$M_{halo}$
/
![]() $M_{\odot}$
)
$M_{\odot}$
)
![]() $\unicode{x003C} 14$
, for the following reasons. Firstly, van de Sande et al. (Reference van de Sande2021a) find that below this range, the halo mass function of the SAMI survey deviates considerably from simulation-based predictions by Angulo et al. (Reference Angulo2012). Secondly, we found that our SAMI sample for log(
$\unicode{x003C} 14$
, for the following reasons. Firstly, van de Sande et al. (Reference van de Sande2021a) find that below this range, the halo mass function of the SAMI survey deviates considerably from simulation-based predictions by Angulo et al. (Reference Angulo2012). Secondly, we found that our SAMI sample for log(
![]() $M_{halo}$
/
$M_{halo}$
/
![]() $M_{\odot}$
)
$M_{\odot}$
)
![]() $\unicode{x003C} 12.5$
was dominated by galaxy pairs, whose halo masses are difficult to estimate and were hence contaminating our sample. Lastly, we impose the upper halo mass bound due to a statistically insignificant sample above this value. The number of galaxy groups in our final SAMI, EAGLE, and Magneticum samples are 201, 501, and 115, respectively.
$\unicode{x003C} 12.5$
was dominated by galaxy pairs, whose halo masses are difficult to estimate and were hence contaminating our sample. Lastly, we impose the upper halo mass bound due to a statistically insignificant sample above this value. The number of galaxy groups in our final SAMI, EAGLE, and Magneticum samples are 201, 501, and 115, respectively.
3. Methods
3.1. Identifying dynamically evolved groups
A more formal definition for fossil groups than the qualitative description by Ponman et al. (Reference Ponman1994) was proposed by Jones et al. (Reference Jones2003), based on the following two criteria:
-
1.
 $\Delta m_{12} \geq 2.0$
mag, where
$\Delta m_{12} \geq 2.0$
mag, where
 $\Delta m_{12}$
is the difference in absolute magnitude in the r-band between the two brightest galaxies in the group.
$\Delta m_{12}$
is the difference in absolute magnitude in the r-band between the two brightest galaxies in the group. -
2.
 $\text{L}_{X,bol} \geq 0.25 \times 10^{42} \text{ erg s}^{-1}$
, where
$\text{L}_{X,bol} \geq 0.25 \times 10^{42} \text{ erg s}^{-1}$
, where
 $\text{L}_{X,bol}$
is the bolometric X-ray luminosity in the ‘soft’ (0.5–2 keV) band. Gas is confined in the halo’s potential, which depends on halo mass, and is consequently heated to the virial temperature (Ghirardini et al. Reference Ghirardini2019). In addition, halo mass is conserved under the merger process. Hence, galaxy groups with few members that are dominated by a single galaxy and are contained within a massive halo, typical of that of a much larger group/cluster, suggest an extensive merger history.
$\text{L}_{X,bol}$
is the bolometric X-ray luminosity in the ‘soft’ (0.5–2 keV) band. Gas is confined in the halo’s potential, which depends on halo mass, and is consequently heated to the virial temperature (Ghirardini et al. Reference Ghirardini2019). In addition, halo mass is conserved under the merger process. Hence, galaxy groups with few members that are dominated by a single galaxy and are contained within a massive halo, typical of that of a much larger group/cluster, suggest an extensive merger history.
These two criteria are typically adopted in the literature as necessary and sufficient conditions for identifying fossil groups (e.g. D’Onghia et al. Reference D’Onghia2005; Dariush et al. Reference Dariush2007; Khosroshahi, Jones, & Ponman Reference Khosroshahi, Jones and Ponman2004; Mendes de Oliveira et al. Reference Mendes de Oliveira, Cypriano, Dupke and Sodrà2009; Zarattini et al. Reference Zarattini2014). Some authors such as Kundert et al. (Reference Kundert, D’Onghia and Aguerri2017) used halo mass
![]() $M_{halo}$
instead of
$M_{halo}$
instead of
![]() $\text{L}_{X,bol}$
. We will do the same in our approach to fossil group identification due to a lack of X-ray luminosity data for most of our sample. Therefore, the fossil groups identified in our study may not represent prototypical fossil groups identified by Jones et al. (Reference Jones2003) and others, but rather highly dynamically evolved systems. Additionally, some authors (e.g. Dariush et al. Reference Dariush2007) also explored systems that satisfy only the magnitude gap criterion, labelling them optical fossil groups, as weaker evidence for a dynamically evolved system. We adopt a similar approach in our investigation, except we refer to them as mass gap groups, since we use stellar mass in lieu of r-band magnitude. Finally, it is worth noting that the cut-off values for these conditions are somewhat arbitrary, by Jones et al. (Reference Jones2003)’s own admission.
$\text{L}_{X,bol}$
. We will do the same in our approach to fossil group identification due to a lack of X-ray luminosity data for most of our sample. Therefore, the fossil groups identified in our study may not represent prototypical fossil groups identified by Jones et al. (Reference Jones2003) and others, but rather highly dynamically evolved systems. Additionally, some authors (e.g. Dariush et al. Reference Dariush2007) also explored systems that satisfy only the magnitude gap criterion, labelling them optical fossil groups, as weaker evidence for a dynamically evolved system. We adopt a similar approach in our investigation, except we refer to them as mass gap groups, since we use stellar mass in lieu of r-band magnitude. Finally, it is worth noting that the cut-off values for these conditions are somewhat arbitrary, by Jones et al. (Reference Jones2003)’s own admission.
3.1.1. Mass gap definition and threshold
As alluded to above, we take a stellar-mass-based approach to identifying dynamically evolved groups, i.e. mass gap groups and fossil groups. We define the mass gap of a group to be
![]() $\Delta m_{1\bar{23}}$
: the difference between the most massive galaxy - the central – and the mean of the two most massive satellites, as it is less susceptible to scatter in the mass function than
$\Delta m_{1\bar{23}}$
: the difference between the most massive galaxy - the central – and the mean of the two most massive satellites, as it is less susceptible to scatter in the mass function than
![]() $\Delta m_{12}$
. Indeed, some studies (e.g. Zhoolideh Haghighi et al. Reference Zhoolideh Haghighi, Raouf, Khosroshahi, Farhang and Gozaliasl2020) used
$\Delta m_{12}$
. Indeed, some studies (e.g. Zhoolideh Haghighi et al. Reference Zhoolideh Haghighi, Raouf, Khosroshahi, Farhang and Gozaliasl2020) used
![]() $\Delta m_{14}$
instead, with Aguerri & Zarattini (Reference Aguerri and Zarattini2021) arguing that it is a more reliable metric than
$\Delta m_{14}$
instead, with Aguerri & Zarattini (Reference Aguerri and Zarattini2021) arguing that it is a more reliable metric than
![]() $\Delta m_{12}$
.
$\Delta m_{12}$
.
By fitting a curve to our sample in the stellar mass - luminosity plane, we find that Jones et al. (Reference Jones2003)’s magnitude gap threshold of 2.0 mag corresponds to a mass gap threshold of 0.97 log
![]() $(M_{\ast}$
/
$(M_{\ast}$
/
![]() $M_{\odot})$
.
$M_{\odot})$
.
3.1.2. Determining the halo mass threshold
Given the lack of available X-ray luminosity data for our sample, we used halo mass estimates from GAMA in lieu of
![]() $L_{X,bol}$
and related the two quantities using a combination of two approaches. The first was based on work by Dariush et al. (Reference Dariush2007) using data from the Millennium gas simulation (based on the Millennium simulation by Springel et al. Reference Springel2005). Dariush et al. (Reference Dariush2007) determined a relation between bolometric X-ray luminosity and dark matter halo mass, predicting a halo mass cut-off for fossil groups of
$L_{X,bol}$
and related the two quantities using a combination of two approaches. The first was based on work by Dariush et al. (Reference Dariush2007) using data from the Millennium gas simulation (based on the Millennium simulation by Springel et al. Reference Springel2005). Dariush et al. (Reference Dariush2007) determined a relation between bolometric X-ray luminosity and dark matter halo mass, predicting a halo mass cut-off for fossil groups of
![]() $\sim$
13.25–13.5
$\sim$
13.25–13.5
![]() $\text{log}(M_{halo}/M_{\odot}$
).
$\text{log}(M_{halo}/M_{\odot}$
).
For the second approach we used the following observationally determined
![]() $L_x-M_{halo}$
relation by Bulbul et al. (Reference Bulbul2019) based on galaxy cluster data from the South Pole Telescope-Sunyaev-Zel’dovich survey (SPT-SZ; Bleem et al. Reference Bleem2015):
$L_x-M_{halo}$
relation by Bulbul et al. (Reference Bulbul2019) based on galaxy cluster data from the South Pole Telescope-Sunyaev-Zel’dovich survey (SPT-SZ; Bleem et al. Reference Bleem2015):
where
![]() $A_X=4.15\times 10^{44}\text{ erg s}^{-1}$
,
$A_X=4.15\times 10^{44}\text{ erg s}^{-1}$
,
![]() $B_X=1.91$
, and
$B_X=1.91$
, and
![]() $\gamma_x = 0.252$
based on fits by Klein et al. (Reference Klein2022) for the eROSITA Final Equatorial Depth Survey (eFEDS; Brunner et al. Reference Brunner2022, which overlaps with the G09 GAMA region);
$\gamma_x = 0.252$
based on fits by Klein et al. (Reference Klein2022) for the eROSITA Final Equatorial Depth Survey (eFEDS; Brunner et al. Reference Brunner2022, which overlaps with the G09 GAMA region);
![]() $M_{piv} = 6.35\times 10^{14}\,\mathrm{M}_{\odot}$
;
$M_{piv} = 6.35\times 10^{14}\,\mathrm{M}_{\odot}$
;
![]() $z_{piv}=0.45$
;
$z_{piv}=0.45$
;
![]() $E(z)=\sqrt{\Omega_M(1+z)^3+\Omega_{\Lambda}}$
. We chose
$E(z)=\sqrt{\Omega_M(1+z)^3+\Omega_{\Lambda}}$
. We chose
![]() $z=0.05$
based on the distribution of redshifts for galaxies in the SAMI catalogue (Croom et al. Reference Croom2021). To convert from
$z=0.05$
based on the distribution of redshifts for galaxies in the SAMI catalogue (Croom et al. Reference Croom2021). To convert from
![]() $L_X$
to
$L_X$
to
![]() $L_{\text{X,bol}}$
, we used eFEDS data (in the soft band, i.e. 0.5–2 keV) to find a linear relation for the two quantities. Consequently, we found that the threshold
$L_{\text{X,bol}}$
, we used eFEDS data (in the soft band, i.e. 0.5–2 keV) to find a linear relation for the two quantities. Consequently, we found that the threshold
![]() $L_{X,bol}=0.25\times 10^{42}\text{ erg s}^{-1}$
corresponded to
$L_{X,bol}=0.25\times 10^{42}\text{ erg s}^{-1}$
corresponded to
![]() $L_{X}=1.6\times 10^{41}\text{ erg s}^{-1}$
, and hence
$L_{X}=1.6\times 10^{41}\text{ erg s}^{-1}$
, and hence
![]() $\text{log}(M_{halo}/M_{\odot}) = 13.13$
.
$\text{log}(M_{halo}/M_{\odot}) = 13.13$
.
The halo mass cuts determined using relations by Dariush et al. (Reference Dariush2007) and Bulbul et al. (Reference Bulbul2019) slightly disagree, which is perhaps unsurprising given some of their differences: assumed cosmology, redshift range covered, and simulation vs observation study type, to name a few. A halo mass threshold
![]() $\text{log}(M_{halo}/M_{\odot}) \geq$
13.25 as a condition for a group to be considered a fossil group was ultimately selected as a good compromise. For comparison, Kundert et al. (Reference Kundert, D’Onghia and Aguerri2017) used a lower bound of
$\text{log}(M_{halo}/M_{\odot}) \geq$
13.25 as a condition for a group to be considered a fossil group was ultimately selected as a good compromise. For comparison, Kundert et al. (Reference Kundert, D’Onghia and Aguerri2017) used a lower bound of
![]() $\text{log}(M_{halo}/M_{\odot}) = 13.15$
in their fossil group study.
$\text{log}(M_{halo}/M_{\odot}) = 13.15$
in their fossil group study.
3.2. Slow rotator identification
For identifying slow rotating galaxies in the SAMI sample, we adopt the SAMI-optimised slow rotator selection criteria defined by van de Sande et al. (Reference van de Sande2021a):
where
![]() $\lambda_{R start} = 0.12$
. Note that other (albeit qualitatively very similar) selection criteria do exist, e.g.
$\lambda_{R start} = 0.12$
. Note that other (albeit qualitatively very similar) selection criteria do exist, e.g.
![]() $\lambda_{Re} \unicode{x003C} 0.1$
(Emsellem et al. Reference Emsellem2007),
$\lambda_{Re} \unicode{x003C} 0.1$
(Emsellem et al. Reference Emsellem2007),
![]() $\lambda_{Re} \unicode{x003C} 0.31 \times \sqrt{\epsilon}$
(Emsellem et al. Reference Emsellem2011) and
$\lambda_{Re} \unicode{x003C} 0.31 \times \sqrt{\epsilon}$
(Emsellem et al. Reference Emsellem2011) and
![]() $\lambda_{Re} \unicode{x003C} 0.08 + \epsilon/4$
,
$\lambda_{Re} \unicode{x003C} 0.08 + \epsilon/4$
,
![]() $\epsilon \unicode{x003C} 0.4$
(Cappellari Reference Cappellari2016).
$\epsilon \unicode{x003C} 0.4$
(Cappellari Reference Cappellari2016).
We only consider the
![]() $f_{SR}$
in our SAMI sample. We avoid identifying SRs in our EAGLE and Magneticum samples following van de Sande et al. (Reference van de Sande2021a)’s findings that SRs in simulations don’t sit in the same part of parameter space as SRs in observations. It is therefore difficult to define a uniform set of SR selection criteria, hence we look at average spin as well.
$f_{SR}$
in our SAMI sample. We avoid identifying SRs in our EAGLE and Magneticum samples following van de Sande et al. (Reference van de Sande2021a)’s findings that SRs in simulations don’t sit in the same part of parameter space as SRs in observations. It is therefore difficult to define a uniform set of SR selection criteria, hence we look at average spin as well.
3.3. Bootstrapping and stellar mass matching
Bootstrapping (Efron Reference Efron1979) is a useful resampling technique when data is limited that allows one to estimate the underlying Probability Density Function (PDF) of the required statistic. For each variable in our investigation, we take N random draws of the relevant sample (i.e. SAMI, EAGLE, or Magneticum) with replacement, where N is the sample size, storing the mean of the resulting bootstrap sample. We then repeat this procedure for 10 000 iterations to generate a PDF for the desired statistic. We report the mean of each resulting PDF and the standard deviation of the bootstrap estimates of the mean is taken to be the uncertainty.
For quantities binned by halo mass, we utilise mass matching to avoid bias due to stellar mass, which we know is strongly correlated to
![]() $\lambda_{Re}$
and
$\lambda_{Re}$
and
![]() $f_{SR}$
(e.g. van de Sande et al. Reference van de Sande2021b). Specifically, for each pair of halo mass bins, every central of a group that is not dynamically evolved has been mass matched within
$f_{SR}$
(e.g. van de Sande et al. Reference van de Sande2021b). Specifically, for each pair of halo mass bins, every central of a group that is not dynamically evolved has been mass matched within
![]() $0.15$
$0.15$
![]() $\text{log}(M_{\ast}/M_{\odot})$
to a unique group central in the corresponding category (fossil group/mass gap group).
$\text{log}(M_{\ast}/M_{\odot})$
to a unique group central in the corresponding category (fossil group/mass gap group).
4. Properties of fossil and mass gap groups
4.1. Prevalence
The combined effect of the mass gap and halo mass cuts on our SAMI sample can be seen in the
![]() $\Delta m_{1\overline{23}}-\text{log}(M_{halo}/M_{\odot})$
plane of Fig. 2. Our SAMI sample was consequently divided into three distinct group classes (Table 1): not dynamically evolved group (NDEG) – galaxy groups with a mass gap below the threshold; mass gap group (MGG) – groups satisfying only the mass gap criterion; and fossil group (FG) – satisfying both the mass gap and halo mass criteria.
$\Delta m_{1\overline{23}}-\text{log}(M_{halo}/M_{\odot})$
plane of Fig. 2. Our SAMI sample was consequently divided into three distinct group classes (Table 1): not dynamically evolved group (NDEG) – galaxy groups with a mass gap below the threshold; mass gap group (MGG) – groups satisfying only the mass gap criterion; and fossil group (FG) – satisfying both the mass gap and halo mass criteria.
Table 1. The number of groups for SAMI, EAGLE, and Magneticum, in each group class category: fossil groups, mass gap groups, and groups that are not dynamically evolved (NDEG). NDEGs have been divided into high and low halo mass at the boundary of
![]() $\log(M_{halo}/M_{\odot})=13.25$
. Numbers in parentheses are the fractions relative to the total number in each halo mass interval, with binomial uncertainties containing the 68% confidence regions (Cameron Reference Cameron2011).
$\log(M_{halo}/M_{\odot})=13.25$
. Numbers in parentheses are the fractions relative to the total number in each halo mass interval, with binomial uncertainties containing the 68% confidence regions (Cameron Reference Cameron2011).

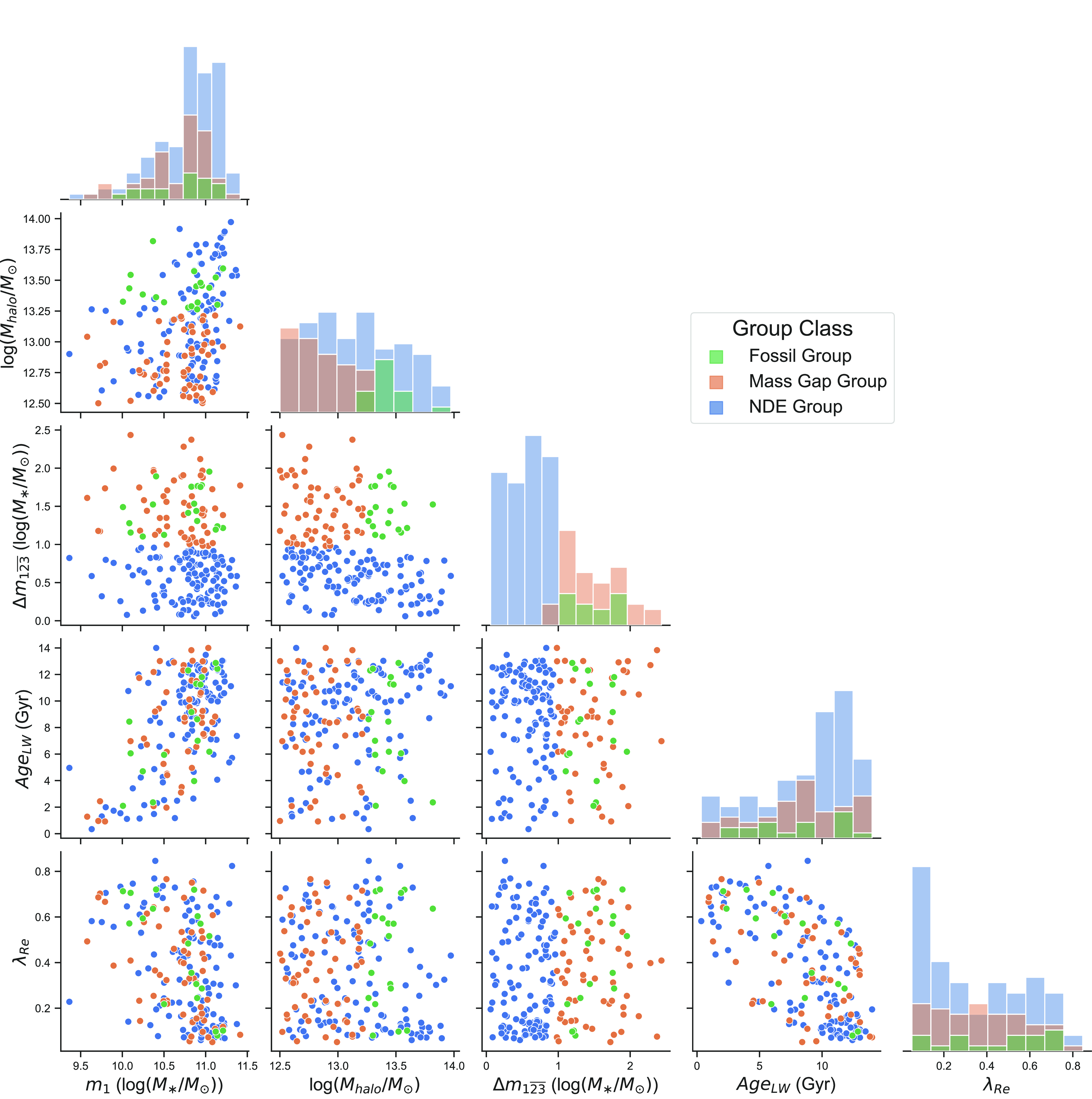
Figure 2. Relationships between key quantities, colour coded by group class, for our SAMI sample. Our selection criteria for group classification can be seen in the mass gap-halo mass plane. The central galaxies of dynamically evolved groups are fairly evenly distributed in
![]() $\lambda_{Re}$
and light-weighted age. Conversely, central galaxies of the NDEGs appear more likely to have a lower spin and older age.
$\lambda_{Re}$
and light-weighted age. Conversely, central galaxies of the NDEGs appear more likely to have a lower spin and older age.
Table 1 also includes the incidences for the three group classes in our EAGLE and Magneticum samples. We consider the fraction of groups in each group class as it is more robust than number density, which is very sensitive to halo mass cut. We find similar fractions of FGs in both SAMI and EAGLE, but a lower fraction in Magneticum. MGGs (in lower mass haloes) are fractionally more common than FGs (in higher mass haloes) for both SAMI and EAGLE. The prevalence of MGGs in SAMI is slightly lower than in EAGLE, and substantially higher than in Magneticum. Indeed, our Magneticum sample consists predominantly of groups that are not dynamically evolved.
It is difficult to compare incidence rates for fossil groups and mass gap groups across studies. This is largely due to differences in both the halo mass range considered and the satellite search radius adopted around the group central. Notwithstanding, a comparison of the literature is presented by (Dariush et al. Reference Dariush2007, Table 1), which shows incidences broadly in line with our findings.
4.2. Group Class trends in SAMI
Fig. 2 reveals a number of general group class similarities and differences in our SAMI sample. First, the central galaxies of dynamically evolved groups (DEGs, i.e. FGs and MGGs) are fairly uniformly distributed in
![]() $\lambda_{Re}$
and age. In contrast, centrals of NDEGs tend to be older (two-sample K-S test
$\lambda_{Re}$
and age. In contrast, centrals of NDEGs tend to be older (two-sample K-S test
![]() $p_{K-S} = 0.031$
) and are overrepresented at very low spin (albeit not statistically significant:
$p_{K-S} = 0.031$
) and are overrepresented at very low spin (albeit not statistically significant:
![]() $p_{K-S} = 0.172$
). This may be driven by the fact that the NDEGs have slightly higher mass, which is why we employ mass matching in our subsequent analysis. Second, NDEGs are distributed across the
$p_{K-S} = 0.172$
). This may be driven by the fact that the NDEGs have slightly higher mass, which is why we employ mass matching in our subsequent analysis. Second, NDEGs are distributed across the
![]() $12.5 \unicode{x003C}$
log
$12.5 \unicode{x003C}$
log
![]() $(M_{halo}/M_{\odot}) \unicode{x003C} 14$
halo mass range considered in our investigation, whereas DEGs are distributed up to log
$(M_{halo}/M_{\odot}) \unicode{x003C} 14$
halo mass range considered in our investigation, whereas DEGs are distributed up to log
![]() $(M_{halo}/M_{\odot}) \approx 13.5$
, beyond which we detect next to none (
$(M_{halo}/M_{\odot}) \approx 13.5$
, beyond which we detect next to none (
![]() $p_{K-S} = 0.074$
). Finally, we find that there are far fewer DEG centrals with log
$p_{K-S} = 0.074$
). Finally, we find that there are far fewer DEG centrals with log
![]() $(M_{\ast}/M_{\odot}) \gtrsim 11$
relative to NDEG centrals (
$(M_{\ast}/M_{\odot}) \gtrsim 11$
relative to NDEG centrals (
![]() $p_{K-S} = 0.012$
).
$p_{K-S} = 0.012$
).
4.3.
 $\lambda_{\boldsymbol{Re}}$
and
$\lambda_{\boldsymbol{Re}}$
and
 $\boldsymbol{f}_{\boldsymbol{SR}}$
$\boldsymbol{f}_{\boldsymbol{SR}}$
Our results comparing the galaxy spin of centrals in FGs, MGGs, and NDEGs, in our observational and simulational data, are presented in Fig. 3. In Fig. 3a, b, and c we bin by halo mass in the following three bins:
![]() $12.5 \unicode{x003C} \text{log}(M_{halo}/M_{\odot}) \unicode{x003C} 12.875$
,
$12.5 \unicode{x003C} \text{log}(M_{halo}/M_{\odot}) \unicode{x003C} 12.875$
,
![]() $12.875 \unicode{x003C} \text{log}(M_{halo}/M_{\odot}) \unicode{x003C} 13.25$
, and
$12.875 \unicode{x003C} \text{log}(M_{halo}/M_{\odot}) \unicode{x003C} 13.25$
, and
![]() $13.25 \unicode{x003C} \text{log}(M_{halo}/M_{\odot}) \unicode{x003C} 14$
. Data in Fig. 3d, e, and f have been binned by the stellar mass of the group central in three bins:
$13.25 \unicode{x003C} \text{log}(M_{halo}/M_{\odot}) \unicode{x003C} 14$
. Data in Fig. 3d, e, and f have been binned by the stellar mass of the group central in three bins:
![]() $10 \unicode{x003C} \text{log}(M_{\ast}/M_{\odot}) \unicode{x003C} 10.6$
,
$10 \unicode{x003C} \text{log}(M_{\ast}/M_{\odot}) \unicode{x003C} 10.6$
,
![]() $10.6 \unicode{x003C} \text{log}(M_{\ast}/M_{\odot}) \unicode{x003C} 11.2$
, and
$10.6 \unicode{x003C} \text{log}(M_{\ast}/M_{\odot}) \unicode{x003C} 11.2$
, and
![]() $11.2 \unicode{x003C} \text{log}(M_{halo}/M_{\odot}) \unicode{x003C} 11.8$
.
$11.2 \unicode{x003C} \text{log}(M_{halo}/M_{\odot}) \unicode{x003C} 11.8$
.

Figure 3. Group centrals in our SAMI (a, d), EAGLE (b, e), and Magneticum (c, f) data in the spin-halo mass (a, b, c) and spin-stellar mass (d, e, f) planes. In simulations, we see clear separation between the spins of DEG and NDEG centrals, supporting the idea that merging drives down
![]() $\lambda_{Re}$
. In contrast, we find no significant difference for spin in SAMI between MGG and NDEG centrals, and we find that FG centrals have typically higher spins than NDEG centrals. Our SAMI results suggest that the mergers that form fossil groups are not the types of mergers that spin down galaxies and form SR. Unfilled points do not have well-defined bootstrapping uncertainties as they contain only a single galaxy.
$\lambda_{Re}$
. In contrast, we find no significant difference for spin in SAMI between MGG and NDEG centrals, and we find that FG centrals have typically higher spins than NDEG centrals. Our SAMI results suggest that the mergers that form fossil groups are not the types of mergers that spin down galaxies and form SR. Unfilled points do not have well-defined bootstrapping uncertainties as they contain only a single galaxy.
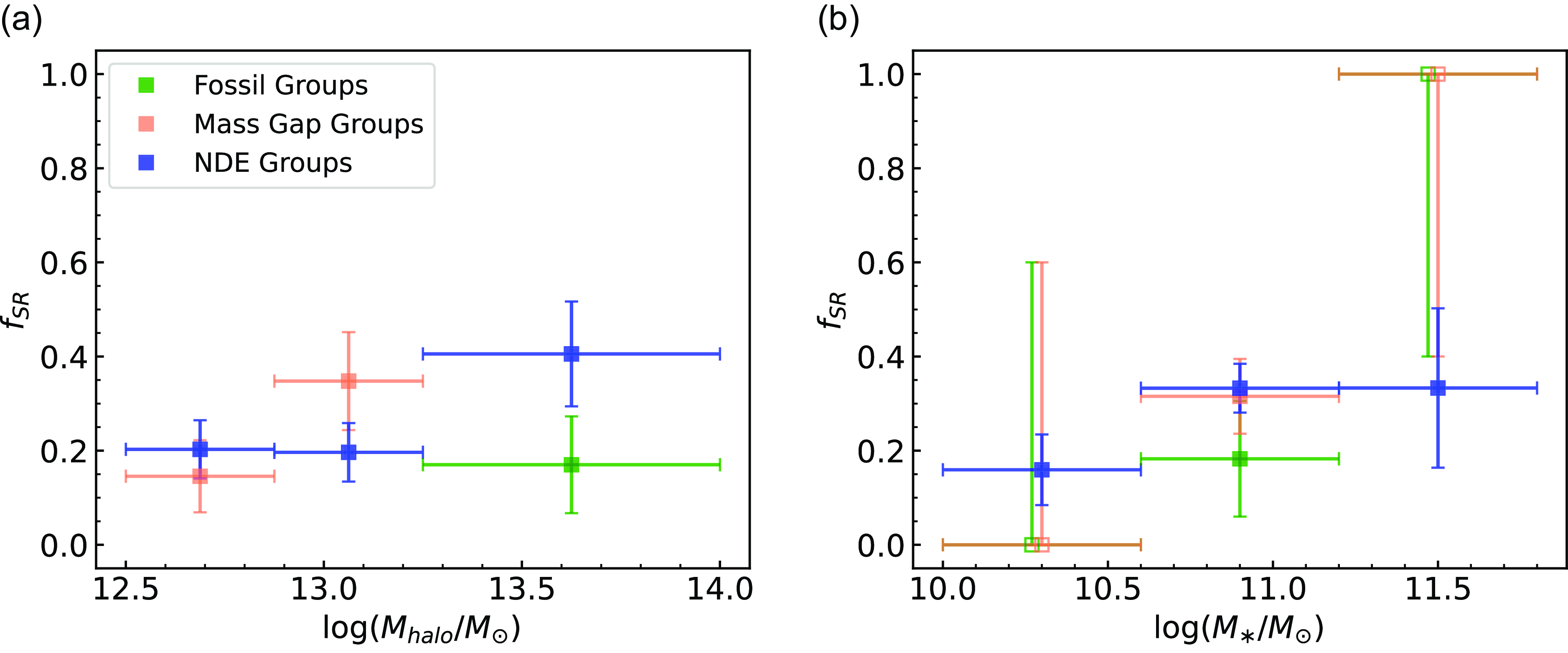
Figure 4. Our SAMI data in the fraction of slow rotators (
![]() $f_{SR}$
)-halo mass (a) and
$f_{SR}$
)-halo mass (a) and
![]() $f_{SR}$
-stellar mass (b) planes. At fixed halo and stellar mass, FG centrals appear less likely to be slow rotators than NDEG centrals. These results directly follow from our findings in Fig. 3a and d given the slow rotator selection criteria we adopt (see Section 3.2). For unfilled points we report binomial uncertainties containing the 68% confidence regions, as they contain only a single galaxy.
$f_{SR}$
-stellar mass (b) planes. At fixed halo and stellar mass, FG centrals appear less likely to be slow rotators than NDEG centrals. These results directly follow from our findings in Fig. 3a and d given the slow rotator selection criteria we adopt (see Section 3.2). For unfilled points we report binomial uncertainties containing the 68% confidence regions, as they contain only a single galaxy.
As discussed in Section 3.3, we emphasise the importance of controlling for stellar mass when comparing
![]() $\lambda_{Re}$
between galaxies. When binning by halo mass, this was achieved by stellar mass matching unique DEG/NDEG central pairs in each bin to within
$\lambda_{Re}$
between galaxies. When binning by halo mass, this was achieved by stellar mass matching unique DEG/NDEG central pairs in each bin to within
![]() $0.15 \text{log}(M_{halo}/M_{\odot})$
. We do not employ this mass matching techinique when binning by stellar mass i.e. Fig. 3d, e, and f. Error bars indicate uncertainty on the mean at the
$0.15 \text{log}(M_{halo}/M_{\odot})$
. We do not employ this mass matching techinique when binning by stellar mass i.e. Fig. 3d, e, and f. Error bars indicate uncertainty on the mean at the
![]() $1 \sigma$
level and are calculated using bootstrapping (see Section 3.3).
$1 \sigma$
level and are calculated using bootstrapping (see Section 3.3).
In SAMI, we find that for a given halo mass bin, the spins of NDEG centrals are comparable to those of MGG centrals. On the other hand, the spins of FG centrals are, on average, slightly higher (albeit not significantly) than their NDEG counterparts (Fig. 3a). Fig. 3d reveals that these higher
![]() $\lambda_{Re}$
FG centrals have a low or intermediate stellar mass. We find a similar result for
$\lambda_{Re}$
FG centrals have a low or intermediate stellar mass. We find a similar result for
![]() $f_{SR}$
(Fig. 4), that is, fossil group centrals are less likely to be SRs than NDEG centrals, driven by a population of fast rotator FG centrals in the low and intermediate stellar mass range. This is perhaps unsurprising given that the slow rotator selection criteria depends primarily on
$f_{SR}$
(Fig. 4), that is, fossil group centrals are less likely to be SRs than NDEG centrals, driven by a population of fast rotator FG centrals in the low and intermediate stellar mass range. This is perhaps unsurprising given that the slow rotator selection criteria depends primarily on
![]() $\lambda_{Re}$
. To be thorough, we repeated our analysis of
$\lambda_{Re}$
. To be thorough, we repeated our analysis of
![]() $f_{SR}$
using the other SR selection criteria stated in Section 3.2. We still found that FG centrals were slightly less likely to be SRs than NDEGs, however the difference seen in Fig. 4a between these two group classes was no longer significant.
$f_{SR}$
using the other SR selection criteria stated in Section 3.2. We still found that FG centrals were slightly less likely to be SRs than NDEGs, however the difference seen in Fig. 4a between these two group classes was no longer significant.
These results for fossil group centrals are inconsistent with the current understanding of SRs. We know from simulations (e.g. Lagos et al. Reference Lagos2022; Valenzuela & Remus Reference Valenzuela and Remus2022) as well as growing observational evidence (e.g. Rutherford et al. Reference Rutherford2024) that mergers play a key role in the formation of slow rotators, and that fossil group centrals are thought to typically undergo more mergers than non-FG centrals (Kundert et al. Reference Kundert, D’Onghia and Aguerri2017). Hence we would expect FG centrals to have a lower spin, on average, and be more likely to be SRs, than non-FG centrals. Our findings, however, suggest that the types of mergers that form fossil groups are not the types of mergers that form SRs.
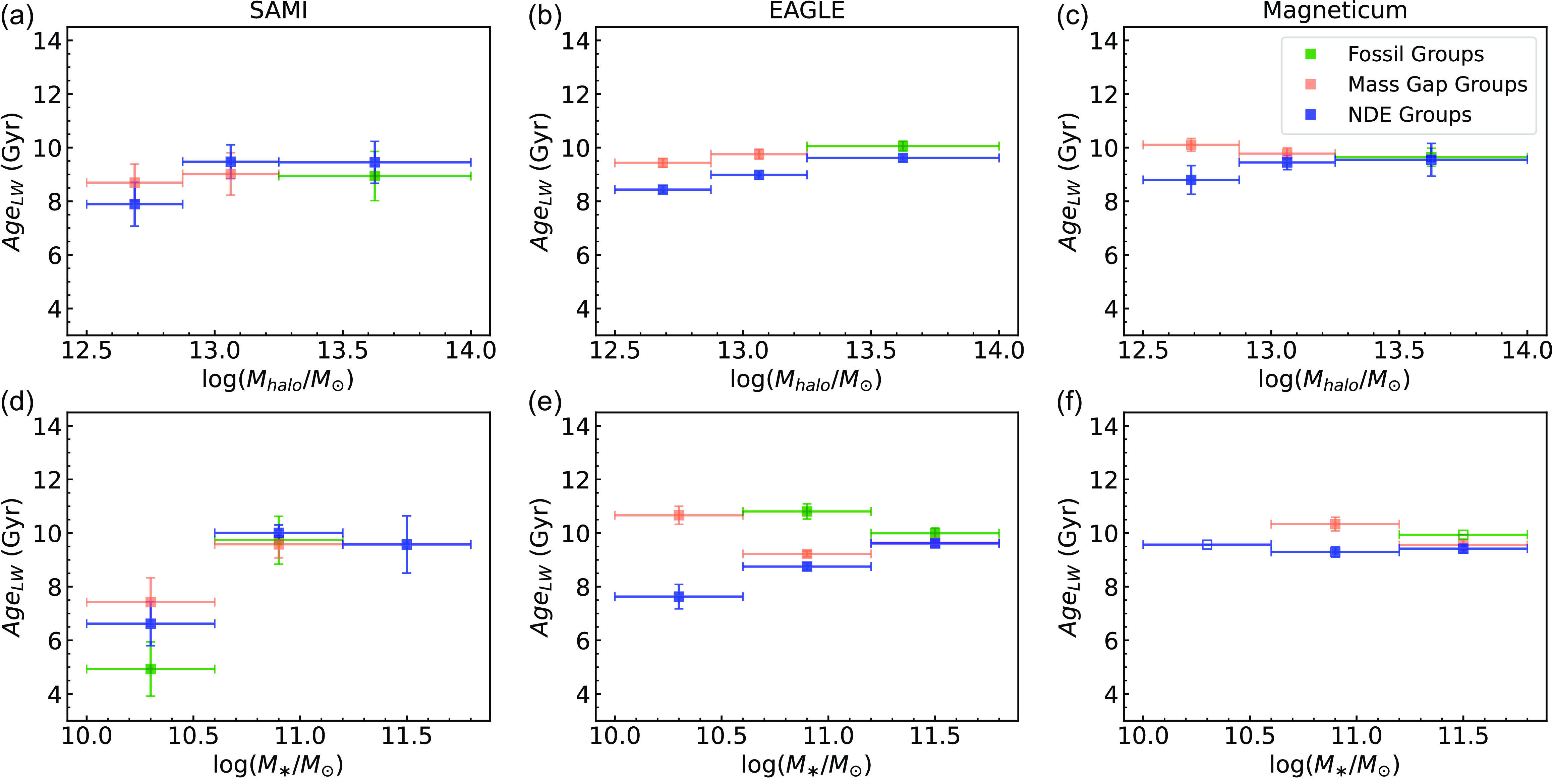
Figure 5. Similar to Fig. 3, but for light-weighted age,
![]() $Age_{LW}$
. In SAMI, we detect no significant difference in
$Age_{LW}$
. In SAMI, we detect no significant difference in
![]() $Age_{LW}$
between DEG and NDEG centrals, except for a population of relatively younger, low mass FG centrals. In simulations, we detect a significant difference in age between NDEG and DEG centrals, in the low and intermediate halo and stellar mass bins.
$Age_{LW}$
between DEG and NDEG centrals, except for a population of relatively younger, low mass FG centrals. In simulations, we detect a significant difference in age between NDEG and DEG centrals, in the low and intermediate halo and stellar mass bins.
In contrast, our
![]() $\lambda_{Re}$
findings in EAGLE (Fig. 3b and e) and Magneticum (Fig. 3c and f) are in agreement with the current picture of slow rotator formation. Our results in simulations suggest that, at fixed halo/stellar mass, centrals in groups with a high mass gap (
$\lambda_{Re}$
findings in EAGLE (Fig. 3b and e) and Magneticum (Fig. 3c and f) are in agreement with the current picture of slow rotator formation. Our results in simulations suggest that, at fixed halo/stellar mass, centrals in groups with a high mass gap (
![]() $\Delta m_{1\bar{23}} \gtrsim 1$
) tend to have a lower spin than centrals in low mass gap (
$\Delta m_{1\bar{23}} \gtrsim 1$
) tend to have a lower spin than centrals in low mass gap (
![]() $\Delta m_{1\bar{23}} \lesssim 1$
) groups. In most cases the difference in
$\Delta m_{1\bar{23}} \lesssim 1$
) groups. In most cases the difference in
![]() $\lambda_{Re}$
in the simulations is striking: we detect a difference well beyond the
$\lambda_{Re}$
in the simulations is striking: we detect a difference well beyond the
![]() $1\sigma$
level.
$1\sigma$
level.
4.4. Light-weighted age
There is an emerging picture that
![]() $\lambda_{Re}$
is most strongly correlated with age (van de Sande et al. Reference van de Sande2018; Croom et al. Reference Croom2024), that is, the spin of a galaxy decreases as the stellar population gets older. For instance, Croom et al. (Reference Croom2024) perform a partial correlation analysis and find that age is much more important than mass and environment in determining spin. This relationship is evident in the
$\lambda_{Re}$
is most strongly correlated with age (van de Sande et al. Reference van de Sande2018; Croom et al. Reference Croom2024), that is, the spin of a galaxy decreases as the stellar population gets older. For instance, Croom et al. (Reference Croom2024) perform a partial correlation analysis and find that age is much more important than mass and environment in determining spin. This relationship is evident in the
![]() $\lambda_{Re}-Age_{LW}$
plane of Fig. 2.
$\lambda_{Re}-Age_{LW}$
plane of Fig. 2.
We therefore perform an identical analysis for light-weighted age as for
![]() $\lambda_{Re}$
, presented in Fig. 5. We use light-weighted age instead of mass-weighted age as spin is most likely related to when the galaxy is quenched (e.g. Lagos et al. Reference Lagos2018; Lagos et al. Reference Lagos2022), making light-weighted age a better proxy for time since the significant star formation. In SAMI, for any given halo mass bin, we find no significant difference in age between DEG and NDEG centrals (Fig. 5a). When binning by stellar mass (Fig. 5d), however, we identify a population of low mass FG centrals that are generally younger than low mass MGG and NDEG centrals. We do not see a similar younger population of FG centrals in the intermediate and high mass bins. The same qualitative result is found when we repeat the analysis with mass weighted ages (not shown).
$\lambda_{Re}$
, presented in Fig. 5. We use light-weighted age instead of mass-weighted age as spin is most likely related to when the galaxy is quenched (e.g. Lagos et al. Reference Lagos2018; Lagos et al. Reference Lagos2022), making light-weighted age a better proxy for time since the significant star formation. In SAMI, for any given halo mass bin, we find no significant difference in age between DEG and NDEG centrals (Fig. 5a). When binning by stellar mass (Fig. 5d), however, we identify a population of low mass FG centrals that are generally younger than low mass MGG and NDEG centrals. We do not see a similar younger population of FG centrals in the intermediate and high mass bins. The same qualitative result is found when we repeat the analysis with mass weighted ages (not shown).
In EAGLE and Magneticum, we detect a significant difference in age between DEG and NDEG centrals, that is, DEG centrals tend to be older than NDEG centrals, in the low stellar mass and low halo mass regimes. This age gap generally decreases as we move to the intermediate bins, and is non-existent in the high stellar halo mass bins. Unlike in SAMI, we do not see a younger population of low mass FG centrals in simulations.
5. Discussion
In SAMI, we find no difference in spin between FG centrals and NDEG centrals. Our observational results therefore suggest that the properties of mergers that spin down galaxies and form SRs are not the properties of mergers that form fossil groups. In contrast, our findings in EAGLE and Magneticum strongly suggest that MGG and FG centrals have lower spins than NDEG centrals. We note that some small fraction of fossil groups may form with lower spins without the result of mergers, as is the case with SR formation Lagos et al. (Reference Lagos2022). We will now discuss and provide possible explanations for these results.
5.1. Merger properties
Differences between the properties of mergers that are required to reduce galaxy spin and form a slow rotator, and the mergers that form fossil groups, may explain the
![]() $\lambda_{Re}$
and
$\lambda_{Re}$
and
![]() $f_{SR}$
discrepancies that we have found in SAMI. There is strong evidence from simulations that merger progenitors need to be gas-poor or quenched, otherwise the gas will eventually reform a disk and hence spin-up the merger remnant (e.g. Hoffman et al. Reference Hoffman, Cox, Dutta and Hernquist2010; Naab et al. Reference Naab2014; Lagos et al. Reference Lagos2018; Lagos et al. Reference Lagos2022). Major merging tends to produce SRs with larger ellipticities (Khochfar et al. Reference Khochfar2011; Bois et al. Reference Bois2011; Jesseit, Naab, & Burkert Reference Jesseit, Naab and Burkert2005; Schulze et al. Reference Schulze2018) whereas multiple dry minor mergers form most of the round SRs (Moody et al. Reference Moody, Romanowsky, Cox, Novak and Primack2014; Naab et al. Reference Naab2014). Mergers with a small impact parameter, i.e. radial mergers have also been shown to be more effective at randomising stellar orbits and hence producing SRs (Duc et al. Reference Duc2011; Karademir et al. Reference Karademir2019; Schulze et al. Reference Schulze2020).
$f_{SR}$
discrepancies that we have found in SAMI. There is strong evidence from simulations that merger progenitors need to be gas-poor or quenched, otherwise the gas will eventually reform a disk and hence spin-up the merger remnant (e.g. Hoffman et al. Reference Hoffman, Cox, Dutta and Hernquist2010; Naab et al. Reference Naab2014; Lagos et al. Reference Lagos2018; Lagos et al. Reference Lagos2022). Major merging tends to produce SRs with larger ellipticities (Khochfar et al. Reference Khochfar2011; Bois et al. Reference Bois2011; Jesseit, Naab, & Burkert Reference Jesseit, Naab and Burkert2005; Schulze et al. Reference Schulze2018) whereas multiple dry minor mergers form most of the round SRs (Moody et al. Reference Moody, Romanowsky, Cox, Novak and Primack2014; Naab et al. Reference Naab2014). Mergers with a small impact parameter, i.e. radial mergers have also been shown to be more effective at randomising stellar orbits and hence producing SRs (Duc et al. Reference Duc2011; Karademir et al. Reference Karademir2019; Schulze et al. Reference Schulze2020).
In contrast, fossil group formation is essentially unaffected by such merger properties: merging of satellite galaxies with the group central is all that is required. This may explain why we found that fossil group centrals in SAMI were not more likely to be SRs than NDEG centrals. Further, since satellites are typically gas-rich disk galaxies, this might account for our FG centrals having a slightly higher average spin and lower
![]() $f_{SR}$
than NDEG centrals.
$f_{SR}$
than NDEG centrals.
So why do DEG centrals in EAGLE and Magneticum have lower spins than NDEG centrals? We found that DEG centrals are slightly older in simulations (Fig. 5), so one possible explanation is that DEGs are more likely to contain passive galaxies. Another possibility is that the cold gas in satellites is stripped more efficiently by the hot group gas halo in simulations than in reality, which enhances the dry merging with the central galaxy.
5.2. Merger remnants and redshift
Most star formation in galaxies peaked around 10 Gyr ago and has since decreased substantially (Madau & Dickinson Reference Madau and Dickinson2014). Hence, mergers that occur at higher redshifts (
![]() $z \gtrsim 1$
) tend to involve relatively younger galaxies, i.e. galaxies that are less likely to be quenched (Tacconi et al. Reference Tacconi2010). Consequently, some studies have supported the notion that timing is important for reducing
$z \gtrsim 1$
) tend to involve relatively younger galaxies, i.e. galaxies that are less likely to be quenched (Tacconi et al. Reference Tacconi2010). Consequently, some studies have supported the notion that timing is important for reducing
![]() $\lambda_{Re}$
and forming a slow rotator. Bezanson et al. (Reference Bezanson2018) found that quenched galaxies must lose spin in the 0–7 Gyr range. Schulze et al. (Reference Schulze2018) found that most fast-to-slow rotator evolution starts around 8 Gyr ago, although some formation before this time was also predicted in a larger simulation volume at redshifts as high as
$\lambda_{Re}$
and forming a slow rotator. Bezanson et al. (Reference Bezanson2018) found that quenched galaxies must lose spin in the 0–7 Gyr range. Schulze et al. (Reference Schulze2018) found that most fast-to-slow rotator evolution starts around 8 Gyr ago, although some formation before this time was also predicted in a larger simulation volume at redshifts as high as
![]() $z \approx 4$
(Kimmig et al. Reference Kimmig2023). Lagos et al. (Reference Lagos2022) instead found SR formation to preferentially occur around 2–6 Gyr ago. Hence, whilst there is some range in timescales from different studies, most predict that SRs form between 8 Gyr ago and the present.
$z \approx 4$
(Kimmig et al. Reference Kimmig2023). Lagos et al. (Reference Lagos2022) instead found SR formation to preferentially occur around 2–6 Gyr ago. Hence, whilst there is some range in timescales from different studies, most predict that SRs form between 8 Gyr ago and the present.
We therefore expect the remnants of mergers that occurred over 8 Gyr ago to be more likely to remain a rotating disk. Given that our SAMI results suggested that FG centrals are not more likely to be SRs than NDEG centrals, a plausible explanation is that the mergers that form fossil groups happen at higher redshifts. Chu et al. (Reference Chu2023) argue that fossil groups form before, and cease evolving by,
![]() $z\approx1.8$
(10 Gyr ago), supporting this idea. Note that although for some of our observed FG centrals
$z\approx1.8$
(10 Gyr ago), supporting this idea. Note that although for some of our observed FG centrals
![]() $Age_{LW} \approx$
5 Gyr (Fig. 5d), these galaxies may have undergone early merging and then continued to form stars.
$Age_{LW} \approx$
5 Gyr (Fig. 5d), these galaxies may have undergone early merging and then continued to form stars.
5.3. Location in large scale structure
We are now starting to find evidence that some aspects of angular momentum in galaxies are related to large scale structure: the filaments, nodes and voids that make up the cosmic web (Barsanti et al. Reference Barsanti2022). Whilst merging between the group central and satellites is required for a fossil system to form, if the group itself accretes new high mass galaxies – repopulates – then it may no longer be classified as a fossil group. This suggests that fossil groups are more likely to form in the underdense voids of the cosmic web. Indeed, Zarattini et al. (Reference Zarattini, Aguerri, Tarro and Corsini2023) found that fossil groups tend to be more isolated from large scale structure than non-fossil groups.
SRs, on the other hand, may be more likely to form at nodes due to merging from different angles, i.e. along different filaments, having a particularly destructive effect on the remnant’s spin. This possible difference in where SRs and fossil groups tend to form within the cosmic web may explain why we found that fossil group centrals in SAMI are not more likely to be SRs.
There are a couple of reasons as to why this location argument does not appear to hold in simulations. First, when the merging occurs may be more important than where. Second, the box sizes used in EAGLE and Magneticum are perhaps too small to sample large scale structure with statistical significance. Moreover, box size has been shown to impact environment and structure formation (Kimmig et al. Reference Kimmig2023).
5.4. Measuring halo mass
In our investigation we identified a population of low mass fossil group centrals in SAMI with a relatively higher
![]() $\lambda_{Re}$
and lower
$\lambda_{Re}$
and lower
![]() $Age_{LW}$
than low mass NDEG centrals. Specifically, these FG centrals have a stellar mass between
$Age_{LW}$
than low mass NDEG centrals. Specifically, these FG centrals have a stellar mass between
![]() $10^{10}$
and
$10^{10}$
and
![]() $10^{10.6} M_{\odot}$
, and a halo mass above
$10^{10.6} M_{\odot}$
, and a halo mass above
![]() $10^{13.25} M_{\odot}$
, which is rather unusual. These galaxies lie in the bottom-right region of Fig. 1, far away from the tight log
$10^{13.25} M_{\odot}$
, which is rather unusual. These galaxies lie in the bottom-right region of Fig. 1, far away from the tight log
![]() $(M_{\ast}/M_{\odot}) - \text{log}(M_{halo}/M_{\odot})$
relation seen in simulations. This suggests significant uncertainty in our halo mass measurements for fossil groups.
$(M_{\ast}/M_{\odot}) - \text{log}(M_{halo}/M_{\odot})$
relation seen in simulations. This suggests significant uncertainty in our halo mass measurements for fossil groups.
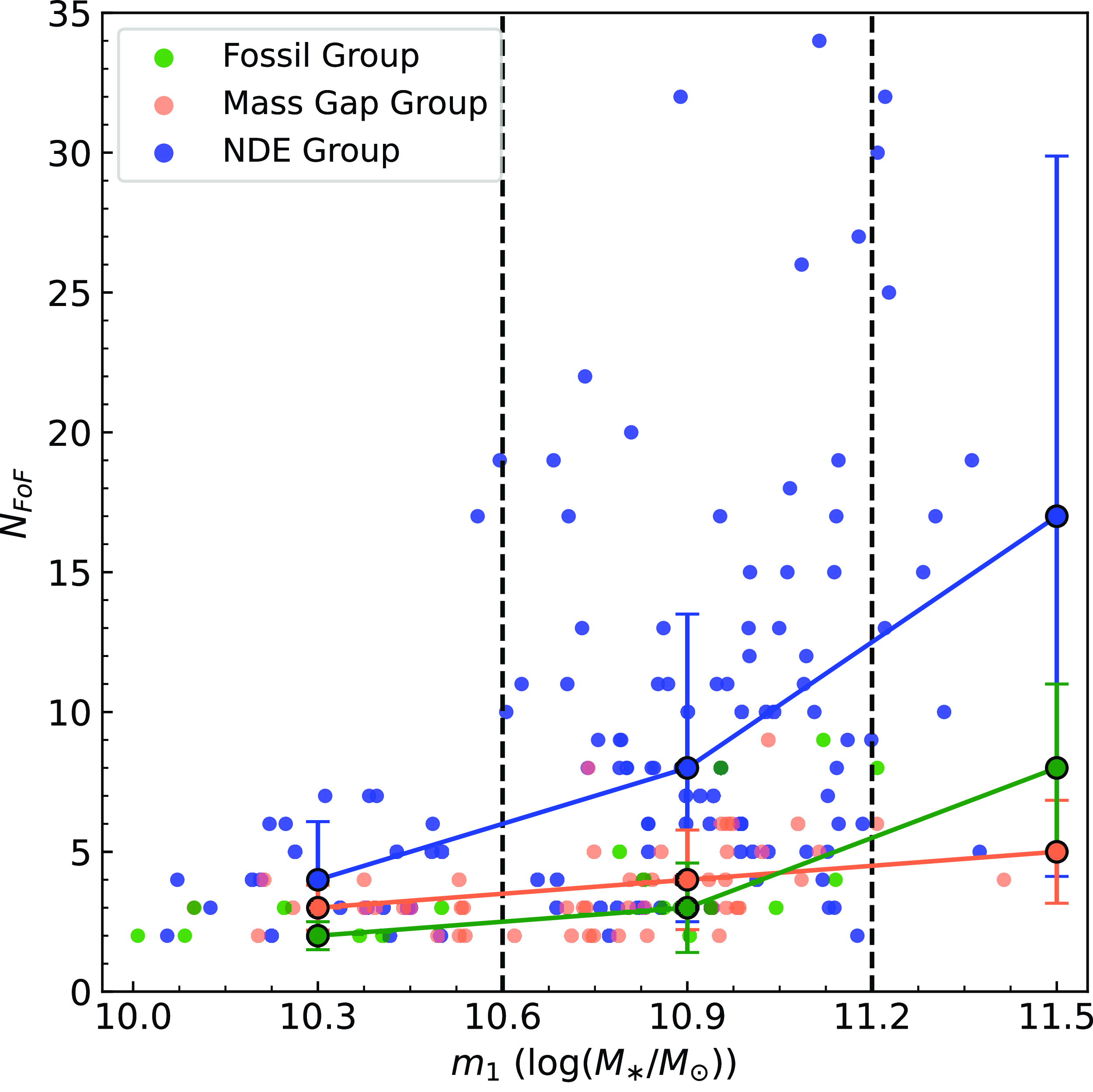
Figure 6. Group multiplicity (
![]() $N_{FoF}$
) vs. central mass in our SAMI sample. Larger points are the median
$N_{FoF}$
) vs. central mass in our SAMI sample. Larger points are the median
![]() $N_{FoF}$
of each stellar mass bin used in our investigation (delineated by dashed lines), with uncertainties as 68% confidence intervals. DEGs have very few group members in the low and intermediate mass ranges, making it difficult to estimate their halo mass. This is affecting our ability to distinguish between MGGs and FGs, adding noise.
$N_{FoF}$
of each stellar mass bin used in our investigation (delineated by dashed lines), with uncertainties as 68% confidence intervals. DEGs have very few group members in the low and intermediate mass ranges, making it difficult to estimate their halo mass. This is affecting our ability to distinguish between MGGs and FGs, adding noise.
Our halo mass measurements for SAMI centrals were taken from GAMA, which were estimated by Robotham et al. (Reference Robotham2011) using the following relation:
![]() $M_{halo} = A \sigma^2R$
, where
$M_{halo} = A \sigma^2R$
, where
![]() $\sigma$
is the group velocity dispersion, R is the radius containing 50% of the group’s members, and
$\sigma$
is the group velocity dispersion, R is the radius containing 50% of the group’s members, and
![]() $A=10.0$
is a simulation-calibrated proportionality constant. We make the assumption that the halo mass of fossil groups follows the mean relation. There is a strong relationship between the shape of the halo mass probability density function and group multiplicity, since a greater number of galaxies yields more accurate estimates for R and especially
$A=10.0$
is a simulation-calibrated proportionality constant. We make the assumption that the halo mass of fossil groups follows the mean relation. There is a strong relationship between the shape of the halo mass probability density function and group multiplicity, since a greater number of galaxies yields more accurate estimates for R and especially
![]() $\sigma$
. Robotham et al. (Reference Robotham2011) find that bias is small for
$\sigma$
. Robotham et al. (Reference Robotham2011) find that bias is small for
![]() $N_{FoF} \geq 5$
, however, for
$N_{FoF} \geq 5$
, however, for
![]() $N_{FoF} \leq 4$
, the recovered distribution is not as tight and symmetrical (see Fig. 6 in Robotham et al. Reference Robotham2011).
$N_{FoF} \leq 4$
, the recovered distribution is not as tight and symmetrical (see Fig. 6 in Robotham et al. Reference Robotham2011).
Fig. 6 shows our SAMI sample in the
![]() $N_{FoF}-m_1$
plane, including the median (larger points) and 68% confidence interval of each stellar mass bin (demarcated by dashed lines). The group multiplicities of our dynamically evolved groups are in agreement with the literature (e.g. Jones et al. Reference Jones2003; Dariush et al. Reference Dariush2007), and are particularly low in the low and intermediate mass bins. Since FG and MGG classification differ only in halo mass, it is likely that our FG sample is being contaminated with MGGs, especially in the low mass bin, and that our MGG sample is being contaminated with FGs, particularly in the intermediate and high mass bins. This contamination may explain why we see an anomalous sub-population of low mass fossil group centrals, which is increasing the average spin and decreasing the average
$N_{FoF}-m_1$
plane, including the median (larger points) and 68% confidence interval of each stellar mass bin (demarcated by dashed lines). The group multiplicities of our dynamically evolved groups are in agreement with the literature (e.g. Jones et al. Reference Jones2003; Dariush et al. Reference Dariush2007), and are particularly low in the low and intermediate mass bins. Since FG and MGG classification differ only in halo mass, it is likely that our FG sample is being contaminated with MGGs, especially in the low mass bin, and that our MGG sample is being contaminated with FGs, particularly in the intermediate and high mass bins. This contamination may explain why we see an anomalous sub-population of low mass fossil group centrals, which is increasing the average spin and decreasing the average
![]() $f_{SR}$
of the general FG population.
$f_{SR}$
of the general FG population.
6. Conclusion
We have compared the spin parameter proxy
![]() $\lambda_{Re}$
, light-weighted age (
$\lambda_{Re}$
, light-weighted age (
![]() $Age_{LW}$
), and
$Age_{LW}$
), and
![]() $f_{SR}$
of SAMI Galaxy Survey centrals in groups at three different stages of dynamical evolution: not dynamically evolved (NDEGs), mass gap groups (MGGs), and fossil groups (FGs). We used a combination of mass gap and halo mass to classify SAMI centrals into our three group classes. We controlled for stellar mass throughout our investigation. We also repeated our analysis on samples from the EAGLE and Magneticum simulations, in the same halo mass range as for SAMI.
$f_{SR}$
of SAMI Galaxy Survey centrals in groups at three different stages of dynamical evolution: not dynamically evolved (NDEGs), mass gap groups (MGGs), and fossil groups (FGs). We used a combination of mass gap and halo mass to classify SAMI centrals into our three group classes. We controlled for stellar mass throughout our investigation. We also repeated our analysis on samples from the EAGLE and Magneticum simulations, in the same halo mass range as for SAMI.
We find a clear
![]() $\lambda_{Re}$
trend in simulations where MGG and FG centrals have lower spins, on average, than NDEG centrals. This trend persists whether we bin by halo mass or stellar mass. Given that FGs and MGGs typically undergo more merging than NDEGs, these findings support the current picture that merging randomises stellar orbits and hence reduces galaxy spin.
$\lambda_{Re}$
trend in simulations where MGG and FG centrals have lower spins, on average, than NDEG centrals. This trend persists whether we bin by halo mass or stellar mass. Given that FGs and MGGs typically undergo more merging than NDEGs, these findings support the current picture that merging randomises stellar orbits and hence reduces galaxy spin.
In contrast, we do not see this trend in our SAMI sample. On average, SAMI FG centrals in the low and intermediate stellar mass range are found to have slightly higher spins than their NDEG central counterparts. Consequently, we find that SAMI FG centrals have a lower
![]() $f_{SR}$
than SAMI NDEG centrals. These results suggest that the types of mergers that form the vast majority of fossil groups are not the types of mergers that form SRs.
$f_{SR}$
than SAMI NDEG centrals. These results suggest that the types of mergers that form the vast majority of fossil groups are not the types of mergers that form SRs.
Indeed, whilst slow rotator formation is necessarily a product of gas-poor or quenched progenitors, fossil group formation only requires satellite-central merging. Further, there is evidence to suggest that SRs generally form later than FGs (
![]() $\lesssim8$
Gyr ago vs.
$\lesssim8$
Gyr ago vs.
![]() $\approx10$
Gyr ago, respectively). SRs and FGs may also preferentially form in different locations in large scale structure: SRs at nodes to more effectively reduce angular momentum and FGs in voids to avoid becoming repopulated. Finally, we suspect uncertainty in halo mass measurements to be introducing significant noise to MGGs and FGs in our SAMI sample.
$\approx10$
Gyr ago, respectively). SRs and FGs may also preferentially form in different locations in large scale structure: SRs at nodes to more effectively reduce angular momentum and FGs in voids to avoid becoming repopulated. Finally, we suspect uncertainty in halo mass measurements to be introducing significant noise to MGGs and FGs in our SAMI sample.
For
![]() $Age_{LW}$
, we detected a population of relatively younger low mass FG centrals in SAMI that was not present in our EAGLE and Magneticum data. We otherwise found no significant difference in age between DEG and NDEG centrals in SAMI. Conversely, in simulations, DEG centrals were generally slightly older than NDEG centrals, in the low and intermediate stellar and halo mass regimes.
$Age_{LW}$
, we detected a population of relatively younger low mass FG centrals in SAMI that was not present in our EAGLE and Magneticum data. We otherwise found no significant difference in age between DEG and NDEG centrals in SAMI. Conversely, in simulations, DEG centrals were generally slightly older than NDEG centrals, in the low and intermediate stellar and halo mass regimes.
The Hector galaxy survey (Bryant et al. Reference Bryant2020) – the successor of SAMI – will provide a larger data set (roughly
![]() $5\times$
larger) to better understand the relationship between dynamically evolved groups and SRs. Additionally, the full eROSITA All-Sky Survey (Predehl et al. Reference Predehl2021) will provide X-ray data needed to more reliably identify fossil groups, and also enable the identification of isolated fossil groups where all of the satellites have merged with the central. Finally, higher redshift stellar kinematic data, which could be obtained with the James Webb Space Telescope NIRSpec instrument (Gardner et al. Reference Gardner2006), would shed more light on when SRs form.
$5\times$
larger) to better understand the relationship between dynamically evolved groups and SRs. Additionally, the full eROSITA All-Sky Survey (Predehl et al. Reference Predehl2021) will provide X-ray data needed to more reliably identify fossil groups, and also enable the identification of isolated fossil groups where all of the satellites have merged with the central. Finally, higher redshift stellar kinematic data, which could be obtained with the James Webb Space Telescope NIRSpec instrument (Gardner et al. Reference Gardner2006), would shed more light on when SRs form.
Acknowledgement
The SAMI Galaxy Survey is based on observations made at the Anglo-Australian Telescope. The Sydney-AAO Multi-object Integral field spectrograph (SAMI) was developed jointly by the University of Sydney and the Australian Astronomical Observatory. The SAMI input catalogue is based on data taken from the Sloan Digital Sky Survey, the GAMA Survey and the VST ATLAS Survey. The SAMI Galaxy Survey is supported by the Australian Research Council Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013, the Australian Research Council Centre of Excellence for All-sky Astrophysics (CAASTRO), through project number CE110001020, and other participating institutions. The SAMI Galaxy Survey website is http://sami-survey.org/.
GAMA is a joint European-Australasian project based around a spectroscopic campaign using the Anglo-Australian Telescope. The GAMA input catalogue is based on data taken from the Sloan Digital Sky Survey and the UKIRT Infrared Deep Sky Survey. Complementary imaging of the GAMA regions is being obtained by a number of independent survey programmes including GALEX MIS, VST KiDS, VISTA VIKING, WISE, Herschel-ATLAS, GMRT and ASKAP providing UV to radio coverage. GAMA is funded by the STFC (UK), the ARC (Australia), the AAO, and the participating institutions. The GAMA website is https://www.gama-survey.org/.
The Magneticum simulations were performed at the Leibniz-Rechenzentrum with CPU time assigned to the Project pr83li.
Funding statement
Part of this research was conducted by the Australian Research Council Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013. JJB acknowledges support of an Australian Research Council Future Fellowship (FT180100231). AR acknowledges the receipt of a Scholarship for International Research Fees (SIRF) and an International Living Allowance Scholarship (Ad Hoc Postgraduate Scholarship) at The University of Western Australia. SMS acknowledges funding from the Australian Research Council (DE220100003). LCK acknowledges support by the DFG project nr. 516355818.
Competing interests
None.
Data availability statement
Data used in this investigation are available upon reasonable request. See Section 2 for accessing publicly available GAMA, SAMI, EAGLE, and Magneticum data.