1 INTRODUCTION
In the standard external shock model of Gamma Ray Bursts (GRBs) the afterglow emission is produced when the ultra relativistic jet is decelerated by the interstellar medium (Meszaros & Rees Reference Meszaros and Rees1997). During this phase the bulk Lorentz factor Γ decreases with time while the beaming angle of the emitted radiation Ω(t)∝1/Γ(t)2 increases. Moreover, there is a large consensus both for theoretical and observational reasons, that GRBs are jetted sources. The estimate of the jet opening angle can be derived from the time of the afterglow light curve steepening (the jet break time t break) due to the Lorentz factor becoming ~ 1/θjet (Rhoads et al. Reference Rhoads1997). Typical jet opening angles derived from the afterglow light curve breaks (Frail et al. Reference Frail2001; Ghirlanda et al. Reference Ghirlanda, Ghisellini and Lazzati2004) are clustered around θjet = 0.05 radiants.
Therefore, a GRB which is observed off–axis, with a viewing angle θview>θjet, will be undetected as a prompt burst of γ–ray photons because the prompt emission, produced by material moving with a bulk Lorentz factor Γ0 ~ 102 − 103, is beamed within an angle 1/Γ0 < θjet. However, the afterglow emission (in the optical/NIR and radio band) can be detected when the beaming angle of the radiation intercepts the line of sight, i.e. 1/Γ ~ θview. After this time the emission for an off-axis observer is the same that would be seen if θview < θjet.
Orphan Afterglows (OA) are GRBs seen off-axis detectable at any frequency, without the high energy γ–ray counterpart. For this reason their study follows a different path than normal GRBs (where it is the high energy trigger to initiate a follow up campaign to monitor the afterglow emission at different frequencies). OAs can be detected as transients through wide field deep surveys and they could be a considerable fraction of the population of detected transients (Rohads Reference Rhoads1997, Reference Rhoads2003; Nakar, Piran, & Granot Reference Nakar, Piran and Granot2002; Totani & Panaitescu Reference Totani and Panaitescu2002). Considering the typical jet opening angles measured in GRBs (e.g. Frail et al. Reference Frail2001; Ghirlanda et al. Reference Ghirlanda, Nava, Ghisellini and Firmani2007) θjet ~ 3°, for each GRB detected in the γ–ray band there should be ~ 730 (i.e. ~ 2/θjet 2) bursts pointing in any other direction. These are orphan afterglows.
Upper limits θjet
![]() $\lower.75ex\hbox{$\,\sim $} \llap{\raise.27ex \hbox{$<$}}\,$
22° (Levinson et al. Reference Levinson, Ofek, Waxman and Gal-Yam2002) or lower limits θjet
$\lower.75ex\hbox{$\,\sim $} \llap{\raise.27ex \hbox{$<$}}\,$
22° (Levinson et al. Reference Levinson, Ofek, Waxman and Gal-Yam2002) or lower limits θjet
![]() $\lower.75ex \hbox{$\sim $} \llap{\raise.27ex \hbox{$>$}}\,$
0.8° (Soderberg et al. Reference Soderberg, Nakar and Berger2006) on the typical opening angle of GRBs were inferred from OA searches. However, to date no orphan afterglow has been confirmed. Some transients have been identified as possible OA candidates through archival searches both at radio frequencies (e.g. see Murphy et al. Reference Murphy2012; Bell et al. Reference Bell2011 for a summary of radio OA search results) and in the optical band (e.g. Rau, Greiner, & Schwarz Reference Rau, Greiner and Schwarz2006; Malacrino et al. Reference Malacrino2007; Zou, Wu, & Dai Reference Zou, Wu and Dai2007) but none of these has been confirmed as an orphan GRB afterglow. Even the very recent discovery (Cenko et al. Reference Cenko2013) of an optical transient by the Palomar Transient Survey (PTF) seems favour a “dirty fireball” or an untriggered bursts origin (i.e. both scenarios related to a GRB pointing towards the Earth) rather than to an orphan afterglow (Cenko et al. Reference Cenko2013).
$\lower.75ex \hbox{$\sim $} \llap{\raise.27ex \hbox{$>$}}\,$
0.8° (Soderberg et al. Reference Soderberg, Nakar and Berger2006) on the typical opening angle of GRBs were inferred from OA searches. However, to date no orphan afterglow has been confirmed. Some transients have been identified as possible OA candidates through archival searches both at radio frequencies (e.g. see Murphy et al. Reference Murphy2012; Bell et al. Reference Bell2011 for a summary of radio OA search results) and in the optical band (e.g. Rau, Greiner, & Schwarz Reference Rau, Greiner and Schwarz2006; Malacrino et al. Reference Malacrino2007; Zou, Wu, & Dai Reference Zou, Wu and Dai2007) but none of these has been confirmed as an orphan GRB afterglow. Even the very recent discovery (Cenko et al. Reference Cenko2013) of an optical transient by the Palomar Transient Survey (PTF) seems favour a “dirty fireball” or an untriggered bursts origin (i.e. both scenarios related to a GRB pointing towards the Earth) rather than to an orphan afterglow (Cenko et al. Reference Cenko2013).
A possible strategy (Soderberg et al. Reference Soderberg, Nakar and Berger2006; Bietenholz et al. Reference Bietenholz, De Colle, Granot, Bartel and Soderberg2013) for identifying off–axis GRBs is to observe a considerable radio emission from type Ib/c SNe at late times (i.e. years after the SN explosion). The estimate of the size of the SN event at late epochs allows us to verify if the SN had a relativistic jet. A handful of SNe were found to have a bright radio emission: SN 2001em - (Granot & Ramirez Ruiz Reference Granot and Ramirez Ruiz2004), SN 2007gr (Paragi et al. Reference Paragi2010) and SN 2009bb (Soderberg et al. Reference Soderberg, Brunthaler, Nakar, Chevalier and Bietenholz2010), SN 2003gk (Bietenholz et al. Reference Bietenholz, De Colle, Granot, Bartel and Soderberg2013). However either subsequent revision of the radio observations (Soderberg et al. Reference Soderberg2010a) or VLBI observations (Bietenholz, Bartel, & Rupen Reference Bietenholz, Bartel and Rupen2010; Bietenholz et al. Reference Carilli and Rawlings2013) showed that these events are non–relativistic SN Ib/c. Only SN 2009bb could be considered as a transition event between the class of SNe and GRBs (Soderberg et al. Reference Soderberg2010a).
If GRBs have a jet, OA should exist and they should be detected by wide field deep surveys. Here we consider the standard model of a uniform jet for GRBs but the detection rate of OA has been explored (Rossi, Perna, & Daigne Reference Rossi, Perna and Daigne2008) also for a universal structured jet model (Rossi, Lazzati, & Rees Reference Rossi, Lazzati and Rees2002; Zhang & Meszaros Reference Zhang and Meszaros2002).
If the non detection of OA is due to the low sensitivity of past surveys, future deep and wide field transient surveys could succeed in detecting OA and, as mentioned above, they could represent a considerable fraction of the detected transient population (e.g. Frail et al. Reference Frail, Kulkarni, Ofek, Bower and Nakar2012). However, one challenge is how to disentangle the population of GRB OA from other possible sources producing similar transients. In the radio band, the detection of GRB afterglows (Chandra & Frail Reference Chandra and Frail2012) benefits from the fact that the brightest phase of the emission happens on timescales of few days (for GRBs observed on–axis), because initially suppressed by self–absorption. This allows us to detect and follow the GRB radio emission when the flux at higher frequencies is already below the sensitivity of available instruments. Late time observations of radio emission from GRBs is fundamental for constraining some key parameters of these sources (e.g. Berger, Kulkarni, & Frail Reference Berger, Kulkarni and Frail2003, Reference Berger, Kulkarni and Frail2004) and for estimating their global energetic (Frail et al. Reference Frail, Kulkarni, Nicastro, Feroci and Taylor1997; Reference Frail, Metzger, Berger, Kulkarni and Yost2004; Shivvers & Berger Reference Shivvers and Berger2011; Sironi & Giannios Reference Sironi and Giannios2013).
We are now entering a new era of radio surveys. In preparation for the Square Kilometre Array (SKA, Carilli & Rawlings, Reference Carilli and Rawlings2004), that will represent a giant leap forward in survey depth at all GHz and sub-GHz frequencies, there are several pathfinders that will become operative within the next few years. In the sub-GHz regime, both the Low Frequency Array for Radio-astronomy (LOFAR, van Haarlem et al. Reference van Haarlem2013) and the Murchinson Widefield Array (MWA, Bowman et al. Reference Bowman2013, Tingay et al. Reference Tingay2013) will scan the sky with unprecedented survey speed, thanks to their field of view. Nonetheless as far as the search for OA is concerned, these will be likely limited to the exceptionally bright sources. In the GHz band, the most promising telescopes -in terms of dynamic range and fields of view- for the systematic search for transients are the Australian SKA-Pathfinder (ASKAP, Johnston et al. Reference Johnston2007), the Aperture Tiles In Focus (AperTIF) experiment, a wide field upgrade to the Westerbrok Synthesis Radio Telescope (Verheijen et al. Reference Verheijen2008), and the MeerKAT telescope. While the MHz telescopes are already operative, the GHz SKA pathfinders will take first light in the next 2–5 years.
In order to study the detectability of OA with on–going and future surveys it is necessary to know the emission properties (timescales and flux level) of the population of OA which depend on the properties (energetics, distance scale, jet opening angle) of the population of GRBs. In this paper we use a population synthesis code PSYCHE (Ghirlanda et al. Reference Ghirlanda2013a; Reference Ghirlanda2013b) summarised in Section 2 which has already been used to predict the detectability of on–axis GRB afterglows in the radio band (Ghirlanda et al. Reference Ghirlanda2013b). Here we explore for the first time with such a code the radio emission properties of Orphan Afterglows (Section 3) and compare with the current limits on the detection rates at radio frequencies (Section 4). We explore the detectability of OA by future radio surveys in Section 5.
2 THE POPULATION OF GAMMA RAY BURSTS
Ghirlanda et al. (Reference Ghirlanda2013a - G13 hereafter) built a population synthesis code which simulates GRBs (i) distributed in the Universe up to z = 10 according to the GRB formation rate (Salvaterra et al. Reference Salvaterra2012), (ii) with initial bulk Lorentz factors Γ0 and (iii) jet opening angles θjet extracted from log–normal distributions. Each burst is oriented with respect to the line of sight with a viewing angle θview (distributed as the sin θview probability density function). The starting assumption of PSYCHE is that all GRBs have a standard comoving frame energy E′γ = 1.5 × 1048 erg and a unique comoving frame prompt emission peak energy E′p = 1.5 keV. This assumption is motivated by the clustering of these quantities found when correcting for the beaming factor Γ0, estimated from the peak of the afterglow light curve (Liang et al. Reference Liang, Yi, Zhang, Lü, Zhang and Zhang2010; Ghirlanda et al. Reference Ghirlanda2012; Lu et al. Reference Lu2012).
The energetic of each simulated burst is then determined by Γ0 (E γ = Γ0 E′γ) and the isotropic equivalent energy by Γ0 and θjet (E iso = Γ0 E′γ/(1-cosθjet)). The simulation free parameters (e.g. the parameters of the log–normal distributions of Γ0 and θjet) are determined by reproducing the observed properties of the GRB samples observed by different satellites: (a) the flux distribution and (b) the empirical E p − E iso correlation of BAT6, i.e. a complete sample of bright Swift GRBs (Salvaterra et al. Reference Salvaterra2012; Nava et al. Reference Nava2012), (c) the flux and fluence distributions of GRBs detected by Fermi and by BATSE-CGRO. In particular, constraint (a) is used to normalise the GRB population so that the number of simulated bursts with peak flux > 2.6 ph cm− 2 s− 1 matches the rate of GRBs ( ≈ 15 sr− 1 yr− 1) detected by Swift-BAT above this flux threshold.
The GRBs used as observational constraints by PSYCHE are bursts that are pointing towards the Earth (i.e. with θjet > θview), indeed their prompt emission has been detected by different satellites (Swift, Fermi, CGRO). However, the code simulates also GRBs seen off–axis. This is because one of the scopes of G13 was to describe the parent population of bursts, of which only a minor fraction (with θjet > θview) can be detected in the γ–ray band. The simulated population of GRBs is shown in Figure 1 where the viewing angle θview is plotted against the jet opening angle θjet. It is evident that the jet angle distribution θjet is log–normal, while the clustering of the population towards large θview values is the effect of the probability function of θview.

Figure 1. Viewing angle (θview) versus jet opening angle (θjet) of the simulated population of GRBs (G13). The solid line of equality separates GRBs pointing to the Earth (blue symbols - with θjet ⩾ θview) from the bulk of the population of GRBs not pointing to the Earth (black symbols - with θjet ⩽ θview) which can be detected as Orphan Afterglows.
The population is composed by a minor fraction ( ~ 2.4%) of GRBs that are “pointing” towards the Earth (i.e. with θjet > θview) which can be detected by γ–ray detectors (blue symbols in Figure 1) and a majority of bursts that are off–axis with θjet < θview (black symbols in Figure 1). The latter are events that can be potentially detected at any frequency except that in the γ–ray band and are called OA. Therefore, a description of the properties of the entire GRB population should also consider the GRBs that are off–axis and are detectable only as OA. According to the results of PSYCHE, the ratio of the off–axis to on–axis bursts (i.e. black vs. blue dots in Figure 1) is ~ 40, smaller than the typical value obtained by assuming that all GRBs have θjet = 3°. This is due to the distribution of θjet that we find with PSYCHE to be a log–normal (see G13 for details). Through our simulation we find that the rate of OA is ~ 3.3 × 104 yr− 1 sr− 1 (i.e. ~ 10 yr− 1 deg− 2).
3 ORPHAN AFTERGLOW TIMESCALES
One of our aims is to derive the detectability of OAs with current and future radio surveys. We consider here the flux at the brightest phase of the OA emission. This happens at a characteristic time t v when the bulk Lorentz factor Γ(t v) = 1/sinθview. Although the flux starts to rise before this time, when the edge of the jet (that we assume here to have a sharp top-hat conical section) closer to the viewing angle becomes visible (i.e. when Γ = 1/sin(θview-θjet)), the peak flux of the orphan afterglow happens when all the jet is visible. For t ⩾ t v the light curve as seen by an observer off–axis is the same as that seen by an on–axis observer.
The peak of the OA emission is reached when the afterglow is still described by the relativistic Blandford-McKee (Reference Blandford and McKee1976) self similar solution which relates the bulk Lorentz factor Γ(R) with the distance R from the central source,
where E k is the kinetic energy driving the expansion of the fireball into the interstellar medium of density n. The kinetic energy is related to the prompt emission γ–ray energy E iso/η ≈ E k through the efficiency η.
We can derive the time t v when Γ = 1/sinθview expressing through Equation (1) the distance R v when this transition occurs:
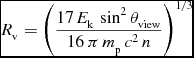 \begin{equation}
R_{\rm v} = \left(\frac{17\, E_{\rm k}\, \sin ^2 \theta _{\rm view}}{16\, \pi \, m_{\rm p}\, c^2\, n} \right)^{1/3}
\end{equation}
\begin{equation}
R_{\rm v} = \left(\frac{17\, E_{\rm k}\, \sin ^2 \theta _{\rm view}}{16\, \pi \, m_{\rm p}\, c^2\, n} \right)^{1/3}
\end{equation}
The corresponding time t v can be derived by integrating:
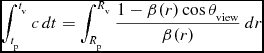 \begin{equation}
\int _{t_{\rm p}}^{t_{\rm v}} c\, dt = \int _{R_{\rm p}}^{R_{\rm v}} \frac{1-\beta (r)\cos \theta _{\rm view}}{\beta (r)}\, dr
\end{equation}
\begin{equation}
\int _{t_{\rm p}}^{t_{\rm v}} c\, dt = \int _{R_{\rm p}}^{R_{\rm v}} \frac{1-\beta (r)\cos \theta _{\rm view}}{\beta (r)}\, dr
\end{equation}
The lower boundary of the integrals (R p, t p) correspond to the distance/time from which the BM solution is valid. Although the transition from the coasting phase (when the fireball is moving with constant velocity Γ0) to the deceleration phase is smooth (see e.g. Nava et al. Reference Nava2013), we derive R p by extrapolating backwards the BM solution to the end of the coasting phase, i.e. R p = (17E k/16πm p c 2 nΓ2 0)1/3. For the typical parameters of our synthetic GRB population (R p, t p) ≪ R v, t v) so that the estimate of t v is dominated by R v.
Following G13 (see also Section 4), we assume the ISM density n uniformly distributed between 1 and 30 cm− 3 and a typical value of the radiative efficiency η = 20%. Figure 2 shows the differential (main panel) and cumulative (inset) distribution of the time of the peak of the OA, t v, of the simulated population of GRBs seen off–axis (solid blue line). The OA emission peaks on average a few years after the GRB event.

Figure 2. Differential and cumulative (inset) distributions of the time when orphan afterglows peak (blue solid line) and of the duration of the orphan afterglow emission (red dashed line).
However, the relevant timescale for OA studies and detection (Section 5) is their duration because there is no starting reference time coincident with the GRB prompt emission (which is undetected for OA). The time when the OA emission starts to be visible t s, at a very low flux level, is when Γ = 1/sin(θview − θjet). Then the flux rises reaching a peak at t v and decays afterwards in the same way as it would if seen from an on–axis observer. In order to define a duration, we consider the difference between the time when the jet becomes non–relativisic t NR (i.e. when Γ = 1, e.g. Livio and Waxman Reference Livio and Waxman2000) and the time when the OA starts to be visible (t s). The OA duration distribution is shown by the dashed (red) histograms in Figure 2 (differential and cumulative in the main plot and inset, respectively). The duration of the OA emission is slightly smaller than the typical timescales corresponding to the peak of the same emission confirming that OA are slow transients.
4 ORPHAN AFTERGLOW FLUXES
To characterise the flux distribution of OA we have coupled the population synthesis code (G13) with an emission model for the afterglow. We use the afterglow Hydrodynamic Emission (HE) code of van Eerten & MacFadyen (Reference van Eerten and MacFadyen2012a, Reference van Eerten and MacFadyen2012b) obtaining a code (PSYCHE) which has already been used to study the radio emission properties of on–axis GRBs (Ghirlanda et al. Reference Ghirlanda2013b). The HE code is based on a set of jet hydrodynamic 2D simulations that describes the evolution of the jet expansion into a constant density medium from the ultra–relativistic phase to the sub–relativistic one. This code assumes synchrotron emission with self absorption from a population of electrons accelerated at the shock front with a power law energy distribution with slope p. The fraction of the shock energy shared between electrons and magnetic field is parametried by the ε e and ε B parameters.
In addition to the GRB parameters (redshift z, jet opening angle θjet, viewing angle θview, isotropic equivalent kinetic energy E k) PSYCHE requires to set n, ε e and ε B . The values of these parameters will differ from burst to burst. Ghirlanda et al. (Reference Ghirlanda2013b) shows that with typical values of ε e = 2 × 10− 2 and ε B = 8 × 10− 3 and p = 2.5 (see also Ghisellini et al. Reference Ghisellini, Nardini, Ghirlanda and Celotti2009), PSYCHE can reproduce the radio flux distribution of the BAT6 Swift sample.
Through PSYCHE we can compute the flux density of the population of OA at typical characteristic frequencies: considering the current radio facilities, we choose three GHz frequencies (1.4, 5 and 8.4 GHz) and two MHz frequencies (200 and 600 MHz). Figure 3 shows the cumulative peak flux distribution of OA radio afterglows at these frequencies.

Figure 3. Cumulative flux distribution of orphan afterglows at GHz and MHz observing frequencies (color codes as shown in the legend). The dashed lines (with slope − 1.7 and − 0.4) are shown for reference. The dot–dashed (cyan) line shows the flux distribution (at 8.4 GHz) of the subsample of GRBs with θview < 10° which determines the break. The current (3σ) upper limits on the rate of orphan afterglows detected in archival searches and radio surveys are shown (with colour codes corresponding to the observing frequencies) and the corresponding survey names/references are shown in the legend. The vertical dashed lines (colour codes corresponding to the sampling frequencies) represent the 5σ flux limits (Table 1) that will be reached by current and future radio surveys (labelled with the corresponding instrument/survey name). The grey shaded thick line represents the predictions of Frail et al. (Reference Frail, Kulkarni, Ofek, Bower and Nakar2012) at 8.4GHz.
The distributions of Figure 3 show the rate of OAs in deg− 2 yr− 1. The bright end of the flux distribution extends to the mJy level at higher frequencies, although the rate of these bright events is very small. For instance, at 8.4 GHz (blue line in Figure 3), there are ~ 2 × 10− 3 events deg− 2 yr− 1 brighter than 1 mJy. This rate is smaller by a factor 10–50 with respect to the predictions of Levinson et al. (Reference Levinson, Ofek, Waxman and Gal-Yam2002) rescaled for our different assumptions. This could be due to the assumptions of that work (e.g. a unique beaming factor and energetic of GRBs and the description of the OA flux at the trans–relativistic transition). Our model instead assumes the proper distributions of the jet opening angles and GRB energetics (as derived through the population synthesis code of G13) and uses the HE code to describe the OA emission throughout the relativistic to non–relativistic phase.
The flux distributions shown in Figure 3 are consistent with a slope − 1.7 at high fluxes and assume a flatter slope − 0.4 at lower flux levels (grey dashed lines in Figure 3). The bright end of the flux distribution (i.e. above 0.1 mJy) is consistent with the prediction of Frail et al. (Reference Frail, Kulkarni, Ofek, Bower and Nakar2012) for the same flux interval (shown by the shaded grey thick line in Figure 3). However, we note that our code extends the flux energy range far below this limit where there is a considerable flattening of the flux distribution. This is a relevant point for the prediction of the rate of OA detectable by future deep radio surveys. The high end of the flux distribution is dominated by GRBs with small opening angles θjet observed at small viewing angles θview (low left corner of the θview-θjet plane in Figure 1). In G13 we have shown that small θjet correspond to GRBs with large Γ0, which have large energetics. The break of the flux distribution corresponds to a viewing angle θview ≈ 10° (as shown by the dot–dashed cyan line in Figure 3). The slope of the flux distribution below the break is due to the superposition of the flux distributions of progressively more GRBs with larger θview.
5 ORPHAN AFTERGLOWS RADIO DETECTION RATES
5.1 Present limits
Searches of transients in radio archival observations or radio surveys (Levinson et al. Reference Levinson, Ofek, Waxman and Gal-Yam2002; Gal-Yam et al. Reference Gal-Yam2006; Bannister et al. Reference Bannister, Murphy, Gaensler, Hunstead and Chatterjee2011; Bell et al. Reference Bell2011; Bower and Saul Reference Bower and Saul2011; Bower et al. Reference Bower, Saul, Bloom, Bolatto, Filippenko, Foley and Perley2007, Reference Bower2010; Croft et al. Reference Croft2010; Frail et al. Reference Frail, Kulkarni, Ofek, Bower and Nakar2012; Carilli et al. Reference Carilli, Ivison and Frail2003; Matsumura et al. Reference Matsumura2009; Lazio et al. Reference Lazio2010) set upper limits on the sky density of transients.
Detection of radio transients is, however, only the first step towards the identification of OA, because many other astronomical objects can produce radio transients (see e.g. Murphy et al. Reference Murphy2012 for a recent review) and the absence of any γ–ray trigger for OA prevents their classification as events related to GRBs seen off–axis. Of the nine candidate radio transients identified by comparing the NVSS (Condon et al. Reference Condon, Cotton, Greisen, Yin, Perley, Taylor and Broderick1998) and FIRST (White et al. Reference White, Becker, Helfand and Gregg1997) radio surveys at 1.4 GHz (Levinson et al. Reference Levinson, Ofek, Waxman and Gal-Yam2002), five were rejected as false triggers and two were classified as a radio SN and as an artefact in the data by Gal-Yam et al. (Reference Gal-Yam2006) through extensive follow up and multi wavelength observations. Similarly, the detection rates (10 transients at 8.4 and 4.8 GHz) originally reported by Bower et al. (Reference Bower, Saul, Bloom, Bolatto, Filippenko, Foley and Perley2007) through the analysis of archival VLA observations, were later rejected by an independent analysis of the same data sets (Frail et al. Reference Frail, Kulkarni, Ofek, Bower and Nakar2012). The fields of the VLA (at 1.4, 4.8 and 8.4 GHz), recently analysed by Bell et al. (Reference Bell2011), are distributed over more than 20 years and have typical separations of few days or a month but do not show any radio transient detected down to a limiting flux of 8 mJy. There were also works that used extensive observations of a single field (e.g. the archival VLA observations of the 3C 286 field - Bower & Saul Reference Bower and Saul2011 or the Lockman Hole - Carilli et al. Reference Carilli, Ivison and Frail2003) all giving upper limits on the detection of radio transients at some flux level. Murphy et al. (Reference Murphy2012) and Bell et al. (Reference Bell2011) summarised these results.
Figure 3 shows the upper limits derived from Table 3 of Murphy et al. (Reference Murphy2012) at the corresponding flux limit of the survey. The limits on the radio transients density have been converted into detection rate limits considering the typical timescales of the surveys. All the current upper limits are consistent with the flux distribution of the population of OA derived with PSYCHE. The different colours of the upper limits in Figure 3 correspond to the characteristic radio frequency of the survey and should be compared with the corresponding line (same colour coding) of the flux distribution. All the current limits correspond to relatively high flux levels, larger than 0.1 mJy.
5.2 Future surveys
Considering the main future surveys that will be performed by the SKA and its pathfinders we report in Table 1 the detection rates (col.4) expected considering a 5σ flux limit (col.3). We are aware that the continuum sensitivity limits are still somewhat uncertain, but we adopt fiducial values from the available literature Footnote 1 .
Table 1. Detection rates of OA by future radio telescopes. For each survey the observing frequency (col.2) and the 5σ sensitivity limit (col.3) is reported. The rates (col.4) are derived from the flux density distributions shown in Figure 3.
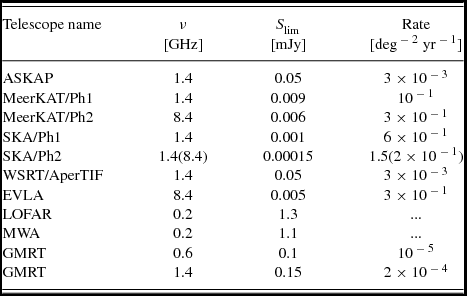
We also note that the future survey design is still on its way and the two leading parameters, i.e. the field of view and the sensitivity, should be considered in estimating the rate of AO detectable by a given survey at a given frequency. Here (Table 1) we give the detection rates in units of OA yr− 1 deg− 2 at fiducial 5σ sensitivity limits, so that if the sensitivity will remain almost unchanged the rate can be obtained multiplying for the field of view. If these numbers will change substantially for a given survey, Figure 3 should be used to derive the OA rate at a different sensitivity limit for surveys operating at different frequencies. As far as the MHz telescopes are concerned, we predict that the peak OA fluxes will be 50–100 times fainter than the ~ mJy sensitivity provided.
In order to explore the population of OA at radio frequencies it is fundamental to go deeper than current limits. Considering the slopes of the flux distributions (Figure 3) one should go deeper in sensitivity above the break of the flux distribution and instead consider a wider field of view at fluxes below the break in order to maximise the rate of detected OA.
Current searches for radio transients have used available radio observations (mostly archival) which are not homogeneously spaced in time. In general these searches are sensitive to radio transients which are present in some observation and then disappear (or the other way around). The timescale of the transients that are detectable is therefore related to the timescale separating subsequent observations (i.e. the survey cadence). Radio OA are long lived transients and it is important to estimate how long they last. While we have defined their duration in Section 3 considering the separation between two characteristic “dynamical” timescales, here we want to describe the time interval during which the OA is above a certain flux threshold S lim corresponding to a given survey limit.
The number of OA above threshold and their average duration depends on S lim. Decreasing S lim (i.e. for a deeper survey): (i) the fraction of OA that can be detected with flux F ⩾ S lim increases and (ii) their “duration above threshold”= T increases. We have computed for all the simulated OA the time interval during which their emission (at a given frequency) is above S lim. Figure 4 shows the average duration T above a certain S lim as a function of S lim. The reported numbers are the all sky number of OA in units of yr− 1 which can be detected given that S lim. The average duration T above S lim increases when deeper survey limits are considered. We note that future surveys (shown by the vertical dotted lines in Figure 4) can detect a large number of OA per year (full sky) provided that their cadence is smaller or similar to the typical duration of OA (as shown in Figure 4). For example, considering the ASKAP (or WSRT) flux limit of 50μJy at 1.4 GHz, there are ~ 125 OA yr− 1 on all the sky. Out of these, ~ 0.1 yr− 1 could be detected in the VAST survey field of view of 30 deg2. These sources could be detected as on–off transients in subsequent exposures separated at least by one week up to one month.

Figure 4. Average OA duration above S lim as a function of the survey limiting flux. Blue asterisks are for the 8.4 GHz and red circles for 1.4 GHz (the latter are slightly displaced along the abscissa for clarity). The reported numbers correspond to the total number of OA that are above S lim at their peak (in units of yr− 1 all sky). The 5σ limiting fluxes of the current and future surveys are reported.
In G13 we derived that ~ 0.3% of SN Ib/c can produce a GRB event. This percentage refers to all GRBs, i.e. those pointing to the Earth (i.e. detected as γ–ray events) and those pointing in other directions (detectable as OAs). If SN Ib/c are GRBs oriented away from the observer line of sight, they should be detected at late times when the afterglow emission has decelerated enough to encompass, with its beaming angle, the observer viewing angle θview. Soderberg et al. (Reference Soderberg, Nakar and Berger2006 - S06) and Bietenholz et al. (Reference Carilli and Rawlings2013 - B13) performed radio surveys of a sample of SN Ib/c, the putative progenitors of long–duration GRBs. Since their combined sample consists of 112 SN, according to the finding of G13 we should expect that ~ 0.34 SN Ib/c of their sample can harbour a GRB jet, i.e. we would expect no detection. They observed these SNæat late times (years after the explosion) at 8.4 GHz. S06 and B13 report indeed upper limits on the late time radio flux of the monitored sources with the exception of SN2001em (see S06), and SN2003gk (see B13), which are in fact detected. Nonetheless, further monitoring of these two events in the radio band and through VLBI observations, excluded that they produced a relativistic jet. We show in Figure 5 the upper limits on the 8.4 GHz flux of the SN Ib/c observed by S06 and B13 which are all consistent with the density contour of the distribution of the simulated population of OA. The 1, 2, and 3σ contours represent the boundary containing respectively 68.2%, 95.4%, and 99.7% of the points distribution in the plane F peak – t peak.

Figure 5. Density contours (1,2 and 3σ as labelled) representing the distribution of the flux (at 8.4GHz) of the OA population versus the time when their light curve peaks. The 3σ upper limits of the SNIb/c observed in the radio band by Soderberg et al. Reference Soderberg, Nakar and Berger2006 (green triangles) and by Bietenholz et al. Reference Carilli and Rawlings2013 (red triangles) are shown. Filled circles are the two detections at radio frequencies, i.e. SN 2001em and SN 2003gk.
6 SUMMARY AND DISCUSSION
Orphan afterglows are GRBs whose emission is detectable only during the afterglow phase (at optical/NIR and radio frequencies). Their prompt γ–ray emission is unobservable because the viewing angle θview is larger than the jet opening angle θjet (off–axis GRBs). In these events the afterglow emission becomes observable when the bulk Lorentz factor, which is decreasing during the afterglow phase, becomes Γ ~ 1/θview. After this time, which represents the peak of the OA light curve, the emission is similar to that for an observer within the jet opening angle.
OA make up a majority of the population of GRBs. However, none have been observed so far, do to their lack of a prompt emission trigger. Their detection is possible as transients in deep/wide field surveys. However, so far no detection of OA has been confirmed by searches in archival optical/radio observations. In current and future surveys OA might represent a considerable fraction of detected transients.
In this paper we have used the results of a population synthesis code for GRBs (G13) that simulates the entire population of GRBs including off-axis events and is anchored to reproduce some observational constraints of the population of GRBs detected Fermi and CGRO with particular emphasis on the constraints given by the BAT6 complete Swift sample (Salvaterra et al. Reference Salvaterra2012).
We have explored the properties of the population of off–axis GRBs (see Figure 1 - black symbols) in terms of their radio emission. We have computed the radio flux density of the OA population (representing ~ 97% of the entire GRB simulated population) at the time when the OA light curve reaches its peak (Figure 2) which is of the order of few years after the prompt trigger. However, the lack of any prompt emission (i.e. γ–ray trigger) in OA, requires to compute the timescale of their duration which, given the typical rise/decay long–term evolution of the afterglow flux, can be of the same order of the peak time. This suggest that OA in the radio band should be slow transients.
We have constructed the cumulative flux distribution at different radio frequencies (GHz and MHz) that shows a high flux tail with a slope consistent with − 1.7 (Figure 3) and a break at a frequency dependent flux below which the slope becomes flatter ( − 0.4). This is due to the combination of the θjet distribution of the population of simulated bursts with the viewing angle θview probability function: at approximately 10° the product of the θjet log–normal distribution (resulting from the population code of G13) and of the probability density of θview is maximised. This accounts for the slope change of the flux distributions in Figure 3, the break of the flux distribution is shifted to lower fluxes at lower frequencies because the radio emission is in the self absorbed regime of the synchrotron spectrum.
In general, from Figure 3 we note that very bright OA with flux at the 1 mJy level are rare. This is the central flux of the current radio searches/surveys that have been searching for OAs. Our population is consistent with the limits given by these surveys. Totani & Panaitescu (Reference Totani and Panaitescu2002) derived the flux distribution of orphan afterglows based on 10 bright GRB afterglows. Our estimates are consistent in the bright flux end with their but we predict a lower number of OA at low fluxes (below the break of our flux distribution). This is due to the modelling, in our case, of the GRB jet opening angle distribution (G13).
In G13 we derived that ~ 0.3% of SN Ib/c may harbour a GRB, i.e. in other words the great majority of the putative progenitors of GRBs do not produce a relativistic jet. When compared to the combined samples of S06 and B13, which comprise 112 SN Ib/c, there were indeed only two detections and we statistically expect none of them to be an off-axis GRB. Both SN 2001em and SN 2003gk were successively showed not to expand at relativistic velocity, arguing against their being genuine OAs. Finally, we showed (in Figure 5) that all upper limits on SN Ib/c radio emission at late times are indeed consistent with the distribution of GRB OAs in the plane F peak – t peak.
7 ACKNOWLEDGEMENTS
We thank the PRIN/INAF C41J12000020005 for financial support. DB and TM acknowledge the support of the Australian Research Council through grant DP110102034. The Centre for All-sky Astrophysics is an Australian Research Council Centre of Excellence, funded by grant CE110001020. The anonymous referee is acknowledged for his/her useful comments.









