1 INTRODUCTION
Many important extra-galactic measurements rely on robust measurement of the fluxes and structural properties for large samples of galaxies (e.g. Allen et al. Reference Allen, Driver, Graham, Cameron, Liske and de Propris2006, Simard et al. Reference Simard, Mendel, Patton, Ellison and McConnachie2011, Lackner & Gunn Reference Lackner and Gunn2012, Kelvin et al. Reference Kelvin2012). Examples include the bivariate brightness distribution (e.g. Smith et al. Reference Smith, Loveday and Cross2009), the mass-size relation (e.g. Williams et al. Reference Williams, Quadri, Franx, van Dokkum, Toft, Kriek and Labbé2010), the Tully–Fisher relation (e.g. Mocz et al. Reference Mocz, Green, Malacari and Glazebrook2012), and the fundamental plane along with studies of galaxy formation, evolution, and internal structure (e.g. Gunawardhana et al. Reference Gunawardhana2011). In the current data-rich era, it is typically the systematic rather than random errors which now dominate this process. The drive to reduce systematic errors and further constrain models therefore demands high-precision galaxy photometry and high-fidelity spatial profiling, hence the need for more sensitive imagery with greater spatial resolution over substantive areas of sky. To this extent, a number of wide-field surveys such as the Sloan Digital Sky Survey (SDSS; York et al. Reference York2000; Abazajian et al. Reference Abazajian2009), the 2-Micron All Sky Survey (2MASS; Skrutskie et al. Reference Skrutskie2006), the Panoramic Survey Telescope and Rapid Response System (Pan-STARRS), the Galaxy Evolution Explorer (GALEX; Martin et al. Reference Martin2005) Medium Imaging Survey (MIS; Morrissey et al. Reference Morrissey2007), the VLT Survey Telescope (VST) Kilo-Degree Survey (KIDS; Arnaboldi et al. Reference Arnaboldi, Neeser, Parker, Rosati, Lombardi, Dietrich and Hummel2007), the UKIRT (UK InfraRed Telescope) Infrared Deep Sky Survey (UKIDSS; Lawrence et al. Reference Lawrence2007), and the VISTA (Visible and Infrared Survey Telescope for Astronomy) Kilo-degree INfrared Galaxy survey (VIKING; Arnaboldi et al. Reference Arnaboldi, Neeser, Parker, Rosati, Lombardi, Dietrich and Hummel2007) have been initiated with the aim of probing large areas of the sky deeper than preceding surveys at a variety of wavelengths. In particular, the advances in the near infrared (NIR) have been rapid and substantial, progressing from 2MASS to UKIDSS and currently VISTA VIKING.
Measuring the total flux from a galaxy, particularly in the NIR, is not a trivial undertaking—beyond a certain radius, the surface brightness drops sufficiently to be indistinguishable from background noise. Simple but crude aperture photometry methods such as setting a fixed aperture size or detection threshold ignores this problem completely. Other, more complex methods, such as those suggested by Kron (Reference Kron1980) or Petrosian (Reference Petrosian1976), are subject to bias with galaxy morphology (Graham & Driver Reference Graham and Driver2005b). An alternative approach is to fit a light profile and integrate to infinity or some fixed number of effective radii (e.g. Kelvin et al. Reference Kelvin2012). One general and commonly used profile is the Sérsic profile (Sérsic Reference Sérsic1963; Reference Sérsic and Sérsic1968; Graham & Driver Reference Graham and Driver2005a). The Sérsic equation describes how the intensity of light I from a galaxy varies as a function of radius r as follows:
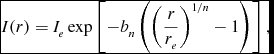 \begin{equation}
I(r) = I_e \exp \left[-b_n\left(\left(\frac{r}{r_e}\right)^{1/n} - 1\right)\right],
\end{equation}
\begin{equation}
I(r) = I_e \exp \left[-b_n\left(\left(\frac{r}{r_e}\right)^{1/n} - 1\right)\right],
\end{equation}
Sérsic parameters, magnitudes, and derived quantities can then be assembled as a function of distance and/or environment and compared to similarly defined samples drawn from numerical simulations. The Sérsic index and the bulge luminosity are particularly interesting measurements as they are known to be correlated with the mass of the central supermassive black hole (e.g. Graham & Driver Reference Graham and Driver2007; Novak, Faber, & Dekel Reference Novak, Faber and Dekel2006; Vika et al. Reference Vika, Driver, Cameron, Kelvin and Robotham2012; Savorgnan et al. Reference Savorgnan, Graham, Marconi, Sani, Hunt, Vika and Driver2013).
The Galaxy and Mass Assembly (GAMA) project (Driver et al. Reference Driver2011) is a spectroscopic and multi-wavelength imaging survey of galaxies aimed at exploring the existence, evolution, and spatial extent of mass and energy distributions from kpc to Mpc scales. GAMA combines redshifts from the AAOmega spectrograph at the 3.9 m Anglo-Australian Telescope, optical imaging from SDSS and NIR imaging from the Large Area Survey component of UKIDSS (UKIDSS-LAS) in three 12 (RA) × 5 (Dec) degree equatorial regions centred around 09 h , 12 h , and 14.5 h and (G09, G12, and G15 respectively). In the future, the GAMA team will ingest data from GALEX MIS (UV), VST KIDS (optical), VISTA VIKING (NIR), WISE (mid infrared), Herschel–ATLAS (far infrared), ASKAP DINGO (21 cm), and GMRT (325 MHz) and observe additional regions in the southern sky. In this paper, we use the GAMA dataset and processing pipeline to establish Ks -band limits to which various photometric and structural measurements, made using 2MASS, UKIDSS-LAS, and VISTA VIKING data, are reliable.
The structure of this paper is as follows. We give a brief overview of the leading wide-area NIR surveys—2MASS, UKIDSS-LAS, and VISTA VIKING—in Section 2. In Section 3, we describe how we standardised the data, assembled mosaics, estimated galaxy number counts, and recovered Sérsic profile fits and photometry for a sample of 50 123 GAMA galaxies. In Section 4, we use these to derive qualitative and quantitative limits to which various photometric and structural parameters are reliable. These data should be useful for the design of future surveys based on these data. Magnitudes are given in the AB system unless stated otherwise.
2 DATA
2.1 2MASS
During the period June 1997–February 2001, the 2MASS project (Skrutskie et al. Reference Skrutskie2006) surveyed 99.998% of the sky in the NIR. Each area of sky was viewed for 7.8 s in the JHKs bands using two 1.3 m telescopes located at Whipple Observatory, USA and Cerro Tololo, Chile. Each telescope was equipped with three 256 × 256 pixel Rockwell CCDs with a pixel scale of 2 arcsec per pixel. The three bands were imaged simultaneously. The survey achieved a limiting (AB) magnitude of J = 16.7 mag, H = 16.5 mag, and Ks = 16.2 mag at 10σ, 1σ photometric uncertainty of <0.03 mag, an astrometric accuracy of ~0.1 arcsec, and typical seeing full width at half maximum (FWHM) of 2.5–3 arcsec. In addition to images covering most of the NIR sky, the survey also produced a 471 million object point source catalogue and an extended source catalogue of 1.6 million objects. The 2MASS All-Sky Data Release, being the entire 2MASS dataset, was released to the public in 2003 MarchFootnote 2 . 2MASS has been responsible for over 1000 publications, with an aggregate of more than 32 000 citations (Driver Reference Driver2013).
2.2 UKIDSS-LAS
UKIDSS was a seven year, five survey programme which commenced in May 2005 utilising the Wide Field CAMera (WFCAM) on the 3.8 m UKIRT atop Mauna Kea, Hawaii (Lawrence et al. Reference Lawrence2007). UKIDSS-LAS aimed to provide an NIR complement to SDSS, overlapping stripes 9–16, 26–33, and part of stripe 82. UKIDSS-LAS covered 4028 deg2 of sky in theYJHK s bands to limiting magnitudes of Y = 20.9 mag, J = 20.8 mag (after two passes), H = 20.0 mag, and Ks = 20.1 mag at 5σ. UKIDSS-LAS achieved a typical seeing FWHM of <1.2 arcsec, a photometric uncertainty of <0.02 mag, and an astrometric accuracy of 0.1 arcsec.
WFCAM (Casali et al. Reference Casali2007) is an array of four 2048 × 2048 pixel Rockwell CCDs with a pixel scale of 0.4 arcsec per pixel. Raw images, or ‘pawprints’, are compressed and stored using one FITS binary HDU per CCD. Four pawprints are stitched together to form a contiguous image called a ‘tile’, covering a 0.78 deg2 field of view (including overlaps) with a combined exposure time of 40 s. UKIDSS calibration is tied at bright magnitudes to 2MASS (see Hodgekin et al. Reference Hodgekin, Irwin, Hewitt and Warren2009).
2.3 VISTA VIKING
The VISTA VIKING survey (Arnaboldi et al. Reference Arnaboldi, Neeser, Parker, Rosati, Lombardi, Dietrich and Hummel2007), commenced in April 2010 and utilises the VISTA InfraRed Camera (VIRCAM; Dalton et al. Reference Dalton2006) on the 4m VISTA telescope, located at Paranal, Chile, and operated by ESO. VIKING will image 1500 deg2 of sky in the ZYJHKs bands to target limiting magnitudes of Z = 23.1 mag, Y = 22.3 mag, J = 22.1 mag, H = 21.5 mag, and Ks = 21.2 mag at 5σ. VIKING is targeting a seeing FWHM of <1.0 arcsec.
VIRCAM is a 4 × 4 array of 2048 × 2048 pixel Raytheon CCDs with a pixel scale of 0.339 arcsec per pixel. Six pawprints, exposed for 10 s each, are assembled into a VISTA tile, which has a field of view 1.65 deg in diameter. Most of the sky in a given tile is covered at least twice.
Both UKIDSS-LAS and VIKING data are processed using the Vista Data Flow System (Emerson et al. Reference Emerson2004), with final data products being stored in the WFCAM Science Archive (WSA)Footnote 3 and the VISTA Science Archive (VSA)Footnote 4 respectively (Hambly et al. Reference Hambly2008). VISTA calibration is also tied at bright magnitudes to 2MASS.
3 IMAGE ACQUISITION AND PROCESSING
For this work, we use a subset of the G09 region above 0°declination. This region, and the coverage of the surveys within it are illustrated in Figure 1. We downloaded 1500 2MASS tiles from the 2MASS All-Sky Data Release and 315 early release VIKING pawprints from VSA containing Ks band imagery of G09 (centred on 09 h 00 m 30 s .0 + 00°15’00”.0). 928 UKIDSS-LAS images from the fourth data release were obtained from WSA and processed by Hill et al. (Reference Hill2011). We did not use VISTA VIKING tile images from VSA because they were constructed without background subtraction and therefore exhibit significant systematic large-scale sky variations.

Figure 1. Coverage of the G09 region above 0°declination in the three surveys—top: 2MASS, centre: UKIDSS-LAS, bottom: VISTA VIKING.
To process the VISTA VIKING and 2MASS images into single large-area mosaics, we applied a procedure similar to that detailed in Hill et al. (Reference Hill2011), which we summarise below.
We use a custom pipeline to extract the exposure time (t), airmass (
![]() $a = \sec \chi _\mathrm{mean} - 1 = \mathrm{(AM_{START} + AM_{END})}/2$
), and extinction (ext) from the FITS header for each image HDU. We determine an AB magnitude zero point for VISTA VIKING images using the equation:
$a = \sec \chi _\mathrm{mean} - 1 = \mathrm{(AM_{START} + AM_{END})}/2$
), and extinction (ext) from the FITS header for each image HDU. We determine an AB magnitude zero point for VISTA VIKING images using the equation:
We convert each image to a common zero point of 1 ADU = 30 mag in 1 s by multiplying each pixel by a constant 10 − 0.4(ZPtotal − 30). The sky noise, sky background, read noise, and saturation threshhold were scaled by the same factor and the gain was adjusted to keep the number of electrons unaltered.
We assembled mosaics of the renormalised images using the swarp (v2.19.1) utility (Bertin et al. Reference Bertin, Mellier, Radovich, Missonnier, Didelon, Morin, Bohlender, Durand and Handley2002). swarp is a multithread-capable image stitching, stacking, and warping tool. The construction of mosaics minimises the effect of objects being split across frames and differing zero points between frames. As we intend to match objects between surveys using astrometric measurement, it is imperative we create perfectly matched mosaics. We resample the images using the LANCZOS3 algorithm to a pixel scale of 0.339 × 0.339 arcsec in the TAN projection system (Calabretta & Greisen Reference Calabretta and Griesen2002), generating a 204500 × 79700 pixel image centred around 09 h 00 m 30s.0 +00°15’00”.0. We set swarp to subtract the background using a mesh of 512 × 512 pixels (1024 × 1024 arcsec, 205 × 205 arcsec, and 174 × 174 arcsec for 2MASS, UKIDSS-LAS, and VISTA VIKING data respectively) and a background filter size of 3 × 3 meshes. The mosaics are ~60 GB in size.
3.1 Qualitative inspection
Figure 2 shows Ks band cutouts from these mosaics for a selection of G09 galaxies with r Petrosian < 15 mag (as defined by the GAMA database; Driver et al. Reference Driver2011). Figure 3 presents cutouts of the first four galaxies in Figure 2 combined with corresponding cutouts from existing resampled GAMA SDSS DR6 mosaics (Hill et al. Reference Hill2011) to produce Ksig (=RGB) false colour images. The signal to noise ratio (S/N) and spatial resolution of the VISTA VIKING data are comparable to SDSS and are a marked improvement over UKIDSS-LAS, which in turn improves over 2MASS. The non-detection of the bottom (GAMA ID 600618) galaxy in the 2MASS dataset underscores the importance increased depth plays in the detection of low surface brightness (LSB) galaxies and galaxy components such as disks. Indeed, Bell et al. (Reference Bell, McIntosh, Katz and Weinberg2003) observe that non-detections of disk-dominated systems are a widespread phenomenon in the 2MASS dataset. The increase in depth between UKIDSS-LAS and VISTA VIKING is also clear with the non-detection of the disks of some galaxies and the increased visual size of the ellipticals despite identical scaling.

Figure 2. Ks band images of a sample of G09 galaxies; left: 2MASS, centre: UKIDSS-LAS, right: VISTA VIKING; from left to right then top to bottom: GAMA IDs 204839, 205085, 209698, 214250, 214363, 216670, 278390, 278802, 278847, 279905, 279908, 303010, 303096, 325007, 3768802, 380578, 526797, and 600168. The cutout radius is 15 arcsec.

Figure 3. Ksig = RGB false colour images of the first four galaxies (GAMA IDs 204839, 205085, 209698, and 214250) in Figure 2; left: 2MASS, centre: UKIDSS-LAS, right: VISTA VIKING.
To estimate the randomness of background noise, we visually selected 11 empty 7 × 7 pixel regions from the mosaics and computed the standard deviation of the mean pixel value of each region, which we denote as q. We compared this against a similar calculation after randomly swapping pixels between regions. A q/qswapped of 1 is indicative of perfectly uncorrelated noise while q/qswapped >>1 alludes to non-pixel scale systematic variations. 2MASS images show a high correlation between adjacent pixels (q/qswapped ~ 7) due to significant upsampling in the mosaic creation process; this is readily apparent in Figures 2 and 3. Surprisingly, VISTA VIKING (q/qswapped ~ 2.7) exhibits higher background correlation than UKIDSS-LAS (q/qswapped ~ 1) with q VIKING < q UKIDSS by about 10% prior to the swap. This appears to be the result of vastly lower random noise levels in the VISTA VIKING data—systematic variations in noise intrinsic to the VIRCAM detector on the ~10 pixel scale have become important. These variations are comparable to or smaller than the galaxies we wish to study, hence removing them without impacting measurements of galaxy flux is extremely difficult.
3.2 Surface photometry
We use sigma (Structural Investigation of Galaxies via Model Analysis; Kelvin et al. Reference Kelvin2012), part of the GAMA pipeline, to calculate Sérsic magnitudes, Sérsic indices, and half-light radii. SIGMA is a wrapper written in the R programming language (R Development Core Team 2010) around SExtractor (Bertin & Arnouts Reference Bertin and Arnouts1996), PSFex (Bertin Reference Bertin, Evans, Accomazzi, Mink and Rots2011), and galfit 3 (Peng et al. Reference Peng, Ho, Impey and Rix2010). Given the RA and DEC of a GAMA catalogued galaxy, SIGMA calculates its pixel position in the mosaic and produces a 1200 pixel square cutout centred on that galaxy. sigma invokes SExtractor to run on this cutout, producing a catalogue of stars and galaxies which are fed into PSFEx. PSFEx is a point spread function (PSF) extraction tool and is used here to generate an empirical PSF for the cutout.
Figure 4 shows the distribution of PSF FWHMs for the three surveys extracted by PSFEx. The 2MASS, UKIDSS-LAS, and VISTA VIKING surveys achieve 3σ clipped median FWHMs of 2.69 ± 0.05, 0.80 ± 0.07, and 0.87 ± 0.07 arcsec respectively. The spike at 0.8 for the 2MASS data is the result of fitting failures.

Figure 4. Histogram of measured PSF FWHMs in 0.02 arcsec bins for 2MASS, UKIDSS-LAS, and VISTA VIKING as indicated.
The PSF is used in a second SExtractor run to calculate the sky rms and an object’s Kron-like (AUTO) magnitude and radius, half-light radius, ellipticity, and CLASS_STAR probability, which are used as inputs to galfit. galfit is a 2D analysis algorithm capable of fitting multiple common astronomical profiles (e.g. Gaussian, Sérsic, exponential) to one or more objects with one or more components each within a single image frame. Within sigma, galfit is used to simultaneously fit a single Sérsic profile to the target galaxy and scaled PSFs or Sérsic profiles to secondary sources as appropriate. galfit does not estimate Poisson noise from the sources in question, however this should not be an issue for ground-based NIR observations.
We ran sigma on our SDSS r < 19.8 mag defined sample of 37 591 G09 objects that have a SURVEY_CLASS ≥2 as defined by the GAMA database (Driver et al. Reference Driver2011, their Table 4). These objects are derived from SDSS DR8 and have passed GAMA’s standard star/galaxy separation criteria (for details, see Baldry et al. Reference Baldry2010). We constrain ellipticityFootnote 5 to 0 < e < 0.95 and Sérsic indices to 0.3 < n < 15. In calculating Sérsic magnitudes, we integrate the Sérsic function (Equation 1) to 10re ; this avoids regions where little is known about galaxy light profiles.
sigma failed to converge for 8849 (23.5%), 1037 (2.8%), and 248 (0.7%) objects in the 2MASS, UKIDSS-LAS, and VISTA VIKING datasets respectively. Figure 5 shows the distribution of the entire sample as a function of the native Sérsic magnitude excluding convergence failures (upper panel) and objects for which fitting failed with respect to the input SDSS magnitude (middle panel). The increased failure rate at brighter magnitudes may be indicative of a deblending issue exacerbated by small number statistics; for Ks < 14 mag there are no more than 40 galaxies per bin. The 2MASS data show an elevated failure rate for Ks >16.5 mag, increasing from 10% to 30%. The VISTA VIKING data perform notably better to the UKIDSS-LAS data over most of the sample with a failure rate of 0 – 4% compared to 0.05 – 5% and demonstrates an improvement for objects with r >17.2 mag. The failure rate in UKIDSS-LAS increases beyond 1% at r = 18.9 mag while VISTA VIKING shows no such increase within the sample.

Figure 5. The distribution of galaxies as a function of the native Sérsic magnitude (top) and failed fits in the G09 sample as a function of SDSS r Petrosian (middle) in intervals of Δm = 0.2 mag; green: 2MASS, red: UKIDSS-LAS, blue: VISTA VIKING. The bottom panel shows the relative fraction of objects where the flux uncertainty exceeds 3σ. The solid line represents the expected number (~1%) of said outliers.
The bottom panel of Figure 5 shows the number of 3σ outliers, where σ is the standard deviation of Kx − Kv (where x = 2MASS, UKIDSS-LAS) in each bin. The fitting failures discussed above have been excluded from this panel. A likely explanation for the increase in outliers at the bright end is the detection of previously undetectable disks in VISTA VIKING. The two surveys perform similarly, with 2MASS performing slightly better—the number of 3σ outliers rises above the expected 1% threshold at 18.5 mag for 2MASS compared to 18.3 mag for UKIDSS-LAS. However, the random uncertainty in 2MASS magnitudes for Ks > 15 mag is at least 2.5 times larger than UKIDSS-LAS. Furthermore, the number of objects where sigma fails to converge is over 10 times greater for 2MASS than UKIDSS-LAS for Ks > 17.2 mag.
4 ROBUSTNESS OF FLUX AND STRUCTURE MEASUREMENTS
4.1 Star-galaxy separation limits
Figure 6 shows SExtractor’s CLASS_STAR probability versus the Ks band AUTO magnitude. We find that we can unambiguously distinguish between galaxies and stars to 14.8 mag, 16.3 mag, and 16.9 mag for 2MASS, UKIDSS-LAS, and VISTA VIKING respectively, as indicated by the blue horizontal line. However, star–galaxy separation performs poorly in the VISTA VIKING dataset for very bright objects due to saturated stars with Ks ≤ 13 mag, illustrating that increased sensitivity typically comes with the drawback of a fainter saturation magnitude if the exposure time remains constant. The red lines in the figure show our star–galaxy separation criteria. We generally consider objects with CLASS_STAR <0.8 to be galaxies however, to exclude saturated stars, we reject UKIDSS objects that do not satisfy CLASS_STAR <0.6 and Ks >13 mag. We reject VISTA VIKING objects with Ks −2 CLASS_STAR < 12.2 mag for the same reason.

Figure 6. Probability of being a star (CLASS_STAR) vs. SExtractor’s Kron-like (AUTO) Ks band magnitude; top: 2MASS, middle: UKIDSS-LAS, bottom: VISTA VIKING. The red lines illustrate star–galaxy separation criteria; items to the left and below the red line are considered to be galaxies.
4.2 Source detection
For source extraction, we run SExtractor on the mosaics generated by swarp. SExtractor is a programme that builds catalogues of sources, their positions, and Petrosian and Kron-like fluxes from an input image. We use a detection threshold of 2σ above the background, a minimum object size (SExtractor parameter DETECT_MINAREA) of 175, 7, and 5 pixels to maintain a detection area threshold of 5 native pixels and a seeing FWHM of 2.69, 0.80, and 0.87 arcsec for 2MASS, UKIDSS-LAS, and VISTA VIKING respectively. We select objects with SExtractor FLAGS < 4 to ensure reliable photometry. This resulted in a total of 54 412, 558 748, and 1 438 461 sources for 2MASS, UKIDSS-LAS, and VISTA VIKING respectively.
Figure 7 shows galaxy number counts as a function of the Ks band AUTO magnitude for the three datasets. The distributions peak at 16.3 mag, 19.9 mag, and 21.1 mag for the 2MASS, UKIDSS-LAS, and VISTA VIKING datasets respectively. However, in each case, the distribution deviates slightly from the observed exponential increase due to incompleteness, presumably caused by extended or distant objects falling below the isophotal detection threshold. To account for this effect, we set our inferred detection limits (indicated by the vertical dashed lines) 0.5 mag brighter; hence our nominal 2σ detection limits for 2MASS, UKIDSS-LAS, and VISTA VIKING are 15.8 mag, 19.4 mag, and 20.6 mag respectively. We note the VISTA VIKING data are sensitive enough to detect the change in logarithmic slope at Ks ~ 19 mag (see Christóbal-Hornillos et al. Reference Christóbal-Hornillos2009). G09 is 29% underdense out to z < 0.1 (Driver et al. Reference Driver2011), therefore there are fewer bright objects than expected.

Figure 7. Galaxy counts as a function of magnitude, binned in Δm = 0.5 mag intervals.
4.3 Surface brightness limits
Figure 8 shows the raw apparent surface brightness/apparent magnitude relation of sources detected in the VISTA VIKING dataset. We calculate the effective (or half-light) surface brightness of an object using Equation A1 of Driver et al. (Reference Driver, Liske, Cross, De Propris and Allen2005):

Figure 8. Raw apparent surface brightness as a function of magnitude of all VISTA VIKING sources, with density scaling logarithmically from sparsest (white) to densest (black). Bin sizes are 0.25 × 0.25.
Figure 9 shows the apparent surface brightness/apparent magnitude relation of galaxies for the three datasets. Both UKIDSS-LAS and 2MASS datasets have been matched against the cleaned VISTA VIKING dataset and for Ks < 18 mag, we require a source to be detected as a galaxy in both UKIDSS-LAS and VISTA VIKING. We note that SExtractor half-light radii are overestimated using the 2MASS dataset by a median factor of 1.94, presumably due to low resolution and smearing. This is corrected for in the figure. The apparent surface brightness limits are 19.9 mag arcsec−2, 21.9 mag arcsec−2, and 22.1 mag arcsec−2 for 2MASS, UKIDSS-LAS, and VISTA VIKING respectively. These will, of course, translate to brighter absolute surface brightness limits depending on each object’s individual redshift.

Figure 9. Apparent surface brightness as a function of magnitude for all three datasets, with density scaling linearly from sparsest (white) to densest (black). The red horizontal lines represent the surface brightness detection threshold. The contours contain 99.999, 99.99, and 99.9% of the data respectively. Bin sizes are 0.25 × 0.25.
4.4 Photometric accuracy limits
Figure 10 compares the consistency of SExtractor photometry derived from the 2MASS and UKIDSS-LAS datasets relative to the VISTA VIKING dataset. To calibrate for the difference between the 2MASS and UKIDSS versions of the Ks filters, we use the colour equations and the H AB − K AB offset of −0.5 mag in Hewitt et al. (Reference Hewitt, Warren, Leggett and Hodgkin2006) and a typical H Vega − K Vega≃0.25 mag (Bell et al. Reference Bell, McIntosh, Katz and Weinberg2003).

Figure 10. 2D histogram of the differences between the AUTO magnitudes derived from the 2MASS (top) and UKIDSS-LAS (bottom) datasets and VISTA VIKING as a function of the VISTA VIKING derived AUTO magnitude with 3σ clipped statistics for 13 < Ks < 16 inset. Density varies logarithmically from white (sparsest) to black (densest). Bin sizes are 0.2 mag × 0.1 mag. The histograms on the right show counts as a function of Δm with bin size 0.05. The error bars show the median and standard deviation in each 0.5 mag interval.
The 2MASS dataset struggles for objects fainter than Ks = 16 mag, where objects are consistently brighter compared to VISTA VIKING presumably due to low resolution and noise. Despite this, the 2MASS dataset shows agreement to ±0.1 mag and ±0.2 mag (1 σ, 3σ clipped) to Ks = 13.1 mag and 15.3 mag respectively. The corresponding limits for UKIDSS-LAS are 16.3 mag and 18.3 mag. These limits are given in Table 1. There appears to be a non-trivial (~0.15 mag) offset between UKIDSS-LAS and VISTA VIKING magnitudes, which decreases as a function of magnitude. A similar, but not statistically significant offset is observed when comparing Sérsic magnitudes between UKIDSS-LAS and VISTA VIKING for the SDSS sample. The cause of this offset and its variance as a function of magnitude is currently under investigation with one suggested cause being linearity issues with the calibration of at least one of the detectors (Driver et al., in prep).
Table 1. Maximum precision and 1σ limiting magnitudes for the given Δm.

4.5 Structural accuracy limits
4.5.1 Half-light radius
Figure 11 shows the ratio of half-light radii derived from sigma photometry compared to the VIKING half-light radius. Although galaxies appear to be bigger as depth increases (see Figure 2), this is a visual illusion caused by the fainter background. In fact, the effective radius from UKIDSS-LAS to VISTA VIKING stays constant with the median deviation being statistically insignificant over entire sample: −0.027 ± 0.105 (3σ clipped). The half-light radius from 2MASS to VISTA VIKING also shows a small deviation in the Sérsic parameters, with a median deviation of 0.14 ± 0.43. This suggests the Sérsic fits are reasonable, and the increased apparent size is merely a result of decreased background and noise. Considering these caveats, the half-light radius is surprisingly robust: both 2MASS and UKIDSS half-light radii are within 0.2 dex of VIKING up to 16.1 mag and 19.0 mag respectively. Table 2 shows the limiting magnitude for errors of 0.1 dex, 0.2 dex, and 0.3 dex.

Figure 11. Ratio of half-light radii as a function of the VISTA VIKING Ks magnitude. Points are coloured according to their VISTA VIKING half-light radius. The black points, lines, and error bars show 3σ clipped medians, standard deviations, and standard errors plotted at bin midpoints.
Table 2. Limiting magnitudes for the given precision (in dex) in half-light radii.

4.5.2 Ellipticity
Figure 12 shows the ratio of sigma derived ellipticities relative to the VISTA VIKING dataset. It should not be a surprise that objects with low ellipticity tend to have large fluctuations between datasets; this is due to the greater relative error. Beyond Ks >15 mag, 2MASS galaxies appear to be consistently more elliptical than the VISTA VIKING data, presumably because of a combination of noise and low resolution. For this reason 2MASS data perform rather poorly—errors increase to >0.2 dex at Ks = 14.0 mag. UKIDSS-LAS is within 0.2 dex of VISTA VIKING ellipticities down 18.4 mag. Table 3 shows the limiting magnitude corresponding to the given precisions.

Figure 12. Ratio of ellipticities as a function of the VISTA VIKING Ks magnitude. Points are coloured according to their VISTA VIKING ellipticity. The black points, lines, and error bars show 3σ clipped medians, standard deviations, and standard errors plotted at bin midpoints.
Table 3. Limiting magnitudes for the given precision (in dex) in ellipticity.

4.5.3 Sérsic index
Figure 13 presents a histogram of the recovered Sérsic indices for each dataset. The number of objects with the Gaussian n = 0.5 profile declines from 2MASS to UKIDSS-LAS then VISTA VIKING, indicating a greater number of objects are resolved in the latter datasets, particularly at the fainter magnitudes. Kelvin et al. (Reference Kelvin2012) find that the distribution of Sérsic indices in optical wavelengths is bimodal, resembling the sum of Gaussian distributions centred on n ~ 1 and n ~ 3.5 which correspond to late and early type galaxies respectively. The two peaks blend with increasing wavelength—NIR data are a more effective probe of older stellar populations that dominate early type galaxies and bulges while optical data tracks younger stellar populations more prevalent in late type galaxies. Interestingly, it appears that using the deeper VISTA VIKING dataset shifts the peaks outwards towards the exponential n = 1 and de Vaucouleurs n = 4 profiles. In particular, there are relatively more high Sérsic index objects at 15 < Ks < 18. This is a consequence of increased S/N and hence more robust sky modelling in the VIKING dataset (see Figures 2 and 14). Figure 14 demonstrates that using VISTA VIKING over UKIDSS-LAS does not result in the detection of objects at fainter magnitudes for a given Sérsic index, this may reflect a shortcoming of our sample. The 2MASS dataset does not display the double-peaked distribution at any magnitude within the sample presumably due to the lack of resolution; furthermore the bright sky makes disk (n = 1) detection difficult.

Figure 13. Histograms of Sérsic indices in the given Sérsic magnitude ranges for the three datasets convolved with a rectangular kernel of width log n = 0.05; green: 2MASS, red: UKIDSS-LAS, blue: VISTA VIKING.

Figure 14. 2D histogram of the distribution of recovered Sérsic indices as a function of Ks linearly ranging from white (sparsest) to black (densest), with bin sizes of 0.2 mag × 0.08 in log n.
Figure 15 shows the ratio of Sérsic indices as a function of the Sérsic magnitude. It is clear from the figure that the 2MASS dataset is useless even for the brightest (Ks < 14 mag) galaxies, consistently underestimating the Sérsic index due to lack of resolution. At fainter magnitudes, galaxies in the sample transition toward becoming unresolved point sources, and hence having a Gaussian profile—in Figure 13 we see the distribution peaking at lower Sérsic indices with fainter magnitudes. This transition occurs at Ks ~ 17 mag for both the UKIDSS-LAS and VISTA VIKING datasets. There is no systematic offset when comparing UKIDSS-LAS against VISTA VIKING. We find the Sérsic indices are remarkably robust, being consistent to 0.2 dex down to 17.7 mag. Table 4 shows limiting magnitudes for the given precisions.

Figure 15. Ratio of Sérsic indices as a function of the VISTA VIKING derived Sérsic magnitude. Points are coloured according to their VISTA VIKING derived Sérsic index. The black points, lines, and error bars show 3σ clipped medians, standard deviations, and standard errors plotted at bin midpoints.
Table 4. Limiting magnitudes for the given precision (in dex) in Sérsic index.

5 SUMMARY
Throughout this paper, we have demonstrated the benefits of applying galaxy photometry and profiling to more sensitive datasets. Table 5 summarises our findings. We have constructed renormalised mosaics of 2MASS, UKIDSS-LAS, and VISTA VIKING imagery of the G09 region. Using these mosaics, we establish in Figures 2 and 3 that the VISTA VIKING data are visually superior, with a higher S/N and lower sky background.
Table 5. Summary of results: Limiting magnitudes and cumulative densities per deg2.

a Bracketed values inferred from UKIDSS-LAS by adding 1.1 mag.
b Cumulative densities in N per mag per deg2.
c Sérsic magnitude.
d AUTO magnitude.
e AUTO magnitude arcsec−2.
We apply SExtractor’s star–galaxy separation to the three datasets, finding that using the VISTA VIKING data we are able to separate stars and galaxies to 0.5 mag fainter than UKIDSS-LAS and 1.5 mag fainter than 2MASS (see Figure 6). We caution that star–galaxy separation performs poorly at brighter magnitudes (Ks < 14 mag) in the VISTA VIKING data and, to a lesser extent, UKIDSS-LAS due to a lower saturation threshold. We establish SExtractor photometric limits of 15.8, 19.4, and 20.6 mag, star–galaxy separation limits of 14.8, 16.3, and 16.9 mag, and surface brightness limits of 18.6, 21.3, and 22.1 mag arcsec−2 for 2MASS, UKIDSS-LAS, and VISTA VIKING respectively. We find that there is a ~ 0.15 mag offset between VISTA VIKING and existing UKIDSS-LAS photometry which is currently under investigation.
We used sigma to fit Sérsic profiles to a sample of 37 591 SDSS galaxies with r Petrosian ≤ 19.8 mag. Using the VISTA VIKING dataset yields a decrease in the number of convergence failures compared to UKIDSS-LAS for r>17.3 mag. The VISTA VIKING failure rate does not increase appreciably at the fainter end of the sample. The effective radius is the most stable of the Sérsic parameters, with the 2MASS and UKIDSS-LAS data being within 0.2 dex of the VISTA VIKING data down to 16.1 mag and 19.0 mag respectively. The 2MASS dataset performs poorly over most of the sample when recovering ellipticities, with the deviation from VISTA VIKING rising above 0.2 dex at Ks = 14.0 mag. UKIDSS-LAS derived ellipticities are more stable, where the deviation increases beyond 0.2 dex at Ks = 18.4 mag. The 2MASS dataset yields a systematic offset when compared to VISTA VIKING in the Sérsic index for the entire sample.
ACKNOWLEDGEMENTS
We thank the anonymous referee whose comments helped improve this paper.
SKA is supported by a summer scholarship provided by the School of Physics at UWA. LSK is supported by the Austrian Science Foundation FWF under grant P23946.
GAMA is a joint European-Australasian project based around a spectroscopic campaign using the Anglo-Australian Telescope. The GAMA input catalogue is based on data taken from the Sloan Digital Sky Survey and the UKIRT Infrared Deep Sky Survey. Complementary imaging of the GAMA regions is being obtained by a number of independent survey programmes including GALEX MIS, VST KIDS, VISTA VIKING, WISE, Herschel-ATLAS, GMRT, and ASKAP providing UV to radio coverage. GAMA is funded by the STFC (UK), the ARC (Australia), the AAO, and the participating institutions. The GAMA website is http://www.gama-survey.org.
We gratefully acknowledge use of data from the ESO Public Survey programme ID 179.B-2004 taken with the VISTA telescope, data products from CASU and VSA archive operated by WFAU.
This work is based in part on data obtained as part of the UKIRT Infrared Deep Sky Survey. The UKIDSS project is defined in Lawrence et al. (Reference Lawrence2007). UKIDSS uses the UKIRT Wide Field Camera (WFCAM; Casali et al. Reference Casali2007). The photometric system is described in Hewitt et al. (Reference Hewitt, Warren, Leggett and Hodgkin2006), and the calibration is described in Hodgekin et al. (Reference Hodgekin, Irwin, Hewitt and Warren2009). The pipeline processing and science archive are described in Irwin et al (2009, in prep) and Hambly et al. (Reference Hambly2008).
This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Centre/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
APPENDIX: DESCRIPTION OF CATALOGUES
We release two catalogues with this paper. The first, 2uvsextract-trimmed.fits, contains the output from SExtractor and is described in Table A1. Bad or missing values are blank. 2uvsigma-trimmed.fits contains the output from sigma and is described in Table A2. Coverage of the entire G09 region may be incomplete for all three surveys. Missing values are denoted by -9999. The suffixes _2, _U, and _V denote 2MASS, UKIDSS-LAS, and VISTA VIKING. The prefix M01_ denotes quantities measured by galfit. These catalogues are available from http://star-www.st-and.ac.uk/~spd3/2uvsextractor-trimmed.fits and http://star-www.st-and.ac.uk/~spd3/2uvsigma-trimmed.fits.
Table A1. Description of 2uvsextract.fits.

Table A2. Description of 2uvsigma.fits.




























