Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-27T02:09:45.368Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted norm inequalities involving gradients

Published online by Cambridge University Press:  14 November 2011

C. Carton-Lebrun  and
H. P. Heinig
C. Carton-Lebrun
Affiliation:
Department of Mathematics, University of Mons, 7000 Mons, Belgium
H. P. Heinig
Affiliation:
Department of Mathematics and Statistics, McMaster University, Hamilton, Ontario, Canada
Get access Rights & Permissions [Opens in a new window]

Synopsis

Let 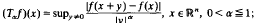then, for certain weight functions u and v and indices p,q, it is shown that ∥Tαf∥q, u≦C∥grad f ∥p, v'q > n / α holds. For α=l,p=q and u = v ≡ l this reduces to a result of M. Weiss. In addition we establish n-dimensional weighted Hardy—Littlewood type inequalities ofthe form 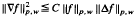for large classes of weights.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 112 , Issue 3-4 , 1989 , pp. 331 - 341
Copyright
Copyright © Royal Society of Edinburgh 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Brown, R. C. and Hinton, D. B.. Sufficient conditions for weighted inequalities of sum form. J. Math. Anal. Appl. 112 (1985), 563–577.CrossRefGoogle Scholar
2Brown, R. C. and Hinton, D. B.. Sufficient conditions for weighted Gabushin inequalities. Časopis Pěst Mat. 111 (1985), 113–122.CrossRefGoogle Scholar
3Brown, R. C. and Hinton, D. B.. Weighted interpolation inequalities of sum and product form in ℝn. Proc. London Math. Soc. (3) 56 (1988), 261–280.CrossRefGoogle Scholar
4Chanillo, S. and Wheeden, R. L.. Inequalities for the Peano maximal functions. Duke Math. J. 50 (1983), 573–603.CrossRefGoogle Scholar
5Chanillo, S. and Wheeden, R. L.. Distribution function estimates for the Marcinkiewicz integrals and differentiability. Duke Math. J. 49 (1982), 517–620.CrossRefGoogle Scholar
6Garcia-Cuerva, J. and Francia, J. L. Rubio de. Weighted Norm-Inequalities and Related Topics. Stud. Math. Appl. 116 (Amsterdam: North-Holland, 1985).Google Scholar
7Goldstein, J. A., Kwong, M. K. and Zettl, A.. Weighted Landau inequalities. J. Math. Anal. Appl. 95 (1983), 20–28.CrossRefGoogle Scholar
8Gundy, R. F. and Wheeden, R. L.. Weighted integral inequalities for the nontangential maximal function, Lusin integral and Walsh-Paley series. Studia Math. 49 (1974), 107–124.CrossRefGoogle Scholar
9Hardy, G. H., Littlewood, J. E. and Polya, G.. Inequalities (Cambridge: Cambridge University Press, 1959).Google Scholar
10Kokilashvili, V. M.. On weighted Lizorkin-Triebel spaces, singular integrals, multipliers, imbedding theorems. Proc. Steklov Inst. Math. 3 (1984), 135–161.Google Scholar
11Kwong, M. K. and , Zettl. An extension of the Hardy—Littlewood inequality. Proc. Amer. Math. Soc. 77 (1979), 117–118.CrossRefGoogle Scholar
12Kwong, M. K. and Zettl, A.. Norm inequalities of product form in weighted L P-spaces. Proc. Roy. Soc. Edinburgh Sect. A 89 (1981), 293–307.CrossRefGoogle Scholar
13Maz'ja, V. G. and Kufner, A.. Variations on a theme of the inequality (f')2 ≦2f sup ∣f”∣. Manuscripta Math. 56 (1986), 89–104.CrossRefGoogle Scholar
14Muckenhoupt, B. and Wheeden, R.. Weighted norm inequalities for fractional integrals. Trans. Amer. Math. Soc. 192 (1974), 261–274.CrossRefGoogle Scholar
15Sawyer, E.. Weighted inequalities for the one sided Hardy-Littlewood maximal functions. Trans. Amer. Math. Soc. 297 (1986), 53–61.CrossRefGoogle Scholar
16Stein, E. M.. Singular Integrals and Differentiability Properties of Functions (Princeton, NJ: Princeton University Press, 1970).Google Scholar
17Tepper-Haimo, D. (ed). Orthogonal expansions and their continuous analogues. In Proceedings Conference Southern Illinois University, Edwardsville 27–29 April 1967(Southern Illinois, University Press).Google Scholar
18Torchinsky, A.. Real Variable Methods in Harmonic Analysis (New York: Academic Press, 1986).Google Scholar
19Walter, W. (ed.). General Inequalities 5. Internat. Ser. Numer. Math. 80 (Basel: Birkhauser, 1987).CrossRefGoogle Scholar