Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-05-01T04:10:22.916Z Has data issue: false hasContentIssue false
  • English
  • Français

Sturm-Liouville operators with an indefinite weight function

Published online by Cambridge University Press:  14 February 2012

K. Daho  and
H. Langer
K. Daho
Affiliation:
Department of Mathematics, Uppsala University, Sweden
H. Langer
Affiliation:
Sektion Mathematik, Technische Universität, Dresden, G.D.R.
Get access Rights & Permissions [Opens in a new window]

Synopsis

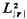Spectral properties of the singular Sturm-Liouville equation –(p−1y′)′ + qy = λry with an indefinite weight function r are studied in . The main tool is the theory of definitisable operators in spaces with an indefinite scalar product.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 78 , Issue 1-2 , 1977 , pp. 161 - 191
Copyright
Copyright © Royal Society of Edinburgh 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Achieser, N. I. and Glasmann, I. M.Theorie der linearen Operatoren im Hilbert-Raum (Berlin: Akademie-Verlag. 1968).Google Scholar
2Atkinson, F. V.Discrete and continuous boundary problems (New York: Academic Press, 1964).Google Scholar
3Atkinson, F. V., Everitt, W. N. and Ong, K. S.On the m-coefficient of Weyl for a differential equation with an indefinite weight function. Proc. London Math. Soc. 29 (1974), 368–384.CrossRefGoogle Scholar
4Bognár, J.Indefinite inner product spaces (Berlin: Springer, 1974).CrossRefGoogle Scholar
5Daho, K. and Langer, H.Some remarks on a paper by W. N. Everitt. Proc. Roy. Soc. Edinburgh Sect. A 78 (1977), 71–79.CrossRefGoogle Scholar
6Everitt, W. N. Some remarks on a differential expression with an indefinite weight function. Math. Studies, 13, 13–28 (Amsterdam: North Holland, 1974).Google Scholar
7Glazman, I. M.Direct methods of qualitative spectral analysis of singular differential operators (Moscow: Nauka, 1967). (In Russian.)Google Scholar
8Coddington, E. A. and Levinson, N.Theory of ordinary differential equations (New York: McGraw-Hill, 1965).Google Scholar
9Jorgens, K.Spectral theory of the second-order ordinary differential operators (Lectures 1962/63 at Aarhus University, 1964).Google Scholar
10Kac, I. S. and Krein, M. G.R-functions—analytic functions mapping the upper halfplane into itself. Amer. Math. Soc. Transl. 103 (1974), 1–18.Google Scholar
11Kac, I. S. and Krein, M. G.On the spectral functions of the string. Amer. Math. Soc. Transl. 103 (1974), 19–102.Google Scholar
12Krein, M. G. Introduction to the geometry of indefinite J-spaces and the theory of operators in these spaces. In 2nd Math. Summer School, Pt I, 15–99 (Kiev: Nauk. Dumka, 1965). Amer. Math. Soc. Transl. 93 (1970), 103-176.Google Scholar
13Krein, M. G. and Langer, H.On the spectral function of a self-adjoint operator in a space with indefinite metric. Dokl. Akad. Nauk SSSR, 152 (1963), 39–42, and Soviet Math. Dokl. 4 (1963), 1236-1239.Google Scholar
14Krein, M. G. and Langer, H.Über einige Fortsetzungsprobleme, die eng mit der Theorie hermitescher Operatoren im Raume IIK zusammenhängen. Teil I: Einige Funktionenklassen und ihre Darstellungen. Math. Nachr., 77 (1977), 187–236.CrossRefGoogle Scholar
15Langer, H.Zur Spektraltheorie J-selbstadjungierter Operatoren. Math. Ann. 146 (1962), 60–85.CrossRefGoogle Scholar
16Langer, H.Spektraltheorie linearer Operatoren in J-Räumen und einige Anwettdungen auf die Schar L(λ) = λ2I+ λB+ C (Tech. Univ. Dresden, Habilitationsschrift, 1965).Google Scholar
17Langer, H.Invariante Teilräume definisierbarer J-selbstadjungierter Operatoren. Ann. Acad. Sci. Fenn. Ser. Al 475 (1971).Google Scholar
18Langer, H.Verallgemeinerte Resolventen eines J-nichtnegativen Operators mit endlichem Defekt. J. Functional Analysis, 2 (1971), 287–320.Google Scholar
19Langer, H.Spektralfunktionen einer Klasse von Differentialoperatoren zweiter Ordnung mit nichtlinearem Eigenwertparameter Ann. Acad. Sci. Fenn. Ser. Al 2 (1976), 269–301.Google Scholar
20Langer, H.Zur Spektraltheorie verallgemeinerter gewohnlicher Differentialoperatoren zweiter Ordnung mit einer nichtmonotonen Gewichtsfunktion. Univ. Jyvdskyla Dept. Math. Rep. 14 (1972).Google Scholar
21Naimark, M. A.Linear differential operators Pt II (New York: Ungar, 1968).Google Scholar
22Pleijel, Å. Generalized Weyl circles. Lecture Notes in Mathematics 415, 211–226 (Berlin: Springer, 1974).Google Scholar
23Pontrjagin, L. S.Hermitean operators in spaces with indefinite metric. Izv. Akad. Nauk SSSR. Ser. Mat. 8 (1944), 243–280.Google Scholar
24Titchmarsh, E. C.Eigenfunction expansions associated with second-order differential equations, Pt Ix (Oxford: Clarendon, 1962).Google Scholar
25Weyl, H. Über gewöhnliche lineare Differentialgleichungen mit singulären Stellen und ihre Eigenfunktionen. Nachr. Akad. Wiss. Göttingen, Math.-Phys. Kl. (1910), 442–467 and in Weyl, H., Abhandlungen, Gesammelte, I (Berlin: Springer, 1968).Google Scholar