No CrossRef data available.
Article contents
Stable minimizers of functionals of the gradient
Published online by Cambridge University Press: 05 July 2019
Abstract
Let Ω ⊂ ℝn be a bounded Lipschitz domain. Let 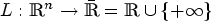 $L: {\mathbb R}^n\rightarrow \bar {\mathbb R}= {\mathbb R}\cup \{+\infty \}$ be a continuous function with superlinear growth at infinity, and consider the functional
$L: {\mathbb R}^n\rightarrow \bar {\mathbb R}= {\mathbb R}\cup \{+\infty \}$ be a continuous function with superlinear growth at infinity, and consider the functional 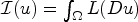 $\mathcal {I}(u)=\int \nolimits _\Omega L(Du)$, u ∈ W1,1(Ω). We provide necessary and sufficient conditions on L under which, for all f ∈ W1,1(Ω) such that
$\mathcal {I}(u)=\int \nolimits _\Omega L(Du)$, u ∈ W1,1(Ω). We provide necessary and sufficient conditions on L under which, for all f ∈ W1,1(Ω) such that 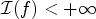 $\mathcal {I}(f) < +\infty $, the problem of minimizing
$\mathcal {I}(f) < +\infty $, the problem of minimizing 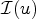 $\mathcal {I}(u)$ with the boundary condition u|∂Ω = f has a solution which is stable, or – alternatively – is such that all of its solutions are stable. By stability of
$\mathcal {I}(u)$ with the boundary condition u|∂Ω = f has a solution which is stable, or – alternatively – is such that all of its solutions are stable. By stability of 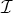 $\mathcal {I}$ at u we mean that
$\mathcal {I}$ at u we mean that  $u_k\rightharpoonup u$ weakly in W1,1(Ω) together with
$u_k\rightharpoonup u$ weakly in W1,1(Ω) together with 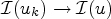 $\mathcal {I}(u_k)\to \mathcal {I}(u)$ imply uk → u strongly in W1,1(Ω). This extends to general boundary data some results obtained by Cellina and Cellina and Zagatti. Furthermore, with respect to the preceding literature on existence results for scalar variational problems, we drop the assumption that the relaxed functional admits a continuous minimizer.
$\mathcal {I}(u_k)\to \mathcal {I}(u)$ imply uk → u strongly in W1,1(Ω). This extends to general boundary data some results obtained by Cellina and Cellina and Zagatti. Furthermore, with respect to the preceding literature on existence results for scalar variational problems, we drop the assumption that the relaxed functional admits a continuous minimizer.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 5 , October 2020 , pp. 2642 - 2655
- Copyright
- Copyright © Royal Society of Edinburgh 2019





