Hostname: page-component-7bb8b95d7b-wpx69 Total loading time: 0 Render date: 2024-09-25T12:30:21.120Z Has data issue: false hasContentIssue false
  • English
  • Français

Profinite groups with restricted centralizers of commutators

Part of: Special aspects of infinite or finite groups Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  01 April 2019

Eloisa Detomi ,
Marta Morigi  and
Pavel Shumyatsky
Eloisa Detomi
Affiliation:
Dipartimento di Matematica, Università di Padova, Via Trieste 63, 35121Padova, Italy (detomi@math.unipd.it)
Marta Morigi
Affiliation:
Dipartimento di Matematica, Università di Bologna, Piazza di Porta San Donato 5, 40126Bologna, Italy (marta.morigi@unibo.it)
Pavel Shumyatsky
Affiliation:
Department of Mathematics, University of Brasilia, Brasilia-DF, 70910-900Brazil (pavel@unb.br)
Get access Rights & Permissions [Opens in a new window]

Abstract

A group G has restricted centralizers if for each g in G the centralizer 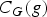$C_G(g)$ either is finite or has finite index in G. A theorem of Shalev states that a profinite group with restricted centralizers is abelian-by-finite. In the present paper we handle profinite groups with restricted centralizers of word-values. We show that if w is a multilinear commutator word and G a profinite group with restricted centralizers of w-values, then the verbal subgroup w(G) is abelian-by-finite.

Keywords

group wordsprofinite groupscentralizersFC-groups

MSC classification

Primary: 20F24: FC-groups and their generalizations
Secondary: 20E18: Limits, profinite groups 20F12: Commutator calculus
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 5 , October 2020 , pp. 2301 - 2321
Check for updates
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Dedicated to Aner Shalev on the occasion of his 60th birthday.

References

1Acciarri, C., Fernández-Alcober, G. A. and Shumyatsky, P.. A focal subgroup theorem for outer commutator words. J. Group Theory 15 (2012), 397–405.CrossRefGoogle Scholar
2Dade, E. C.. Carter subgroups and Fitting heights of finite solvable groups. Illinois J. Math. 13 (1969), 449–514.CrossRefGoogle Scholar
3Detomi, E., Morigi, M. and Shumyatsky, P.. On countable coverings of word values in profinite groups. J. Pure Appl. Algebra 219 (2015), 1020–1030.CrossRefGoogle Scholar
4Detomi, E., Morigi, M. and Shumyatsky, P.. On profinite groups with word values covered by nilpotent subgroups. Israel J. Math. 226 (2018), 993–1008.CrossRefGoogle Scholar
5Detomi, E., Morigi, M. and Shumyatsky, P.. BFC-theorems for higher commutator subgroups. Q. J. Math. to appear, arXiv:1803.04202. https://doi.org/10.1093/qmath/hay068.Google Scholar
6Dierings, G. and Shumyatsky, P.. Groups with boundedly finite conjugacy classes of commutators. Q. J. Math. 69 (2018), 1047–1051.CrossRefGoogle Scholar
7Feit, W. and Thompson, J. G.. Solvability of groups of odd order. Pacific J. Math. 13 (1963), 773–1029.Google Scholar
8Fernández-Alcober, G. A. and Morigi, M.. Outer commutator words are uniformly concise. J. Lond. Math. Soc. (2) 82 (2010), 581–595.CrossRefGoogle Scholar
9Gorenstein, D.. Finite Groups (New York: Chelsea Publishing Company, 1980).Google Scholar
10Hartley, B.. A general Brauer-Fowler theorem and centralizers in locally finite groups. Pacific J. Math. 152 (1992), 101–117.CrossRefGoogle Scholar
11Hewitt, E. and Ross, K. A.. Abstract harmonic analysis, vol. II, pp. 152 (New York-Berlin: Springer-Verlag, 1970).Google Scholar
12Huppert, B. and Blackburn, N.. Finite Groups II (Berlin: Springer Verlag, 1982).CrossRefGoogle Scholar
13Jones, G. A.. Varieties and simple groups. J. Aust. Math. Soc. 17 (1974), 163–173.CrossRefGoogle Scholar
14Kargapolov, M. I. and Merzlyakov, Yu. I.. Fundamentals of the theory of groups (Moscow: Nauka, 1982); Engl. transl. of 2nd ed. Springer, New York (1979).Google Scholar
15Kelley, J. L.. General topology (Toronto - New York - London: Van Nostrand, 1955).Google Scholar
16Khukhro, E. I.. Nilpotent groups and their automorphisms. De Gruyter Expositions in Mathematics, vol. 8 (Berlin: Walter de Gruyter & Co., 1993).CrossRefGoogle Scholar
17Khukhro, E. I. and Shumyatsky, P.. Words and pronilpotent subgroups in profinite groups. J. Aust. Math. Soc. 97 (2014), 343–364.CrossRefGoogle Scholar
18Lazard, M.. Sur les groupes nilpotents et les anneaux de Lie. Ann. Sci. École Norm. Supr. 71 (1954), 101–190.CrossRefGoogle Scholar
19Lévai, L. and Pyber, L.. Profinite groups with many commuting pairs or involutions. Arch. Math. (Basel) 75 (2000), 1–7.CrossRefGoogle Scholar
20Liebeck, M. W., O'Brien, E. A., Shalev, A. and Tiep, P. H.. The Ore conjecture. J. Eur. Math. Soc. (4) 12 (2010), 939–1008.CrossRefGoogle Scholar
21Neumann, B. H.. Groups covered by permutable subsets. J. London Math. Soc. 29 (1954), 236–248.CrossRefGoogle Scholar
22Passman, D. S.. The algebraic theory of group rings (New York: Wiley-Interscience, 1977).Google Scholar
23Ribes, L., Zalesskii, P.. Profinite groups. A Series of Modern Surveys in Mathematics,vol. 40 (Berlin: Springer-Verlag, 2000).CrossRefGoogle Scholar
24Robinson, D. J. S.. A course in the theory of groups. 2nd edn. Graduate texts in Mathematics, vol. 80 (New York: Springer-Verlag, 1996).CrossRefGoogle Scholar
25Shalev, A.. Profinite groups with restricted centralizers. Proc. Amer. Math. Soc. 122 (1994), 1279–1284.CrossRefGoogle Scholar
26Shumyatsky, P.. Applications of Lie ring methods to group theory. In Nonassociative algebra and its applications (eds Costa, R. et al. ), pp. 373–395 (New York: Marcel Dekker, 2000).Google Scholar
27Shumyatsky, P.. Verbal subgroups in residually finite groups. Q. J. Math. 51 (2000), 523–528.CrossRefGoogle Scholar
28Shumyatsky, P.. On profinite groups in which commutators are Engel. J. Aust. Math. Soc. 70 (2001), 1–9.CrossRefGoogle Scholar
29Turner-Smith, R. F.. Marginal subgroup properties for outer commutator words. Proc. London Math. Soc. (3) 14 (1964), 321–341.CrossRefGoogle Scholar
30Wiegold, J.. Groups with boundedly finite classes of conjugate elements. Proc. Roy. Soc. London Ser. A 238 (1957), 389–401.Google Scholar
31Wilson, J. C. R.. On outer-commutator words. Can. J. Math. 26 (1974), 608–620.CrossRefGoogle Scholar
32Wilson, J. S.. On the structure of compact torsion groups. Monatsh. Math. 96 (1983), 57–66.CrossRefGoogle Scholar
33Wilson, J. S. and Zelmanov, E.. Identities for Lie algebras of pro-p groups. J. Pure Appl. Algebra 81 (1992), 103–109.CrossRefGoogle Scholar
34Zelmanov, E.. Nil rings and periodic groups. Lecture Notes in Math. (Seoul: The Korean Math. Soc., 1992).Google Scholar
35Zelmanov, E. I.. On periodic compact groups. Israel J. Math. 77 (1992), 83–95.CrossRefGoogle Scholar
36Zelmanov, E. I.. Lie ring methods in the theory of nilpotent groups. In Proc. Groups'93/St. Andrews, vol. 2, London Math. Soc. Lecture Note Ser., vol. 212, pp. 567–585 (Cambridge: Cambridge Univ. Press, 1995).Google Scholar
37Zelmanov, E. I.. Lie algebras and torsion groups with identity. J. Comb. Algebra 1 (2017), 289–340.Google Scholar