No CrossRef data available.
Article contents
Positive solutions of semilinear elliptic problems with a Hardy potential
Published online by Cambridge University Press: 15 February 2019
Abstract
Let Ω ⊂ ℝN be a bounded domain and δ(x) be the distance of a point x ∈ Ω to the boundary. We study the positive solutions of the problem Δu + (μ/(δ(x)2))u = up in Ω, where p > 0, p ≠ 1 and μ ∈ ℝ, μ ≠ 0 is smaller than the Hardy constant. The interplay between the singular potential and the nonlinearity leads to interesting structures of the solution sets. In this paper, we first give the complete picture of the radial solutions in balls. In particular, we establish for p > 1 the existence of a unique large solution behaving like δ−(2/(p−1)) at the boundary. In general domains, we extend the results of Bandle and Pozio and show that there exists a unique singular solutions u such that 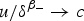 $u/\delta ^{\beta _-}\to c$ on the boundary for an arbitrary positive function
$u/\delta ^{\beta _-}\to c$ on the boundary for an arbitrary positive function 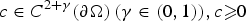 $c \in C^{2+\gamma }(\partial \Omega ) \, (\gamma \in (0,1)), c \ges 0$. Here β− is the smaller root of β(β − 1) + μ = 0.
$c \in C^{2+\gamma }(\partial \Omega ) \, (\gamma \in (0,1)), c \ges 0$. Here β− is the smaller root of β(β − 1) + μ = 0.
Keywords
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 4 , August 2020 , pp. 1791 - 1804
- Copyright
- Copyright © Royal Society of Edinburgh 2019





