Hostname: page-component-5c6d5d7d68-wbk2r Total loading time: 0 Render date: 2024-08-19T22:06:46.688Z Has data issue: false hasContentIssue false
  • English
  • Français

Positive definite temperature functions and a correspondence to positive temperature functions

Published online by Cambridge University Press:  14 November 2011

Soon-Yeong Chung
Soon-Yeong Chung
Affiliation:
Department of Mathematics, Sogang University, Seoul 121-742, Korea
Get access Rights & Permissions [Opens in a new window]

Synopsis

Positive definite temperature functions u(x, t) in ℝn+1 = {(x, t)| x ∈ ℝn,t > 0} are characterised by

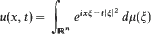
where μ is a positive measure satisfying that for every ℰ > 0,

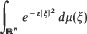
is finite. A transform 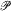is introduced to give an isomorphism between the class ofall positive definite temperature functions and the class of all possible temperature functions in 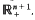Then correspondence given by 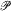generalises the Bochner–Schwartz Theorem for the Schwartz distributions and extends Widder's correspondence characterising some subclass of the positive temperature functions by the Fourier-Stieltjes transform.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 127 , Issue 5 , 1997 , pp. 947 - 961
Copyright
Copyright © Royal Society of Edinburgh 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Aronszajn, N.. Traces of analytic solutions of the heat equations. Astérisque 2–3 (1973), 5–68.Google Scholar
2Bochner, S.. Lecture on Fourier integral (Princeton: Princeton University Press, 1959).Google Scholar
3Chung, J., Chung, S. Y. and Kim, D.. Une caractérisation de l'espace de Schwartz. C. R. Acad. Sci. Paris Sér. I Math. 316 (1993), 23–5.Google Scholar
4Chung, J., Chung, S. Y. and Kim, D.. A characterization for Fourier hyperfunctions. Publ. Res. Inst. Math. Sci. 30 (1994), 203–8.Google Scholar
5Chung, J., Chung, S. Y. and Kim, D.. Positive definite hyperfunctions. Nagoya Math. J 140 (1995), 139–49.Google Scholar
6Chung, S.-Y. and Kim, D.. Distributions with exponential growth and Bochner—Schwartz theorem for Fourier hyperfunctions. Publ. Res. Inst. Sci. 31 (1995), 829–45.CrossRefGoogle Scholar
7Chung, J., Chung, S. Y. and Kim, D.. Uniqueness for the Cauchy problem of the heat equation without uniform conditions on time. J. Korean Math. Soc. 31 (1994), 245–54.Google Scholar
8Chung, J., Chung, S. Y. and Kim, D.. An example of nonuniqueness of Cauchy problem for theheat equation. Comm. Partial Differential Equations 19 (1994), 1257–61.CrossRefGoogle Scholar
9Gelfand, I. M. and Shilov, G. E.. Generalized functions II, III (New York: Academic Press, 1967).Google Scholar
10Gelfand, I. M. and Vilenkin, N. Y.. Generalized functions IV (New York: Academic Press, 1968).Google Scholar
11Haimo, D. T.. Generalized temperature functions. Duke Math. J. 33 (1966), 305–22.Google Scholar
12Haimo, D. T.. Widder temperature representations. J. Math. Anal. Appl. 41 (1973), 170–8.Google Scholar
13Johnson, G.. Harmonic functions on the unit disk. Illinois J. Math. 12 (1968), 366–85.Google Scholar
14Kaneko, A.. Introduction to hyperfunctions (Tokyo: KTK Sci. Publ., 1988).Google Scholar
15Kim, K. H., Chung, S.-Y. and Kim, D.. Fourier hyperfunctions as the boundary values of smooth solutions of heat equations. Publ. Res. Inst. Math. Sci. 29 (1993), 289–300.Google Scholar
16Matsuzawa, T.. A calculus approach to hyperfunctions II. Trans. Amer. Math. Soc. 313 (1990), 619–54.CrossRefGoogle Scholar
17Moser, J.. A Harnack type inequality for parabolic differential equations. Comm. Pure Appl. Math. 17 (1964), 101–34.Google Scholar
18Schwartz, L.. Theorie des distributions (Paris: Hermann, 1966).Google Scholar
19Widder, D. V.. Positive solution of heat equations. Bull. Amer. Math. Soc. 69 (1963), 111–12.Google Scholar
20Widder, D. V.. The role of Apell transformation in the theory of heat conduction. Trans. Amer. Math. Soc. 109 (1963), 121–34.Google Scholar
21Widder, D. V.. Some analogies from classical analysis in the theory of heat conduction. Arch. Rational Mech. Anal. 21 (1966), 108–19.Google Scholar
22Widder, D. V.. The heat equation (New York: Academic Press, 1975).Google Scholar
23Zayed, A.. Hyperfunctions as boundary values of generalized axially symmetric potentials. Illinois J. Math. 25 (1981), 306–17.Google Scholar
24Zayed, A.. Laguerre series as boundary values. SIAM J. Math. Anal. 13 (1982), 263–79.CrossRefGoogle Scholar