Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-19T17:22:02.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximal smoothness of solutions to certain Euler–Lagrange equations from nonlinear elasticity

Published online by Cambridge University Press:  14 November 2011

Patricia Bauman ,
Daniel Phillips  and
Nicholas C. Owen
Patricia Bauman
Affiliation:
Department of Mathematics, Purdue University, West Lafayette, IN. 47907, U.S.A.
Daniel Phillips
Affiliation:
Department of Mathematics, Purdue University, West Lafayette, IN. 47907, U.S.A.
Nicholas C. Owen
Affiliation:
Department of Applied and Computational Mathematics, The University of Sheffield, Sheffield, S10 2TN, England
Get access Rights & Permissions [Opens in a new window]

Synopsis

We investigate the maximal smoothness of stationary states for the multiple integral =

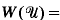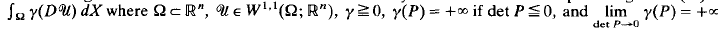
Such variational problems are motivated by the study of nonlinear elasticity. Assuming certain structure conditions for γ and given a stationary state , we derive an a priori LP estimate for 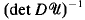for any p < ∞ in terms of 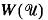and 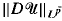where 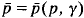. As a consequence, we show that a C1,β stationary state necessarily satisfies det 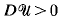and is of class C2, β in Ω. Nevertheless, singular stationary states do exist: we construct a nonsmooth C1 solution for a particular γ in two dimensions such that det 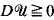in Ω and det vanishes at precisely one point in Ω.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 119 , Issue 3-4 , 1991 , pp. 241 - 263
Copyright
Copyright © Royal Society of Edinburgh 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Acerbi, E. and Fusco, N.. Semicontinuity problems in the calculus of variations. Arch. Rational Mech. Anal. 86 (1984), 125–145.Google Scholar
2Ball, J. M.. Convexity conditions and existence theorems in nonlinear elasticity. Arch. Rational Mech. Anal. 63 (1977), 337–403.Google Scholar
3Ball, J. M.. Constitutive inequalities and existence theorems in nonlinear elastostatics. In Nonlinear Analysis and Mechanics: Heriot-Watt Symposium, Vol. I, ed. Knops, R. J. (London: Pitman, 1977).Google Scholar
4Ball, J. M.. Global invertibility of Sobolev functions and the interpenetration of matter. Proc. Roy. Soc. Edinburgh Sect. A 88 (1981), 315–328.CrossRefGoogle Scholar
5Ball, J. M.. Discontinuous equilibrium solutions and cavitation in nonlinear elasticity. Philos. Trans. Roy. Soc. London Ser. A 306 (1982), 557–611.Google Scholar
6Ball, J. M.. Minimizers and the Euler–Lagrange equations. Proc. of ISIMM Conf. (Paris: Springer, 1983).Google Scholar
7Ball, J. M. and Murat, F.. W1,p-quasiconvexity and variational problems for multiple integrals. J. Fund. Anal. 58 (1984), 225–253.Google Scholar
8Bauman, P., Owen, N. C. and Phillips, D.. Maximum principles and a priori estimates for a class of problems in nonlinear elasticity. Ann. Inst. H. Poincaré: Anal. Non Linéaire 8 (1991), 119–157.Google Scholar
9Ciarlet, P. G.. Mathematical Elasticity, Studies in Mathematics and its Applications 20 (New York: North-Holland, 1988).Google Scholar
10Dacorogna, B.. Direct Methods in the Calculus of Variations, Applied Mathematical Sciences 78, (Berlin: Springer, 1989).Google Scholar
11Giaquinta, M.. Multiple Integrals in the Calculus of Variations and Nonlinear Elliptic Systems, Annals of Mathematics Studies (Princeton, New Jersey: Princeton University Press, 1983).Google Scholar
12Ogden, R. W.. Large-deformation isotropic elasticity: on the correlation of theory and experiment for compressible rubberlike solids. Proc. Roy. Soc. London Ser. A 328 (1972), 567–583.Google Scholar
13Šverak, V.. Regularity properties of deformations with finite energy. Arch. Rational Mech. Anal. 100 (1988), 105–127.CrossRefGoogle Scholar
14Valent, T.. Boundary Value Problems of Finite Elasticity (Heidelberg: Springer, 1988).CrossRefGoogle Scholar