Article contents
Integral representation of functionals defined on curves of W1,p
Published online by Cambridge University Press: 14 November 2011
Abstract
Let I ⊂ ℝ be a bounded open interval, 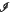 (I) be the family of all open subintervals of I and let p > 1. The aim of this paper is to give an integral representation result for abstract functionals F: W1,p(I;ℝn) ×
(I) be the family of all open subintervals of I and let p > 1. The aim of this paper is to give an integral representation result for abstract functionals F: W1,p(I;ℝn) × 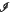 (I) → [0, + ∞) which are lower semicontinuous and satisfy suitable properties. In particular, we prove an integral representation theorem for the Г-limit of a sequence {Fh}h, of functionals of the form
(I) → [0, + ∞) which are lower semicontinuous and satisfy suitable properties. In particular, we prove an integral representation theorem for the Г-limit of a sequence {Fh}h, of functionals of the form
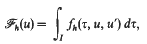
where each fh is a Borel function satisfying proper growth conditions.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 128 , Issue 2 , 1998 , pp. 193 - 217
- Copyright
- Copyright © Royal Society of Edinburgh 1998
References
- 3
- Cited by


