Hostname: page-component-848d4c4894-sjtt6 Total loading time: 0 Render date: 2024-06-20T03:45:16.409Z Has data issue: false hasContentIssue false
  • English
  • Français

An n-dimensional chemotaxis system with signal-dependent motility and generalized logistic source: global existence and asymptotic stabilization

Part of: Physiological, cellular and medical topics Partial differential equations Parabolic equations and systems

Published online by Cambridge University Press:  29 May 2020

Wenbin Lv  and
Qingyuan Wang
Wenbin Lv*
Affiliation:
School of Mathematical Sciences, Shanxi University, Taiyuan030006, China (lvwenbin@sxu.edu.cn)
Qingyuan Wang
Affiliation:
School of Mathematical Sciences, Shanxi University, Taiyuan030006, China (lvwenbin@sxu.edu.cn)
*
*Corresponding author
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper deals with the global existence for a class of Keller–Segel model with signal-dependent motility and general logistic term under homogeneous Neumann boundary conditions in a higher-dimensional smoothly bounded domain, which can be written as

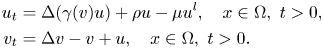$$\eqalign{& u_t = \Delta (\gamma (v)u) + \rho u-\mu u^l,\quad x\in \Omega ,\;t > 0, \cr & v_t = \Delta v-v + u,\quad x\in \Omega ,\;t > 0.} $$
It is shown that whenever ρ ∈ ℝ, μ > 0 and
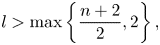$$l > \max \left\{ {\displaystyle{{n + 2} \over 2},2} \right\},$$
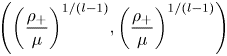then the considered system possesses a global classical solution for all sufficiently smooth initial data. Furthermore, the solution converges to the equilibrium
$$\left( {{\left( {\displaystyle{{\rho _ + } \over \mu }} \right)}^{1/(l-1)},{\left( {\displaystyle{{\rho _ + } \over \mu }} \right)}^{1/(l-1)}} \right)$$
as t → ∞ under some extra hypotheses, where ρ+ = max{ρ, 0}.

Keywords

Global existenceBoundednessLarge time behaviourSignal-dependent motility

MSC classification

Primary: 35A01: Existence problems
Secondary: 35B45: A priori estimates 35K51: Initial-boundary value problems for second-order parabolic systems 92C17: Cell movement (chemotaxis, etc.)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 2 , April 2021 , pp. 821 - 841
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Alikakos, N. D.. L p bounds of solutions of reaction-diffusion equations. Comm. Partial Differ. Eq. 4 (1979), 827–868.CrossRefGoogle Scholar
2Amann, H., Nonhomogeneous linear and quasilinear elliptic and parabolic boundary value problems. In Function spaces, differential operators and nonlinear analysis (Friedrichroda, 1992), volume 133 of Teubner-Texte Math., pages 9–126. Teubner, Stuttgart, 1993.CrossRefGoogle Scholar
3Cao, X. R.. Large time behavior in the logistic Keller-Segel model via maximal Sobolev regularity. Discrete Contin. Dyn. Syst. Ser. B 22 (2017), 3369–3378.Google Scholar
4Hillen, T. and Painter, K. J.. A user's guide to PDE models for chemotaxis. J. Math. Biol. 58 (2009), 183–217.CrossRefGoogle ScholarPubMed
5Horstmann, D.. From 1970 until present: the Keller-Segel model in chemotaxis and its consequences. I. Jahresber. Deutsch. Math.-Verein. 105 (2003), 103–165.Google Scholar
6Jin, H. Y., Kim, Y. J. and Wang, Z. A.. Boundedness, stabilization, and pattern formation driven by density-suppressed motility. SIAM J. Appl. Math. 78 (2018), 1632–1657.CrossRefGoogle Scholar
7Keller, E. F. and Segel, L. A.. Initiation of slime mold aggregation viewed as an instability. J. Theoret. Biol. 26 (1970), 399–415.CrossRefGoogle ScholarPubMed
8Lankeit, J.. Eventual smoothness and asymptotics in a three-dimensional chemotaxis system with logistic source. J. Differ. Equ. 258 (2015), 1158–1191.CrossRefGoogle Scholar
9Liu, Z. R. and Xu, J.. Large time behavior of solutions for density-suppressed motility system in higher dimensions. J. Math. Anal. Appl. 475 (2019), 1596–1613.CrossRefGoogle Scholar
10Lv, W. B., Global existence for a class of chemotaxis-consumption systems with signal-dependent motility and generalized logistic source. Nonlinear Anal. Real World Appl. 56 (2020), 103160.CrossRefGoogle Scholar
11Lv, W. B. and Wang, Q.. A chemotaxis system with signal-dependent motility, indirect signal production and generalized logistic source: global existence and asymptotic stabilization. J. Math. Anal. Appl. 488 (2020), 124108.CrossRefGoogle Scholar
12Lv, W. B. and Wang, Q. Y.. Global existence for a class of keller-segel models with signal-dependent motility and general logistic term. Evol. Equ. Control (2020) http://dx.doi.org/10.3934/eect.2020040.Google Scholar
13Lv, W. B. and Wang, Q. Y.. Global existence for a class of chemotaxis systems with signal-dependent motility, indirect signal production and generalized logistic source. Z. Angew. Math. Phys. 71 (2020), 53.CrossRefGoogle Scholar
14Porzio, M. M. and Vespri, V.. Hölder estimates for local solutions of some doubly nonlinear degenerate parabolic equations. J. Differ. Eq. 103 (1993), 146–178.CrossRefGoogle Scholar
15Suzuki, T. 2005 Free energy and self-interacting particles. 62 Progress in Nonlinear Differential Equations and their Applications. Boston, MA: Birkhäuser Boston Inc..CrossRefGoogle Scholar
16Suzuki, T. 2018 Chemotaxis, reaction, network. Mathematics for self-organization. Hackensack, NJ: World Scientific Publishing Co. Pte. Ltd..CrossRefGoogle Scholar
17Tao, Y. S. and Winkler, M.. A chemotaxis-haptotaxis model: the roles of nonlinear diffusion and logistic source. SIAM J. Math. Anal. 43 (2011), 685–704.CrossRefGoogle Scholar
18Tao, Y. S. and Winkler, M.. Boundedness in a quasilinear parabolic-parabolic Keller-Segel system with subcritical sensitivity. J. Differ. Eq. 252 (2012), 692–715.CrossRefGoogle Scholar
19Tao, Y. S. and Winkler, M.. Large time behavior in a multidimensional chemotaxis-haptotaxis model with slow signal diffusion. SIAM J. Math. Anal. 47 (2015), 4229–4250.CrossRefGoogle Scholar
20Tao, Y. S. and Winkler, M.. Blow-up prevention by quadratic degradation in a two-dimensional Keller-Segel-Navier-Stokes system. Z. Angew. Math. Phys. 67 (2016), 138.CrossRefGoogle Scholar
21Tao, Y. S. and Winkler, M.. Effects of signal-dependent motilities in a Keller-Segel-type reaction-diffusion system. Math. Models Methods Appl. Sci. 27 (2017), 1645–1683.CrossRefGoogle Scholar
22Tello, J. I. and Winkler, M.. A chemotaxis system with logistic source. Comm. Partial Differ. Eq. 32 (2007), 849–877.CrossRefGoogle Scholar
23Wang, J. P. and Wang, M. X.. Boundedness in the higher-dimensional Keller-Segel model with signal-dependent motility and logistic growth. J. Math. Phys. 60 (2019), 011507.CrossRefGoogle Scholar
24Winkler, M.. Chemotaxis with logistic source: very weak global solutions and their boundedness properties. J. Math. Anal. Appl. 348 (2008), 708–729.CrossRefGoogle Scholar
25Winkler, M.. Aggregation vs. global diffusive behavior in the higher-dimensional Keller-Segel model. J. Differ. Eq. 248 (2010), 2889–2905.CrossRefGoogle Scholar
26Winkler, M.. Boundedness in the higher-dimensional parabolic-parabolic chemotaxis system with logistic source. Comm. Partial Differ. Eq. 35 (2010), 1516–1537.CrossRefGoogle Scholar
27Winkler, M.. Blow-up in a higher-dimensional chemotaxis system despite logistic growth restriction. J. Math. Anal. Appl. 384 (2011), 261–272.CrossRefGoogle Scholar
28Winkler, M.. Global solutions in a fully parabolic chemotaxis system with singular sensitivity. Math. Methods Appl. Sci. 34 (2011), 176–190.CrossRefGoogle Scholar
29Winkler, M.. Finite-time blow-up in the higher-dimensional parabolic-parabolic Keller-Segel system. J. Math. Pures Appl. 100 (2013), 748–767.CrossRefGoogle Scholar
30Winkler, M.. Global asymptotic stability of constant equilibria in a fully parabolic chemotaxis system with strong logistic dampening. J. Differ. Eq. 257 (2014), 1056–1077.CrossRefGoogle Scholar
31Winkler, M.. How far can chemotactic cross-diffusion enforce exceeding carrying capacities? J. Nonlinear Sci. 24 (2014), 809–855.CrossRefGoogle Scholar
32Winkler, M.. Emergence of large population densities despite logistic growth restrictions in fully parabolic chemotaxis systems. Discrete Contin. Dyn. Syst. Ser. B 22 (2017), 2777–2793.Google Scholar
33Winkler, M.. Finite-time blow-up in low-dimensional Keller-Segel systems with logistic-type superlinear degradation. Z. Angew. Math. Phys. 69 (2018), 40.CrossRefGoogle Scholar
34Winkler, M.. A three-dimensional Keller-Segel-Navier-Stokes system with logistic source: global weak solutions and asymptotic stabilization. J. Funct. Anal. 276 (2019), 1339–1401.CrossRefGoogle Scholar
35Xiang, T.. Sub-logistic source can prevent blow-up in the 2D minimal Keller-Segel chemotaxis system. J. Math. Phys. 59 (2018), 081502.CrossRefGoogle Scholar
36Yoon, C. and Kim, Y. J.. Global existence and aggregation in a Keller-Segel model with Fokker-Planck diffusion. Acta Appl. Math. 149 (2017), 101–123.CrossRefGoogle Scholar