Article contents
On the generalized Hardy-Rellich inequalities
Published online by Cambridge University Press: 26 January 2019
Abstract
In this paper, we look for the weight functions (say g) that admit the following generalized Hardy-Rellich type inequality:
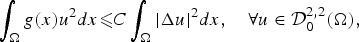 $$\int_\Omega g (x)u^2 dx \les C\int_\Omega \vert \Delta u \vert ^2 dx,\quad \forall u\in {\rm {\cal D}}_0^{2,2} (\Omega ),$$
$$\int_\Omega g (x)u^2 dx \les C\int_\Omega \vert \Delta u \vert ^2 dx,\quad \forall u\in {\rm {\cal D}}_0^{2,2} (\Omega ),$$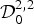 ${\cal D}_0^{2,2} $ into certain Lorentz-Zygmund spaces proved by Hansson and later by Brezis and Wainger.
${\cal D}_0^{2,2} $ into certain Lorentz-Zygmund spaces proved by Hansson and later by Brezis and Wainger.
Keywords
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 2 , April 2020 , pp. 897 - 919
- Copyright
- Copyright © Royal Society of Edinburgh 2019
References
- 3
- Cited by


