Article contents
Generalized small cancellation conditions, non-positive curvature and diagrammatic reducibility
Published online by Cambridge University Press: 02 March 2021
Abstract
We present a metric condition 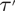 $\TTMetric$ which describes the geometry of classical small cancellation groups and applies also to other known classes of groups such as two-dimensional Artin groups. We prove that presentations satisfying condition
$\TTMetric$ which describes the geometry of classical small cancellation groups and applies also to other known classes of groups such as two-dimensional Artin groups. We prove that presentations satisfying condition 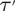 $\TTMetric$ are diagrammatically reducible in the sense of Sieradski and Gersten. In particular, we deduce that the standard presentation of an Artin group is aspherical if and only if it is diagrammatically reducible. We show that, under some extra hypotheses,
$\TTMetric$ are diagrammatically reducible in the sense of Sieradski and Gersten. In particular, we deduce that the standard presentation of an Artin group is aspherical if and only if it is diagrammatically reducible. We show that, under some extra hypotheses, 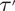 $\TTMetric$-groups have quadratic Dehn functions and solvable conjugacy problem. In the spirit of Greendlinger's lemma, we prove that if a presentation P = 〈X| R〉 of group G satisfies conditions
$\TTMetric$-groups have quadratic Dehn functions and solvable conjugacy problem. In the spirit of Greendlinger's lemma, we prove that if a presentation P = 〈X| R〉 of group G satisfies conditions 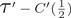 $\TTMetric -C'(\frac {1}{2})$, the length of any nontrivial word in the free group generated by X representing the trivial element in G is at least that of the shortest relator. We also introduce a strict metric condition
$\TTMetric -C'(\frac {1}{2})$, the length of any nontrivial word in the free group generated by X representing the trivial element in G is at least that of the shortest relator. We also introduce a strict metric condition 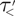 $\TTMetricStrict$, which implies hyperbolicity.
$\TTMetricStrict$, which implies hyperbolicity.
Keywords
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 3 , June 2022 , pp. 545 - 566
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
- 1
- Cited by



