Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Song, Yueqiang
Zhao, Fu
Pu, Hongling
and
Shi, Shaoyun
2020.
Existence results for Kirchhoff equations with Hardy–Littlewood–Sobolev critical nonlinearity.
Nonlinear Analysis,
Vol. 198,
Issue. ,
p.
111900.
Gao, Fashun
Yang, Minbo
and
Zhou, Jiazheng
2020.
Existence of multiple semiclassical solutions for a critical Choquard equation with indefinite potential.
Nonlinear Analysis,
Vol. 195,
Issue. ,
p.
111817.
Liang, Sihua
Wen, Lixi
and
Zhang, Binlin
2020.
Solutions for a class of quasilinear Choquard equations with Hardy–Littlewood–Sobolev critical nonlinearity.
Nonlinear Analysis,
Vol. 198,
Issue. ,
p.
111888.
Liang, Sihua
Pucci, Patrizia
and
Zhang, Binlin
2020.
Multiple solutions for critical Choquard-Kirchhoff type equations.
Advances in Nonlinear Analysis,
Vol. 10,
Issue. 1,
p.
400.
Wang, Wenbo
Zhou, Jianwen
and
Li, Yongkun
2020.
On the Ground State to Hamiltonian Elliptic System with Choquard’s Nonlinear Term.
Advances in Mathematical Physics,
Vol. 2020,
Issue. ,
p.
1.
Giacomoni, Jacques
Wei, Yuanhong
and
Yang, Minbo
2020.
Nondegeneracy of solutions for a critical Hartree equation.
Nonlinear Analysis,
Vol. 199,
Issue. ,
p.
111969.
Chen, Peng
and
Liu, Xiaochun
2021.
Positive solutions for Choquard equation in exterior domains.
Communications on Pure & Applied Analysis,
Vol. 20,
Issue. 6,
p.
2237.
Gao, Fashun
Liu, Haidong
Moroz, Vitaly
and
Yang, Minbo
2021.
High energy positive solutions for a coupled Hartree system with Hardy-Littlewood-Sobolev critical exponents.
Journal of Differential Equations,
Vol. 287,
Issue. ,
p.
329.
Cui, Ying-Xin
2021.
On nodal solutions of the fractional Choquard equation.
Journal of Mathematical Analysis and Applications,
Vol. 500,
Issue. 2,
p.
125152.
Luo, Xiaorong
Mao, Anmin
and
Sang, Yanbin
2021.
Nonlinear Choquard equations with Hardy-Littlewood-Sobolev critical exponents.
Communications on Pure & Applied Analysis,
Vol. 20,
Issue. 4,
p.
1319.
Yang, Minbo
Zhao, Fukun
and
Zhao, Shunneng
2021.
Classification of solutions to a nonlocal equation with doubly Hardy-Littlewood-Sobolev critical exponents.
Discrete & Continuous Dynamical Systems,
Vol. 41,
Issue. 11,
p.
5209.
He, Rui
and
Liu, Xiangqing
2021.
Localized nodal solutions for semiclassical Choquard equations.
Journal of Mathematical Physics,
Vol. 62,
Issue. 9,
Zheng, Yu
Gao, Fashun
Shen, Zifei
and
Yang, Minbo
2021.
On a class of coupled critical Hartree system with deepening potential.
Mathematical Methods in the Applied Sciences,
Vol. 44,
Issue. 1,
p.
772.
Gao, Fashun
Rădulescu, Vicentiu D.
Yang, Minbo
and
Zheng, Yu
2021.
Standing waves for the pseudo-relativistic Hartree equation with Berestycki-Lions nonlinearity.
Journal of Differential Equations,
Vol. 295,
Issue. ,
p.
70.
Yang, Minbo
and
Zhou, Xianmei
2021.
On a Coupled Schrödinger System with Stein–Weiss Type Convolution Part.
The Journal of Geometric Analysis,
Vol. 31,
Issue. 10,
p.
10263.
Li, Rui
and
Song, Yueqiang
2021.
Multiple solutions for a quasilinear Choquard equation with critical nonlinearity.
Open Mathematics,
Vol. 19,
Issue. 1,
p.
1684.
Alves, Claudianor O.
Figueiredo, Giovany M.
and
Molle, Riccardo
2021.
Multiple positive bound state solutions for a critical Choquard equation.
Discrete & Continuous Dynamical Systems,
Vol. 41,
Issue. 10,
p.
4887.
Yang, Xiaolong
2021.
Bound state solutions of fractional Choquard equation with Hardy–Littlewood–Sobolev critical exponent.
Computational and Applied Mathematics,
Vol. 40,
Issue. 5,
Shen, Zifei
Yang, Minbo
and
Zhao, Shunneng
2021.
Existence of solutions for a weakly coupled Schrödinger system with critical growth.
Mathematical Methods in the Applied Sciences,
Vol. 44,
Issue. 17,
p.
13376.
Zhou, Fen
and
Shen, Zifei
2021.
Existence of a radial solution to a 1-Laplacian problem in RN.
Applied Mathematics Letters,
Vol. 118,
Issue. ,
p.
107138.
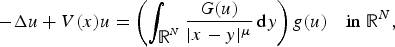 $$-\Delta u + V(x)u = \left( {\int_{{\open R}^N} {\displaystyle{{G(u)} \over { \vert x-y \vert ^\mu }}} \,{\rm d}y} \right)g(u)\quad {\rm in}\;{\open R}^N, $$
$$-\Delta u + V(x)u = \left( {\int_{{\open R}^N} {\displaystyle{{G(u)} \over { \vert x-y \vert ^\mu }}} \,{\rm d}y} \right)g(u)\quad {\rm in}\;{\open R}^N, $$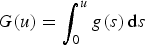 $G(u)=\int ^u_0g(s)\,{\rm d}s$. Firstly, by assuming that the potential V(x) might be sign-changing, we study the existence of Mountain-Pass solution via a nonlocal version of the second concentration- compactness principle. Secondly, under the conditions introduced by Benci and Cerami , we also study the existence of high energy solution by using a nonlocal version of global compactness lemma.
$G(u)=\int ^u_0g(s)\,{\rm d}s$. Firstly, by assuming that the potential V(x) might be sign-changing, we study the existence of Mountain-Pass solution via a nonlocal version of the second concentration- compactness principle. Secondly, under the conditions introduced by Benci and Cerami , we also study the existence of high energy solution by using a nonlocal version of global compactness lemma.

