Existence of semiclassical ground-state solutions for semilinear elliptic systems
Published online by Cambridge University Press: 10 August 2012
Abstract
This paper is concerned with the following semilinear elliptic equations of the form
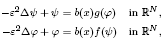
where ε is a small positive parameter, and where f and g denote superlinear and subcritical nonlinearity. Suppose that b(x) has at least one maximum. We prove that the system has a ground-state solution (ψε, φε) for all sufficiently small ε > 0. Moreover, we show that (ψε, φε) converges to the ground-state solution of the associated limit problem and concentrates to a maxima point of b(x) in certain sense, as ε → 0. Furthermore, we obtain sufficient conditions for nonexistence of ground-state solutions.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 142 , Issue 4 , August 2012 , pp. 867 - 895
- Copyright
- Copyright © Royal Society of Edinburgh 2012
- 7
- Cited by


