Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Goodrich, Christopher S.
2021.
Nonlocal Differential Equations with Convolution Coefficients and Applications to Fractional Calculus.
Advanced Nonlinear Studies,
Vol. 21,
Issue. 4,
p.
767.
Goodrich, Christopher S.
2021.
Discrete Kirchhoff equations with sign-changing coefficients.
Journal of Difference Equations and Applications,
Vol. 27,
Issue. 5,
p.
664.
Goodrich, Christopher S.
2021.
Topological analysis of doubly nonlocal boundary value problems.
Journal of Fixed Point Theory and Applications,
Vol. 23,
Issue. 2,
Goodrich, Christopher S.
2021.
A one-dimensional Kirchhoff equation with generalized convolution coefficients.
Journal of Fixed Point Theory and Applications,
Vol. 23,
Issue. 4,
Goodrich, Christopher
2021.
A topological approach to a class of one-dimensional Kirchhoff equations.
Proceedings of the American Mathematical Society, Series B,
Vol. 8,
Issue. 14,
p.
158.
Goodrich, Christopher S.
2021.
Nonlocal differential equations with concave coefficients of convolution type.
Nonlinear Analysis,
Vol. 211,
Issue. ,
p.
112437.
Goodrich, Christopher
2022.
Nonexistence and parameter range estimates for convolution differential equations.
Proceedings of the American Mathematical Society, Series B,
Vol. 9,
Issue. 24,
p.
254.
Goodrich, Christopher S.
2022.
An analysis of nonlocal difference equations with finite convolution coefficients.
Journal of Fixed Point Theory and Applications,
Vol. 24,
Issue. 1,
Goodrich, Christopher S.
2023.
Nonlocal differential equations with convex convolution coefficients.
Journal of Fixed Point Theory and Applications,
Vol. 25,
Issue. 1,
Goodrich, Christopher S.
2023.
Nonlocal differential equations with (p,q)$ {(p,q)}$ growth.
Bulletin of the London Mathematical Society,
Vol. 55,
Issue. 3,
p.
1373.
Goodrich, Christopher S.
2024.
An application of Sobolev's inequality to one-dimensional Kirchhoff equations.
Journal of Differential Equations,
Vol. 385,
Issue. ,
p.
463.
Wei, Jia-Li
Wu, Guo-Cheng
and
Lozi, René
2024.
RIGHT HADAMARD FRACTIONAL DIFFERENCES AND SUMMATION BY PARTS.
Rocky Mountain Journal of Mathematics,
Vol. 54,
Issue. 3,
Hao, Xinan
and
Wang, Xuhui
2024.
Positive solutions of parameter-dependent nonlocal differential equations with convolution coefficients.
Applied Mathematics Letters,
Vol. 153,
Issue. ,
p.
109063.
Goodrich, Christopher S.
2024.
A surprising property of nonlocal operators: the deregularising effect of nonlocal elements in convolution differential equations.
Advanced Nonlinear Studies,
Bellamouchi, Chahinez
and
Zaouche, Elmehdi
2024.
Positive solutions, positive radial solutions and uniqueness results for some nonlocal elliptic problems.
Journal of Elliptic and Parabolic Equations,
Vol. 10,
Issue. 1,
p.
279.
Zhu, Tao
2024.
BOUNDEDNESS, MONOTONICITY AND ASYMPTOTIC BEHAVIOR OF SOLUTIONS OF CAPUTO FRACTIONAL DIFFERENTIAL EQUATIONS.
Journal of Integral Equations and Applications,
Vol. 36,
Issue. 2,
Goodrich, Christopher
2024.
Nonexistence of nontrivial solutions to Kirchhoff-like equations.
Proceedings of the American Mathematical Society, Series B,
Vol. 11,
Issue. 28,
p.
304.
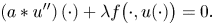 \begin{equation} \left(a*u''\right)(\cdot)+\lambda f\big(\cdot,u(\cdot)\big)=0.\nonumber \end{equation}
\begin{equation} \left(a*u''\right)(\cdot)+\lambda f\big(\cdot,u(\cdot)\big)=0.\nonumber \end{equation}


