Composite meromorphic functions and normal families
Published online by Cambridge University Press: 13 March 2009
Abstract
We study the normality of families of meromorphic functions defined in terms of certain omitted functions. In particular, we prove the following results. Firstly, if 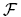 is a family of meromorphic functions in a domain D ⊂ ℂ, and a(z), b(z) and c(z) are distinct meromorphic functions in D and if, for all f ∈
is a family of meromorphic functions in a domain D ⊂ ℂ, and a(z), b(z) and c(z) are distinct meromorphic functions in D and if, for all f ∈ 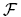 and all z ∈ D, f(z) ≠ a(z), f(z) ≠ b(z) and f(z) ≠ c(z), then
and all z ∈ D, f(z) ≠ a(z), f(z) ≠ b(z) and f(z) ≠ c(z), then 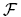 is normal in D. Secondly, letting R(w) be a rational function of degree greater than or equal to 3 and
is normal in D. Secondly, letting R(w) be a rational function of degree greater than or equal to 3 and 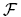 be a family of functions meromorphic in a domain D ⊂ ℂ, if there exists a non-constant meromorphic function α(z) in D such that, for all f ∈
be a family of functions meromorphic in a domain D ⊂ ℂ, if there exists a non-constant meromorphic function α(z) in D such that, for all f ∈ 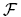 and z ∈ D, R(f(z)) ≠ α(z), then
and z ∈ D, R(f(z)) ≠ α(z), then 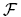 is normal in D.
is normal in D.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 139 , Issue 1 , February 2009 , pp. 57 - 72
- Copyright
- Copyright © Royal Society of Edinburgh 2009
- 10
- Cited by


