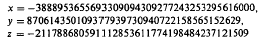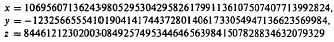Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dofs, Erik
1998.
Unsolvable Cases of $P^3+Q^3+cR^3=dPQR$.
Rocky Mountain Journal of Mathematics,
Vol. 28,
Issue. 3,
Tho, Nguyen Xuan
2022.
On a Diophantine Equation.
Vietnam Journal of Mathematics,
Vol. 50,
Issue. 1,
p.
183.
THO, NGUYEN XUAN
2022.
ON A PROBLEM OF RICHARD GUY.
Bulletin of the Australian Mathematical Society,
Vol. 105,
Issue. 1,
p.
12.
Tho, Nguyen Xuan
2022.
On a remark of Sierpínski.
Rocky Mountain Journal of Mathematics,
Vol. 52,
Issue. 2,
Tho, Nguyen Xuan
2022.
On Sums of Positive Rationals with Given Products.
Mediterranean Journal of Mathematics,
Vol. 19,
Issue. 4,
Falconer, Kenneth J.
2022.
Richard Kenneth Guy, 1916–2020.
Bulletin of the London Mathematical Society,
Vol. 54,
Issue. 1,
p.
318.
Garaev, M. Z.
2023.
On integer values of sum and product of three positive rational numbers.
Periodica Mathematica Hungarica,
Vol. 87,
Issue. 2,
p.
484.