No CrossRef data available.
Article contents
Theorems Relating to Quadratic Forms and their Discriminant Matrices
Published online by Cambridge University Press: 20 January 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In a paper read before the Research Branch of the Royal Statistical Society (Ref. 1, p. 150) the following case was considered:
Let the expression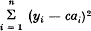 
be given; introduce, for c, a linear form in 
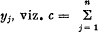and obtain
If the yi are sample values from a normal population with unit variance, then it is known (Ref. 2) that (1) is distributed as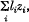 
where zi varies as chi-squared with one degree of freedom and the li are the latent roots of the matrix of the quadratic form. If these latent roots are f times unity and n—f times zero, then this reduces to a chi-squared distribution with f degrees of freedom.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 10 , Issue 1 , January 1953 , pp. 13 - 15
- Copyright
- Copyright © Edinburgh Mathematical Society 1953
References
REFERENCES
1.Vajda, S.. “Statistical investigation of casualties suffered by certain types of vessels,” Supp. J. JR. S. S., 9 (1947), 141.Google Scholar
2.Cochran, W. G., “The distribution of quadratic forms in a normal system,” Proc. Camb. Phil. Soc., 30(1934), 178.CrossRefGoogle Scholar
3.Aitken, A. C., “On least squares and linear combinations of observations,” Proc. Boy. Soc. Edinburgh, 55 (1935), 42.CrossRefGoogle Scholar
You have
Access