No CrossRef data available.
Article contents
A Theorem on Alternants
Published online by Cambridge University Press: 20 January 2009
Extract
The following is a direct proof of a theorem by Zia-ud-Din.
Let {ν} ≡ {ν1, ν2, …, νp)} be any S-function of weight r + s such that
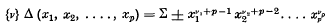
in the alternant denoted in the theorem by A(αβγ….). Let {μ} be an S-function of weight s, equal to 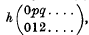 and let {λ} be an S-function of weight r, such that {λ}δ(x1, …,xp) is obtained with coefficient gλμν by diminishing the indices in the alternant {ν}δ(x1, …,xp) according to the theorem.
and let {λ} be an S-function of weight r, such that {λ}δ(x1, …,xp) is obtained with coefficient gλμν by diminishing the indices in the alternant {ν}δ(x1, …,xp) according to the theorem.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1936
References
page 261 note 1Proc. Edinburgh Math. Soc., 4 (1934), 51.Google Scholar
page 261 note 2Littlewood, D. E. and Richardson, A. R., Phil. Trans. Roy. Soc. (A), 233 (1934), 99.CrossRefGoogle Scholar


