Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-25T06:05:26.064Z Has data issue: false hasContentIssue false
  • English
  • Français

On the notions of upper and lower density

Part of: Classical measure theory Sequences and sets Probability theory on algebraic and topological structures

Published online by Cambridge University Press:  30 August 2019

Paolo Leonetti  and
Salvatore Tringali
Paolo Leonetti
Affiliation:
Department of Statistics, Università Luigi Bocconi, via Sarfatti 25, 20136 Milano, Italy (leonetti.paolo@gmail.com)
Salvatore Tringali
Affiliation:
Department of Mathematics, Texas A & M University at Qatar, PO Box 23874 Doha, Qatar (salvo.tringali@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 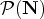$\mathcal {P}(\mathbf{N})$ be the power set of N. We say that a function 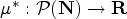$\mu ^\ast : \mathcal {P}(\mathbf{N}) \to \mathbf{R}$ is an upper density if, for all X, Y ⊆ N and h, k ∈ N+, the following hold: (f1) 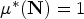$\mu ^\ast (\mathbf{N}) = 1$; (f2) 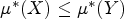$\mu ^\ast (X) \le \mu ^\ast (Y)$ if X ⊆ Y; (f3) $\mu ^\ast (X \cup Y) \le \mu ^\ast (X) + \mu ^\ast (Y)$; (f4) 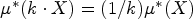$\mu ^\ast (k\cdot X) = ({1}/{k}) \mu ^\ast (X)$, where k · X : = {kx: x ∈ X}; and (f5) $\mu ^\ast (X + h) = \mu ^\ast (X)$. We show that the upper asymptotic, upper logarithmic, upper Banach, upper Buck, upper Pólya and upper analytic densities, together with all upper α-densities (with α a real parameter ≥ −1), are upper densities in the sense of our definition. Moreover, we establish the mutual independence of axioms (f1)–(f5), and we investigate various properties of upper densities (and related functions) under the assumption that (f2) is replaced by the weaker condition that 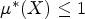$\mu ^\ast (X)\le 1$ for every X ⊆ N. Overall, this allows us to extend and generalize results so far independently derived for some of the classical upper densities mentioned above, thus introducing a certain amount of unification into the theory.

Keywords

analytic densityasymptotic (or natural) densityaxiomatizationBanach (or uniform) densityBuck densitylogarithmic densityPólya densityupper and lower densities

MSC classification

Primary: 11B05: Density, gaps, topology 28A10: Real- or complex-valued set functions 39B52: Equations for functions with more general domains and/or ranges
Secondary: 60B99: None of the above, but in this section
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 1 , February 2020 , pp. 139 - 167
Copyright
Copyright © Edinburgh Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

Current address: Institute of Analysis and Number Theory, Graz University of Technology, Kopernikusgasse 24/II, 8010 Graz, Austria.

†

Current address: College of Mathematics and Information Science, Hebei Normal University, Shijiazhuang, Hebei Province 050000, China.

References

1.Alexander, R., Density and multiplicative structure of sets of integers, Acta Arith. 12 (1967), 321–332.10.4064/aa-12-4-321-332CrossRefGoogle Scholar
2.Blass, A., Frankiewicz, R., Plebanek, G. and Ryll-Nardzewski, C., A note on extensions of asymptotic density, Proc. Amer. Math. Soc. 129(11) (2001), 3313–3320.CrossRefGoogle Scholar
3.Buck, R. C., The measure theoretic approach to density, Amer. J. Math. 68(4) (1946), 560–580.CrossRefGoogle Scholar
4.Buck, R. C., Generalized asymptotic density, Amer. J. Math. 75(2) (1953), 335–346.CrossRefGoogle Scholar
5.Di Nasso, M., Fine asymptotic densities for sets of natural numbers, Proc. Amer. Math. Soc. 138 (8) (2010), 2657–2665.10.1090/S0002-9939-10-10351-7CrossRefGoogle Scholar
6.Di Nasso, M. and Jin, R., Abstract density and ideal of sets, Acta Arith. 185(4) (2018), 301–313.CrossRefGoogle Scholar
7.Freedman, A. R. and Sember, J. J., Densities and summability, Pacific J. Math. 95(2) (1981), 293–305.10.2140/pjm.1981.95.293CrossRefGoogle Scholar
8.Fuchs, A. and Giuliano Antonini, R., Théorie générale des densités, Rend. Accad. Naz. Sci. XL Mem. Mat. 14(1) (1990), 253–294.Google Scholar
9.Gáliková, Z., László, B. and Šalát, T., Remarks on uniform density of sets of integers, Acta Acad. Paed. Agriensis, Sectio Mathematicae 29 (2002), 3–13.Google Scholar
10.Giuliano Antonini, R. and Grekos, G., Comparison between lower and upper α-densities and lower and upper α-analytic densities, Unif. Distrib. Theory 3(2) (2008), 21–35.Google Scholar
11.Grätzer, G., Lattice theory foundation (Birkhäuser, Basel, 2011).CrossRefGoogle Scholar
12.Green, B. and Tao, T., The primes contain arbitrarily long arithmetic progressions, Ann. of Math. 167(2) (2008), 481–547.10.4007/annals.2008.167.481CrossRefGoogle Scholar
13.Grekos, G., Sur la répartition des densités des sous-suites d'une suite d'entiers. PhD thesis, Université Pierre et Marie Curie, 1976 (in French).Google Scholar
14.Grekos, G., Répartition des densités des sous-suites d'une suite d'entiers, J. Number Theory 10(2) (1978), 177–191 (in French).CrossRefGoogle Scholar
15.Grekos, G., On various definitions of density (survey), Tatra Mt. Math. Publ. 31 (2005), 17–27.Google Scholar
16.Grekos, G., Mišík, L. and Tóth, J. T., Density sets of sets of positive integers, J. Number Theory 130(6) (2010), 1399–1407.CrossRefGoogle Scholar
17.Grekos, G., Toma, V. and Tomanová, J., A note on uniform or Banach density, Ann. Math. Blaise Pascal 17(1) (2010), 153–163.CrossRefGoogle Scholar
18.Halberstam, H. and Roth, K. F., Sequences, revised edn (Springer-Verlag, Berlin, 1983).10.1007/978-1-4613-8227-0CrossRefGoogle Scholar
19.Leonetti, P., Thinnable ideals and invariance of cluster points, Rocky Mountain J. Math. 48(6) (2018), 1951–1961.CrossRefGoogle Scholar
20.Leonetti, P. and Tringali, S., Upper and lower densities have the strong Darboux property, J. Number Theory 174 (2017), 445–455.CrossRefGoogle Scholar
21.Letavaj, P., Mišík, L. and Sleziak, M., Extreme points of the set of density measures, J. Math. Anal. Appl. 423(2) (2015), 1150–1165.CrossRefGoogle Scholar
22.Levinson, N., Gap and density theorems, Volume 26 (American Mathematical Society Colloquium Publications, New York, 1940).CrossRefGoogle Scholar
23.Liapounoff, A. A., Sur les fonctions-vecteurs complètement additives, Izv. Akad. Nauk SSSR Ser. Mat. 4(6) (1940), 465–478.Google Scholar
24.Luca, F., Porubský, Š., On asymptotic and logarithmic densities, Tatra Mt. Math. Publ. 31 (2005), 75–86.Google Scholar
25.Maharam, D., Finitely additive measures on the integers, Sankhyā Ser. A 38(1) (1976), 44–59.Google Scholar
26.Marinacci, M., An axiomatic approach to complete patience and time invariance, J. Econom. Theory 83(1) (1998), 105–144.CrossRefGoogle Scholar
27.Mekler, A. H., Finitely additive measures on N and the additive property, Proc. Amer. Math. Soc. 92(3) (1984), 439–444.Google Scholar
28.Niven, I., The asymptotic density of sequences, Bull. Amer. Math. Soc. 57(6) (1951), 420–434.CrossRefGoogle Scholar
29.Niven, I., Zuckerman, H. S. and Montgomery, H. L., An introduction to the theory of numbers, 5th edn (Wiley, 1991).Google Scholar
30.Paštéka, M., Some properties of Buck's measure density, Math. Slovaca 42(1) (1992), 15–32.Google Scholar
31.Paštéka, M. and Šalát, T., Buck's measure density and sets of positive integers containing arithmetic progression, Math. Slovaca 41(3) (1991), 283–293.Google Scholar
32.Pincus, D., The strength of the Hahn-Banach theorem, in Victoria symposium on nonstandard analysis, Lecture Notes in Mathematics (eds Hurd, A. E. and Loeb, P.), Volume 369, pp. 203–248 (Springer, Berlin, 1974).CrossRefGoogle Scholar
33.Pólya, G., Untersuchungen über Lücken und Singularitäten von Potenzreihen, Math. Zeit., 29 (1929), 549–640.CrossRefGoogle Scholar
34.Roth, K. F., Sur quelques ensembles d'entiers, C. R. Acad. Sci. Paris 234 (1952), 388–390.Google Scholar
35.Roth, K. F., On certain sets of integers, J. Lond. Math. Soc. 28 (1953), 104–109.CrossRefGoogle Scholar
36.Šalát, T. and Tijdeman, R., Asymptotic densities of sets of positive integers, Math. Slovaca, 33(2) (1983), 199–207.Google Scholar
37.Schechter, E., Handbook of analysis and its foundations (Academic Press, 1996).Google Scholar
38.Sierpiński, W., Elementary theory of numbers, 2nd edn, North-Holland Mathematical Library, Volume 31 (North-Holland, Amsterdam, 1988).Google Scholar
39.Sleziak, M. and Ziman, M., Lévy group and density measures, J. Number Theory 128(12) (2008), 3005–3012.CrossRefGoogle Scholar
40.Soifer, A., The mathematical coloring book (Springer-Verlag, New York, 2009).CrossRefGoogle Scholar
41.Szemerédi, E., On sets of integers containing no k elements in arithmetic progression, Acta Arith. 27 (1975), 199–245.CrossRefGoogle Scholar
42.Tenenbaum, G., Introduction to analytic and probabilistic number theory, Cambridge Studies in Advanced Mathematics, Volume 46 (Cambridge University Press, Cambridge, 1995).Google Scholar
43.van Douwen, E. K., Finitely additive measures on ℕ, Topology Appl. 47(3) (1992), 223–268.CrossRefGoogle Scholar