No CrossRef data available.
Article contents
A Note on the Fundamental Group of Kodaira Fibrations
Published online by Cambridge University Press: 30 January 2019
Abstract
The fundamental group π of a Kodaira fibration is, by definition, the extension of a surface group 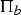 $\Pi_b$ by another surface group
$\Pi_b$ by another surface group 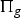 $\Pi _g$, i.e.
$\Pi _g$, i.e.
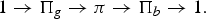 $$1 \rightarrow \Pi_g \rightarrow \pi \rightarrow \Pi_b \rightarrow 1.$$
$$1 \rightarrow \Pi_g \rightarrow \pi \rightarrow \Pi_b \rightarrow 1.$$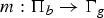 $m \colon \Pi_b \to \Gamma_g$ in terms of the coinvariant homology of
$m \colon \Pi_b \to \Gamma_g$ in terms of the coinvariant homology of 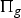 $\Pi_g$. In particular, we observe that if π is the fundamental group of a Kodaira fibration with relative irregularity g−s, then
$\Pi_g$. In particular, we observe that if π is the fundamental group of a Kodaira fibration with relative irregularity g−s, then 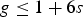 $g \leq 1+ 6s$, and we show that this effectively constrains the possible choices for π, namely that there are group extensions as above that fail to satisfy this bound, hence it cannot be the fundamental group of a Kodaira fibration. A noteworthy consequence of this construction is that it provides examples of symplectic 4-manifolds that fail to admit a Kähler structure for reasons that eschew the usual obstructions.
$g \leq 1+ 6s$, and we show that this effectively constrains the possible choices for π, namely that there are group extensions as above that fail to satisfy this bound, hence it cannot be the fundamental group of a Kodaira fibration. A noteworthy consequence of this construction is that it provides examples of symplectic 4-manifolds that fail to admit a Kähler structure for reasons that eschew the usual obstructions.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 62 , Issue 3 , August 2019 , pp. 739 - 746
- Copyright
- Copyright © Edinburgh Mathematical Society 2019


