Hostname: page-component-77c89778f8-7drxs Total loading time: 0 Render date: 2024-07-17T13:59:57.571Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence and Concentration of Positive Solutions for Nonlinear Kirchhoff-Type Problems with a General Critical Nonlinearity

Part of: Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  17 July 2018

Jianjun Zhang ,
David G. Costa  and
João Marcos do Ó
Jianjun Zhang
Affiliation:
College of Mathematics and Statistics, Chongqing Jiaotong University, Chongqing 400074, PR China (zhangjianjun09@tsinghua.org.cn) Dip. di Scienza e Alta Tecnologia, Università degli Studi dell'Insubria, via Valleggio 11, 22100 Como, Italy
David G. Costa
Affiliation:
Department of Mathematical Sciences, University of Nevada, Las Vegas, PO Box 454020 NV, USA (costa@unlv.nevada.edu)
João Marcos do Ó
Affiliation:
Department of Mathematics, Federal University of Paraíba, 58051-900 João Pessoa-PB, Brazil (jmbo@pq.cnpq.br)
Get access Rights & Permissions [Opens in a new window]

Abstract

We are concerned with the following Kirchhoff-type equation

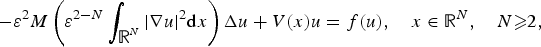$$ - \varepsilon ^2M\left( {\varepsilon ^{2 - N}\int_{{\open R}^N} {\vert \nabla u \vert^2{\rm d}x} } \right)\Delta u + V(x)u = f(u),\quad x \in {{\open R}^N},\quad N{\rm \ges }2,$$
where M ∈ C(ℝ+, ℝ+), V ∈ C(ℝN, ℝ+) and f(s) is of critical growth. In this paper, we construct a localized bound state solution concentrating at a local minimum of V as ε → 0 under certain conditions on f(s), M and V. In particular, the monotonicity of f(s)/s and the Ambrosetti–Rabinowitz condition are not required.

Keywords

Kirchhoff equationsexistence and concentrationcritical growth

MSC classification

Primary: 35B25: Singular perturbations
Secondary: 35B33: Critical exponents 35J61: Semilinear elliptic equations
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 61 , Issue 4 , November 2018 , pp. 1023 - 1040
Copyright
Copyright © Edinburgh Mathematical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Adimurthi, Existence of positive solutions of the semilinear Dirichlet problem with critical growth for the n-Laplacian, Ann. Sc. Norm. Super. Pisa Cl. Sci. 17 (1990), 393–413.Google Scholar
2Alves, C. O., Souto, M. A. S. and Montenegro, M., Existence of a ground state solution for a nonlinear scalar field equation with critical growth. Calc. Var. Partial Differential Equations 43 (2012), 537–554.Google Scholar
3Ambrosetti, A. and Wang, Z. Q., Nonlinear Schröinger equations with vanishing and decaying potentials, Differential Integral Equations 18 (2005), 1321–1332.Google Scholar
4Azzollini, A., A note on the elliptic Kirchhoff equation in ℝN perturbed by a local nonlinearity, Commun. Contem. Math. 17 (2015), 1450039.Google Scholar
5Berestycki, H., Gallouët, T. and Kavian, O., Equations de champs scalaires euclidens non linéires dans le plan, C. R. Acad. Sc. Paris Série I-Math. 297 (1983), 307–310 and Publications du Laboratoire d'Analyse Numérique, Université de Paris VI (1984).Google Scholar
6Berestycki, H. and Lions, P. L., Nonlinear scalar field equations I. Existence of a ground state, Arch. Ration. Mech. Anal. 82 (1983), 313–346.Google Scholar
7Byeon, J. and Jeanjean, L., Standing waves for nonlinear Schrödinger equations with a general nonlinearity, Arch. Ration. Mech. Anal. 185 (2007), 185–200.Google Scholar
8Byeon, J., Jeanjean, L. and Maris, M., Symmetric and monotonicity of least energy solutions, Calc. Var. Partial Differential Equations 36 (2009), 481–492.Google Scholar
9Byeon, J., Jeanjean, L. and Tanaka, K., Standing waves for nonlinear Schrödinger equations with a general nonlinearity: one and two dimensional case, Comm. Partial Differential Equations 33 (2008), 1113–1136.Google Scholar
10Byeon, J. and Wang, Z.-Q., Standing waves with a critical frequency for nonlinear Schrödinger equations, Arch. Ration. Mech. Anal. 65 (2002), 295–316.Google Scholar
11Byeon, J., Zhang, J. J. and Zou, W. M., Singularly perturbed nonlinear Dirichlet problems involving critical growth, Calc. Var. Partial Differential Equations 47 (2013), 65–85.Google Scholar
12Cao, D. and Noussair, E. S., Multi-bump standing waves with a critical frequency for nonlinear Schrödinger equations, J. Differential Equations 203 (2004), 292–312.Google Scholar
13Cao, D., Noussair, E. S. and Yan, S., Multiscale-bump standing waves with a critical frequency for nonlinear Schrödinger equations, Trans. Amer. Math. Soc. 360 (2008), 3813–3837.Google Scholar
14Cao, D. and Yan, S., Multi-bump bound states of Schrödinger equations with a critical frequency, Math. Ann. 336 (2006), 925–948.Google Scholar
15de Figueiredo, D. G., Miyagaki, O. H. and Ruf, B., Elliptic equations in ℝ2 with nonlinearities in the critical growth range, Calc. Var. Partial Differential Equations 3 (1995), 139–153.Google Scholar
16del Pino, M. and Felmer, P., Local mountain passes for semilinear elliptic problems in unbounded domains, Calc. Var. Partial Differential Equations 4 (1996), 121–137.Google Scholar
17do Ó, J. M., N-Laplacian equations in ℝN with critical growth, Abstr. Appl. Anal. 2 (1997), 301–315.Google Scholar
18do Ó, J. M., Sani, F. and Zhang, J. J., Stationary nonlinear Schrödinger equations in ℝ2 with potentials vanishing at infinity, Ann. Mat. Pura Appl. 196 (2017), 363–393.Google Scholar
19do Ó, J. M. and Souto, M. A. S., On a class of nonlinear Schrödinger equations in ℝ2 involving critical grwoth, J. Differential Equations 174 (2001), 289–311.Google Scholar
20Evans, L. C., Partial differential equations, Graduate Studies in Mathematics, Volume 19 (American Mathematical Society, Providence, RI, 1998).Google Scholar
21Figueiredo, G. M., Ikoma, N. and Júnior, J. R. S., Existence and concentration result for the Kirchhoff equations with general nonlinearities, Arch. Ration. Mech. Anal. 213 (2014), 931–979.Google Scholar
22Floer, A. and Weinstein, A., Nonspreading wave packets for the cubic Schrödinger equations with a bounded potential, J. Funct. Anal. 69 (1986), 397–408.Google Scholar
23He, Y., Concentrating bounded states for a class of singularly perturbed Kirchhoff type equations with a general nonlinearity, J. Differential Equations 261 (2016), 6178–6220.Google Scholar
24He, Y. and Li, G., Standing waves for a class of Kirchhoff type problems in ℝ3 involving critical Sobolev exponents, Calc. Var. Partial Differential Equations 54 (2015), 3067–3106.Google Scholar
25He, X. and Zou, W., Existence and concentration behavior of positive solutions for a Kirchhoff equation in ℝ3, J. Differential Equations 2 (2012), 1813–1834.Google Scholar
26Jeanjean, L. and Tanaka, K., A remark on least energy solution in ℝN, Proc. Amer. Math. Soc. 13 (2002), 2399–2408.Google Scholar
27Jost, J., Partial differential equations (Springer-Verlag, New York, 2002).Google Scholar
28Kirchhoff, G., Mechanik (Teubner, Leipzig, 1883).Google Scholar
29Lions, J.-L., On some questions in boundary value problems of mathematical physics, in: Contemporary developments in continuum mechanics and partial differential equations (eds de la Penha, G. and Medeiros, L. A. J.) (Proceedings of the International Symposium on Continuum Mechanics and Partial Differential Equations Rio de Janeiro, 1977), North-Holland Mathematic Studies, Volume 30, pp. 284–346 (North-Holland, Amsterdam–New York, 1978).Google Scholar
30Moroz, V. and Schaftingen, J. V., Semiclassical stationary states for nonlinear Schrödinger equations with fast decaying potentials. Calc. Var. Partial Differential Equations 37 (2010), 1–27.Google Scholar
31Oh, Y. G., Existence of semiclassical bound states of nonlinear Schrödinger equations with potentials of the class (V)a, Comm. Partial Differential Equations 13 (1988), 1499–1519.Google Scholar
32Rabinowitz, P. H., On a class of nonlinear Schrödinger equations, Z. Angew. Math. Phys. 43 (1992), 270–291.Google Scholar
33Ruf, B. and Sani, F., Ground states for elliptic equations in ℝ2 with exponential critical growth, In Geometric Properties for Parabolic and Elliptic PDEs (eds Magnanini, R., Sakaguchi, S. and Alvino, A.), Springer INdAM Series, Volume 2, pp. 251–267 (Springer, Milan, 2013).Google Scholar
34Strauss, W. A., Existence of solitary waves in higher dimensions, Commun. Math. Phys. 55 (1997), 149–162.Google Scholar
35Wang, X., On concentration of positive bound states of nonlinear Schrödinger equations, Commun. Math. Phys. 153 (1993), 229–244.Google Scholar
36Wang, J., Tian, L., Xu, J. and Zhang, F., Multiplicity and concentration of positive solutions for a Kirchhoff type problem with critical growth, J. Differential Equations 253 (2012), 2314–2351.Google Scholar
37Zhang, J., Chen, Z. and Zou, W., Standing waves for nonlinear Schrödinger equations involving critical growth, J. Lond. Math. Soc. 90 (2014), 827–844.Google Scholar
38Zhang, J. J. and do Ó, J. M., Standing waves for nonlinear Schrödinger equations involving critical growth of Trudinger-Moser type, Z. Angew. Math. Phys. 66 (2015), 3049–3060.Google Scholar
39Zhang, J. J. and Zou, W. M., A Berestycki-Lions theorem revisited, Commun. Contem. Math. 14 (2012), 1250033.Google Scholar