Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
GONÇALVES, JAIRO Z.
and
DEL RÍO, ÁNGEL
2013.
A SURVEY ON FREE SUBGROUPS IN THE GROUP OF UNITS OF GROUP RINGS.
Journal of Algebra and Its Applications,
Vol. 12,
Issue. 06,
p.
1350004.


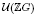 , the group of units of ℤ
, the group of units of ℤ