Article contents
A SPECTRUM OF SERIES–PARALLEL GRAPHS WITH MULTIPLE EDGE EVOLUTION
Published online by Cambridge University Press: 26 January 2019
Abstract
We discuss a rich family of directed series–parallel (SP) graphs grown by the simultaneous random series or parallel development of multiple edges. The family portrays a spectrum that spans a wide range of SP graphs: from simple models, where only as few as one edge is chosen for evolution at each discrete point in time, to complex hierarchical lattice networks grown by a take-all strategy, where all the edges in the existing network are developed.
The family of SP graphs we discuss is grown from an initial seed graph with τ0 edges under an arbitrary building sequence, 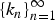 $\{k_{n}\}_{n=1}^{\infty}$, of nonnegative integers (with
$\{k_{n}\}_{n=1}^{\infty}$, of nonnegative integers (with 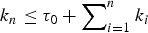 $k_n \le \tau _0 + \sum\nolimits_{i = 1}^n {k_i} $, for arbitrary τ0 ≥ 1), that specifies the number of edges subjected to evolution at time n. We study the average north polar degree and show that we can go beyond averages to strong laws. We also find the exact average number of critical edges. The asymptotics of the critical edges are facilitated under the regularity condition that
$k_n \le \tau _0 + \sum\nolimits_{i = 1}^n {k_i} $, for arbitrary τ0 ≥ 1), that specifies the number of edges subjected to evolution at time n. We study the average north polar degree and show that we can go beyond averages to strong laws. We also find the exact average number of critical edges. The asymptotics of the critical edges are facilitated under the regularity condition that 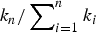 $k_n/\sum\nolimits_{i = 1}^n {k_i} $ converges to a constant (as n → ∞), a natural condition easily met by practical strategies, such as single-edge evolution and take-all choice, and much in between.
$k_n/\sum\nolimits_{i = 1}^n {k_i} $ converges to a constant (as n → ∞), a natural condition easily met by practical strategies, such as single-edge evolution and take-all choice, and much in between.
MSC classification
- Type
- Research Article
- Information
- Probability in the Engineering and Informational Sciences , Volume 33 , Issue 4 , October 2019 , pp. 487 - 499
- Copyright
- Copyright © Cambridge University Press 2019
References
- 3
- Cited by


