 $GI/GI/K$ QUEUE GIVEN PARTIAL INFORMATION
$GI/GI/K$ QUEUE GIVEN PARTIAL INFORMATIONPublished online by Cambridge University Press: 25 September 2020
In order to understand queueing performance given only partial information about the model, we propose determining intervals of likely values of performance measures given that limited information. We illustrate this approach for the mean steady-state waiting time in the 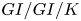 $GI/GI/K$ queue. We start by specifying the first two moments of the interarrival-time and service-time distributions, and then consider additional information about these underlying distributions, in particular, a third moment and a Laplace transform value. As a theoretical basis, we apply extremal models yielding tight upper and lower bounds on the asymptotic decay rate of the steady-state waiting-time tail probability. We illustrate by constructing the theoretically justified intervals of values for the decay rate and the associated heuristically determined interval of values for the mean waiting times. Without extra information, the extremal models involve two-point distributions, which yield a wide range for the mean. Adding constraints on the third moment and a transform value produces three-point extremal distributions, which significantly reduce the range, producing practical levels of accuracy.
$GI/GI/K$ queue. We start by specifying the first two moments of the interarrival-time and service-time distributions, and then consider additional information about these underlying distributions, in particular, a third moment and a Laplace transform value. As a theoretical basis, we apply extremal models yielding tight upper and lower bounds on the asymptotic decay rate of the steady-state waiting-time tail probability. We illustrate by constructing the theoretically justified intervals of values for the decay rate and the associated heuristically determined interval of values for the mean waiting times. Without extra information, the extremal models involve two-point distributions, which yield a wide range for the mean. Adding constraints on the third moment and a transform value produces three-point extremal distributions, which significantly reduce the range, producing practical levels of accuracy.