Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-19T11:07:37.363Z Has data issue: false hasContentIssue false
  • English
  • Français

On Optimal Permutation Scheduling in Stochastic Proportionate Flowshops

Published online by Cambridge University Press:  27 July 2009

Michael Pinedo ,
Dequan Shaw  and
Xiuli Chao
Michael Pinedo
Affiliation:
Department of Industrial Engineering and Operations Research Columbia University, New York, New York 10027
Dequan Shaw
Affiliation:
Department of Industrial Engineering and Operations Research Columbia University, New York, New York 10027
Xiuli Chao
Affiliation:
Division of Industrial and Management Engineering New Jersey Institute of Technology, Newark, New Jersey 07102
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider m machines in series with unlimited intermediate buffers and n jobs available at time zero. The processing times of job j on all m machines are equal to a random variable Xj with distribution Fj. Various cost functions are analyzed using stochastic order relationships. First, we focus on minimizing 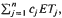where cj is the weight (holding cost) and Tj the completion time of job j. We establish that if 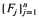are in a class of distributions we define as SIFR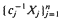, and and 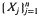are increasing sequences of likelihood ratio-ordered and stochastic-ordered random variables, respectively, the job sequence [1, 2, … n ] is optimal among all static permutation schedules. Second, for arbitrary processing time distributions, if 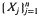is an increasing sequence of likelihood ratio-ordered (hazard rate-ordered) random variables and the costs 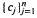are nonincreasing, then a general cost function is minimized by the job sequence [1,2,…, n] in the stochastic ordering (increasing convex ordering) sense.

Type
Articles
Information
Probability in the Engineering and Informational Sciences , Volume 6 , Issue 4 , October 1992 , pp. 513 - 523
Copyright
Copyright © Cambridge University Press 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barlow, R.E. & Proschan, F. (1981). Statistical theory of reliability and life testing probability models. Silver Spring, MD: To Begin With.Google Scholar
Brown, M. & Solomon, H. (1973). Optimal issuing policies under stochastic field lives. Journal of Applied Probability 10(4):761–768.CrossRefGoogle Scholar
Chang, C.S., Chao, X., Pinedo, M., & Weber, R. (1992). On the optimality of the LEPT rule and cμ rule for machines in parallel. Journal of Applied Probability (to appear).CrossRefGoogle Scholar
Chang, C.S. & Yao, D.D. (1990). Rearrangement, majorization and stochastic scheduling. International Business Machines, Report 16250.Google Scholar
Forst, F.G. (1983). Minimizing total expected cost in the two-machine, stochastic flow shop. O.R. Letters 2(2, 06), pp. 58–61.CrossRefGoogle Scholar
Ow, P.S. (1985). Focused scheduling in proportionate flowshops. Management Science 31(7, 07), pp. 852–869.CrossRefGoogle Scholar
Pinedo, M. & Wie, S.H. (1986). Inequalities for stochastic flow shops and job shops. Applied Stochastic Models and Data Analysis 2: 61–69.CrossRefGoogle Scholar
Pinedo, M. (1985). A note on stochastic shop models in which jobs have the same processing requirement on each machine. Management Science 31 (7, 07), pp. 840–846.CrossRefGoogle Scholar
Pinedo, M.L. & Rammouz, E. (1988). A note on stochastic scheduling on a single machine subject to breakdown and repair. Probability in the Engineering and Informational Sciences 2: 41–49.CrossRefGoogle Scholar
Ross, S.M. (1983). Stochastic processes. New York: Wiley & Sons.Google Scholar
Shanthikumar, J.G. & Yao, D.D. (1991). Bivariate characterization of some stochastic order relations. Advances in Applied Probability 23: 642–659.CrossRefGoogle Scholar
Stoyan, D. (1983). Comparison methods for queues and other stochastic models. New York: Wiley & Sons.Google Scholar