INTRODUCTION
Tropical theileriosis is caused by Theileria annulata, a protozoan parasite transmitted between cattle by ticks of the genus Hyalomma. In many parts of the world T. annulata is considered to be a major threat to the cattle industry (Norval et al. Reference Norval, Perry and Young1992; Gharbi et al. Reference Gharbi, Sassi, Dorchies and Darghouth2006). Initial infection with T. annulata typically causes a clinical infection, with risk of substantial morbidity and death. Cattle that survive the acute stage become carriers, with the possibility of then being continually infected and infectious for several years (Norval et al. Reference Norval, Perry and Young1992). Gharbi et al. (Reference Gharbi, Sassi, Dorchies and Darghouth2006) have demonstrated that the carrier state imposes a considerable burden on cattle productivity, including weight loss, reduced milk production and anaemia.
Hyalomma ticks develop from eggs into larvae, nymphae and adults with a moult required between each stage. They generally behave as ‘two-host’ ticks, i.e. they attach to a host as larva, and then feed and moult and feed again on the same host before detaching as nymphs, moulting to adults, and seeking a host on which to feed for the final time and mate. Females then detach and lay eggs. However, there is also evidence that Hyalomma ticks may behave as ‘three-host’ ticks taking a different host at larvae, nymph and adult stages with all moulting taking place off host (Chaudhuri et al. Reference Chaudhuri, Srivastava and Naithani1969; Alahmed and Kheir, Reference Alahmed and Kheir2003). Tick physiology and hence population dynamics are highly dependent on environmental conditions (especially temperature and moisture) for development and survival. Although they are able to regulate their survival by finding suitable microhabitats during moulting, when questing for hosts they are forced to become more exposed. Consequently, in seasonal climates, questing ticks are only active during periods in which the temperature range and humidity are suitable. In particular, the numbers of questing (and therefore attached) ticks drops dramatically during colder months, and during hot, dry periods. Typically, around the Mediterranean, this seasonality results in a segregation of the tick stages into different periods, with questing adults appearing during the spring, and then eggs, larvae, nymphae appearing sequentially throughout the summer.
There have been no previous studies that have considered the transmission dynamics of T. annulata. However, the epidemiology of East Coast fever caused by the related T. parva has been investigated through the use of mathematical models that have focused on the life cycle of its vector Rhipicephalus appendiculatus (King et al. Reference King, Gettinby and Newson1988), the host and parasite (Gettinby and Byrom, Reference Gettinby and Byrom1989) and the transmission dynamics of T. parva in eastern Africa (Medley et al. Reference Medley, Perry and Young1993), although this last study did not explicitly describe the tick population since it was designed for a non-seasonal, equatorial context (i.e. the tick attachment rate can be assumed constant). However, T. annulata is found extensively outside of equatorial regions, and so the tick population can be highly seasonal, and the tick attachment rate varies accordingly.
The aim of this study was to gain a greater insight into the transmission dynamics of T. annulata with a view to planning interventions that will reduce the number of clinical and carrier infections in cattle. A greater understanding of the seasonal behaviour of the tick population and its impact on infection within the cattle population will allow the impact of the timing of alternative interventions to be better understood.
The model proposed here describes the dynamics of a tick population including its different stages of development and seasonal variation. From this first step the model is then expanded to a model of T. annulata infection in the host cattle population. An examination of the transmission dynamics of T. annulata is undertaken with an investigation into the impact of alternative intervention measures that target the tick population also being considered.
MATERIALS AND METHODS
This model describing the transmission dynamics of T. annulata consists of 2 host components: the Hyalomma tick and the cattle populations. We describe the structure and parameterization of each component of the model in turn, leading to a single infection transmission model. Parameters are either taken from the literature or fitted by maximum likelihood to unpublished data collected in Turkey during 2006–2008.
Data collected from farms in Turkey included the removal and examination of ticks from infested cattle. Of the Hyalomma ticks collected from cattle, 50% (7360/14541) were the species H. marginatum marginatum, 26% (3717/14541) were H. anatolicum excavatum 20% (2979/14541) were H. detritum detritum and the remainder (485/14541) were unidentified Hyalomma species.
Model structure – Hyalomma tick population
In contrast to previous similar models (e.g. Medley et al. Reference Medley, Perry and Young1993), rather than simply describing the tick population through the use of a single infection parameter that is applied to the cattle population, in this study the tick population is explicitly described. This approach was adopted for 2 reasons: (1) it allowed an examination of the role of the tick population and its impact on the overall transmission dynamics of the system and (2) the impact of interventions that target these tick states can be explicitly examined.
In this study the proposed model describes a generic Hyalomma tick population that does not differentiate between species, the structure of which is shown in Fig. 1. This is a simplified interpretation of the life cycle of the Hyalomma tick population, and, in particular we assume a two-host life cycle. This can be justified given that the majority of Hyalomma ticks found in the data set were H. marginatum marginatum which is a two-host tick. It has been shown that many species of Hyalomma tick are able to transmit T. annulata (Norval et al. Reference Norval, Perry and Young1992). To the authors’ knowledge, the impact of the species of Hyalomma tick on the transmission of T. annulata has not been investigated, therefore in this study all Hyalomma species have been grouped together. The attached immatures (AI) are ticks that appear on the host and combine feeding larvae, engorged larvae and then following on-host moulting feeding nymphae and engorged nymphae. It is during this state as attached immatures that ticks may become infected with T. annulata. Following detachment from the host, ticks hibernate and moult from nymphs into adults and then actively quest for their second host; these stages all occur in the model as the questing adult (QA) state. Feeding adults (FA) are those ticks that are on a host and feeding, it is during this period that an infected tick may transmit infection to the cattle host. The final state is the egg-laying adult state (ELA), this incorporates all other parts of the tick life-cycle including egg-laying females, eggs, hardening larvae (the period before larvae become active which allows the body cuticle and mouthpart to harden), and questing larvae which are actively seeking a host (Snow, Reference Snow1969).

Fig. 1. Model Structure describing the Hyalomma tick population.
The tick model proposed here is a deterministic model described by a system of differential equations (Appendix I). From Fig. 1 each mutually exclusive department represents a different stage of tick development while the arrows represent the flows through the stages: vertical arrows represent development, and all stages are subject to mortality. It has been shown in previous studies that the growth and progression of Hyalomma ticks is seasonal, closely following temperature (Chaudhuri et al. Reference Chaudhuri, Srivastava and Naithani1969; Snow, Reference Snow1969; Alahmed and Kheir, Reference Alahmed and Kheir2003), although for simplicity only seasonal variation in the rate that ticks become attached immatures (i.e. host seeking of larvae) is considered here (through the use of a cosine function), with remaining parameters being maintained at a constant value throughout the year. While it is acknowledged that additional seasonality could be introduced for other parameters this has not been done as the main focus of the model is considering T. annulata infection within the cattle population. Additionally, there is insufficient detailed, quantitative data available to model the biological processes mechanistically. The empirical process used in the model would have to be adapted to data or patterns from other locales to apply the model to different environment conditions. To prevent the tick population growing exponentially, a density-dependent rate at which attached immatures die is incorporated into the model. To ensure that questing adults (QA) spend a pre-defined length of time in this stage (which includes hibernation and moulting from nymphae), this has been modelled as a sequence of 6 shorter stages with constant rates of transfer between each, generating a gamma-distributed sojourn in the whole stage, with shape parameter 6 and rate parameter, ζ. Consequently, the mean sojourn in this stage is given as ζ/6 with variance ζ/6 (Keeling and Rohani, Reference Keeling and Rohani2007).
Parameterization – Hyalomma tick model
To parameterize this model it is necessary to obtain parameter values from a number of different sources. Where possible parameters were obtained from secondary data sources; however, in many cases these data sources provided information from laboratory conditions (Chaudhuri et al. Reference Chaudhuri, Srivastava and Naithani1969; Snow, Reference Snow1969; Sardey and Ghafoor, Reference Sardey and Ghafoor1971; Ghosh and Azhahianambi, Reference Ghosh and Azhahianambi2007) rather than the field. Parameters for which estimates could not be gained from the literature were estimated from the current data (Table 1).
Table 1. Parameter values used for tick component of the transmission model

Data collected from farms in Turkey from 2006 to 2008 that describe the number of attached Hyalomma nymphae and adult ticks collected from cattle were used to parameterize the Hyalomma tick model. Figures 2 and 3 show the average numbers of nymphs and adults collected from cattle during this period along with the model fit to data shown in Fig. 3. From Fig. 2, the majority of animals had very few ticks if any with the counts of ticks on the natural hosts being overdispersed (Petney et al. Reference Petney, van Ark and Spickett1990) and therefore for the purpose of obtaining the likelihood function it has been assumed here that the individual counts were distributed as a negative binomial distribution. To account for potential discrepancies between reported numbers of immature and adult ticks (reduced numbers of immature ticks found during data collection), a correction factor (ρ) was introduced into the model that was estimated during the process of obtaining the model fit to the Hyalomma data (Fig. 3) using maximum likelihood described in Appendix II. There are several competing processes controlling the value of this factor. First, immature ticks are considerably harder to count (they are smaller and do not congregate to specific anatomical areas). Second, immature ticks may feed on smaller, non-bovine hosts (Norval et al. Reference Norval, Perry and Young1992). Third, immature and adult ticks will have different residence times on the host, so that a count of the standing infestation will not be a direct measure of the population size. The value for the correction factor was found to be 53·6 indicating that there are 53·6 times more immature ticks in the system than were actually found during the data collection exercise. This value would appear credible particularly when considering that no larvae were found during data collection, while in a previous study that considered Rhipicephalus appendiculatus for under-reporting purposes the number of larvae reported was multiplied by 100 and for nymphs these were multiplied by 10 (Randolph, Reference Randolph1997).

Fig. 2. The frequency of nymph and adult Hyalomma counts on cattle that were examined in Turkey from 2006 to 2008.

Fig. 3. Average number of Hyalomma nymphae and adult ticks found on cattle in Turkey during 2006–2008, and the model fit to data for immature and adult ticks respectively. (In all but one case the model is within the 95% confidence intervals of the data points, which are not shown due to their size.)
The majority of immature ticks appear on cattle during October–November while the adult ticks generally appear on cattle around March–July. Further studies show similar patterns of seasonality (Bouattour et al. Reference Bouattour, Darghouth and Daoud1999; Sayin et al. Reference Sayin, Dincer, Karaer, Cakmak, Inci, Yukari, Eren, Vatansever and Nalbantoglu2003). The model fittings incorporating the maximum likelihood methods are fully described in Appendix II (Hilborn and Mangel, Reference Hilborn and Mangel1997).
Cattle model parameterization
The model describing cattle population and T. annulata infection is shown in Fig. 4, and parameter values given in Table 2. The model equations and the maximum likelihood techniques used to estimate unknown parameters are described in Appendix II.

Fig. 4. Model structure describing the natural history of Theileria annulata infection in the cattle population stratified by age.
Table 2. Cattle model parameters

Calves are born into the susceptible state of the cattle population. Although previous studies have suggested the presence of colostral antibodies that provide immunity for calves during their first 3 months (Gharbi et al. Reference Gharbi, Sassi, Dorchies and Darghouth2006), evidence of this was not found in the infection data (see below), and so was not incorporated in the model. Animals in the susceptible state may become infected by T. annulata and if so move to the incubating infection state. From the incubating state an animal may either become clinically infected or move straight into the carrier state, the probability of this being variable and dependent on age (κ(a)). Cattle that survive initial infection become carriers, and remain in that state until death. In this study the definition of the carrier state is the ability of an infected and recovered host to infect ticks, which are then able to transmit the parasite to susceptible animals (Norval et al. Reference Norval, Perry and Young1992).
A previous study investigating T. annulata in Tunisia (Darghouth et al. Reference Darghouth, Bouattour, Ben, Kilani and Brown1996), found that the risk of disease was age dependent, with older aged animals more likely to become clinically infected at first exposure to T. annulata infection. It was found that the proportion of infections that lead to clinical infection was 12·6% in cattle exposed to 3 or more disease seasons in an area of endemic instability (evidence of past infection <100% in cattle exposed to 4 theileriosis seasons or more) which is a similar situation to that described by the Turkish data (see below). This estimate will increase with age (Norval et al. Reference Norval, Perry and Young1992). For this reason the function κ(a)=1–e−0·0233a has been used here, representing the increased likelihood of clinical infection at older ages. This function was obtained by assuming that there will be 12·6% of infections resulting in clinical infection at 6 years of age.
Cattle ageing was implemented by realistic age structuring (Schenzle, Reference Schenzle1984) as follows: calves enter the model into the first age cohort (0 years of age) constantly through time; thereafter cattle change age cohorts at the beginning of each calendar year with all cattle being maintained in 1 year cohorts and moved up to the next cohort. Fifty % of cattle are culled on their 1st birthday and then cattle die at a constant rate (0·1987 yr−1) implemented at each year-end with any remaining cattle dying on their 9th birthday. This is implemented in agreement with the age distribution of cattle in Turkey (data not shown). The gender of the cattle is not explicitly modelled: instead it is assumed that 90% of the cattle are female, again in agreement with the Turkish data (data not shown). The birth rate is dependent on the estimated number of female cattle in the population, and is set so that the number of cattle in the herd is kept at a constant value Ω (in this case 1, so that the model can provide an output as proportions).
Infection dynamics
In order to model the flow of T. annulata in the tick and cattle populations, attached immatures, questing adults, and feeding adults are stratified as either susceptible or infected. It has been assumed here that the infection does not have any impact on the behavioural or demographical characteristics of the ticks and consequently this does not have any impact on the previously calculated parameter values for the tick model. Infection in the cattle population is due to infected adult ticks attaching to susceptible cattle, while ticks themselves may become infected as immature ticks when they come into contact with infectious cattle. This approach is based on that described in previous studies (Medley et al. Reference Medley, Perry and Young1993; O'Callaghan et al. Reference O'Callaghan, Medley, Peter and Perry1998), and is modelled through a system of deterministic equations (see Appendix I). Further assumptions related to the infection dynamics of T. annulata that are applied in this study are as follows (1) ticks will attach to infected and susceptible cattle with equal likelihood. (2) Ticks are infected homogeneously; that is, the variation in the level of infectivity between infected ticks is not considered. (3) The period of clinical infection in cattle is the same irrespective of outcome (survival or death).
Infection parameters – parameterization
The infection status of cattle was assessed in the same study as the tick counts. Blood samples were subject to both an immunofluorescence antibody test (IFAT) and a reverse line blot (RLB) test. The tests were implemented between May and September from 2006 to 2008 starting in June 2006 and ending in September 2008. For those samples that received both tests, trends in the prevalence of positive test results did not vary over time either seasonally or annually (not shown). The results of both tests by age are shown in Fig. 5.

Fig. 5. Proportion of cattle test positive by age.
Using the specificity and sensitivity of the RLB (sensitivity=80%, specificity=0·99) and IFAT (Sensitivity=80%, specificity=90%) (Darghouth et al. Reference Darghouth, Sassi, Gharbi, Soudani, Karoui and Krichi2004) an estimate for the true prevalence of infection for the data at each time-point is obtained. The model is then fitted to data using maximum likelihood to obtain estimates for the parameters Cz and π which are the proportion of immature ticks feeding on carrier cattle that become infected, and the probability of infection in cattle due to an attached infected adult tick respectively. The model fit to the data is shown in Fig. 6, with the resulting parameter values shown in Table 2.

Fig. 6. Model fit to infection data, where each panel is an age group showing the estimated prevalence of infection for samples tested for both IFAT and RLB (see text).
In order to obtain estimates of Cz and π, it was necessary to fix the value of Cc, the proportion of ticks that become infected when feeding on clinically infected cattle (=0·1). In the endemic equilibrium state, the majority of cattle are carriers and the period during which cattle are clinically infected is very short. This means that due to the lack of the number of clinically infected cattle and coupled with the short period of infection, it is unlikely that ticks will feed on clinically infected cattle compared to cattle that are carriers, therefore the equilibrium is relatively insensitive to this parameter. However, the impact of this fixed value (Cc) and the other key parameters that describe the transmission of infection between ticks and cattle (Cz, and π) was investigated through sensitivity analysis.
Interventions
Interventions that reduce the tick population are considered. Interventions can either be applied at one time-point, or continuously, and can target either the tick population attached to cattle or in the environment, combining to give 4 basic strategies. In the case of targeting the ticks that are on the cattle, this will represent a situation in which the cattle are sprayed with acaricides, while for the environmental intervention this may represent a similar type of intervention or perhaps the application of rough casting, i.e. plastering of all surfaces with smooth cement to block the cracks and crevices to reduce the size of the ideal environment for the hibernating and questing ticks (Ghosh et al. Reference Ghosh, Azhahianambi and de la Fuente2006).
Four single (one-off) intervention scenarios are described in Table 3. Any intervention that targets ticks of a specific status will affect all the ticks that are in the same location (environment or cattle) and not just those that have been specifically targeted. All ticks in the location are instantaneously reduced by 90%, and then the death rate for these ticks set to 5/tick/day for 30 days following the intervention, before reverting back to their previous levels.
Table 3. Summary of the single (one-off) hypothetical interventions investigated here

The continuous interventions are modelled by increasing the death rates for the whole period of the simulation. Four continuous interventions were investigated for each of the tick population states. As with the one-off interventions the intervention was assumed to be implemented when the targeted tick state was at its maximum size (see timing in Table 3). For each of the interventions the death rate of the targeted tick state was permanently increased to 5/tick/day. Again all these interventions were assumed to have been implemented in 2010.
RESULTS
Transmission dynamics
Figure 7 shows the model output describing the number of feeding adult ticks and the number of clinical infections in cattle. It can be seen that a peak in the number of clinical cases immediately follows the peak in the number of feeding adult ticks, as has been observed in field studies (Flach et al. Reference Flach, Ouhelli, Waddington, Oudich and Spooner1995).

Fig. 7. Model output showing the average number of attached immatures (AI) and feeding adults (FA) (left axis) and the proportion of clinical infections (right axis) in cattle from 2005 to 2007.
Sensitivity analysis
The impact of the key parameters that describe the transmission of infection between ticks and cattle (Cc, Cz, and π) was investigated by running the model to steady state and then introducing 1 infected feeding adult tick into the system in August (the peak time for FA ticks), and then monitoring the number of clinical infections over a 5-year period. Parameter Cc had no impact on the model results and so the results are not shown; however, the results showing the impact of variations in Cz and π are shown in Fig. 8.

Fig. 8. The impact of varying parameters Cz and π on the estimated number of clinical infections, following the introduction of an infected feeding adult tick in August 2010 into a system in which the cattle population is completely susceptible. (Figure for π truncated to 3 years.)
Varying Cz (the proportion of immature ticks feeding on carrier animals that become infected) has no impact on the initial epidemic peak of clinical infections, although the impact is seen in the peaks of clinical infections in future years. In contrast, variations in π (probability of infection due to an adult tick) have a large impact on the first peak of clinical infections after infection is introduced, but less subsequently.
Interventions
The results here describe the impact of a range of interventions that target the tick population on both the tick population and infection within the cattle population. In all cases the model initial conditions are: X(0)=1, AI=100, and FAi=1, with all other population states set to zero. The model was then run to steady state prior to the implementation of the interventions.
As the carrier status of cattle may be a proxy for the negative impact of theileriosis on the cattle population (see Introduction section), it is therefore of interest to investigate the impact of the interventions proposed here on the carrier status of the cattle.
Unsurprisingly, continuous interventions have a greater long-term impact on the carrier prevalence in cattle compared to the single interventions (Fig. 9). It is noted that the time-period required for the loss of carriers is of the order of 9 years which in this model is the maximum lifespan of the definitive host. In contrast, the single interventions targeting ticks on the host have a very limited impact on carrier prevalence. Single interventions targeting ticks off host (QA and ELA), results in a significant reduction in the carrier prevalence, followed by a slow rise.

Fig. 9. The impact of the intervention measures that target respectively: QA questing adults, ELA egg-laying adults, FA feeding adults, AI attached immatures at their seasonal peaks on the carrier prevalence.
The impact of the timing of the single interventions can also be seen when comparing the results for each of the single interventions that target the QA and ELA ticks when each of the tick states is at their peak (March and September respectively). This again demonstrates the value of implementing interventions when the QA are at their peak.
Figure 10 shows the impact of the interventions on the average age of cattle clinical infection. This result shows the impact of the interventions on the force of infection which is inversely related to the average age of infection. It can be seen here that once again the single interventions that target ticks on host (FA and AI) seem to have very little impact on infection in the cattle population, while the continuous interventions have a predictably sustained impact. It is interesting to note how the single intervention targeting the QA appears to have the same comparatively strong impact as the continuous QA intervention, whilst as the single intervention targeting the ELA still has a greater impact compared with those that target ticks on the host.

Fig. 10. The impact of the intervention measures on the average age of the cattle at the time of clinical infection: QA questing adults, ELA egg-laying adults, FA feeding adults, AI attached immatures.
It was also found that the impact of these interventions on the average age of the cattle herd was very minor (not shown). This is due to the small proportion of animals in the herd that become clinically infected and subsequently die and the additional assumption made in this model that the carrier status does not have a negative impact on the death rate of the cattle.
It has been shown here that targeting the questing adults appears to maximize the impact on T. annulata with the continuous interventions being more effective than the single interventions. To provide a greater insight into this intervention the impact of the continuous intervention that target questing adults on the proportion of ticks in each tick state is shown in Fig. 11.

Fig. 11. The impact of the continuous intervention targeting the questing adult population on the total tick population stratified by tick state over time.
It can be seen that while the total number of ticks following the intervention decreases, at all times questing adult ticks represent the greatest proportion of the tick population. This helps to provide an insight into why targeting this tick state has the greatest impact on T. annulata infection.
DISCUSSION
We have developed, implemented and parameterized a transmission dynamic model of T. annulata in cattle and Hyalomma ticks. Although parameterized for the Turkish context, the model could be relatively easily adapted to other locales, i.e. seasonal patterns. There are 2 principal conclusions to be drawn from the model.
First, the seasonal tick population has surprisingly very little impact on the transmission dynamics of T. annulata. Because of the temporal separation of infectious and susceptible ticks, virtually all ticks are infected by carrier cattle, so that annual peaks of disease in cattle do not impact on infection in the vector. This can be expected to have evolutionary consequences in that genotypes of T. annulata that are less likely to develop carriage (e.g. through death of the host) will be selected against.
Second, consideration of different interventions has shown the value of targeting questing adult ticks as this appears to have the largest impact on T. annulata infection in the cattle population. The effectiveness of these interventions is likely to be due to the high proportion of QA ticks in the overall tick population.
The results of this study have shown the potential dangers of allowing a completely susceptible cattle population to be exposed to T. annulata infection. As shown in Fig. 8 following the introduction of a single feeding adult tick, there is a single immediate peak in the number of clinical infections within the wider cattle population. Although, following this high peak, peaks in the number of clinical infections are seen in future years during the summer months, these are far smaller than the initial peak.
The approach to modelling the tick population in this study has simplified the natural history of the tick population to include only those tick states that were included in the data from Turkey (AI and FA) and some additional states so that additional intervention measures can be considered. It is unlikely that a more complex model that more accurately describes the tick population will provide further insights into the transmission dynamics of T. annulata as the presence of the further tick states have been implied in this current model. However a further assumption made in this study was that T. annulata infection does not have any impact on the tick population itself. Previous studies have suggested that this may not be the case where T. annulata infection in Hyalomma anatolicum ticks induced in the laboratory was found to cause death and deformity in moulting ticks (Schein and Friedhoff, Reference Schein and Friedhoff1978), while other studies have found that T. annulata can kill its tick vector in the field (Norval et al. Reference Norval, Perry and Young1992; Samish and Rehacek, Reference Samish and Rehacek1999). This adds weight to the finding demonstrating the relative importance of carrier infection in the cattle population on the transmission dynamics of T. annulata, particularly when the increased dose of infection from acutely infected cattle may have an adverse affect on the tick population. However, in future studies this assumption could be relaxed with an investigation into its impact on model results being undertaken.
It is assumed here that the carrier state within the cattle is both life long and that animals in the carrier state are able to infect ticks. This is in line with previous studies that have also adopted the same definition such as Norval et al. (Reference Norval, Perry and Young1992) who defined the carrier state of Theileria as the ability of an infected and recovered host to infect ticks, which are then able to transmit the parasite to susceptible animals. However, as can be seen in Fig. 6, the prevalence data in the upper age groups does not continue to rise with age. This suggests that there may be evidence of recovery from ‘test positivity’ in the older cattle population, or could be selection of carrier animals for sale and slaughter, which would also explain why cattle in the <1 years age group have a distinctly higher prevalence of infection compared to the cattle that are 1 year older. This would certainly explain why the model does not fit to the <1 year carrier prevalence as well as the other age groups. In this model these factors have not been considered although the possibilities of a declining carrier state by age, and the additional culling of infected animals are acknowledged. Future work could investigate the impact of a recovery rate and additional death rates being included in the model, and how these may impact on the prevalence of infection within the tick population, and more importantly their impact on infection in the cattle population.
It has been assumed in this study that infection within the tick population is homogeneous, i.e. each infected tick delivers the same infectious dose of T. annulata. Additionally, it has been assumed here that the tick infestation of cattle is also homogenous. However, previous studies have shown that in the tick population a small number of the infected ticks may be highly infected and therefore able to transmit infection far more readily (Gill et al. Reference Gill, Bhattacharyulu and Kaur1977), while for cattle, the data here have shown that a small proportion of animals have been found to be highly infested with ticks compared to other animals in the herd. As a suggestion for future work, both infected ticks and infested hosts could both be stratified into low and high infection and infestation respectively. However, while an approach like this may be more realistic, in the case of the tick infection, parameterizing such a model to represent the situation in the field accurately may be highly problematic.
The data here have described the number of ticks found on cattle in Turkey during 2006–2008 along with the infection status of the cattle. These data have allowed this model to be parameterized for a field setting rather than having to rely in many cases on data obtained in more unrealistic laboratory settings. No larvae ticks were found during the data collection exercise and it is likely that due to their size there may have been under-reporting of nymph ticks. However, it is also possible that many of the immature ticks may have fed on hosts other than cattle. Previous studies have shown that for many species of tick, it is not uncommon to find immature ticks feeding on smaller mammals or rodents (Norval et al. Reference Norval, Perry and Young1992). Therefore, an alternative approach to that described here might be to describe a second host that immature ticks may feed on, although it has also been suggested in previous studies that wild animals do not play any role in the epidemiology of this disease, with cattle being considered the main reservoir of infection (Pipano, Reference Pipano, Henson and Campbell1977).
An additional assumption that has been implicit in this model is that no T. annulata infection is introduced into the system from outside the cattle and tick populations. This means that it is likely that the results of the interventions described here may be more optimistic than is the case in reality. However, the approach here has shown the value of implementing interventions that target tick state that represents the largest component of the tick population, this being the QA, while the value implementing interventions that have a more permanent effect such as rough casting has also been demonstrated. Even if infection from outside sources is introduced into the model, it is unlikely that these conclusions will differ.
It is acknowledged that the deterministic approach implemented here may not be the most appropriate approach for such small host population sizes as seen at the farms in Turkey. Instead a stochastic model may have been more appropriate as this allows for the random events that are likely to have a large impact on the dynamics of transmission. However, the model here has allowed the seasonal transmission dynamics of T. annulata between the tick and cattle population to be explicitly modelled and it would be a relatively easy task to take the parameter values obtained here and apply them in a stochastic model. Additionally, the model proposed here could be re-parameterized for differing herd sizes should the relevant data become available.
ACKNOWLEDGEMENTS
Additional thanks go to all those individuals who helped to collect data in Turkey and to the farmers in Turkey who were kind enough to participate in this study. Thanks also to Pelham Barton at Birmingham University for additional helpful comments.
FINANCIAL SUPPORT
The research was funded by a Wellcome grant (058933).
APPENDIX I
Tick population model
The differential equations describing the mathematical structure of the tick population are shown below. Although it should be noted that during the initial model fitting stage to obtain the parameters describing the tick population the equations describing QA and FA were not stratified by infection status as shown below
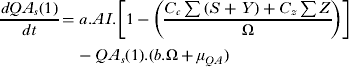



APPENDIX II
Maximum likelihood – tick model
The tick model was fitted to the aggregated tick data using maximum likelihood assuming that tick infestation in the cattle population follows a negative binomial distribution.
Let
p it be data describing the no. of ticks on animal i at month t
q t be the model estimate of the mean tick count at month t
Where w(p it|q t,k) is the negative binomial probability of observing p it ticks given a model estimate of q t and k.
Log-likelihood
The estimated log-likelihood is calculated by summing for all animals and all time points:
One k value (Kn) was adopted for the nymph data while for the adult data there was sufficient variation in the distribution of the ticks over time (not shown) to adopt variable values of k over time. K1 is applied to data from January, February, October, November and December. K2 is applied to data from February to May and K3 is applied to data from June to September.
Maximum likelihood – cattle model
To obtain the infection parameters (see Table 2), the output of the cattle model is fit to count data describing previous infection in cattle over time.
Let
- N at
the number of cattle aged a at time t.
- D at
the number of positive cattle aged a at time t.
- Z at
expected proportion of ever infected (H+Y+S+Z) cattle aged a at time t.
Therefore the log likelihood of the model given the data is: